Chủ đề stp hình trụ: Khám phá STP hình trụ với các công thức tính diện tích và thể tích dễ hiểu. Bài viết cung cấp kiến thức chi tiết, ví dụ minh họa và ứng dụng thực tế. Hãy cùng tìm hiểu để nắm vững cách tính toán và áp dụng vào các bài tập liên quan đến hình trụ.
Mục lục
Công Thức Và Ví Dụ Tính Diện Tích, Thể Tích Hình Trụ
1. Công Thức Tính Diện Tích Hình Trụ
Diện tích xung quanh của hình trụ được tính bằng công thức:
\[ S_{xq} = 2\pi rh \]
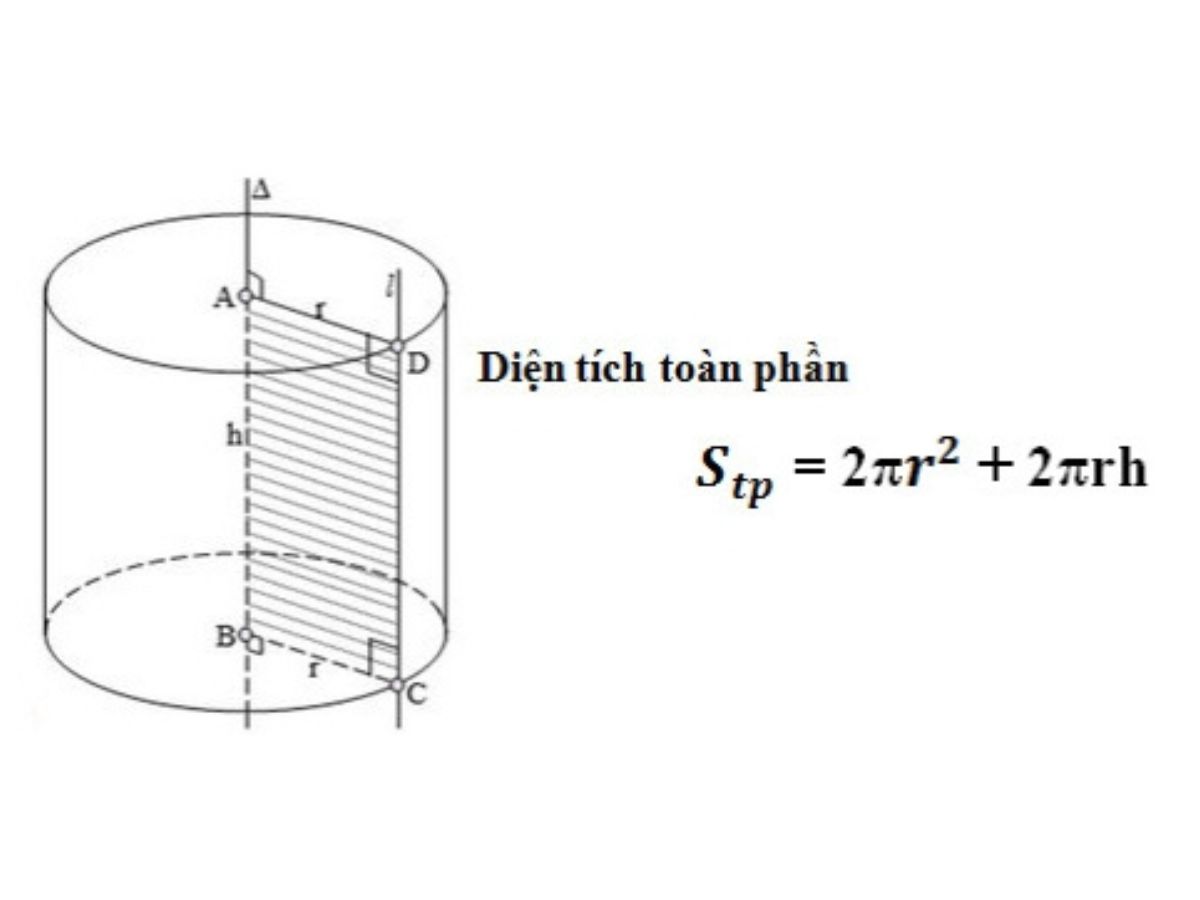
Diện tích toàn phần của hình trụ được tính bằng công thức:
\[ S_{tp} = 2\pi r (r + h) \]
Trong đó:
- \( r \): Bán kính đáy của hình trụ
- \( h \): Chiều cao của hình trụ
2. Ví Dụ Tính Diện Tích Toàn Phần
Ví dụ: Một hình trụ có bán kính đáy \( r = 4 \) cm và chiều cao \( h = 8 \) cm. Tính diện tích toàn phần của hình trụ này.
Lời giải:
Áp dụng công thức:
\[ S_{tp} = 2\pi r (r + h) = 2\pi \cdot 4 \cdot (4 + 8) = 96\pi \, \text{cm}^2 \]
3. Công Thức Tính Thể Tích Hình Trụ
Thể tích của hình trụ được tính bằng công thức:
\[ V = \pi r^2 h \]
4. Ví Dụ Tính Thể Tích
Ví dụ: Cho một hình trụ có bán kính đáy \( r = 3 \) cm và chiều cao \( h = 5 \) cm. Tính thể tích của hình trụ này.
Lời giải:
Áp dụng công thức:
\[ V = \pi r^2 h = \pi \cdot 3^2 \cdot 5 = 45\pi \, \text{cm}^3 \]
5. Ứng Dụng Thực Tiễn Của Hình Trụ
Hình trụ được sử dụng rộng rãi trong nhiều lĩnh vực như:
- Kiến trúc và xây dựng: thiết kế cột, trụ đỡ.
- Công nghiệp và sản xuất: ống, xi lanh, thùng chứa.
- Đồ gia dụng: lon nước ngọt, bình gas.
- Thiết bị y tế: xi lanh tiêm, ống truyền dịch.
6. Bài Tập Liên Quan
Tính Chiều Cao Của Hình Trụ
Đề bài: Diện tích xung quanh hình trụ là \( 94.2 \, \text{cm}^2 \) và bán kính đáy \( r = 3 \, \text{cm} \). Tính chiều cao \( h \) của hình trụ.
Lời giải: Sử dụng công thức \( S_{xq} = 2\pi rh \), ta có:
\[ 94.2 = 2\pi \cdot 3 \cdot h \implies h = \frac{94.2}{6\pi} \approx 5 \, \text{cm} \]
Tính Bán Kính Đáy Của Hình Trụ
Đề bài: Cho hình trụ có diện tích xung quanh là \( 125.6 \, \text{cm}^2 \) và chiều cao \( h = 4 \, \text{cm} \). Tính bán kính \( r \) của đáy.
Lời giải: Sử dụng công thức \( S_{xq} = 2\pi rh \), ta có:
\[ 125.6 = 2\pi \cdot r \cdot 4 \implies r = \frac{125.6}{8\pi} \approx 5 \, \text{cm} \]
Tính Diện Tích Toàn Phần Của Hình Trụ
Đề bài: Cho hình trụ có đường kính đáy là \( 8 \, \text{dm} \) và chiều cao là \( 6 \, \text{dm} \). Tính diện tích toàn phần của hình trụ.
Lời giải: Đường kính là \( 8 \, \text{dm} \) nên bán kính \( r = 4 \, \text{dm} \). Áp dụng công thức, ta có:
\[ S_{tp} = 2\pi r (r + h) = 2\pi \cdot 4 \cdot (4 + 6) = 80\pi \approx 251.2 \, \text{dm}^2 \]

.png)
Giới Thiệu Về Hình Trụ
Hình trụ là một hình học không gian có hai đáy là hai hình tròn bằng nhau và song song với nhau, và một mặt xung quanh bao quanh hai đáy đó. Hình trụ thường gặp trong nhiều ứng dụng thực tiễn như trong thiết kế các vật dụng hàng ngày, cơ khí, và kiến trúc.
Diện Tích Xung Quanh Của Hình Trụ
Diện tích xung quanh của hình trụ được tính bằng công thức:
\[ S_{xq} = 2 \pi r h \]
Trong đó:
- \( \pi \) (pi) là một hằng số xấp xỉ bằng 3.14
- \( r \) là bán kính đáy của hình trụ
- \( h \) là chiều cao của hình trụ
Diện Tích Toàn Phần Của Hình Trụ
Diện tích toàn phần của hình trụ bao gồm diện tích xung quanh và diện tích hai đáy, được tính bằng công thức:
\[ S_{tp} = S_{xq} + 2 S_{đ} \]
Trong đó, diện tích đáy của hình trụ là:
\[ S_{đ} = \pi r^2 \]
Ví dụ: Giả sử chúng ta có hình trụ có bán kính \( r = 4 \) và chiều cao \( h = 8 \). Diện tích xung quanh của hình trụ là:
\[ S_{xq} = 2 \cdot 3.14 \cdot 4 \cdot 8 = 201.92 \]
Diện tích đáy của hình trụ là:
\[ S_{đ} = 3.14 \cdot 4^2 = 50.24 \]
Diện tích toàn phần của hình trụ là:
\[ S_{tp} = 201.92 + 2 \cdot 50.24 = 302.4 \]
Thể Tích Của Hình Trụ
Thể tích của hình trụ được tính bằng công thức:
\[ V = S_{đ} \cdot h \]
Trong đó, diện tích đáy của hình trụ được tính như sau:
\[ S_{đ} = \pi r^2 \]
Ví dụ: Nếu hình trụ có bán kính đáy là 4 cm và chiều cao là 7 cm, thể tích của hình trụ sẽ là:
\[ V = \pi \cdot 4^2 \cdot 7 = 3.14 \cdot 16 \cdot 7 = 351.68 \, \text{cm}^3 \]
Ứng Dụng Của Hình Trụ
- Trong kiến trúc và xây dựng: các cột trụ, bồn chứa...
- Trong cơ khí: các trục, bạc đạn...
- Trong đời sống: lon nước ngọt, ống nước...
Công Thức Tính Diện Tích
Hình trụ là một hình học cơ bản có hai đáy hình tròn song song và bằng nhau, và một mặt xung quanh. Để tính diện tích của hình trụ, chúng ta cần sử dụng các công thức dưới đây:
1. Diện tích xung quanh của hình trụ:
Diện tích xung quanh của hình trụ được tính bằng công thức:
\[
S_{xq} = 2 \pi r h
\]
Trong đó:
- \(r\) là bán kính của đáy hình trụ.
- \(h\) là chiều cao của hình trụ.
2. Diện tích toàn phần của hình trụ:
Diện tích toàn phần của hình trụ bao gồm diện tích xung quanh và diện tích của hai đáy. Công thức tính diện tích toàn phần là:
\[
S_{tp} = 2 \pi r (r + h)
\]
Trong đó:
- \(r\) là bán kính của đáy hình trụ.
- \(h\) là chiều cao của hình trụ.
Ví dụ tính toán:
Ví dụ 1: Tính diện tích xung quanh của hình trụ có bán kính đáy \( r = 5 \, cm \) và chiều cao \( h = 10 \, cm \).
Giải:
\[
S_{xq} = 2 \pi r h = 2 \pi \times 5 \times 10 = 100 \pi \, cm^2
\]
Ví dụ 2: Tính diện tích toàn phần của hình trụ có bán kính đáy \( r = 3 \, cm \) và chiều cao \( h = 7 \, cm \).
Giải:
\[
S_{tp} = 2 \pi r (r + h) = 2 \pi \times 3 \times (3 + 7) = 60 \pi \, cm^2
\]
Những công thức này giúp chúng ta dễ dàng tính toán diện tích xung quanh và diện tích toàn phần của hình trụ trong các bài toán thực tế.

Công Thức Tính Thể Tích
Thể tích của hình trụ được tính bằng diện tích của mặt đáy nhân với chiều cao của hình trụ. Để tính toán thể tích, chúng ta cần biết bán kính của mặt đáy và chiều cao của hình trụ. Dưới đây là các bước chi tiết để tính thể tích hình trụ:
- Xác định bán kính của hình tròn đáy (r).
- Xác định chiều cao của hình trụ (h).
- Áp dụng công thức tính thể tích hình trụ: \( V = \pi r^2 h \)
Chúng ta có thể chia công thức này thành các bước nhỏ để dễ hiểu hơn:
- Tính diện tích của mặt đáy hình trụ: \[ A = \pi r^2 \]
- Nhân diện tích mặt đáy với chiều cao để có thể tích hình trụ: \[ V = A \cdot h = \pi r^2 h \]
Ví dụ, nếu bán kính của mặt đáy hình trụ là 3 cm và chiều cao là 5 cm, chúng ta có thể tính thể tích như sau:
| Bán kính (r) | 3 cm |
| Chiều cao (h) | 5 cm |
| Diện tích mặt đáy | \( \pi \times 3^2 = 28.27 \, \text{cm}^2 \) |
| Thể tích | \( 28.27 \times 5 = 141.35 \, \text{cm}^3 \) |
Vì vậy, thể tích của hình trụ với bán kính 3 cm và chiều cao 5 cm là 141.35 cm3.

XEM THÊM:
Ví Dụ Tính Toán
Trong phần này, chúng ta sẽ xem xét một ví dụ cụ thể để hiểu rõ hơn về cách tính thể tích và diện tích xung quanh của hình trụ. Giả sử chúng ta có một hình trụ với các thông số sau:
- Bán kính đáy (r): 4 cm
- Chiều cao (h): 10 cm
Tính Diện Tích Xung Quanh
Diện tích xung quanh của hình trụ được tính bằng công thức:
\[
S_{xq} = 2\pi rh
\]
Thay các giá trị đã cho vào công thức, ta có:
\[
S_{xq} = 2\pi \times 4 \times 10 = 80\pi \, \text{cm}^2
\]
Vậy diện tích xung quanh của hình trụ là 80π cm².
Tính Diện Tích Toàn Phần
Diện tích toàn phần của hình trụ được tính bằng công thức:
\[
S_{tp} = 2\pi r (r + h)
\]
Thay các giá trị đã cho vào công thức, ta có:
\[
S_{tp} = 2\pi \times 4 \times (4 + 10) = 2\pi \times 4 \times 14 = 112\pi \, \text{cm}^2
\]
Vậy diện tích toàn phần của hình trụ là 112π cm².
Tính Thể Tích
Thể tích của hình trụ được tính bằng công thức:
\[
V = \pi r^2 h
\]
Thay các giá trị đã cho vào công thức, ta có:
\[
V = \pi \times 4^2 \times 10 = \pi \times 16 \times 10 = 160\pi \, \text{cm}^3
\]
Vậy thể tích của hình trụ là 160π cm³.
| Tham số | Giá trị |
|---|---|
| Bán kính (r) | 4 cm |
| Chiều cao (h) | 10 cm |
| Diện tích xung quanh (Sxq) | 80π cm² |
| Diện tích toàn phần (Stp) | 112π cm² |
| Thể tích (V) | 160π cm³ |
Nhờ các bước tính toán chi tiết trên, chúng ta có thể dễ dàng xác định các thông số quan trọng của một hình trụ từ các giá trị ban đầu.

Ứng Dụng Thực Tế
Hình trụ là một hình học rất phổ biến và có nhiều ứng dụng trong đời sống hàng ngày cũng như trong các ngành công nghiệp. Dưới đây là một số ứng dụng thực tế của hình trụ:
- Trong xây dựng: Các cấu trúc hình trụ như cột trụ hỗ trợ trong các tòa nhà, cầu đường, và các công trình kiến trúc khác.
- Trong công nghiệp: Các bồn chứa, bể chứa xăng dầu, và các thiết bị chứa chất lỏng thường được thiết kế dưới dạng hình trụ để tối ưu hóa không gian và sức chứa.
- Trong gia dụng: Các vật dụng hàng ngày như lon nước giải khát, chai nước, và bình ga đều có dạng hình trụ để dễ dàng vận chuyển và sử dụng.
- Trong y tế: Các ống tiêm, chai thuốc và các thiết bị y tế khác cũng thường có dạng hình trụ để đảm bảo độ chính xác và tiện lợi trong quá trình sử dụng.
Tính Toán Thể Tích và Diện Tích Trong Ứng Dụng
Để áp dụng trong thực tế, chúng ta cần biết cách tính toán thể tích và diện tích của hình trụ. Công thức tính thể tích và diện tích đã được giới thiệu ở các phần trước, chúng ta sẽ áp dụng chúng trong một ví dụ cụ thể:
- Giả sử chúng ta có một bồn chứa nước hình trụ với bán kính r = 2 m và chiều cao h = 5 m.
Thể tích của bồn chứa được tính bằng công thức:
\[
V = \pi r^2 h = \pi \times 2^2 \times 5 = 20\pi \, \text{m}^3
\]
Vậy thể tích của bồn chứa là 20π m³.
Diện tích xung quanh của bồn chứa được tính bằng công thức:
\[
S_{xq} = 2\pi rh = 2\pi \times 2 \times 5 = 20\pi \, \text{m}^2
\]
Vậy diện tích xung quanh của bồn chứa là 20π m².
| Ứng Dụng | Hình Trụ |
|---|---|
| Xây dựng | Cột trụ, cầu đường |
| Công nghiệp | Bồn chứa, bể chứa xăng dầu |
| Gia dụng | Lon nước giải khát, chai nước, bình ga |
| Y tế | Ống tiêm, chai thuốc |
Như vậy, hình trụ không chỉ là một khái niệm trong toán học mà còn có rất nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày và trong các ngành công nghiệp khác nhau.
Bài Tập Thực Hành
Dưới đây là một số bài tập thực hành về tính diện tích và thể tích hình trụ:
Bài Tập Tính Diện Tích
-
Bài tập 1: Cho hình trụ có bán kính đáy \( r = 4 \) cm và chiều cao \( h = 6 \) cm. Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Hướng dẫn giải:
-
Diện tích xung quanh:
\[
S_{xq} = 2 \pi r h = 2 \pi \times 4 \times 6 = 48 \pi \, \text{cm}^2
\] -
Diện tích toàn phần:
\[
S_{tp} = S_{xq} + 2 S_{đáy} = 48 \pi + 2 \pi r^2 = 48 \pi + 2 \pi \times 4^2 = 48 \pi + 32 \pi = 80 \pi \, \text{cm}^2
\]
-
-
Bài tập 2: Cho hình trụ có diện tích xung quanh là 125.6 cm² và chiều cao là 10 cm. Tính bán kính đáy của hình trụ.
Hướng dẫn giải:
Sử dụng công thức tính diện tích xung quanh: \[
S_{xq} = 2 \pi r h \implies 125.6 = 2 \pi r \times 10 \implies r = \frac{125.6}{20 \pi} \approx 2 \, \text{cm}
\]
Bài Tập Tính Thể Tích
-
Bài tập 1: Cho hình trụ có bán kính đáy \( r = 5 \) cm và chiều cao \( h = 12 \) cm. Tính thể tích của hình trụ.
Hướng dẫn giải:
Thể tích hình trụ:
\[
V = \pi r^2 h = \pi \times 5^2 \times 12 = 300 \pi \, \text{cm}^3
\] -
Bài tập 2: Cho hình trụ có thể tích là 904.32 cm³ và chiều cao là 8 cm. Tính bán kính đáy của hình trụ.
Hướng dẫn giải:
Sử dụng công thức tính thể tích: \[
V = \pi r^2 h \implies 904.32 = \pi r^2 \times 8 \implies r^2 = \frac{904.32}{8 \pi} \implies r \approx 6 \, \text{cm}
\]
Tính Thể Tích Hình Trụ - Tính Diện Tích Đáy Hình Trụ Là Hình Tròn - Tính Chiều Cao Của Hình Trụ π=3,14










