Chủ đề thể tích chỏm cầu: Thể tích chỏm cầu là một chủ đề quan trọng trong hình học không gian, với nhiều ứng dụng thực tế. Bài viết này sẽ giúp bạn hiểu rõ công thức tính toán, các ứng dụng và cung cấp ví dụ minh họa chi tiết.
Mục lục
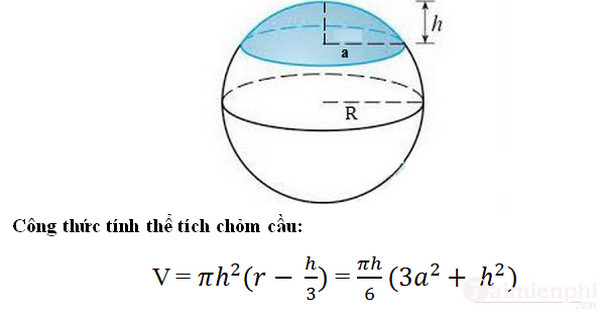
Công thức tính thể tích chỏm cầu
Thể tích chỏm cầu là một phần của thể tích hình cầu bị cắt bởi một mặt phẳng. Công thức tính thể tích của chỏm cầu có thể được diễn đạt như sau:
- Thể tích chỏm cầu:
- \( V = \frac{1}{6} \pi h (3a^2 + h^2) \)
- Trong đó:
- \( V \) là thể tích của chỏm cầu
- \( h \) là chiều cao của chỏm cầu từ mặt cắt đến đỉnh
- \( a \) là bán kính mặt đáy chỏm cầu
Ví dụ minh họa
Cho một chỏm cầu có chiều cao \( h = 2cm \) và bán kính mặt đáy \( a = 4cm \). Áp dụng công thức, ta có:
\( V = \frac{1}{6} \pi (2) (3(4^2) + 2^2) = \frac{1}{6} \pi (2) (3(16) + 4) = \frac{1}{6} \pi (2) (48 + 4) = \frac{1}{6} \pi (2) (52) = \frac{1}{6} \pi (104) = 17.33 \pi cm^3 \)
Cho một chỏm cầu có chiều cao \( h = 6cm \) và bán kính mặt cầu là \( r = 10cm \). Áp dụng công thức, ta có:
\( V = \pi h^2 (r - \frac{h}{3}) = \pi (6^2) (10 - \frac{6}{3}) = \pi (36) (10 - 2) = \pi (36) (8) = 288 \pi cm^3 \)
- Ví dụ 1:
- Ví dụ 2:

.png)
Ứng dụng của hình chỏm cầu
Hình chỏm cầu không chỉ là một khái niệm trong toán học mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và các ngành công nghiệp khác nhau. Một số ứng dụng tiêu biểu gồm:
- Thiết kế và xây dựng hệ thống đường ống
- Tính toán dung tích của các bể chứa chất lỏng
- Đánh giá khối lượng và trọng lượng của các vật thể
- Chế tạo và sản xuất các thiết bị điện tử, máy móc
Các bài tập tham khảo
Tính thể tích của chỏm cầu có chiều cao \( h = 3cm \) và bán kính mặt đáy \( a = 5cm \).
Tính diện tích bề mặt của chỏm cầu có chiều cao \( h = 4cm \) và bán kính mặt đáy \( a = 6cm \).
- Bài tập 1:
- Bài tập 2:
Lời giải bài tập 1:
Áp dụng công thức, ta có:
\( V = \frac{1}{6} \pi h (3a^2 + h^2) = \frac{1}{6} \pi (3) (3(5^2) + 3^2) = \frac{1}{6} \pi (3) (75 + 9) = \frac{1}{6} \pi (3) (84) = \frac{1}{6} \pi (252) = 42 \pi cm^3 \)
Lời giải bài tập 2:
Áp dụng công thức diện tích bề mặt:
\( S = 2 \pi rh = 2 \pi (6) (4) = 48 \pi cm^2 \)

Ứng dụng của hình chỏm cầu
Hình chỏm cầu không chỉ là một khái niệm trong toán học mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và các ngành công nghiệp khác nhau. Một số ứng dụng tiêu biểu gồm:
- Thiết kế và xây dựng hệ thống đường ống
- Tính toán dung tích của các bể chứa chất lỏng
- Đánh giá khối lượng và trọng lượng của các vật thể
- Chế tạo và sản xuất các thiết bị điện tử, máy móc

XEM THÊM:
Các bài tập tham khảo
Tính thể tích của chỏm cầu có chiều cao \( h = 3cm \) và bán kính mặt đáy \( a = 5cm \).
Tính diện tích bề mặt của chỏm cầu có chiều cao \( h = 4cm \) và bán kính mặt đáy \( a = 6cm \).
- Bài tập 1:
- Bài tập 2:
Lời giải bài tập 1:
Áp dụng công thức, ta có:
\( V = \frac{1}{6} \pi h (3a^2 + h^2) = \frac{1}{6} \pi (3) (3(5^2) + 3^2) = \frac{1}{6} \pi (3) (75 + 9) = \frac{1}{6} \pi (3) (84) = \frac{1}{6} \pi (252) = 42 \pi cm^3 \)
Lời giải bài tập 2:
Áp dụng công thức diện tích bề mặt:
\( S = 2 \pi rh = 2 \pi (6) (4) = 48 \pi cm^2 \)

Các bài tập tham khảo
Tính thể tích của chỏm cầu có chiều cao \( h = 3cm \) và bán kính mặt đáy \( a = 5cm \).
Tính diện tích bề mặt của chỏm cầu có chiều cao \( h = 4cm \) và bán kính mặt đáy \( a = 6cm \).
- Bài tập 1:
- Bài tập 2:
Lời giải bài tập 1:
Áp dụng công thức, ta có:
\( V = \frac{1}{6} \pi h (3a^2 + h^2) = \frac{1}{6} \pi (3) (3(5^2) + 3^2) = \frac{1}{6} \pi (3) (75 + 9) = \frac{1}{6} \pi (3) (84) = \frac{1}{6} \pi (252) = 42 \pi cm^3 \)
Lời giải bài tập 2:
Áp dụng công thức diện tích bề mặt:
\( S = 2 \pi rh = 2 \pi (6) (4) = 48 \pi cm^2 \)
Định Nghĩa Thể Tích Chỏm Cầu
Hình chỏm cầu là phần của hình cầu bị cắt bởi một mặt phẳng. Nếu mặt phẳng này cắt qua tâm của hình cầu, hình chỏm cầu sẽ là một bán cầu. Thể tích chỏm cầu được tính dựa trên bán kính của hình cầu và chiều cao từ mặt cắt đến đỉnh chỏm cầu.
Thể tích của chỏm cầu có thể được tính bằng công thức sau:
Công thức tổng quát:
\[ V = \pi h^2 \left( r - \frac{h}{3} \right) \]
Trong đó:
- \( V \): Thể tích của chỏm cầu
- \( r \): Bán kính của hình cầu
- \( h \): Chiều cao từ mặt cắt đến đỉnh chỏm cầu
Công thức trên có thể được chi tiết hóa như sau:
\[ V = \frac{\pi h^2 (3r - h)}{3} \]
Ví dụ, nếu bán kính của hình cầu là \( r = 10 \) cm và chiều cao của chỏm cầu là \( h = 4 \) cm, thể tích của chỏm cầu được tính như sau:
\[ V = \frac{\pi \cdot 4^2 \cdot (3 \cdot 10 - 4)}{3} = \frac{\pi \cdot 16 \cdot 26}{3} = \frac{416\pi}{3} \approx 436.33 \, cm^3 \]
Như vậy, thể tích của chỏm cầu với các giá trị trên là khoảng 436.33 cm3.

Công Thức Tính Thể Tích Chỏm Cầu
Thể tích của một khối chỏm cầu có thể được tính bằng cách sử dụng công thức dựa trên bán kính mặt cầu và chiều cao của chỏm cầu. Dưới đây là công thức chi tiết:
-
Cho một khối chỏm cầu với bán kính mặt cầu là \( R \) và chiều cao từ mặt cắt đến đỉnh chỏm cầu là \( h \).
Công thức tính thể tích \( V \) của khối chỏm cầu là:
\[ V = \frac{\pi h^2}{3} (3R - h) \]
-
Nếu biết độ dài bán kính đáy chỏm cầu là \( a \) và chiều cao là \( h \), thì công thức thể tích có thể viết lại như sau:
\[ V = \frac{1}{6} \pi h (3a^2 + h^2) \]
Để hiểu rõ hơn, ta sẽ áp dụng công thức vào một ví dụ cụ thể:
- Ví dụ: Tính thể tích của một khối chỏm cầu có bán kính mặt cầu \( R = 10 \) cm và chiều cao \( h = 6 \) cm.
- Áp dụng công thức:
- \[ V = \frac{\pi h^2}{3} (3R - h) = \frac{\pi (6)^2}{3} (3 \times 10 - 6) = 252 \pi \text{ cm}^3 \]

Ví Dụ Minh Họa
Dưới đây là một số ví dụ minh họa về cách tính thể tích của chỏm cầu. Các ví dụ này sẽ giúp bạn hiểu rõ hơn về cách áp dụng công thức trong thực tế.
- Ví dụ 1: Cho hình chỏm cầu có chiều cao \( h = 2 \) cm và bán kính \( r = 4 \) cm. Áp dụng công thức \( V = \frac{\pi h^2}{3}(3r - h) \), ta có:
Chiều cao (h) 2 cm Bán kính (r) 4 cm Thể tích (V) \( V = \frac{\pi (2)^2}{3}(3 \cdot 4 - 2) = \frac{4\pi}{3}(12 - 2) = \frac{4\pi}{3} \cdot 10 = \frac{40\pi}{3} \approx 41.89 \, cm^3 \) - Ví dụ 2: Xét hình chỏm cầu với chiều cao \( h = 3 \) cm và bán kính \( r = 6 \) cm. Công thức thể tích chỏm cầu là \( V = \frac{\pi h^2}{3}(3r - h) \):
Chiều cao (h) 3 cm Bán kính (r) 6 cm Thể tích (V) \( V = \frac{\pi (3)^2}{3}(3 \cdot 6 - 3) = \frac{9\pi}{3}(18 - 3) = 3\pi \cdot 15 = 45\pi \approx 141.37 \, cm^3 \)
Ứng Dụng Thực Tế
Thể tích chỏm cầu không chỉ là một khái niệm trong toán học mà còn có nhiều ứng dụng thực tế trong đời sống và các ngành công nghiệp khác nhau. Dưới đây là một số ứng dụng tiêu biểu:
- Thiết kế và xây dựng đường ống: Công thức tính thể tích chỏm cầu được sử dụng trong công nghiệp xây dựng và thiết kế hệ thống đường ống, giúp tính toán dung tích cần thiết, đảm bảo tính ổn định và hiệu quả của đường ống.
- Tính toán dung tích của bể chứa chất lỏng: Ứng dụng này giúp trong việc đo lường và không gian hình học, như tính dung tích của bể chứa chất lỏng.
- Đánh giá khối lượng và trọng lượng: Việc tính toán thể tích chỏm cầu giúp trong việc đánh giá khối lượng và trọng lượng của các vật thể có hình dạng tương tự, áp dụng trong ngành sản xuất và nghiên cứu vật liệu.
- Chế tạo và sản xuất: Hình chỏm cầu được sử dụng để tạo ra vỏ bảo vệ cho các thiết bị điện tử, bầu tiên tiến cho máy móc, đèn pha hiện đại, và làm khay đựng hàng hóa với cấu trúc vững chắc.
Qua những ví dụ trên, có thể thấy hình chỏm cầu không chỉ gói gọn trong sách giáo khoa mà còn góp phần vào sự phát triển của nhiều lĩnh vực khác nhau, từ kiến trúc đến công nghiệp sản xuất. Hiểu biết về công thức và ứng dụng của hình chỏm cầu sẽ giúp ích rất nhiều cho các nhà thiết kế, kỹ sư, và nghệ nhân trong quá trình sáng tạo và tối ưu hóa sản phẩm của mình.
Tham Khảo
Dưới đây là danh sách các tài liệu tham khảo hữu ích cho việc nghiên cứu và tính toán thể tích chỏm cầu, cùng với các ứng dụng thực tế của công thức này:
- Công thức tính thể tích chỏm cầu: Tài liệu Toán học Cơ bản
- Ứng dụng hình chỏm cầu trong thiết kế kiến trúc: Báo cáo Kỹ thuật
- Các bài tập thực hành về thể tích chỏm cầu: Sách giáo khoa Toán học lớp 12
Các tài liệu trên cung cấp cái nhìn tổng quan về các khía cạnh lý thuyết và thực tiễn của thể tích chỏm cầu, bao gồm cả cách tính toán và các ví dụ minh họa.
Sử dụng công thức:
V h = 1 3 π h 2 ( 3 r 2 + h 2 )để tính thể tích của một chỏm cầu.
Để biết thêm chi tiết và các ví dụ cụ thể, vui lòng tham khảo các tài liệu liệt kê ở trên.























