Chủ đề vòng tròn lượng giác: Vòng tròn lượng giác là một công cụ quan trọng trong toán học, giúp hiểu sâu sắc về mối quan hệ giữa góc và các hàm số lượng giác. Bài viết này sẽ giới thiệu chi tiết về các công thức, ứng dụng và bài tập liên quan đến vòng tròn lượng giác.
Mục lục
- Vòng Tròn Lượng Giác
- Giới Thiệu Về Vòng Tròn Lượng Giác
- Công Thức Cơ Bản Của Vòng Tròn Lượng Giác
- Ứng Dụng Của Vòng Tròn Lượng Giác
- Góc và Cung Đặc Biệt Trong Vòng Tròn Lượng Giác
- Công Thức Các Cung Liên Kết
- Bài Tập Vận Dụng Vòng Tròn Lượng Giác
- YOUTUBE: Khám phá kỹ thuật vòng tròn lượng giác qua video hướng dẫn dễ hiểu nhất của Thầy VNA. Video bài 5 dành cho học sinh lớp 12 giúp nắm vững kiến thức quan trọng trong môn Vật lý.
Vòng Tròn Lượng Giác
Vòng tròn lượng giác là một công cụ quan trọng trong toán học, đặc biệt là trong việc học và hiểu các hàm lượng giác cơ bản như sin, cos, và tan. Vòng tròn lượng giác có tâm tại gốc tọa độ (0, 0) và bán kính bằng 1.
Các Giá Trị Lượng Giác Cơ Bản
Trong vòng tròn lượng giác, các giá trị lượng giác cơ bản được tính dựa trên tọa độ của các điểm trên vòng tròn. Dưới đây là bảng các giá trị lượng giác của một số góc phổ biến:
| Góc | Sin | Cos | Tan |
|---|---|---|---|
| 0° (\(0\)) | 0 | 1 | 0 |
| 30° (\(\frac{\pi}{6}\)) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (\(\frac{\pi}{4}\)) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (\(\frac{\pi}{3}\)) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (\(\frac{\pi}{2}\)) | 1 | 0 | Không xác định |
Góc và Cung Đặc Biệt trong Vòng Tròn Lượng Giác
Vòng tròn lượng giác chứa nhiều góc và cung đặc biệt. Các góc này có giá trị lượng giác đặc biệt giúp đơn giản hóa việc giải toán và ứng dụng thực tế:
- Góc 0° (0 radian): Điểm bắt đầu, sin = 0 và cos = 1.
- Góc 90° (\(\frac{\pi}{2}\) radian): Điểm ở đỉnh, sin = 1 và cos = 0.
- Góc 180° (\(\pi\) radian): Điểm đối diện điểm bắt đầu, sin = 0 và cos = -1.
- Góc 270° (\(\frac{3\pi}{2}\) radian): Điểm ở cạnh dưới, sin = -1 và cos = 0.
- Góc 360° (2\(\pi\) radian): Hoàn thành một vòng tròn, trở lại điểm bắt đầu.
Các cung này chia vòng tròn lượng giác thành bốn phần tư với các giá trị dấu khác nhau của sin và cos:
| Phần tư | Sin | Cos | Tan |
|---|---|---|---|
| I (0° đến 90°) | Dương | Dương | Dương |
| II (90° đến 180°) | Dương | Âm | Âm |
| III (180° đến 270°) | Âm | Âm | Dương |
| IV (270° đến 360°) | Âm | Dương | Âm |
Công Thức Tính Giá Trị Lượng Giác
Dưới đây là một số công thức cơ bản và quan trọng liên quan đến các giá trị lượng giác:
- \(\sin(\alpha + k \cdot \frac{2\pi}{n}) = \sin(\alpha)\)
- \(\cos(\alpha + k \cdot \frac{2\pi}{n}) = \cos(\alpha)\)
- \(\tan(\alpha + k \cdot \frac{2\pi}{n}) = \tan(\alpha)\)
Ứng Dụng của Vòng Tròn Lượng Giác
Vòng tròn lượng giác có nhiều ứng dụng trong các lĩnh vực khác nhau:
- Hình học: Giúp tính toán các đo lường và quan hệ trong không gian ba chiều.
- Vật lý: Sử dụng trong việc mô phỏng và tính toán các hiện tượng như chuyển động và sóng.
- Kỹ thuật: Áp dụng trong thiết kế các hệ thống điều khiển và cảm biến.
- Thiết kế đồ họa và trò chơi: Tạo ra các hiệu ứng đặc biệt và tính toán vị trí, hướng di chuyển của các đối tượng.

.png)
Giới Thiệu Về Vòng Tròn Lượng Giác
Vòng tròn lượng giác là một công cụ quan trọng trong toán học, đặc biệt là trong lĩnh vực lượng giác. Đây là một đường tròn đơn vị, có bán kính bằng 1 và tâm tại gốc tọa độ (0, 0) trên mặt phẳng tọa độ. Vòng tròn này giúp biểu diễn và tính toán các giá trị lượng giác của các góc một cách trực quan và dễ hiểu.
Vòng tròn lượng giác được sử dụng để biểu diễn các hàm số lượng giác cơ bản như sin, cos, và tan. Trong đó:
- Sin (Sine): Là tọa độ y của điểm trên vòng tròn lượng giác.
- Cos (Cosine): Là tọa độ x của điểm trên vòng tròn lượng giác.
- Tan (Tangent): Được tính bằng tỉ số giữa tọa độ y và tọa độ x của điểm (y/x).
Dưới đây là bảng các giá trị lượng giác cơ bản của một số góc phổ biến:
| Góc | Sin | Cos | Tan |
|---|---|---|---|
| 0° (\(0\)) | 0 | 1 | 0 |
| 30° (\(\frac{\pi}{6}\)) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (\(\frac{\pi}{4}\)) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (\(\frac{\pi}{3}\)) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (\(\frac{\pi}{2}\)) | 1 | 0 | KXD (Không xác định) |
Vòng tròn lượng giác không chỉ giúp hiểu rõ hơn về các giá trị lượng giác mà còn ứng dụng rộng rãi trong nhiều lĩnh vực như:
- Hình Học: Tính toán các góc và khoảng cách trong không gian ba chiều.
- Vật Lý: Mô phỏng và tính toán các hiện tượng như chuyển động và sóng.
- Kỹ Thuật: Thiết kế các hệ thống điều khiển và cảm biến.
- Thiết Kế Đồ Họa và Trò Chơi: Tạo hiệu ứng đặc biệt và tính toán vị trí, hướng di chuyển của các đối tượng.
Với vòng tròn lượng giác, việc học và ứng dụng các công thức lượng giác trở nên dễ dàng và trực quan hơn rất nhiều, giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
Công Thức Cơ Bản Của Vòng Tròn Lượng Giác
Vòng tròn lượng giác là một công cụ quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các hàm số lượng giác. Dưới đây là các công thức cơ bản của vòng tròn lượng giác, được chia nhỏ để dễ dàng theo dõi và áp dụng.
1. Định Nghĩa và Các Giá Trị Cơ Bản
- Định lý Pythagoras trên vòng tròn lượng giác:
\[\sin^2\theta + \cos^2\theta = 1\]
- Tính chất tuần hoàn: Các hàm số sin, cos tuần hoàn với chu kỳ \(2\pi\).
- \[\sin(\theta + 2\pi) = \sin\theta\]
- \[\cos(\theta + 2\pi) = \cos\theta\]
2. Các Công Thức Lượng Giác Cơ Bản
- Hàm số sin:
\[\sin(x \pm y) = \sin(x) \cos(y) \pm \cos(x) \sin(y)\]
- Hàm số cos:
\[\cos(x \pm y) = \cos(x) \cos(y) \mp \sin(x) \sin(y)\]
- Hàm số tan:
\[\tan(x \pm y) = \frac{\tan(x) \pm \tan(y)}{1 \mp \tan(x) \tan(y)}\]
3. Công Thức Góc Kép
- Sin của góc kép:
\[\sin(2x) = 2 \sin(x) \cos(x)\]
- Cos của góc kép:
\[\cos(2x) = \cos^2(x) - \sin^2(x)\]
- Tan của góc kép:
\[\tan(2x) = \frac{2 \tan(x)}{1 - \tan^2(x)}\]
4. Công Thức Liên Quan Đến Các Hàm Số Khác
- Hàm số cot:
\[\cot(x) = \frac{1}{\tan(x)}\]
- Hàm số sec:
\[\sec(x) = \frac{1}{\cos(x)}\]
- Hàm số csc:
\[\csc(x) = \frac{1}{\sin(x)}\]
5. Bảng Giá Trị Lượng Giác Cơ Bản
| Góc (°) | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| \(\sin\) | 0 | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
| \(\cos\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | 0 |
| \(\tan\) | 0 | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | Không xác định |

Ứng Dụng Của Vòng Tròn Lượng Giác
Vòng tròn lượng giác là công cụ hữu ích trong nhiều lĩnh vực khoa học và kỹ thuật. Dưới đây là một số ứng dụng chính của vòng tròn lượng giác:
Trong Toán Học
Vòng tròn lượng giác giúp biểu diễn và giải quyết các phương trình lượng giác. Các giá trị sin, cos, tan của các góc đặc biệt có thể được xác định dễ dàng nhờ vào các tọa độ trên vòng tròn.
- Giải phương trình lượng giác: Vòng tròn lượng giác cho phép xác định các giá trị xung quanh vòng tròn, giúp giải các phương trình lượng giác phức tạp.
- Biểu diễn góc: Các góc trong lượng giác có thể được biểu diễn trực quan trên vòng tròn, giúp hiểu rõ hơn về các mối quan hệ giữa các góc và giá trị lượng giác.
Trong Vật Lý
Vòng tròn lượng giác được sử dụng rộng rãi trong vật lý, đặc biệt trong các bài toán liên quan đến dao động và sóng.
- Dao động điều hòa: Vòng tròn lượng giác giúp mô tả các chuyển động dao động điều hòa, trong đó các giá trị sin và cos biểu diễn vị trí và vận tốc theo thời gian.
- Sóng và giao thoa: Trong các hiện tượng sóng, vòng tròn lượng giác được sử dụng để tính toán các pha sóng và phân tích các mẫu giao thoa.
Trong Kỹ Thuật
Vòng tròn lượng giác cũng có nhiều ứng dụng trong kỹ thuật, đặc biệt trong các lĩnh vực như kỹ thuật điện và cơ khí.
- Phân tích tín hiệu: Các kỹ thuật phân tích tín hiệu sử dụng các hàm lượng giác để biểu diễn và phân tích các tín hiệu điện.
- Chuyển động cơ học: Trong cơ khí, vòng tròn lượng giác giúp mô tả các chuyển động quay và các hiện tượng dao động trong các hệ thống cơ khí.
Trong Khoa Học Máy Tính
Vòng tròn lượng giác được sử dụng trong đồ họa máy tính và các thuật toán liên quan đến hình ảnh và âm thanh.
- Đồ họa máy tính: Các phép biến đổi hình học sử dụng các hàm lượng giác để xoay, dịch chuyển và biến dạng các hình ảnh.
- Xử lý tín hiệu: Trong xử lý âm thanh và hình ảnh, các hàm lượng giác giúp phân tích và tổng hợp các tín hiệu.
Nhờ vào tính ứng dụng rộng rãi và khả năng giải quyết nhiều bài toán phức tạp, vòng tròn lượng giác đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau.
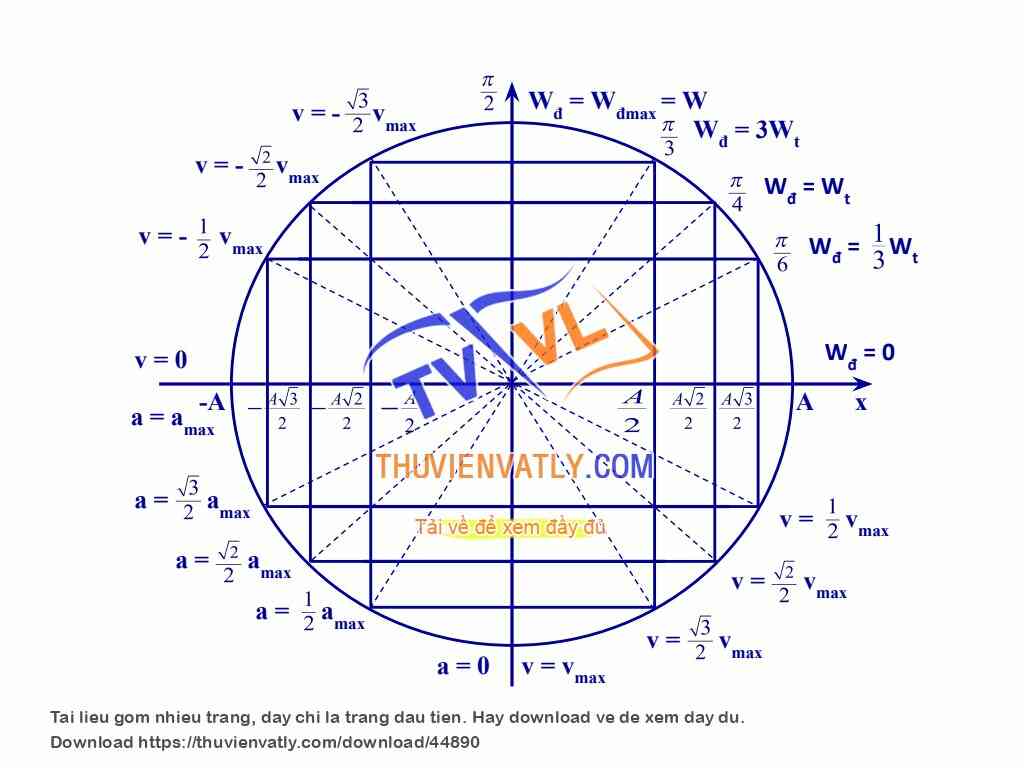
Góc và Cung Đặc Biệt Trong Vòng Tròn Lượng Giác
Trong toán học, vòng tròn lượng giác là một công cụ quan trọng để biểu diễn các hàm lượng giác. Đặc biệt, các góc và cung lượng giác đặc biệt giúp chúng ta hiểu rõ hơn về các giá trị của sin, cos và tan.
Góc Đặc Biệt
Các góc đặc biệt trên vòng tròn lượng giác bao gồm:
- Góc 0° (0 radian): Điểm bắt đầu trên vòng tròn lượng giác, nơi sin = 0 và cos = 1.
- Góc 90° (\(\frac{\pi}{2}\) radian): Điểm ở đỉnh vòng tròn lượng giác, nơi sin = 1 và cos = 0.
- Góc 180° (\(\pi\) radian): Điểm đối diện với điểm bắt đầu, nơi sin = 0 và cos = -1.
- Góc 270° (\(\frac{3\pi}{2}\) radian): Điểm ở cạnh dưới của vòng tròn, nơi sin = -1 và cos = 0.
- Góc 360° (2\(\pi\) radian): Hoàn thành một vòng tròn lượng giác, trở lại điểm bắt đầu.
Cung Đặc Biệt
Các cung đặc biệt trên vòng tròn lượng giác chia nó thành các phần tư:
| Phần tư | Góc | Sin | Cos | Tan |
|---|---|---|---|---|
| I | 0° đến 90° | Dương | Dương | Dương |
| II | 90° đến 180° | Dương | Âm | Âm |
| III | 180° đến 270° | Âm | Âm | Dương |
| IV | 270° đến 360° | Âm | Dương | Âm |
Giá Trị Lượng Giác tại Các Góc Đặc Biệt
Dưới đây là bảng giá trị lượng giác cho một số góc đặc biệt thường gặp:
| Góc | Sin | Cos | Tan |
|---|---|---|---|
| 0° (0 rad) | 0 | 1 | 0 |
| 30° (\(\frac{\pi}{6}\) rad) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (\(\frac{\pi}{4}\) rad) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (\(\frac{\pi}{3}\) rad) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (\(\frac{\pi}{2}\) rad) | 1 | 0 | Không xác định |
Các Cung Liên Kết
Các cung lượng giác liên kết nhau cũng có các giá trị lượng giác liên quan:
- Góc đối nhau: \( \sin(\pi - \theta) = \sin(\theta) \)
- Góc bù nhau: \( \sin(\pi + \theta) = -\sin(\theta) \)
- Góc phụ nhau: \( \sin(\frac{\pi}{2} - \theta) = \cos(\theta) \)
- Góc hơn kém: \( \sin(\theta + 2\pi) = \sin(\theta) \)

Công Thức Các Cung Liên Kết
Trong toán học, công thức các cung liên kết là một phần quan trọng của lượng giác. Các công thức này giúp tính toán các giá trị lượng giác của các góc đặc biệt và cung liên kết. Dưới đây là một số công thức cơ bản của các cung liên kết:
Góc Đối Nhau
- \(\sin(180^\circ - \alpha) = \sin(\alpha)\)
- \(\cos(180^\circ - \alpha) = -\cos(\alpha)\)
- \(\tan(180^\circ - \alpha) = -\tan(\alpha)\)
- \(\cot(180^\circ - \alpha) = -\cot(\alpha)\)
Góc Bù Nhau
- \(\sin(90^\circ - \alpha) = \cos(\alpha)\)
- \(\cos(90^\circ - \alpha) = \sin(\alpha)\)
- \(\tan(90^\circ - \alpha) = \cot(\alpha)\)
- \(\cot(90^\circ - \alpha) = \tan(\alpha)\)
Góc Phụ Nhau
- \(\sin(90^\circ + \alpha) = \cos(\alpha)\)
- \(\cos(90^\circ + \alpha) = -\sin(\alpha)\)
- \(\tan(90^\circ + \alpha) = -\cot(\alpha)\)
- \(\cot(90^\circ + \alpha) = -\tan(\alpha)\)
Góc Hơn Kém
- \(\sin(360^\circ - \alpha) = -\sin(\alpha)\)
- \(\cos(360^\circ - \alpha) = \cos(\alpha)\)
- \(\tan(360^\circ - \alpha) = -\tan(\alpha)\)
- \(\cot(360^\circ - \alpha) = -\cot(\alpha)\)
Việc nắm vững các công thức này giúp giải quyết các bài toán lượng giác một cách nhanh chóng và hiệu quả. Chúng đặc biệt hữu ích trong việc giải phương trình lượng giác và tính toán các giá trị lượng giác của các góc đặc biệt.
XEM THÊM:
Bài Tập Vận Dụng Vòng Tròn Lượng Giác
Để củng cố kiến thức về vòng tròn lượng giác, dưới đây là một số bài tập vận dụng. Các bài tập này giúp bạn làm quen với việc sử dụng các công thức và định lý liên quan đến vòng tròn lượng giác trong các bài toán thực tế.
Bài Tập Cơ Bản
-
Bài 1: Tìm giá trị của sin, cos, tan cho các góc đặc biệt: 0°, 30°, 45°, 60°, 90°.
Hướng dẫn: Sử dụng bảng giá trị lượng giác của các góc đặc biệt.
-
Bài 2: Cho điểm M nằm trên đường tròn lượng giác, biết tọa độ của M là (0.5, √3/2). Tìm góc α mà điểm M tạo với trục Ox.
Hướng dẫn: Sử dụng hàm cos để tìm góc α.
-
Bài 3: Giải phương trình lượng giác: \( \sin x = \frac{1}{2} \) trên đoạn [0, 2π].
Hướng dẫn: Sử dụng các giá trị đặc biệt của sin.
Bài Tập Nâng Cao
-
Bài 1: Tìm các nghiệm của phương trình lượng giác: \( \sin 2x = \cos x \) trên đoạn [0, 2π].
Hướng dẫn: Sử dụng công thức nhân đôi và các công thức biến đổi lượng giác để giải phương trình.
-
Bài 2: Chứng minh rằng: \( \sin^2 x + \cos^2 x = 1 \) cho mọi giá trị của x.
Hướng dẫn: Sử dụng định lý Pythagore trong tam giác vuông.
-
Bài 3: Giải phương trình: \( \tan x = \frac{\sqrt{3}}{3} \) trên đoạn [0, 2π].
Hướng dẫn: Sử dụng giá trị đặc biệt của tan và các tính chất của hàm số lượng giác.
Bài Tập Thực Tế
-
Bài 1: Trong một dao động điều hòa, một vật có phương trình dao động: \( x = 5\cos(2πt + π/6) \). Tính vận tốc của vật tại thời điểm t = 1s.
Hướng dẫn: Sử dụng đạo hàm của phương trình dao động để tìm vận tốc.
-
Bài 2: Một bánh xe quay với tốc độ góc không đổi, cần tìm vị trí của điểm trên vành bánh xe sau thời gian t = 2s nếu tốc độ góc là ω = π/4 rad/s.
Hướng dẫn: Sử dụng công thức góc quay để tính vị trí.
-
Bài 3: Một con lắc đơn dao động với biên độ góc 30°. Tính lực kéo về tác dụng lên vật nặng của con lắc tại thời điểm góc lệch khỏi vị trí cân bằng là 15°.
Hướng dẫn: Sử dụng công thức lực kéo về trong dao động điều hòa.





















