Chủ đề bảng xếp hạng bóng đá ngoại hạng anh mới: Bảng xếp hạng bóng đá Ngoại hạng Anh mới nhất mùa giải 2024/2025 được cập nhật liên tục, cung cấp thông tin chính xác về vị trí của các đội bóng sau mỗi vòng đấu. Khám phá chi tiết những biến động trên bảng xếp hạng và phân tích các yếu tố ảnh hưởng đến thành tích của từng câu lạc bộ.
Mục lục
- Bảng Xếp Hạng Bóng Đá Ngoại Hạng Anh Mới Nhất
- Mục Lục Tổng Hợp Các Bài Viết Về Bảng Xếp Hạng Ngoại Hạng Anh
- 10 Dạng Bài Tập Toán, Lý, Tiếng Anh Có Lời Giải Hoàn Chỉnh
- Bài Tập Toán 1: Giải Phương Trình Bậc Hai
- Bài Tập Toán 2: Tính Giá Trị Cực Trị Của Hàm Số
- Bài Tập Toán 3: Ứng Dụng Tích Phân Tính Diện Tích
- Bài Tập Toán 4: Phân Tích Đa Thức Thành Nhân Tử
- Bài Tập Toán 5: Giải Hệ Phương Trình Tuyến Tính
- Bài Tập Lý 1: Tính Toán Điện Trở Trong Mạch Điện Song Song
- Bài Tập Lý 2: Định Luật Bảo Toàn Năng Lượng Trong Dao Động
- Bài Tập Lý 3: Tính Tốc Độ Ánh Sáng Trong Môi Trường Khác Nhau
- Bài Tập Tiếng Anh 1: Viết Lại Câu Giữ Nguyên Nghĩa
- Bài Tập Tiếng Anh 2: Điền Từ Vào Đoạn Văn Cho Sẵn
Bảng Xếp Hạng Bóng Đá Ngoại Hạng Anh Mới Nhất
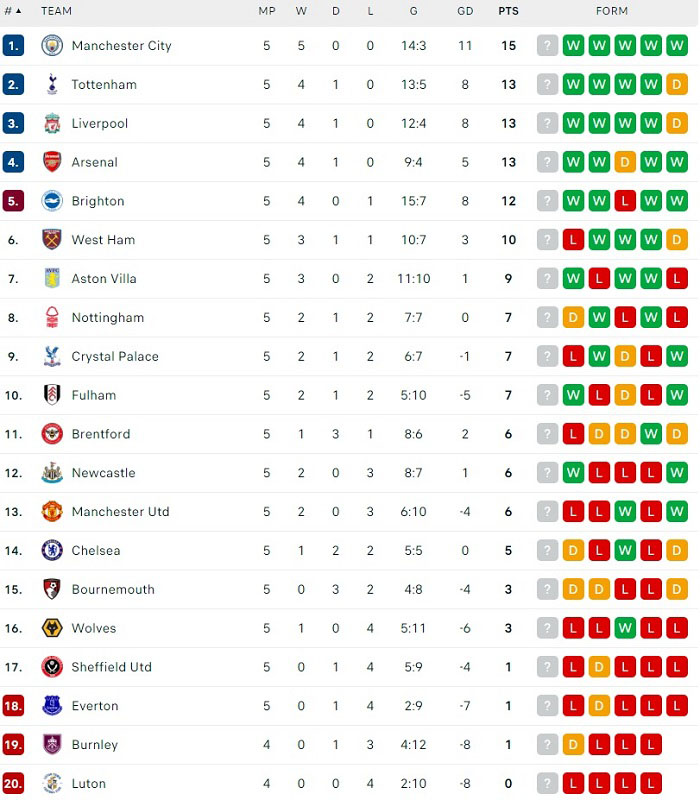
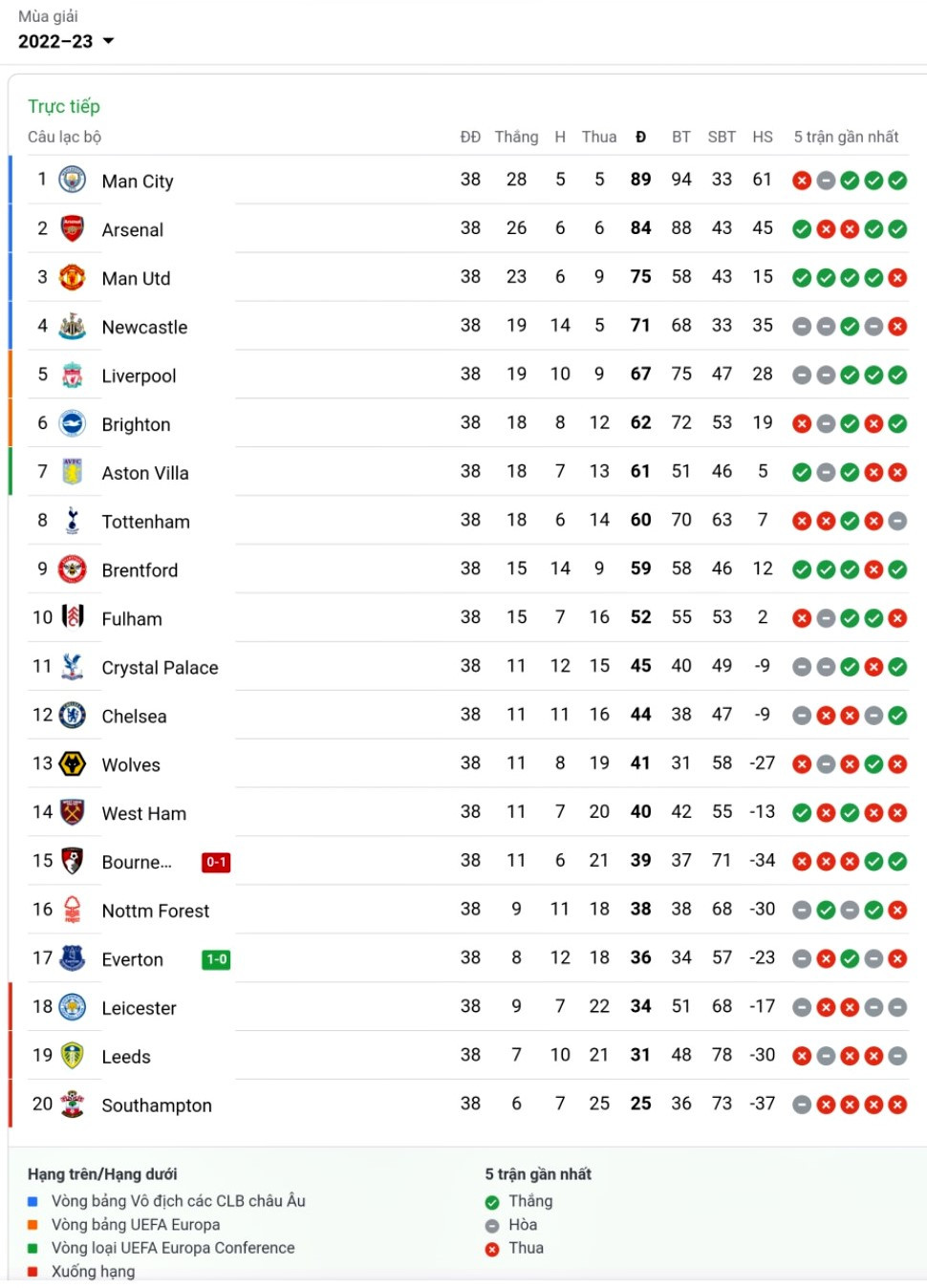
Bảng xếp hạng bóng đá Ngoại Hạng Anh 2024/2025 sau vòng đấu gần nhất cho thấy sự cạnh tranh khốc liệt giữa các câu lạc bộ hàng đầu. Dưới đây là bảng xếp hạng chi tiết:
| Vị trí | Đội bóng | Trận đấu | Thắng | Hòa | Thua | Hiệu số | Điểm |
|---|---|---|---|---|---|---|---|
| 1 | Brighton | 2 | 2 | 0 | 0 | +5 | 6 |
| 2 | Manchester City | 2 | 2 | 0 | 0 | +4 | 6 |
| 3 | Liverpool | 2 | 1 | 1 | 0 | +3 | 4 |
| 4 | Arsenal | 2 | 1 | 1 | 0 | +2 | 4 |
Thông Tin Nổi Bật
- Brighton đang dẫn đầu bảng với phong độ xuất sắc, toàn thắng sau 2 trận.
- Manchester City duy trì sức mạnh với chuỗi trận thắng liên tiếp, sẵn sàng bảo vệ ngôi vương.
- Liverpool và Arsenal cũng khẳng định vị thế trong top 4, tiếp tục bám đuổi quyết liệt.
Lịch Thi Đấu Vòng Tiếp Theo
Vòng đấu tiếp theo sẽ diễn ra với những trận cầu hấp dẫn:
- Brighton vs Manchester United: Một trận đấu đầy thử thách cho đội đầu bảng.
- Liverpool vs Brentford: Liverpool sẽ cố gắng duy trì vị trí cao trên bảng xếp hạng.
- Arsenal vs Aston Villa: Arsenal đặt mục tiêu giành trọn 3 điểm.
Kết Luận
Cuộc đua ở Ngoại Hạng Anh mùa này đang ngày càng hấp dẫn với sự cạnh tranh khốc liệt giữa các đội bóng lớn. Người hâm mộ sẽ còn chứng kiến nhiều bất ngờ và kịch tính trong những vòng đấu tiếp theo.
.png)
Mục Lục Tổng Hợp Các Bài Viết Về Bảng Xếp Hạng Ngoại Hạng Anh
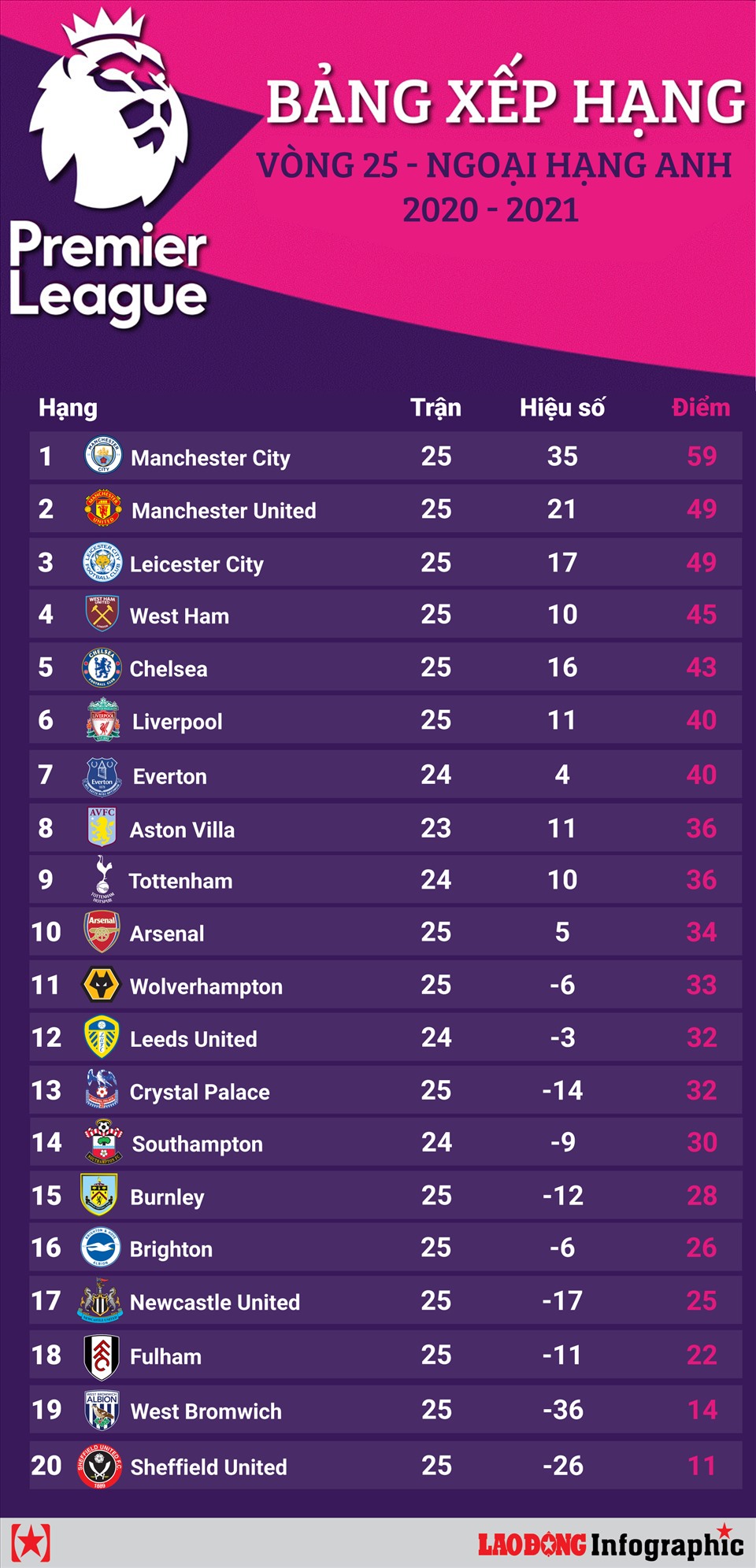
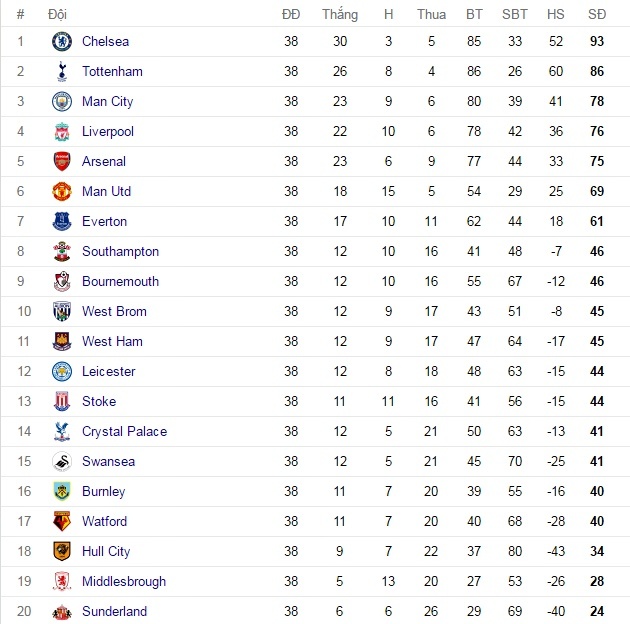
Bảng Xếp Hạng Ngoại Hạng Anh 2024/25 Mới Nhất
Thông tin cập nhật về bảng xếp hạng của giải Ngoại Hạng Anh mùa giải 2024/25, bao gồm thứ hạng của các đội bóng, số trận thắng, hòa, thua, và điểm số hiện tại.
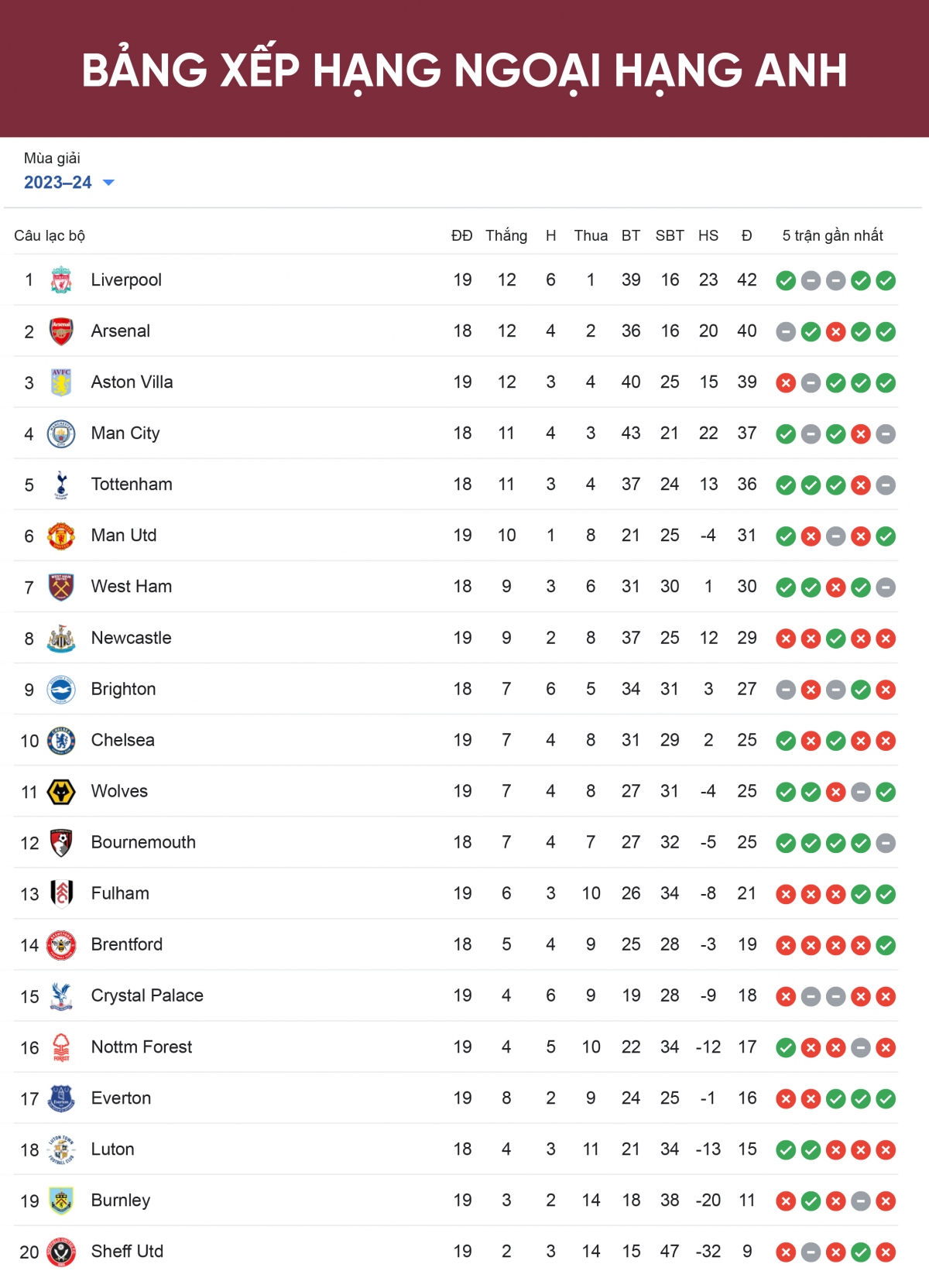
Arsenal Và Manchester United: Sự Biến Động Trên Bảng Xếp Hạng
Phân tích sự cạnh tranh khốc liệt giữa Arsenal và Manchester United khi cả hai đội đều gặp khó khăn trong việc giữ vững vị trí trên bảng xếp hạng.
Cuộc Đua Vô Địch Và Những Thay Đổi Trong Top 4
Những đội bóng dẫn đầu trong cuộc đua vô địch, sự thay đổi liên tục của top 4 đội đứng đầu, và cơ hội để các đội bóng khác lọt vào top này.
Những Trận Đấu Đáng Chú Ý Của Mùa Giải
Tổng hợp các trận đấu quan trọng và kịch tính nhất trong mùa giải 2024/25, những kết quả bất ngờ và ảnh hưởng của chúng đến bảng xếp hạng.
Phân Tích Chiến Thuật Và Phong Độ Của Các Đội Bóng
Đánh giá chi tiết về chiến thuật, phong độ thi đấu của các đội bóng hàng đầu trong giải, và tác động của chúng đến vị trí trên bảng xếp hạng.
Dự Đoán Kết Quả Cuối Mùa Và Ảnh Hưởng Đến Bảng Xếp Hạng
Dự đoán thứ hạng cuối mùa giải dựa trên phong độ hiện tại, lịch thi đấu còn lại, và các yếu tố khác ảnh hưởng đến bảng xếp hạng.
10 Dạng Bài Tập Toán, Lý, Tiếng Anh Có Lời Giải Hoàn Chỉnh
Việc luyện tập với các dạng bài tập khác nhau sẽ giúp học sinh nắm vững kiến thức và nâng cao kỹ năng giải quyết vấn đề. Dưới đây là 10 dạng bài tập tiêu biểu trong các môn Toán, Lý, và Tiếng Anh, cùng với lời giải chi tiết giúp các em học sinh có thể tự rèn luyện và kiểm tra kiến thức của mình.
- Toán học:
- Phương trình bậc hai: Bài tập giải phương trình bậc hai với đầy đủ các bước như đặt ẩn phụ, tính nghiệm và kiểm tra kết quả.
- Hệ phương trình tuyến tính: Bài tập áp dụng phương pháp cộng, trừ và thế để giải các hệ phương trình tuyến tính.
- Hình học không gian: Các bài tập tính toán thể tích và diện tích của các khối đa diện như hình lập phương, hình lăng trụ.
- Vật lý:
- Định luật bảo toàn năng lượng: Bài tập áp dụng định luật bảo toàn năng lượng để tính công, năng lượng và hiệu suất của các hệ vật lý.
- Điện học cơ bản: Các bài tập về mạch điện đơn giản bao gồm tính toán dòng điện, hiệu điện thế và điện trở.
- Cơ học: Bài tập về chuyển động thẳng đều và chuyển động rơi tự do, tính toán các đại lượng như vận tốc, quãng đường, và thời gian.
- Tiếng Anh:
- Reading Comprehension: Bài tập đọc hiểu với các đoạn văn ngắn, kèm theo các câu hỏi trắc nghiệm nhằm kiểm tra khả năng hiểu nội dung và từ vựng của học sinh.
- Writing Practice: Bài tập viết luận với các chủ đề quen thuộc, giúp học sinh rèn luyện kỹ năng viết và phát triển tư duy logic.
- Grammar and Vocabulary: Bài tập ngữ pháp về thì động từ, mệnh đề quan hệ, và từ vựng theo chủ đề.
Mỗi dạng bài tập đều được trình bày chi tiết và có lời giải hoàn chỉnh, giúp học sinh dễ dàng nắm bắt được các phương pháp giải quyết và ứng dụng trong các bài kiểm tra thực tế. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn trong học tập và đạt kết quả cao trong các kỳ thi.

Bài Tập Toán 1: Giải Phương Trình Bậc Hai
Giải phương trình bậc hai là một phần quan trọng trong chương trình Toán lớp 1. Phương trình bậc hai có dạng tổng quát như sau:
\[ ax^2 + bx + c = 0 \]
Trong đó:
- a, b, c là các hệ số thực
- x là ẩn số cần tìm
Để giải phương trình bậc hai, chúng ta sẽ thực hiện theo các bước sau:
- Xác định các hệ số a, b, c: Đầu tiên, chúng ta cần xác định các giá trị của a, b và c từ phương trình.
- Tính delta (\(\Delta\)):
Delta được tính theo công thức:
\[ \Delta = b^2 - 4ac \]
- Xét dấu của delta:
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có một nghiệm kép.
- Nếu \(\Delta < 0\), phương trình vô nghiệm.
- Tính nghiệm của phương trình:
- Nếu \(\Delta > 0\):
Nghiệm thứ nhất:
\[ x_1 = \frac{-b + \sqrt{\Delta}}{2a} \]
Nghiệm thứ hai:
\[ x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
- Nếu \(\Delta = 0\):
Nghiệm kép:
\[ x = \frac{-b}{2a} \]
- Nếu \(\Delta < 0\):
Phương trình không có nghiệm thực.
- Nếu \(\Delta > 0\):
Việc hiểu và áp dụng đúng công thức giải phương trình bậc hai không chỉ giúp các em học sinh giải quyết các bài toán cơ bản mà còn là nền tảng để học các kiến thức Toán học cao hơn trong tương lai.
Bài Tập Toán 2: Tính Giá Trị Cực Trị Của Hàm Số
Trong toán học, giá trị cực trị của hàm số là một khái niệm quan trọng, giúp xác định điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trên một khoảng. Để giải quyết bài toán tính giá trị cực trị của hàm số, chúng ta cần thực hiện các bước sau:
-
Xác định hàm số: Giả sử hàm số cần tìm cực trị có dạng:
\[ y = f(x) \]
-
Tính đạo hàm: Đạo hàm của hàm số sẽ cho chúng ta biết tốc độ thay đổi của hàm số tại một điểm bất kỳ.
\[ f'(x) = \frac{dy}{dx} \]
-
Tìm điểm dừng: Giải phương trình:
\[ f'(x) = 0 \]
Các nghiệm của phương trình này là những điểm mà hàm số có thể đạt cực trị.
-
Xác định loại cực trị: Tính đạo hàm bậc hai để xác định xem tại các điểm dừng có phải là điểm cực đại, cực tiểu, hay không có cực trị.
Nếu \[ f''(x) > 0 \] thì \( x \) là điểm cực tiểu.
Nếu \[ f''(x) < 0 \] thì \( x \) là điểm cực đại.
Nếu \[ f''(x) = 0 \] thì cần xét tiếp tính chất của hàm số để kết luận.
-
Tính giá trị cực trị: Thay các điểm cực trị tìm được vào hàm số ban đầu để tính giá trị tương ứng:
\[ y_{max/min} = f(x) \]
Qua các bước trên, chúng ta có thể tính chính xác giá trị cực trị của hàm số trong các bài toán toán học phức tạp, từ đó giúp giải quyết nhiều vấn đề thực tế và nâng cao khả năng tư duy toán học.

Bài Tập Toán 3: Ứng Dụng Tích Phân Tính Diện Tích
Trong chương trình toán học lớp 3, tích phân là một công cụ quan trọng được sử dụng để tính diện tích dưới các đường cong. Việc áp dụng tích phân không chỉ giúp học sinh hiểu rõ hơn về hình học mà còn rèn luyện kỹ năng giải toán phức tạp hơn.
1. Khái niệm cơ bản về tích phân
Tích phân được hiểu đơn giản là phép tính diện tích của vùng nằm dưới đồ thị của hàm số. Để tính tích phân, chúng ta sử dụng các công thức toán học cụ thể.
Công thức cơ bản của tích phân là:
Trong đó:
- \(a\) và \(b\) là các giới hạn của tích phân.
- \(f(x)\) là hàm số cần tính diện tích dưới đồ thị.
2. Ví dụ thực tế
Xét bài toán tính diện tích của hình thang cong giới hạn bởi đồ thị hàm số \(y = x^2\), trục hoành và hai đường thẳng \(x = 1\) và \(x = 3\).
Để tính diện tích, ta sử dụng tích phân:
Giải:
Vậy, diện tích của hình thang cong là 8.67 đơn vị diện tích.
3. Bài tập thực hành
Để nắm vững kiến thức, học sinh nên luyện tập thêm các bài tập dưới đây:
- Tính diện tích vùng nằm dưới đồ thị hàm số \(y = 2x + 1\) từ \(x = 0\) đến \(x = 2\).
- Tính diện tích hình phẳng giới hạn bởi đường cong \(y = \sin(x)\) và trục hoành từ \(x = 0\) đến \(x = \pi\).
- Tính diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \(y = \frac{1}{x}\) và các trục tọa độ từ \(x = 1\) đến \(x = 4\).
4. Kết luận
Ứng dụng tích phân để tính diện tích là một kỹ năng quan trọng trong toán học. Thông qua các bài tập thực hành, học sinh có thể hiểu sâu hơn về cách tính tích phân cũng như áp dụng chúng trong các bài toán thực tế.
XEM THÊM:
Bài Tập Toán 4: Phân Tích Đa Thức Thành Nhân Tử
Phân tích đa thức thành nhân tử là một trong những kỹ năng quan trọng trong toán học. Đây là bước cơ bản để giải quyết nhiều bài toán phức tạp hơn. Dưới đây là hướng dẫn chi tiết từng bước giúp các em học sinh lớp 4 nắm vững phương pháp phân tích đa thức thành nhân tử.
1. Phân Tích Đa Thức Bằng Cách Đặt Nhân Tử Chung
Khi gặp đa thức có các hạng tử chứa một nhân tử chung, chúng ta sẽ đặt nhân tử chung ra ngoài dấu ngoặc:
Ví dụ: Phân tích đa thức \(6x^2 + 9x\) thành nhân tử:
Ở đây, \(3x\) là nhân tử chung được đặt ra ngoài.
2. Phân Tích Đa Thức Bằng Phương Pháp Nhóm Hạng Tử
Phương pháp nhóm hạng tử thường được sử dụng khi không có nhân tử chung cho tất cả các hạng tử, nhưng có thể nhóm chúng lại để xuất hiện nhân tử chung:
Ví dụ: Phân tích đa thức \(x^3 + x^2 + x + 1\) thành nhân tử:
Nhóm \(x^3 + x^2\) và \(x + 1\) để tạo thành hai nhóm có nhân tử chung.
3. Phân Tích Đa Thức Bậc Hai Bằng Công Thức
Với những đa thức bậc hai dạng \(ax^2 + bx + c\), chúng ta có thể phân tích bằng cách sử dụng công thức nghiệm:
Ví dụ: Phân tích đa thức \(x^2 + 5x + 6\) thành nhân tử:
Dựa trên công thức nghiệm, chúng ta tìm được hai nghiệm của đa thức và viết nó dưới dạng tích.
4. Bài Tập Thực Hành
- Phân tích đa thức \(4y^2 - 12y\) thành nhân tử.
- Phân tích đa thức \(x^2 - 9\) thành nhân tử.
- Phân tích đa thức \(x^2 - 4x + 4\) thành nhân tử.
5. Kết Luận
Việc phân tích đa thức thành nhân tử không chỉ giúp đơn giản hóa các biểu thức toán học mà còn là nền tảng để giải quyết các phương trình và bất phương trình. Thực hành thường xuyên sẽ giúp các em nắm vững phương pháp và áp dụng dễ dàng trong các bài toán phức tạp hơn.
Bài Tập Toán 5: Giải Hệ Phương Trình Tuyến Tính
Hệ phương trình tuyến tính là một trong những kiến thức quan trọng trong chương trình Toán lớp 5. Dưới đây là các bước cụ thể để giải một hệ phương trình tuyến tính với hai ẩn.
- Xác định hệ phương trình: Một hệ phương trình tuyến tính bao gồm hai phương trình với hai ẩn \(x\) và \(y\). Ví dụ: \[ \begin{cases} 2x + 3y = 6 \\ 4x - y = 5 \end{cases} \]
- Sử dụng phương pháp thế: Từ một trong hai phương trình, giải ẩn này theo ẩn kia. Chẳng hạn, từ phương trình thứ hai: \[ y = 4x - 5 \] Sau đó, thế giá trị của \(y\) vào phương trình thứ nhất: \[ 2x + 3(4x - 5) = 6 \]
- Giải phương trình một ẩn: Giải phương trình vừa thu được để tìm \(x\). \[ 2x + 12x - 15 = 6 \Rightarrow 14x = 21 \Rightarrow x = \frac{21}{14} = 1.5 \]
- Tìm giá trị của ẩn còn lại: Thay giá trị của \(x\) vào một trong hai phương trình ban đầu để tìm \(y\). \[ y = 4(1.5) - 5 = 6 - 5 = 1 \]
- Kết luận: Vậy nghiệm của hệ phương trình là \(x = 1.5\) và \(y = 1\). \[ \boxed{(x, y) = \left(1.5, 1\right)} \]
Trên đây là các bước cụ thể để giải một hệ phương trình tuyến tính đơn giản. Việc nắm vững phương pháp giải này sẽ giúp các em học sinh tự tin hơn khi gặp các bài toán tương tự.

Bài Tập Lý 1: Tính Toán Điện Trở Trong Mạch Điện Song Song
Trong mạch điện song song, các điện trở được mắc theo cách sao cho các đầu của chúng được nối trực tiếp với nhau. Điều này dẫn đến mỗi điện trở đều nhận được cùng một hiệu điện thế từ nguồn, và cường độ dòng điện tổng được chia đều qua các nhánh.
Khi tính toán tổng điện trở của một mạch điện song song, công thức tổng quát được sử dụng như sau:
Công thức:
Trong đó:
- \(R_{\text{tổng}}\) là điện trở tổng của mạch.
- \(R_1, R_2, R_3, \dots, R_n\) là các điện trở riêng lẻ trong mạch.
Để giải một bài toán tính điện trở trong mạch song song, bạn có thể làm theo các bước sau:
- Xác định các giá trị điện trở cụ thể của từng nhánh trong mạch.
- Áp dụng công thức tổng quát để tính giá trị nghịch đảo của điện trở tổng.
- Đảo ngược kết quả để tìm điện trở tổng thực tế của mạch.
- Kiểm tra lại các bước tính toán để đảm bảo tính chính xác.
Ví dụ, nếu bạn có ba điện trở song song với các giá trị lần lượt là 2Ω, 3Ω và 6Ω, điện trở tổng sẽ được tính như sau:
Kết quả:
Kết luận: Tổng điện trở của một mạch điện song song luôn nhỏ hơn điện trở nhỏ nhất trong số các điện trở thành phần.
Bài Tập Lý 2: Định Luật Bảo Toàn Năng Lượng Trong Dao Động
Định luật bảo toàn năng lượng là một nguyên lý quan trọng trong vật lý, đặc biệt khi áp dụng vào các hệ dao động cơ học. Dưới đây là một ví dụ cụ thể và các bước giải chi tiết.
Ví dụ: Một con lắc lò xo có khối lượng \( m = 0,5 \, kg \) và độ cứng \( k = 200 \, N/m \) đang dao động điều hòa. Biên độ dao động là \( A = 0,1 \, m \). Hãy tính vận tốc của vật khi nó đi qua vị trí cân bằng.
Lời giải:
Tính năng lượng toàn phần của hệ:
Năng lượng toàn phần \( E \) của hệ dao động điều hòa chỉ phụ thuộc vào biên độ dao động và được tính bằng công thức:
\[ E = \frac{1}{2}kA^2 \]Thay số vào ta có:
\[ E = \frac{1}{2} \times 200 \, N/m \times (0,1 \, m)^2 = 1 \, J \]Tính vận tốc của vật khi đi qua vị trí cân bằng:
Khi vật đi qua vị trí cân bằng, toàn bộ năng lượng của hệ là động năng. Động năng \( K \) được tính bằng:
\[ K = \frac{1}{2}mv^2 \]Từ đó, vận tốc \( v \) được xác định bằng:
\[ v = \sqrt{\frac{2K}{m}} \]Vì tại vị trí cân bằng, \( K = E \), nên:
\[ v = \sqrt{\frac{2 \times 1 \, J}{0,5 \, kg}} = 2 \, m/s \]
Vậy, vận tốc của vật khi đi qua vị trí cân bằng là \( 2 \, m/s \).
Bài Tập Lý 3: Tính Tốc Độ Ánh Sáng Trong Môi Trường Khác Nhau
Trong bài học này, chúng ta sẽ cùng nhau tìm hiểu và tính toán tốc độ ánh sáng khi nó truyền qua các môi trường khác nhau như không khí, nước, và thủy tinh. Tốc độ ánh sáng trong môi trường chân không là \(3 \times 10^8\) m/s. Tuy nhiên, khi ánh sáng đi qua các môi trường khác, tốc độ của nó sẽ thay đổi tùy theo chiết suất của môi trường đó.
Dưới đây là các bước để tính tốc độ ánh sáng trong môi trường khác nhau:
- Biết tốc độ ánh sáng trong chân không là \(c = 3 \times 10^8\) m/s.
- Biết chiết suất của môi trường \(n\), công thức tính tốc độ ánh sáng trong môi trường đó là: \[ v = \frac{c}{n} \] với \(v\) là tốc độ ánh sáng trong môi trường đó.
- Áp dụng công thức trên để tính tốc độ ánh sáng trong các môi trường khác nhau. Ví dụ:
- Trong không khí, chiết suất \(n \approx 1\), do đó: \[ v_{\text{không khí}} = \frac{3 \times 10^8}{1} = 3 \times 10^8 \text{ m/s} \]
- Trong nước, chiết suất \(n \approx 1.33\), do đó: \[ v_{\text{nước}} = \frac{3 \times 10^8}{1.33} \approx 2.25 \times 10^8 \text{ m/s} \]
- Trong thủy tinh, chiết suất \(n \approx 1.5\), do đó: \[ v_{\text{thủy tinh}} = \frac{3 \times 10^8}{1.5} = 2 \times 10^8 \text{ m/s} \]
Qua bài tập này, chúng ta thấy rằng tốc độ ánh sáng giảm đi khi truyền qua các môi trường có chiết suất lớn hơn 1. Điều này có ý nghĩa quan trọng trong các ứng dụng như kính quang học và công nghệ viễn thông.
Bài Tập Tiếng Anh 1: Viết Lại Câu Giữ Nguyên Nghĩa
Trong phần này, bạn sẽ được hướng dẫn cách viết lại câu mà vẫn giữ nguyên ý nghĩa gốc. Đây là một kỹ năng quan trọng giúp bạn nắm vững ngữ pháp tiếng Anh và mở rộng khả năng diễn đạt của mình. Dưới đây là các bước chi tiết để thực hiện bài tập này:
- Hiểu rõ ý nghĩa của câu gốc: Trước khi viết lại câu, bạn cần đảm bảo rằng mình hiểu chính xác nội dung của câu ban đầu. Điều này giúp bạn giữ nguyên ý nghĩa khi viết lại.
- Sử dụng cấu trúc ngữ pháp khác: Một trong những cách viết lại câu là thay đổi cấu trúc ngữ pháp, chẳng hạn như chuyển từ câu chủ động sang câu bị động, sử dụng từ đồng nghĩa, hoặc thay đổi thứ tự từ.
- Giữ nguyên ý nghĩa: Dù thay đổi cấu trúc hay từ vựng, bạn cần đảm bảo rằng câu viết lại không thay đổi ý nghĩa gốc.
- Kiểm tra và so sánh: Sau khi viết lại câu, bạn nên kiểm tra và so sánh với câu gốc để chắc chắn rằng ý nghĩa không bị thay đổi.
Dưới đây là một số ví dụ:
| Câu gốc | Câu viết lại |
| Theo dõi bảng xếp hạng bóng đá Ngoại Hạng Anh là một thói quen của tôi. | It is my habit to follow the Premier League football rankings. |
| Tôi bắt đầu xem các trận đấu của giải Ngoại Hạng Anh từ năm 2020. | I have been watching Premier League matches since 2020. |
| Đội bóng này đã giành được vị trí cao trên bảng xếp hạng. | This team has secured a high position in the rankings. |
Bạn hãy thử tự viết lại câu theo các bước trên và đối chiếu với câu gốc để thấy sự khác biệt và hiệu quả của cách diễn đạt mới.
Bài Tập Tiếng Anh 2: Điền Từ Vào Đoạn Văn Cho Sẵn
Trong bài tập này, các em học sinh sẽ được thực hành kỹ năng điền từ vào đoạn văn dựa trên những gợi ý đã có sẵn. Đây là một phương pháp hiệu quả để cải thiện vốn từ vựng và khả năng hiểu ngữ cảnh của học sinh.
- Bước 1: Đọc kỹ đoạn văn để nắm bắt nội dung chính và xác định vị trí cần điền từ.
- Bước 2: Sử dụng ngữ cảnh của câu trước và sau để suy luận từ cần điền. Chú ý đến các từ khóa hoặc cụm từ gợi ý.
- Bước 3: Xem xét các từ ngữ đã biết và thử điền từ thích hợp vào chỗ trống. Nếu từ điền vào hợp lý về cả ngữ pháp và ngữ nghĩa, bạn có thể chuyển sang chỗ trống tiếp theo.
- Bước 4: Sau khi hoàn thành, hãy đọc lại toàn bộ đoạn văn để kiểm tra xem các từ đã điền có giúp đoạn văn trở nên mạch lạc và hợp lý chưa.
Dưới đây là một ví dụ minh họa:
| Câu hỏi | Đoạn văn và các chỗ trống | Gợi ý từ |
| Ví dụ 1 | The Premier League is one of the most popular football leagues in the world. It is known for its _______ matches and talented players. Each season, teams compete fiercely to secure the top _______ in the league table. | exciting, position |
| Ví dụ 2 | Manchester United has been one of the top teams in the Premier League for many years. Fans _______ support their team through thick and thin, hoping for another league title. | always, title |
Hãy áp dụng các bước trên để hoàn thành bài tập một cách tốt nhất. Chúc các em học tốt!