Chủ đề kết quả bóng đá nữ asiad việt nam: Bài viết này cung cấp cái nhìn tổng quan và chi tiết về kết quả bóng đá nữ của đội tuyển Việt Nam tại ASIAD 2023. Chúng tôi sẽ tổng hợp những thông tin mới nhất, phân tích các trận đấu và đưa ra những nhận định chuyên sâu về hành trình của đội tuyển nữ Việt Nam tại giải đấu quan trọng này.
Mục lục
- Kết quả bóng đá nữ ASIAD 2023: Việt Nam
- Mục lục tổng hợp kết quả bóng đá nữ ASIAD Việt Nam
- 10 Dạng bài tập Toán, Lý, hoặc Tiếng Anh có lời giải hoàn chỉnh
- Bài tập Toán 1: Giải phương trình bậc hai
- Bài tập Toán 2: Tính diện tích hình tròn
- Bài tập Lý 1: Tính lực đàn hồi trong lò xo
- Bài tập Lý 2: Phân tích chuyển động thẳng đều
- Bài tập Tiếng Anh 1: Chia thì đúng trong câu
- Bài tập Tiếng Anh 2: Chọn từ đúng điền vào chỗ trống
- Bài tập Toán 3: Tính thể tích hình lập phương
- Bài tập Lý 3: Phân tích lực tác dụng lên vật chuyển động
- Bài tập Tiếng Anh 3: Viết lại câu sử dụng cấu trúc khác
- Bài tập Toán 4: Giải hệ phương trình tuyến tính
Kết quả bóng đá nữ ASIAD 2023: Việt Nam
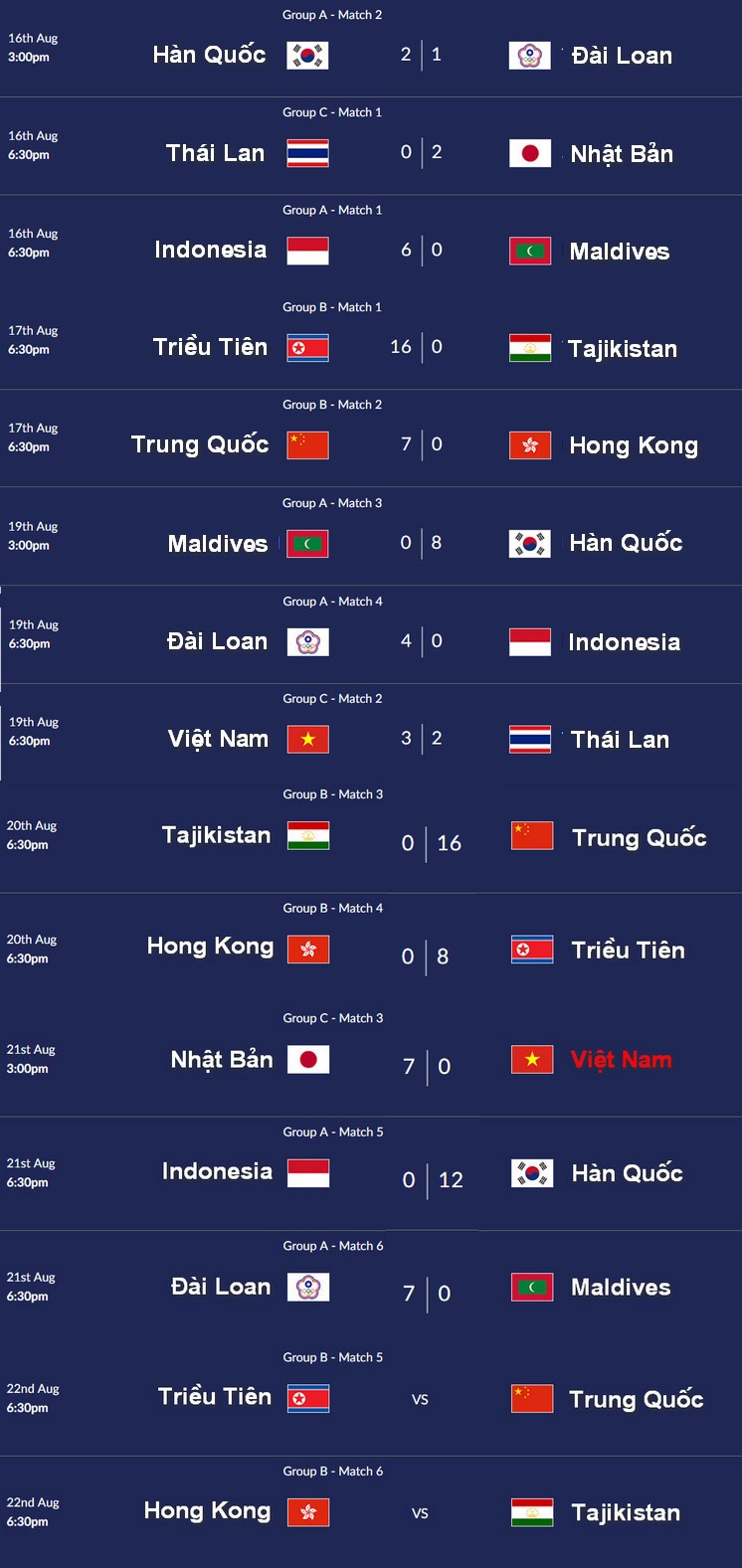
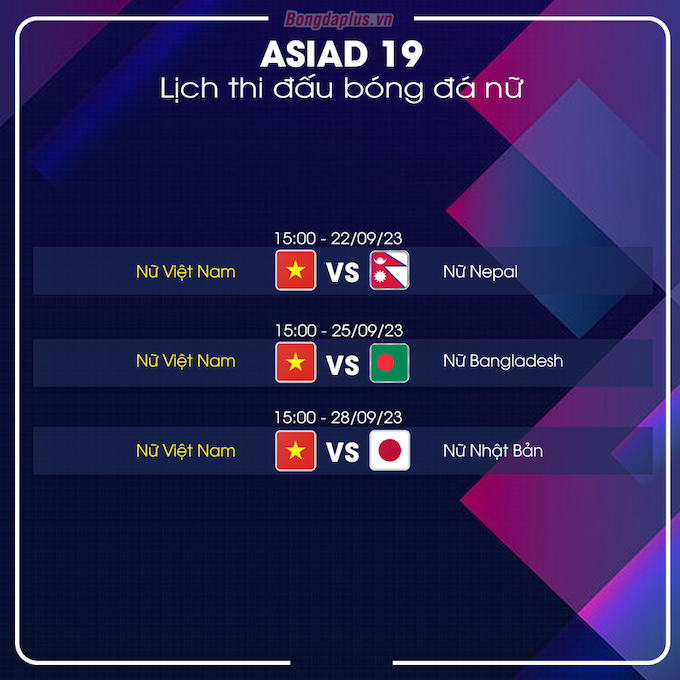
Dưới đây là tổng hợp chi tiết và đầy đủ về kết quả của đội tuyển bóng đá nữ Việt Nam tại ASIAD 2023:
Vòng Bảng
| Ngày | Trận đấu | Kết quả |
|---|---|---|
| 22/09/2023 | Việt Nam vs Bangladesh | 6-1 |
| 25/09/2023 | Việt Nam vs Nepal | 2-0 |
| 28/09/2023 | Việt Nam vs Nhật Bản | 0-3 |
Thành tích Vòng Bảng
Đội tuyển nữ Việt Nam đứng thứ 2 bảng D với 6 điểm sau 3 trận, ghi được 8 bàn thắng và để thủng lưới 4 bàn.
Vòng Tứ Kết
Đội tuyển nữ Việt Nam gặp đội tuyển nữ Hàn Quốc vào ngày 30/09/2023. Trận đấu kết thúc với tỉ số 0-4 nghiêng về Hàn Quốc, kết thúc hành trình của đội tuyển nữ Việt Nam tại ASIAD 2023.
Nhận định và Kết Luận
- Đội tuyển nữ Việt Nam đã thể hiện sự nỗ lực và tinh thần chiến đấu mạnh mẽ, đặc biệt là trong các trận đấu với Bangladesh và Nepal.
- Mặc dù không tiến xa hơn vòng tứ kết, nhưng đội tuyển đã để lại ấn tượng với tinh thần thi đấu không bỏ cuộc.
ASIAD 2023 là một cơ hội quý giá để đội tuyển nữ Việt Nam tích lũy kinh nghiệm và chuẩn bị cho các giải đấu quốc tế sắp tới.

.png)
Mục lục tổng hợp kết quả bóng đá nữ ASIAD Việt Nam
- Tổng quan kết quả bóng đá nữ ASIAD Việt Nam
Một cái nhìn tổng quan về hành trình của đội tuyển nữ Việt Nam tại ASIAD 2023, bao gồm các trận đấu, thành tích và xếp hạng trong các vòng đấu.
- Diễn biến chi tiết từng trận đấu
Việt Nam vs Bangladesh
Phân tích chiến thắng ấn tượng 6-1 trước Bangladesh, với các pha ghi bàn đẹp mắt và chiến thuật thông minh của đội tuyển.
Việt Nam vs Nepal
Đánh giá trận đấu với Nepal, nơi Việt Nam thể hiện sức mạnh vượt trội với chiến thắng 2-0.
Việt Nam vs Nhật Bản
Phân tích trận đấu với Nhật Bản, đội tuyển mạnh nhất bảng, kết quả và những bài học rút ra.
- Xếp hạng và thành tích của đội tuyển nữ Việt Nam
Tổng kết thành tích của đội tuyển sau vòng bảng và đánh giá cơ hội đi tiếp của đội trong các vòng sau.
- Phân tích chiến thuật của đội tuyển nữ Việt Nam
Phân tích lối chơi và chiến thuật được áp dụng trong các trận đấu, cùng những điểm mạnh và điểm cần cải thiện.
- Những ngôi sao sáng giá trong đội hình
Danh sách và đánh giá về những cầu thủ nổi bật nhất trong đội tuyển nữ Việt Nam tại ASIAD 2023.
- Dự đoán tương lai của đội tuyển nữ Việt Nam
Dự đoán những cơ hội và thách thức mà đội tuyển nữ Việt Nam có thể đối mặt trong các giải đấu quốc tế sắp tới.
10 Dạng bài tập Toán, Lý, hoặc Tiếng Anh có lời giải hoàn chỉnh
- Toán: Giải phương trình bậc hai
Giải phương trình bậc hai dạng \[ax^2 + bx + c = 0\] bằng công thức nghiệm: \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
- Toán: Tính diện tích hình tròn
Tính diện tích hình tròn có bán kính \(r\) bằng công thức: \[S = \pi r^2\]
- Lý: Tính lực đàn hồi của lò xo
Tính lực đàn hồi theo định luật Hooke: \[F = -k \Delta x\], trong đó \(k\) là độ cứng của lò xo và \(\Delta x\) là độ biến dạng.
- Lý: Phân tích chuyển động thẳng đều
Tính vận tốc trong chuyển động thẳng đều: \[v = \frac{s}{t}\], trong đó \(s\) là quãng đường và \(t\) là thời gian.
- Tiếng Anh: Chia thì đúng trong câu
Hoàn thành câu với thì hiện tại hoàn thành: "She has lived in this city for 5 years."
- Tiếng Anh: Chọn từ đúng điền vào chỗ trống
Chọn từ đúng: "He is interested in learning new languages."
- Toán: Tính thể tích hình lập phương
Tính thể tích của một hình lập phương cạnh \(a\) bằng công thức: \[V = a^3\]
- Lý: Phân tích lực tác dụng lên vật chuyển động
Xác định các lực tác dụng lên vật chuyển động trên mặt phẳng ngang không ma sát.
- Tiếng Anh: Viết lại câu sử dụng cấu trúc khác
Viết lại câu: "He can't afford to buy a new car." thành "He doesn't have enough money to buy a new car."
- Toán: Giải hệ phương trình tuyến tính
Giải hệ phương trình tuyến tính hai ẩn: \[\begin{cases} 2x + 3y = 5 \\ 4x - y = 1 \end{cases}\]

Bài tập Toán 1: Giải phương trình bậc hai
Phương trình bậc hai có dạng tổng quát:
Trong đó:
- \(a\), \(b\), \(c\) là các hệ số với \(a \neq 0\).
- \(x\) là ẩn số cần tìm.
Để giải phương trình bậc hai, ta sử dụng công thức nghiệm:
Quy trình giải bài tập cụ thể như sau:
- Đầu tiên, xác định các hệ số \(a\), \(b\), và \(c\) từ phương trình.
- Tính \(\Delta\) (delta) theo công thức: \[ \Delta = b^2 - 4ac \]
- Xét dấu của \(\Delta\):
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có nghiệm kép.
- Nếu \(\Delta < 0\), phương trình vô nghiệm.
- Tính nghiệm (nếu có) bằng cách thay \(\Delta\) vào công thức nghiệm.
- Viết kết luận về nghiệm của phương trình.
Ví dụ:
Giải phương trình: \(2x^2 - 4x - 6 = 0\)
- Bước 1: Xác định hệ số: \(a = 2\), \(b = -4\), \(c = -6\).
- Bước 2: Tính \(\Delta = (-4)^2 - 4 \cdot 2 \cdot (-6) = 16 + 48 = 64\).
- Bước 3: Vì \(\Delta > 0\), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{-(-4) + \sqrt{64}}{2 \cdot 2} = \frac{4 + 8}{4} = 3 \] \[ x_2 = \frac{-(-4) - \sqrt{64}}{2 \cdot 2} = \frac{4 - 8}{4} = -1 \]
- Bước 4: Kết luận: Phương trình có hai nghiệm \(x_1 = 3\) và \(x_2 = -1\).

Bài tập Toán 2: Tính diện tích hình tròn
Diện tích của một hình tròn được tính bằng công thức:
Trong đó:
- \(S\) là diện tích hình tròn.
- \(r\) là bán kính của hình tròn.
- \(\pi\) là hằng số Pi, xấp xỉ bằng 3.14159.
Quy trình giải bài tập cụ thể như sau:
- Xác định bán kính \(r\) của hình tròn.
- Thay giá trị bán kính \(r\) vào công thức \(S = \pi r^2\).
- Tính giá trị của diện tích \(S\) bằng cách nhân giá trị \(r^2\) với \(\pi\).
- Viết kết luận về diện tích của hình tròn.
Ví dụ:
Tính diện tích của hình tròn có bán kính \(r = 5 \, \text{cm}\).
- Bước 1: Xác định bán kính: \(r = 5 \, \text{cm}\).
- Bước 2: Thay \(r = 5\) vào công thức: \[ S = \pi \times (5)^2 = \pi \times 25 \]
- Bước 3: Tính diện tích: \[ S \approx 3.14159 \times 25 = 78.54 \, \text{cm}^2 \]
- Bước 4: Kết luận: Diện tích của hình tròn là khoảng \(78.54 \, \text{cm}^2\).

Bài tập Lý 1: Tính lực đàn hồi trong lò xo
Lực đàn hồi của lò xo được tính bằng định luật Hooke với công thức:
Trong đó:
- \(F\) là lực đàn hồi (đơn vị: Newton, N).
- \(k\) là độ cứng của lò xo (đơn vị: Newton trên mét, N/m).
- \(\Delta x\) là độ biến dạng của lò xo so với vị trí cân bằng (đơn vị: mét, m).
Quy trình giải bài tập cụ thể như sau:
- Xác định độ cứng \(k\) của lò xo từ đề bài.
- Đo hoặc tính toán độ biến dạng \(\Delta x\) của lò xo khi bị kéo hoặc nén.
- Thay giá trị \(k\) và \(\Delta x\) vào công thức \(F = -k \Delta x\) để tính lực đàn hồi \(F\).
- Viết kết luận về lực đàn hồi của lò xo.
Ví dụ:
Một lò xo có độ cứng \(k = 100 \, \text{N/m}\) bị kéo dãn \( \Delta x = 0,05 \, \text{m}\). Tính lực đàn hồi của lò xo.
- Bước 1: Xác định độ cứng \(k = 100 \, \text{N/m}\).
- Bước 2: Xác định độ biến dạng \(\Delta x = 0,05 \, \text{m}\).
- Bước 3: Thay vào công thức: \[ F = -100 \times 0,05 = -5 \, \text{N} \]
- Bước 4: Kết luận: Lực đàn hồi của lò xo là \(5 \, \text{N}\) và ngược chiều với hướng kéo.
XEM THÊM:
Bài tập Lý 2: Phân tích chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động có quãng đường đi được luôn tỉ lệ thuận với thời gian chuyển động. Để phân tích chuyển động thẳng đều, chúng ta sẽ sử dụng các công thức cơ bản sau:
Công thức cơ bản:
Quãng đường \(s\) được tính bằng công thức:
\[ s = v \times t \]
Trong đó:
- \(s\) là quãng đường (m)
- \(v\) là vận tốc (m/s)
- \(t\) là thời gian chuyển động (s)
Ví dụ cụ thể:
Giả sử một xe máy chuyển động thẳng đều với vận tốc \(v = 20 \, \text{m/s}\). Tính quãng đường đi được sau \(t = 5 \, \text{s}\).
Áp dụng công thức, ta có:
\[ s = v \times t = 20 \, \text{m/s} \times 5 \, \text{s} = 100 \, \text{m} \]
Vậy, quãng đường xe máy đi được là 100 mét.
Phân tích đồ thị:
Trong chuyển động thẳng đều, đồ thị biểu diễn quãng đường theo thời gian là một đường thẳng có độ dốc bằng vận tốc \(v\). Đồ thị này cho phép ta dễ dàng xác định quãng đường hoặc thời gian khi biết một trong hai yếu tố còn lại.
Những lưu ý khi phân tích chuyển động thẳng đều:
- Vận tốc là hằng số, không đổi theo thời gian.
- Quãng đường đi được trong những khoảng thời gian bằng nhau luôn bằng nhau.
- Chuyển động thẳng đều không có gia tốc (a = 0).
Bài tập vận dụng:
1. Một ô tô chạy với vận tốc \(v = 60 \, \text{km/h}\) trong thời gian \(t = 2 \, \text{h}\). Hãy tính quãng đường mà ô tô đã đi được.
2. Từ đồ thị biểu diễn quãng đường \(s\) theo thời gian \(t\) của một vật chuyển động thẳng đều, hãy xác định vận tốc của vật đó.
Những bài tập trên giúp chúng ta củng cố kiến thức về chuyển động thẳng đều và khả năng phân tích các yếu tố ảnh hưởng đến chuyển động.

Bài tập Tiếng Anh 1: Chia thì đúng trong câu
Trong bài tập này, các em sẽ rèn luyện kỹ năng chia thì của động từ trong câu Tiếng Anh. Dựa trên tình hình thực tế và cách diễn đạt, các em cần lựa chọn thì phù hợp để hoàn thành các câu dưới đây.
Bài tập
-
Hiện tại, Đội tuyển bóng đá nữ Việt Nam (to play) rất nhiều trận đấu quốc tế. Hãy chia động từ to play ở thì hiện tại tiếp diễn.
-
Ngày hôm qua, đội tuyển đã (to win) một trận đấu quan trọng. Hãy chia động từ to win ở thì quá khứ đơn.
-
Đội tuyển nữ Nhật Bản (to score) nhiều bàn thắng trong trận đấu gần đây. Hãy chia động từ to score ở thì hiện tại hoàn thành.
-
Ngày mai, đội tuyển nữ sẽ (to face) đối thủ Nepal. Hãy chia động từ to face ở thì tương lai đơn.
Đáp án
-
Câu 1: Đội tuyển bóng đá nữ Việt Nam is playing rất nhiều trận đấu quốc tế.
-
Câu 2: Đội tuyển đã won một trận đấu quan trọng ngày hôm qua.
-
Câu 3: Đội tuyển nữ Nhật Bản has scored nhiều bàn thắng trong trận đấu gần đây.
-
Câu 4: Đội tuyển nữ sẽ face đối thủ Nepal ngày mai.
Chúc các em học tốt và nắm vững kiến thức về thì trong Tiếng Anh!

Bài tập Tiếng Anh 2: Chọn từ đúng điền vào chỗ trống
Để giúp học sinh lớp 1 nâng cao kỹ năng chọn từ đúng trong câu tiếng Anh, bài tập này được thiết kế với nhiều dạng câu hỏi khác nhau, từ dễ đến khó. Những câu hỏi này không chỉ kiểm tra kiến thức ngữ pháp cơ bản mà còn khuyến khích các em sử dụng ngôn ngữ một cách linh hoạt và tự tin hơn.
Bài tập 1: Điền từ đúng vào chỗ trống trong các câu sau:
- She ______ (go/goes) to school every day.
- They ______ (is/are) playing football now.
- My brother ______ (like/likes) to eat apples.
- We ______ (watch/watching) TV at the moment.
- I ______ (am/are) a student.
Bài tập 2: Điền từ phù hợp với ngữ cảnh:
- She ______ (is/are) a good girl.
- He ______ (has/have) two dogs.
- They ______ (like/likes) to swim in the pool.
- My father ______ (work/works) in a factory.
- The cats ______ (is/are) under the table.
Bài tập 3: Chọn từ đúng điền vào chỗ trống và giải thích lý do tại sao:
- The sun ______ (shine/shines) brightly in the sky.
- She ______ (don't/doesn't) like to eat vegetables.
- We ______ (isn't/aren't) going to the park today.
- The dog ______ (bark/barks) loudly at night.
- They ______ (was/were) at home yesterday.
Những bài tập trên không chỉ giúp các em nhận biết từ ngữ và ngữ pháp đúng mà còn khuyến khích việc thực hành thường xuyên, giúp các em tự tin hơn trong việc sử dụng tiếng Anh trong giao tiếp hàng ngày.
Bài tập Toán 3: Tính thể tích hình lập phương
Trong bài tập này, các em sẽ học cách tính thể tích của một hình lập phương. Đây là một bài toán đơn giản nhưng rất quan trọng trong việc rèn luyện khả năng tư duy không gian của các em. Chúng ta sẽ đi từng bước để hiểu rõ cách giải.
1. Công thức tính thể tích hình lập phương
Hình lập phương là một khối hình học có tất cả các cạnh bằng nhau. Để tính thể tích hình lập phương, chúng ta sử dụng công thức:
\[ V = a^3 \]
Trong đó:
- \( V \) là thể tích của hình lập phương.
- \( a \) là độ dài một cạnh của hình lập phương.
2. Ví dụ
Giả sử chúng ta có một hình lập phương với cạnh dài 3 cm. Hãy tính thể tích của nó:
Áp dụng công thức:
\[ V = 3^3 = 27 \, \text{cm}^3 \]
Vậy thể tích của hình lập phương là 27 cm3.
3. Bài tập thực hành
Các em hãy làm các bài tập sau đây để rèn luyện thêm:
- Tính thể tích của hình lập phương có cạnh dài 5 cm.
- Một hình lập phương có thể tích là 64 cm3. Hãy tìm độ dài cạnh của nó.
- Tính thể tích của một hình lập phương có cạnh dài gấp đôi cạnh của một hình lập phương có cạnh 4 cm.
4. Đáp án
| Bài 1: | \( V = 5^3 = 125 \, \text{cm}^3 \) |
| Bài 2: | \( a = \sqrt[3]{64} = 4 \, \text{cm} \) |
| Bài 3: | Thể tích hình lập phương mới: \( V = (2 \times 4)^3 = 512 \, \text{cm}^3 \) |
Các em hãy kiểm tra lại kết quả của mình với đáp án và hiểu rõ từng bước giải nhé. Học tốt!

Bài tập Lý 3: Phân tích lực tác dụng lên vật chuyển động
Trong bài tập này, chúng ta sẽ tìm hiểu và phân tích các lực tác dụng lên một vật đang chuyển động. Vật chuyển động có thể chịu ảnh hưởng từ nhiều loại lực khác nhau, và việc phân tích các lực này là bước quan trọng để hiểu rõ hơn về cơ chế chuyển động của vật.
1. Xác định các lực tác dụng lên vật
- Lực hấp dẫn \((F_g)\): Đây là lực mà Trái Đất tác dụng lên vật, kéo vật về phía tâm của hành tinh. Độ lớn của lực này được tính bằng công thức \[ F_g = m \cdot g \], trong đó \(m\) là khối lượng của vật và \(g\) là gia tốc trọng trường (thường là 9,8 m/s²).
- Lực cản không khí \((F_{cản})\): Lực này tác dụng ngược chiều chuyển động của vật, làm giảm tốc độ của vật. Độ lớn của lực này phụ thuộc vào diện tích bề mặt tiếp xúc của vật, vận tốc chuyển động và mật độ không khí.
- Lực ma sát \((F_{ma sát})\): Lực này cũng tác dụng ngược chiều với chuyển động của vật khi vật tiếp xúc với một bề mặt khác, cản trở sự trượt của vật trên bề mặt đó. Công thức tính lực ma sát là \[ F_{ma sát} = \mu \cdot F_n \], trong đó \(\mu\) là hệ số ma sát và \(F_n\) là lực pháp tuyến.
2. Phân tích cân bằng lực
Khi một vật chuyển động đều, nghĩa là không thay đổi vận tốc, tổng các lực tác dụng lên vật phải bằng không. Điều này được thể hiện qua phương trình cân bằng lực:
Nếu vật chuyển động nhanh dần đều, nghĩa là tổng lực tác dụng lên vật không bằng không và theo định luật Newton II:
Trong đó \(m\) là khối lượng của vật và \(\vec{a}\) là gia tốc của vật.
3. Ví dụ thực hành
Xét một ô tô đang chuyển động trên đường phẳng với vận tốc không đổi. Các lực tác dụng lên ô tô bao gồm lực kéo do động cơ tạo ra, lực cản của không khí và lực ma sát giữa lốp xe và mặt đường. Hãy phân tích các lực này và xác định điều kiện để ô tô chuyển động đều.
Giả sử lực kéo \(F_k\) từ động cơ, lực cản không khí \(F_{cản}\), và lực ma sát \(F_{ma sát}\) đã được tính toán trước đó. Điều kiện để ô tô chuyển động đều là:
Nếu lực kéo lớn hơn tổng lực cản và lực ma sát, ô tô sẽ tăng tốc; ngược lại, nếu nhỏ hơn, ô tô sẽ giảm tốc.
4. Bài tập tự giải
- Một vật có khối lượng 5 kg đang trượt trên mặt phẳng ngang với hệ số ma sát \(\mu = 0,3\). Hãy tính lực ma sát tác dụng lên vật.
- Giả sử vật trên đang bị tác dụng bởi một lực kéo 20 N theo phương ngang. Xác định gia tốc của vật.
- Hãy phân tích lực tác dụng lên một quả bóng đang rơi tự do từ độ cao 10 m.
Bài tập Tiếng Anh 3: Viết lại câu sử dụng cấu trúc khác
Dưới đây là một số bài tập giúp học sinh lớp 3 luyện tập kỹ năng viết lại câu sử dụng các cấu trúc ngữ pháp khác nhau. Hãy cùng bắt đầu!
-
Bài tập 1: Chuyển các câu sau sang dạng phủ định.
- \(\text{She is reading a book.}\) ⟶ \(\text{She is not reading a book.}\)
- \(\text{They are playing soccer.}\) ⟶ \(\text{They are not playing soccer.}\)
- \(\text{He likes ice cream.}\) ⟶ \(\text{He does not like ice cream.}\)
-
Bài tập 2: Viết lại câu sử dụng "because".
- \(\text{She was tired, so she went to bed early.}\) ⟶ \(\text{She went to bed early because she was tired.}\)
- \(\text{It was raining, so they stayed inside.}\) ⟶ \(\text{They stayed inside because it was raining.}\)
-
Bài tập 3: Sử dụng "although" để kết hợp hai câu sau.
- \(\text{The weather was cold. They went for a walk.}\) ⟶ \(\text{Although the weather was cold, they went for a walk.}\)
- \(\text{She was sick. She went to school.}\) ⟶ \(\text{Although she was sick, she went to school.}\)
-
Bài tập 4: Chuyển các câu sau sang câu hỏi.
- \(\text{They are cooking dinner.}\) ⟶ \(\text{Are they cooking dinner?}\)
- \(\text{You like apples.}\) ⟶ \(\text{Do you like apples?}\)
- \(\text{She can swim.}\) ⟶ \(\text{Can she swim?}\)
Hãy thực hành thường xuyên để nắm vững các cấu trúc này nhé!
Bài tập Toán 4: Giải hệ phương trình tuyến tính
Trong bài tập này, chúng ta sẽ cùng nhau giải quyết một hệ phương trình tuyến tính cơ bản. Hệ phương trình tuyến tính là một tập hợp các phương trình trong đó mỗi phương trình có dạng tuyến tính. Bài tập này sẽ giúp các em hiểu rõ hơn về cách giải hệ phương trình tuyến tính thông qua các bước cụ thể.
Bước 1: Đặt hệ phương trình
Giả sử chúng ta có hệ phương trình tuyến tính hai ẩn:
Trong đó, \(a\), \(b\), \(c\), \(d\), \(e\), và \(f\) là các hằng số đã cho.
Bước 2: Sử dụng phương pháp thế hoặc cộng đại số
- Phương pháp thế: Giải một trong hai phương trình để tìm một ẩn, sau đó thế giá trị vừa tìm được vào phương trình còn lại.
- Phương pháp cộng đại số: Nhân hai phương trình với các hệ số thích hợp để loại bỏ một ẩn, sau đó giải phương trình còn lại.
Bước 3: Giải phương trình sau khi đã loại bỏ một ẩn
Sau khi đã loại bỏ một ẩn, chúng ta sẽ có một phương trình với một ẩn duy nhất. Giải phương trình này để tìm giá trị của ẩn còn lại.
Bước 4: Tìm giá trị của ẩn còn lại
Dùng giá trị vừa tìm được thế vào một trong các phương trình ban đầu để tìm giá trị của ẩn còn lại.
Bước 5: Kết luận
Ghi lại kết quả của hai ẩn số \(x\) và \(y\). Đây là nghiệm của hệ phương trình tuyến tính đã cho.
Ví dụ:
Xét hệ phương trình:
Chúng ta sẽ thực hiện các bước trên để tìm giá trị của \(x\) và \(y\).
Với cách tiếp cận này, các em sẽ dễ dàng hiểu và giải được các hệ phương trình tuyến tính cơ bản. Hãy cùng thực hành nhiều hơn để nắm vững kỹ năng này!