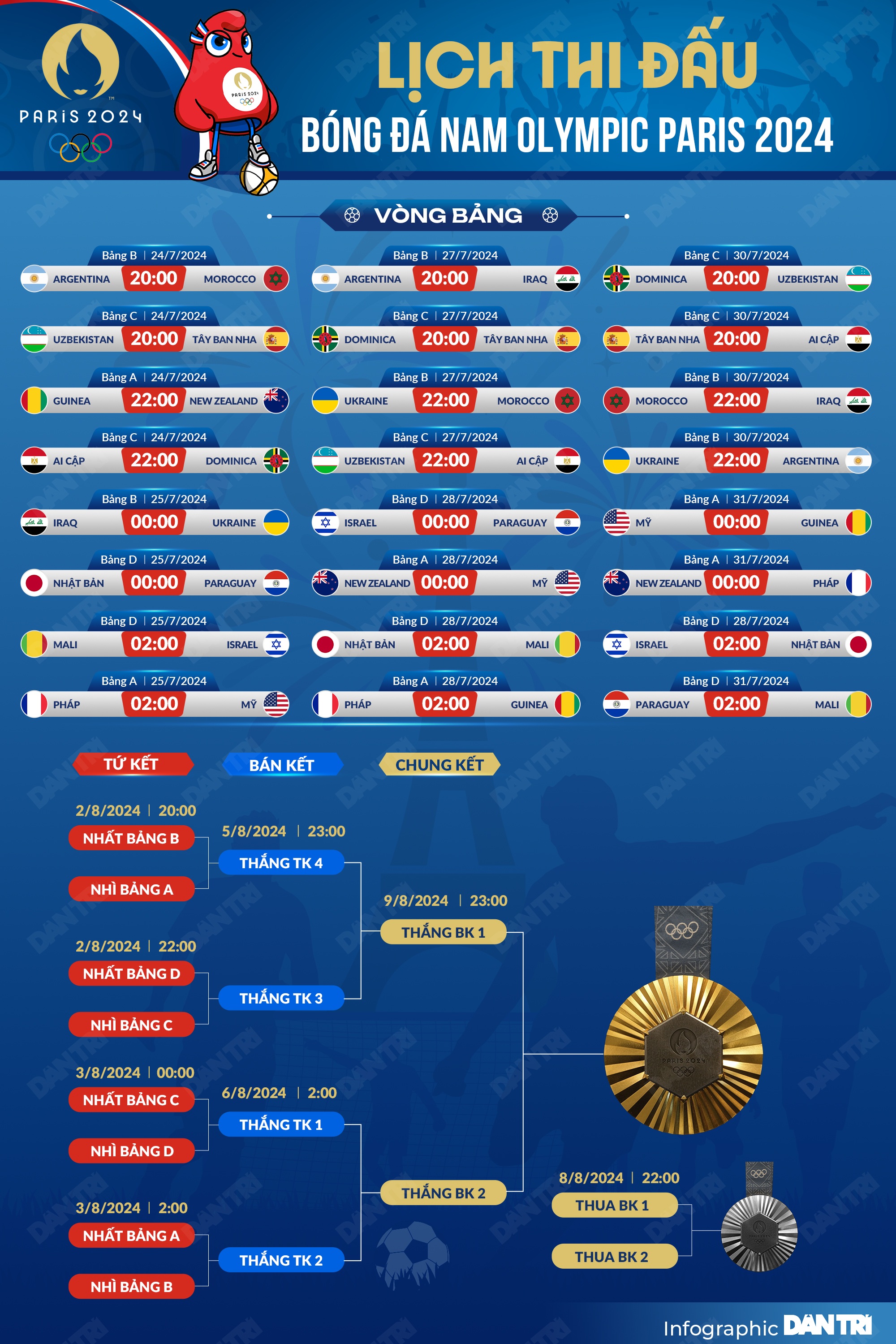
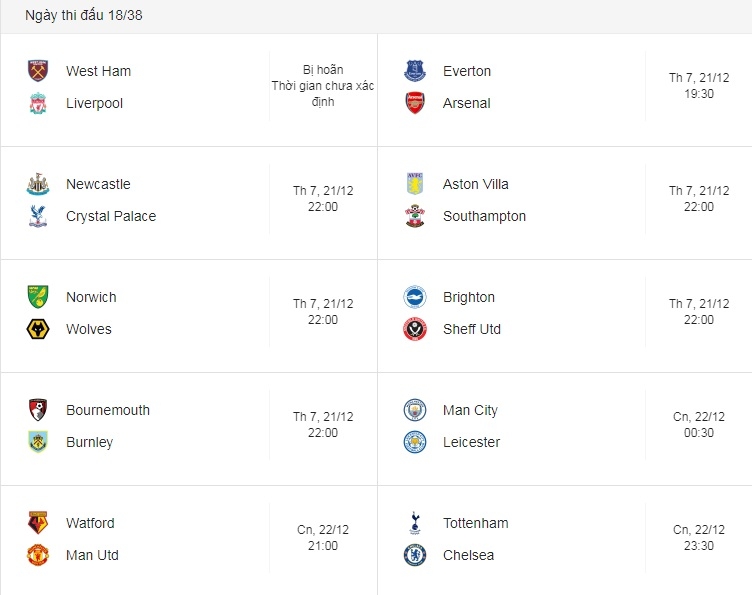
Chủ đề lịch thi đấu bóng đá cúp c1 đêm nay: Lịch thi đấu bóng đá Cúp C1 đêm nay cập nhật chi tiết từng trận đấu, thời gian, và kênh truyền hình trực tiếp. Đừng bỏ lỡ cơ hội theo dõi những trận cầu đỉnh cao và cổ vũ cho đội bóng yêu thích của bạn. Cùng khám phá mọi thông tin cần thiết để không bỏ lỡ giây phút nào của giải đấu danh giá này.
Mục lục
- Lịch Thi Đấu Bóng Đá Cúp C1 Đêm Nay
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Có Lời Giải (Chủ đề Toán Học)
- Bài Tập 1: Phương Trình Bậc Hai
- Bài Tập 2: Hệ Phương Trình Tuyến Tính
- Bài Tập 3: Tính Đạo Hàm Của Hàm Số
- Bài Tập 4: Tích Phân Bất Định
- Bài Tập 5: Dãy Số Và Chuỗi Số
- Bài Tập 6: Hình Học Không Gian
- Bài Tập 7: Xác Suất Và Thống Kê
- Bài Tập 8: Phương Trình Vi Phân
- Bài Tập 9: Hình Học Giải Tích
- Bài Tập 10: Bất Đẳng Thức Và Bất Phương Trình
Lịch Thi Đấu Bóng Đá Cúp C1 Đêm Nay
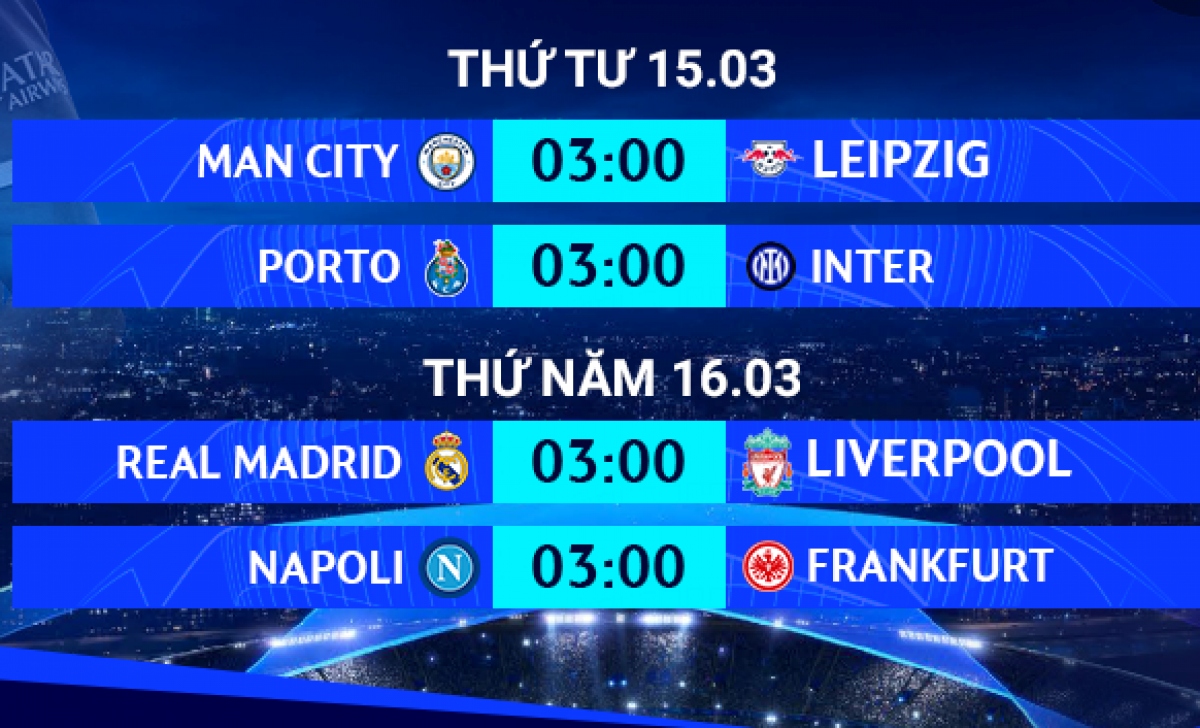
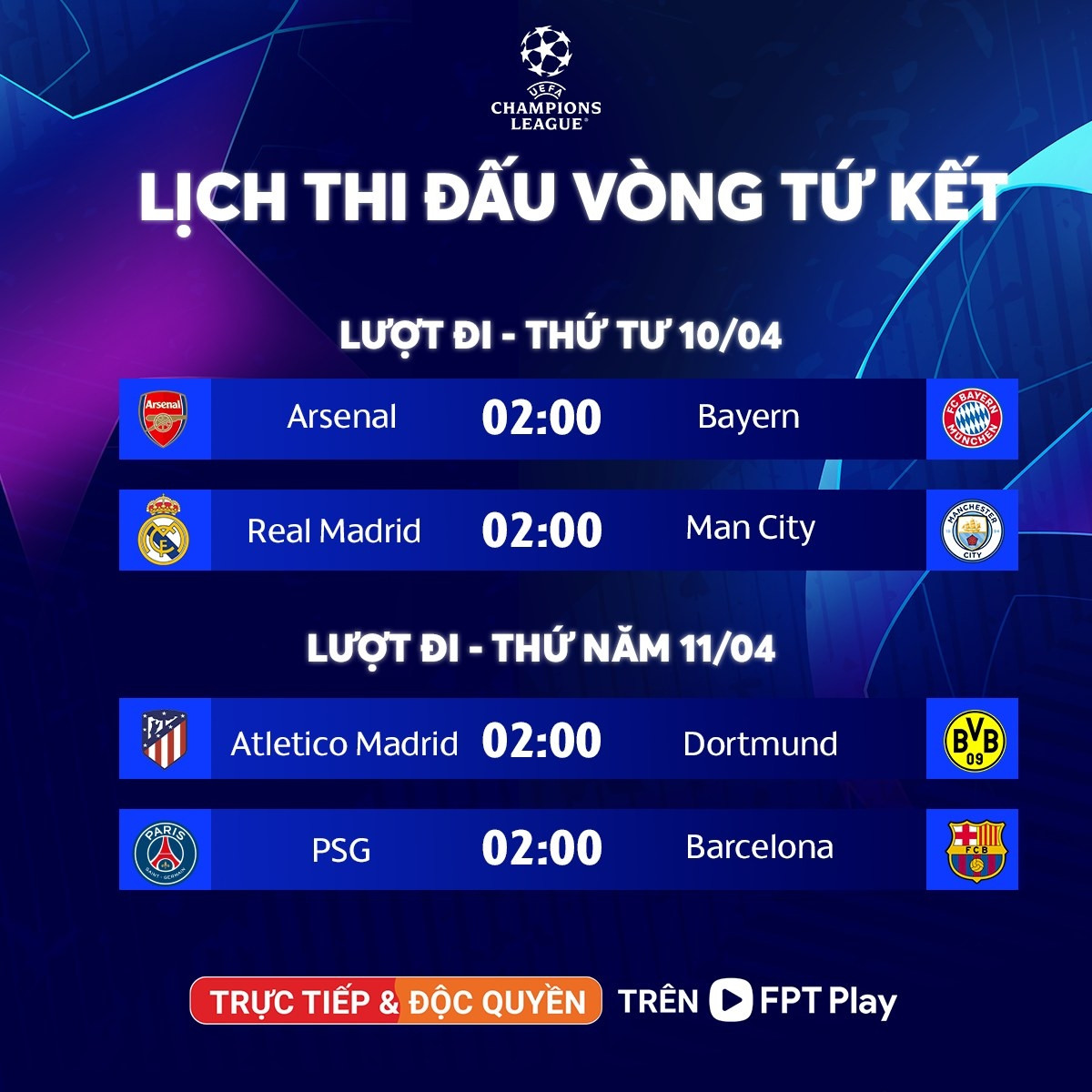
Dưới đây là lịch thi đấu các trận đấu Cúp C1 châu Âu diễn ra vào đêm nay, hứa hẹn mang đến những trận cầu kịch tính và đầy hấp dẫn.
Lịch Thi Đấu Vòng Play-off
- 2h00 sáng 22/08/2024: Young Boys vs Galatasaray
- 2h00 sáng 22/08/2024: Midtjylland vs Slovan Bratislava
- 2h00 sáng 22/08/2024: Malmö vs Sparta Prague
- 2h00 sáng 22/08/2024: Dinamo Kiev vs Salzburg
Lịch Thi Đấu Cúp C1 Đông Nam Á
- 18h00: Thanh Hóa vs Shan United
- 18h30: PSM Makassar vs BG Pathum United
- 20h00: Terengganu vs Svay Rieng
Các Trận Đấu Khác
Cùng với các trận đấu Cúp C1, các giải đấu khác như U20 Nam Á, Cúp C3 châu Âu, và các giải đấu cấp CLB khu vực CONCACAF cũng sẽ diễn ra trong đêm nay.
Đừng bỏ lỡ bất kỳ trận đấu nào, hãy cập nhật liên tục để theo dõi diễn biến các trận đấu mà bạn yêu thích.
.png)
Mục Lục Tổng Hợp
- Lịch Thi Đấu Bóng Đá Cúp C1 Đêm Nay:
- Danh sách các trận đấu diễn ra trong đêm nay.
- Thời gian và địa điểm diễn ra các trận đấu.
- Kênh truyền hình trực tiếp các trận đấu.
- Phân tích và dự đoán kết quả các trận đấu.
- Kết Quả Thi Đấu Cúp C1 Đêm Qua:
- Thống kê kết quả các trận đấu đã diễn ra.
- Bảng xếp hạng sau loạt trận đêm qua.
- Các bàn thắng đẹp và những khoảnh khắc nổi bật.
- Nhận Định Và Dự Đoán Các Trận Đấu Cúp C1:
- Phân tích chuyên sâu từng cặp đấu.
- Dự đoán kết quả dựa trên phong độ và lịch sử đối đầu.
- Ý kiến chuyên gia và người hâm mộ.
- Cập Nhật Tin Tức Liên Quan Đến Cúp C1:
- Tin tức mới nhất về các đội bóng và cầu thủ.
- Những thay đổi trong danh sách thi đấu và chấn thương.
- Phỏng vấn HLV và cầu thủ trước và sau trận đấu.
- Thông Tin Về Giải Đấu Và Lịch Sử Cúp C1:
- Lịch sử hình thành và phát triển của Cúp C1.
- Thành tích các đội bóng qua các mùa giải.
- Những kỷ lục và sự kiện đáng nhớ trong lịch sử giải đấu.
10 Dạng Bài Tập Có Lời Giải (Chủ đề Toán Học)
- Bài Tập 1: Phương Trình Bậc Hai
Giải và phân tích các nghiệm của phương trình bậc hai \[ ax^2 + bx + c = 0 \]. Tìm các điều kiện để phương trình có nghiệm thực, nghiệm kép hoặc vô nghiệm.
- Bài Tập 2: Hệ Phương Trình Tuyến Tính
Giải hệ phương trình tuyến tính hai hoặc ba ẩn số bằng phương pháp cộng đại số hoặc ma trận. Ví dụ: Giải hệ \[ \begin{cases} ax + by = c \\ dx + ey = f \end{cases} \].
- Bài Tập 3: Tính Đạo Hàm Của Hàm Số
Tìm đạo hàm của các hàm số đơn giản và phức tạp. Ví dụ: Tính \(\frac{d}{dx}(x^3 - 5x^2 + 4x - 7)\).
- Bài Tập 4: Tích Phân Bất Định
Tính tích phân bất định của các hàm số. Ví dụ: Tính \(\int (3x^2 - 2x + 1) \, dx\).
- Bài Tập 5: Dãy Số Và Chuỗi Số
Tìm số hạng tổng quát, tổng của dãy số và kiểm tra tính hội tụ của chuỗi số. Ví dụ: Tìm tổng của dãy số \(\sum_{n=1}^{\infty} \frac{1}{n^2}\).
- Bài Tập 6: Hình Học Không Gian
Giải các bài toán về thể tích, diện tích của các hình khối trong không gian ba chiều. Ví dụ: Tính thể tích của khối lập phương có cạnh dài \(a\).
- Bài Tập 7: Xác Suất Và Thống Kê
Tính xác suất của các biến cố, phân phối xác suất và các bài toán thống kê cơ bản. Ví dụ: Tính xác suất để một con xúc xắc ra mặt có số chẵn.
- Bài Tập 8: Phương Trình Vi Phân
Giải các phương trình vi phân bậc nhất và bậc hai. Ví dụ: Giải phương trình vi phân \(\frac{dy}{dx} + P(x)y = Q(x)\).
- Bài Tập 9: Hình Học Giải Tích
Giải các bài toán liên quan đến đường thẳng, đường tròn và mặt phẳng trong không gian. Ví dụ: Tìm phương trình đường thẳng đi qua hai điểm \(A(x_1, y_1)\) và \(B(x_2, y_2)\).
- Bài Tập 10: Bất Đẳng Thức Và Bất Phương Trình
Chứng minh các bất đẳng thức và giải các bất phương trình. Ví dụ: Chứng minh bất đẳng thức \[a^2 + b^2 \geq 2ab\].

Bài Tập 1: Phương Trình Bậc Hai
Phương trình bậc hai là dạng phương trình có dạng tổng quát:
\[ ax^2 + bx + c = 0 \]
Trong đó \(a\), \(b\), \(c\) là các hệ số, với \(a \neq 0\). Giải phương trình bậc hai thường bao gồm các bước sau:
- Tính biệt thức \(\Delta\):
Biệt thức \(\Delta\) được tính bằng công thức:
\[ \Delta = b^2 - 4ac \]
- Xét dấu của \(\Delta\):
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt:
- Nếu \(\Delta = 0\), phương trình có nghiệm kép:
- Nếu \(\Delta < 0\), phương trình vô nghiệm thực.
\[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
\[ x = \frac{-b}{2a} \]
- Viết kết luận:
Dựa trên giá trị của \(\Delta\), kết luận về số nghiệm của phương trình và giá trị của chúng (nếu có).
Ví dụ: Giải phương trình bậc hai \[ 2x^2 - 4x + 2 = 0 \].
Bước 1: Tính \(\Delta\): \[ \Delta = (-4)^2 - 4 \cdot 2 \cdot 2 = 16 - 16 = 0 \]
Bước 2: Vì \(\Delta = 0\), phương trình có nghiệm kép:
\[ x = \frac{-(-4)}{2 \cdot 2} = \frac{4}{4} = 1 \]
Kết luận: Phương trình có nghiệm kép \(x = 1\).

Bài Tập 2: Hệ Phương Trình Tuyến Tính
Trong toán học, hệ phương trình tuyến tính là một tập hợp các phương trình tuyến tính mà chúng ta cần tìm nghiệm thỏa mãn tất cả các phương trình trong hệ. Đây là một khái niệm cơ bản và quan trọng, thường được sử dụng trong nhiều lĩnh vực như kỹ thuật, kinh tế, và khoa học máy tính.
1. Định Nghĩa Hệ Phương Trình Tuyến Tính
Một hệ phương trình tuyến tính gồm \(n\) phương trình với \(m\) ẩn số có dạng tổng quát như sau:
Trong đó:
- \(a_{ij}\) là các hệ số của hệ phương trình (với \(i = 1, 2, \dots, n\) và \(j = 1, 2, \dots, m\)).
- \(x_j\) là các ẩn số.
- \(b_i\) là các hằng số tương ứng với mỗi phương trình.
2. Phương Pháp Giải Hệ Phương Trình Tuyến Tính
2.1. Phương Pháp Thế
Đây là phương pháp đơn giản nhất, thường được sử dụng khi hệ phương trình có hai hoặc ba phương trình. Các bước thực hiện như sau:
- Chọn một phương trình từ hệ và giải nó theo một ẩn số.
- Thay biểu thức của ẩn số vừa tìm được vào các phương trình còn lại.
- Tiếp tục giải hệ cho đến khi tìm được nghiệm cho tất cả các ẩn số.
2.2. Phương Pháp Cramer
Phương pháp này áp dụng cho hệ phương trình có số phương trình bằng với số ẩn số (\(n = m\)) và ma trận hệ số có định thức khác không. Các bước thực hiện như sau:
- Tính định thức của ma trận hệ số \(D\).
- Tính các định thức con \(D_j\) bằng cách thay cột thứ \(j\) của ma trận hệ số bằng cột hệ số tự do \(b\).
- Nghiệm của hệ phương trình là \(x_j = \frac{D_j}{D}\).
2.3. Phương Pháp Gauss
Đây là phương pháp sử dụng phổ biến trong máy tính để giải các hệ phương trình lớn. Các bước thực hiện bao gồm:
- Chuyển hệ phương trình về dạng bậc thang bằng cách sử dụng các phép biến đổi sơ cấp trên hàng.
- Giải hệ phương trình từ phương trình bậc thấp nhất.
- Sử dụng phép thế ngược để tìm các ẩn số còn lại.
3. Ứng Dụng Của Hệ Phương Trình Tuyến Tính
Hệ phương trình tuyến tính có ứng dụng rộng rãi trong nhiều lĩnh vực như:
- Giải quyết các vấn đề tối ưu hóa trong kinh tế và quản lý.
- Phân tích mạng điện trong kỹ thuật điện.
- Mô hình hóa các hệ thống động học trong khoa học tự nhiên.
4. Ví Dụ Minh Họa
Giả sử chúng ta có hệ phương trình tuyến tính sau:
Chúng ta sẽ giải hệ này bằng phương pháp thế:
- Giải phương trình thứ hai theo \(y\): \(y = 4x - 1\).
- Thay vào phương trình thứ nhất: \(2x + 3(4x - 1) = 5\).
- Giải để tìm \(x\), sau đó thay ngược lại để tìm \(y\).
Kết quả là: \(x = 1\), \(y = 3\).
5. Bài Tập Tự Giải
Giải hệ phương trình tuyến tính sau bằng phương pháp Gauss:
Hãy thử giải và kiểm tra kết quả!

Bài Tập 3: Tính Đạo Hàm Của Hàm Số
Đạo hàm của hàm số là một khái niệm cơ bản và quan trọng trong giải tích. Việc tính đạo hàm giúp chúng ta hiểu rõ hơn về tốc độ thay đổi của hàm số, cũng như ứng dụng trong nhiều lĩnh vực khác nhau như vật lý, kinh tế và kỹ thuật.
Công Thức Tính Đạo Hàm
- Đạo hàm của hàm số \( f(x) \) tại điểm \( x \) được định nghĩa bởi giới hạn:
\[
f'(x) = \lim_{{h \to 0}} \frac{{f(x+h) - f(x)}}{h}
\]
- Một số quy tắc cơ bản để tính đạo hàm:
- Đạo hàm của hằng số: \( (C)' = 0 \).
- Đạo hàm của hàm số mũ: \( (e^x)' = e^x \).
- Đạo hàm của hàm lũy thừa: \( (x^n)' = n \cdot x^{n-1} \).
- Đạo hàm của hàm số lượng giác: \( (\sin x)' = \cos x \) và \( (\cos x)' = -\sin x \).
- Quy tắc nhân: \( (u \cdot v)' = u' \cdot v + u \cdot v' \).
- Quy tắc chia: \( \left(\frac{u}{v}\right)' = \frac{u' \cdot v - u \cdot v'}{v^2} \).
Ví Dụ Cụ Thể
Hãy tính đạo hàm của hàm số sau:
\[
f(x) = 3x^4 - 5x^2 + 2x - 7
\]
- Bước 1: Sử dụng quy tắc đạo hàm của từng thành phần.
- Bước 2: Áp dụng công thức tổng quát để tính đạo hàm của hàm số trên.
Ta có:
\[
f'(x) = 12x^3 - 10x + 2
\]
Ứng Dụng Thực Tế
Đạo hàm không chỉ là một công cụ toán học mà còn có nhiều ứng dụng trong đời sống thực tế, ví dụ:
- Trong vật lý, đạo hàm của quãng đường theo thời gian cho ta vận tốc.
- Trong kinh tế, đạo hàm của lợi nhuận theo sản lượng giúp xác định mức sản xuất tối ưu.
- Trong kỹ thuật, đạo hàm giúp xác định tốc độ thay đổi của các thông số quan trọng trong quá trình sản xuất.
Việc nắm vững kỹ thuật tính đạo hàm sẽ giúp các bạn giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.
XEM THÊM:
Bài Tập 4: Tích Phân Bất Định
Tích phân bất định là một trong những khái niệm cơ bản trong giải tích, được sử dụng để tìm hàm nguyên hàm của một hàm số đã cho. Dưới đây là hướng dẫn chi tiết cách giải một số bài tập liên quan đến tích phân bất định.
-
Bài Tập 1: Tìm nguyên hàm của hàm số \(f(x) = 2x + 3\)
Để tìm nguyên hàm của hàm số \(f(x) = 2x + 3\), ta thực hiện các bước sau:
- Bước 1: Xác định nguyên hàm của từng hạng tử.
- \(\int 2x \, dx = x^2 + C_1\)
- \(\int 3 \, dx = 3x + C_2\)
- Bước 2: Tổng hợp các kết quả lại để tìm nguyên hàm chung: \[ F(x) = x^2 + 3x + C \] Trong đó, \(C = C_1 + C_2\) là hằng số tùy ý.
- Bước 1: Xác định nguyên hàm của từng hạng tử.
-
Bài Tập 2: Tìm nguyên hàm của hàm số \(g(x) = \frac{1}{x}\)
Đối với hàm số \(g(x) = \frac{1}{x}\), ta có thể tìm nguyên hàm như sau:
- Bước 1: Áp dụng công thức nguyên hàm cơ bản: \[ \int \frac{1}{x} \, dx = \ln |x| + C \]
- Bước 2: Kết luận kết quả: \[ G(x) = \ln |x| + C \]
-
Bài Tập 3: Tìm nguyên hàm của hàm số \(h(x) = e^x\)
Nguyên hàm của hàm số mũ cơ bản \(h(x) = e^x\) được tìm như sau:
- Bước 1: Áp dụng công thức nguyên hàm cho hàm số mũ: \[ \int e^x \, dx = e^x + C \]
- Bước 2: Kết luận kết quả: \[ H(x) = e^x + C \]
-
Bài Tập 4: Tìm nguyên hàm của hàm số \(k(x) = \sin(x)\)
Để tìm nguyên hàm của hàm số \(k(x) = \sin(x)\), ta thực hiện như sau:
- Bước 1: Áp dụng công thức nguyên hàm cơ bản của hàm số lượng giác: \[ \int \sin(x) \, dx = -\cos(x) + C \]
- Bước 2: Kết luận kết quả: \[ K(x) = -\cos(x) + C \]
Như vậy, việc tìm nguyên hàm cho các hàm số cơ bản có thể được thực hiện một cách tuần tự bằng cách áp dụng các công thức nguyên hàm tương ứng.
Bài Tập 5: Dãy Số Và Chuỗi Số
Trong bài tập này, chúng ta sẽ tìm hiểu về dãy số và chuỗi số, hai khái niệm cơ bản trong toán học đại số. Đây là nền tảng để giải quyết các bài toán phức tạp hơn trong giải tích và toán học ứng dụng.
I. Dãy Số
Một dãy số là một danh sách các số được sắp xếp theo thứ tự nhất định, thường là theo thứ tự tăng dần hoặc giảm dần. Các phần tử của dãy được kí hiệu bởi \(a_n\), trong đó \(n\) là chỉ số của phần tử trong dãy.
- Ví dụ 1: Dãy số tự nhiên: \(1, 2, 3, 4, \dots\)
- Ví dụ 2: Dãy số hình học với công bội \(r = 2\): \(1, 2, 4, 8, 16, \dots\)
Một dãy số có thể hội tụ hoặc phân kì. Để xác định tính hội tụ, ta cần tính giới hạn của dãy số khi \(n\) tiến tới vô cùng.
- Giới hạn của dãy: \(\lim_{{n \to \infty}} a_n = L\)
- Nếu giới hạn \(L\) tồn tại và là một số hữu hạn, dãy số được gọi là hội tụ.
- Nếu giới hạn không tồn tại hoặc là vô cùng, dãy số được gọi là phân kì.
II. Chuỗi Số
Chuỗi số là tổng của các phần tử trong một dãy số. Nếu dãy số \(a_n\) có giới hạn hội tụ, thì chuỗi số tương ứng cũng có thể hội tụ.
Chuỗi số thường được kí hiệu bởi:
Một số loại chuỗi đặc biệt:
- Chuỗi số học: \(S_n = \sum_{n=1}^{N} n = \frac{N(N+1)}{2}\)
- Chuỗi hình học: \(S = \sum_{n=0}^{\infty} r^n = \frac{1}{1-r} \quad \text{khi} \ |r| < 1\)
III. Bài Tập Mẫu
- Tìm giới hạn của dãy số \(a_n = \frac{1}{n}\) khi \(n\) tiến tới vô cùng.
- Tính tổng của chuỗi số hình học với \(r = \frac{1}{2}\).
- Kiểm tra tính hội tụ của chuỗi số \(S = \sum_{n=1}^{\infty} \frac{1}{n^2}\).
IV. Ứng Dụng Thực Tế
Trong thực tế, dãy số và chuỗi số được ứng dụng rộng rãi trong các lĩnh vực như tài chính, khoa học dữ liệu, và kỹ thuật. Ví dụ, chuỗi số được sử dụng để mô hình hóa sự tăng trưởng của quỹ đầu tư hoặc dự đoán xu hướng thị trường.

Bài Tập 6: Hình Học Không Gian
Hình học không gian là một phần quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về các đối tượng ba chiều như hình lăng trụ, hình chóp, hình cầu, hình nón, và hình trụ. Bài tập này sẽ giúp bạn làm quen với các khái niệm cơ bản, các công thức tính thể tích, diện tích bề mặt và cách áp dụng chúng vào thực tế.
1. Công Thức Cơ Bản
- Thể tích hình hộp chữ nhật: \[ V = a \times b \times c \] với \( a, b, c \) là các kích thước của hình hộp.
- Thể tích hình lăng trụ: \[ V = S_{đáy} \times h \] với \( S_{đáy} \) là diện tích đáy và \( h \) là chiều cao.
- Thể tích hình chóp: \[ V = \frac{1}{3} \times S_{đáy} \times h \]
- Diện tích bề mặt hình cầu: \[ S = 4 \times \pi \times R^2 \] với \( R \) là bán kính của hình cầu.
- Thể tích hình cầu: \[ V = \frac{4}{3} \times \pi \times R^3 \]
2. Ví Dụ Minh Họa
Cho một hình chóp có diện tích đáy là \( S_{đáy} = 20 \, cm^2 \) và chiều cao \( h = 10 \, cm \). Hãy tính thể tích của hình chóp này.
Giải:
Áp dụng công thức thể tích hình chóp:
\[ V = \frac{1}{3} \times S_{đáy} \times h = \frac{1}{3} \times 20 \times 10 = \frac{200}{3} \, cm^3 \]
3. Bài Tập Tự Luyện
- Tính thể tích và diện tích bề mặt của một hình cầu có bán kính \( R = 5 \, cm \).
- Một hình lăng trụ đứng có đáy là tam giác đều với cạnh đáy \( a = 6 \, cm \) và chiều cao \( h = 12 \, cm \). Tính thể tích của hình lăng trụ.
- Tính thể tích của một hình nón có bán kính đáy \( r = 3 \, cm \) và chiều cao \( h = 9 \, cm \).
4. Lời Kết
Hình học không gian không chỉ giúp bạn hiểu rõ hơn về thế giới xung quanh mà còn phát triển khả năng tư duy logic và hình dung không gian. Hãy tiếp tục rèn luyện và áp dụng kiến thức này vào các bài toán thực tế.
Bài Tập 7: Xác Suất Và Thống Kê
Trong bài tập này, chúng ta sẽ áp dụng lý thuyết xác suất và thống kê để giải quyết các bài toán thực tế. Bạn sẽ học cách sử dụng các công cụ thống kê để phân tích dữ liệu và dự đoán kết quả. Dưới đây là các bước chi tiết để hoàn thành bài tập:
Bước 1: Tìm hiểu khái niệm cơ bản về xác suất
- Xác suất là một con số thể hiện khả năng xảy ra của một sự kiện. Giá trị của xác suất luôn nằm trong khoảng từ 0 đến 1.
- Công thức xác suất cơ bản: \[P(A) = \frac{\text{số kết quả thuận lợi}}{\text{tổng số kết quả có thể xảy ra}}\]
Bước 2: Thống kê mô tả
Thống kê mô tả giúp tóm tắt và mô tả các đặc điểm chính của tập dữ liệu. Các tham số thường được sử dụng bao gồm:
- Giá trị trung bình (Mean): \[\bar{x} = \frac{\sum_{i=1}^n x_i}{n}\]
- Trung vị (Median): Là giá trị nằm giữa tập dữ liệu đã được sắp xếp.
- Phương sai (Variance): \[\sigma^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n}\]
- Độ lệch chuẩn (Standard Deviation): \[\sigma = \sqrt{\sigma^2}\]
Bước 3: Xác suất có điều kiện
Xác suất có điều kiện là xác suất của một sự kiện xảy ra khi biết một sự kiện khác đã xảy ra. Công thức xác suất có điều kiện:
- \[P(A|B) = \frac{P(A \cap B)}{P(B)}\] nếu \(P(B) \neq 0\).
Bước 4: Sử dụng phân phối xác suất
Một số phân phối xác suất thường gặp trong xác suất và thống kê bao gồm:
- Phân phối nhị thức: \[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\], trong đó \(X\) là số lần thành công, \(n\) là số lần thử, và \(p\) là xác suất thành công trong mỗi lần thử.
- Phân phối chuẩn: \[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\], với \( \mu \) là giá trị trung bình và \( \sigma \) là độ lệch chuẩn.
Bước 5: Phân tích kết quả và dự đoán
Sau khi đã tính toán các tham số thống kê và xác suất, bạn có thể sử dụng chúng để phân tích dữ liệu và đưa ra dự đoán. Điều này có thể áp dụng vào các tình huống thực tế như dự đoán kết quả trận đấu bóng đá dựa trên dữ liệu thống kê trước đó.
Bước 6: Bài tập thực hành
- Tính xác suất một đội bóng sẽ thắng trong một trận đấu dựa trên dữ liệu lịch sử.
- Tính phương sai và độ lệch chuẩn của số bàn thắng ghi được bởi một đội bóng trong một mùa giải.
- Phân tích phân phối nhị thức để dự đoán số trận thắng của một đội trong 10 trận đấu tới.
Hãy cố gắng hoàn thành tất cả các bước trên và sử dụng các công thức một cách chính xác. Chúc bạn thành công!
Bài Tập 8: Phương Trình Vi Phân
Phương trình vi phân là một công cụ quan trọng trong toán học, được sử dụng để mô tả các hiện tượng biến thiên trong tự nhiên và xã hội. Dưới đây là một số bài tập về phương trình vi phân kèm lời giải chi tiết, giúp bạn nắm vững các khái niệm cơ bản.
-
Bài tập 1: Giải phương trình vi phân bậc nhất
Xét phương trình vi phân:
\[ \frac{dy}{dx} = y + x \]Lời giải: Để giải phương trình này, chúng ta áp dụng phương pháp tích phân. Đầu tiên, tách biến:
\[ \frac{dy}{y + x} = dx \]Tiếp theo, tích phân hai vế:
\[ \int \frac{dy}{y + x} = \int dx \]Kết quả của quá trình tích phân là:
\[ \ln|y + x| = x + C \]Vậy nghiệm của phương trình vi phân là:
\[ y + x = e^{x + C} \]Hoặc có thể viết lại dưới dạng:
\[ y = e^{x + C} - x \] -
Bài tập 2: Phương trình vi phân bậc hai
Xét phương trình vi phân:
\[ y'' - 3y' + 2y = 0 \]Lời giải: Đây là phương trình vi phân tuyến tính bậc hai có nghiệm đặc trưng. Trước tiên, chúng ta tìm nghiệm của phương trình đặc trưng:
\[ r^2 - 3r + 2 = 0 \]Giải phương trình bậc hai này, ta được hai nghiệm:
\[ r_1 = 1, \quad r_2 = 2 \]Vậy nghiệm tổng quát của phương trình là:
\[ y(t) = C_1 e^{r_1 t} + C_2 e^{r_2 t} = C_1 e^t + C_2 e^{2t} \]
Thông qua các bài tập này, bạn sẽ hiểu rõ hơn về cách giải phương trình vi phân và ứng dụng của chúng trong việc mô tả các hiện tượng tự nhiên.
Bài Tập 9: Hình Học Giải Tích
Trong bài tập này, chúng ta sẽ khám phá một số khái niệm cơ bản về Hình Học Giải Tích, bao gồm cách xác định phương trình đường thẳng, mặt phẳng trong không gian, và tính toán khoảng cách giữa các đối tượng hình học. Hãy bắt đầu với các bước sau:
Bước 1: Phương trình đường thẳng trong không gian
Một đường thẳng trong không gian có thể được xác định bằng cách sử dụng một điểm \( A(x_1, y_1, z_1) \) và một vector chỉ phương \( \vec{u} = (a, b, c) \). Phương trình tham số của đường thẳng là:
Với \( t \) là tham số thực.
Bước 2: Phương trình mặt phẳng
Một mặt phẳng có thể được biểu diễn dưới dạng tổng quát như sau:
Trong đó, \( A, B, C \) là các hệ số xác định vector pháp tuyến của mặt phẳng, và \( D \) là hằng số.
Bước 3: Tính khoảng cách từ một điểm đến một đường thẳng
Giả sử cần tính khoảng cách từ điểm \( M(x_0, y_0, z_0) \) đến đường thẳng xác định bởi điểm \( A(x_1, y_1, z_1) \) và vector chỉ phương \( \vec{u} = (a, b, c) \). Công thức tính khoảng cách là:
Bước 4: Bài tập thực hành
- Cho điểm \( P(1, 2, 3) \) và đường thẳng \( d \) có phương trình tham số \( \begin{cases} x = 1 + 2t \\ y = 2 - t \\ z = 3 + 4t \end{cases} \). Hãy tính khoảng cách từ điểm \( P \) đến đường thẳng \( d \).
- Cho mặt phẳng \( \Pi: 2x - 3y + z + 5 = 0 \) và điểm \( Q(4, 1, -2) \). Hãy xác định tọa độ điểm đối xứng của \( Q \) qua mặt phẳng \( \Pi \).
Hãy giải các bài tập trên và đối chiếu với đáp án của mình để kiểm tra kết quả. Chúc các bạn học tốt!
Bài Tập 10: Bất Đẳng Thức Và Bất Phương Trình
Bài tập này sẽ giúp bạn nắm vững các khái niệm cơ bản về bất đẳng thức và bất phương trình. Chúng ta sẽ cùng đi qua các ví dụ cụ thể và phương pháp giải chi tiết.
- Bài 1: Bất đẳng thức cơ bản
- Bài 2: Bất phương trình bậc nhất
- Trừ 3 cả hai vế: \(2x + 3 - 3 \leq 7 - 3\) dẫn đến \(2x \leq 4\).
- Chia cả hai vế cho 2: \[ x \leq 2 \]
- Bài 3: Bất phương trình bậc hai
- Phân tích phương trình thành các nhân tử: \((x - 1)(x - 3) > 0\).
- Phân tích nghiệm: Bất phương trình sẽ có nghiệm khi \(x < 1\) hoặc \(x > 3\).
Cho bất đẳng thức \(a + b > c\). Hãy chứng minh bất đẳng thức này và tìm nghiệm của nó trong trường hợp cụ thể với các giá trị \(a = 2\), \(b = 3\), và \(c = 4\).
Hướng dẫn: Áp dụng các quy tắc cơ bản của bất đẳng thức và thay thế các giá trị cụ thể vào, ta có:
\[
2 + 3 > 4
\]
Điều này đúng vì \(5 > 4\).
Giải bất phương trình sau: \(2x + 3 \leq 7\).
Giải:
Vậy nghiệm của bất phương trình là \(x \leq 2\).
Giải bất phương trình \(x^2 - 4x + 3 > 0\).
Giải: