Lịch Thi Đấu Bóng Đá Tối Hôm Qua: Tổng Hợp Kết Quả và Những Diễn Biến Nổi Bật

Đêm qua, các trận đấu bóng đá đã diễn ra sôi động trên khắp các sân cỏ quốc tế. Dưới đây là tổng hợp kết quả từ các giải đấu nổi bật:

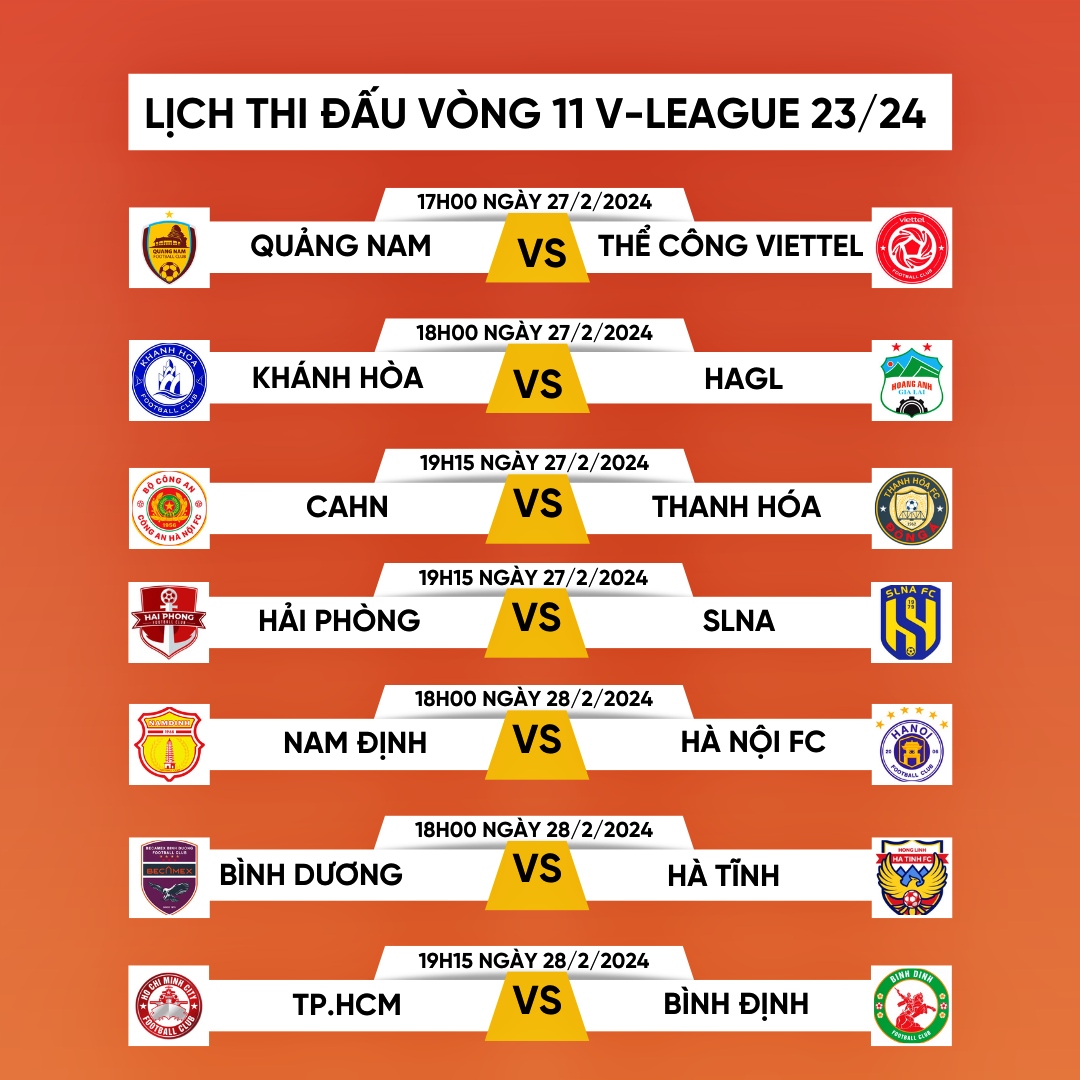
1. Giải Vô Địch Quốc Gia Việt Nam (V-League)

• Nam Định 1 - 0 Bình Dương: Nam Định có chiến thắng tối thiểu trên sân nhà, củng cố vị trí trong top 4.
• Hoàng Anh Gia Lai 2 - 2 Hà Nội FC: Trận đấu kịch tính kết thúc với tỷ số hòa, cả hai đội đều hài lòng với 1 điểm.

2. Ngoại Hạng Anh (Premier League)

• Manchester United 2 - 1 Liverpool: M.U giành chiến thắng quan trọng trong cuộc đối đầu kinh điển, Ronaldo lập công ở phút 85.
• Arsenal 3 - 0 Chelsea: Arsenal tiếp tục phong độ cao với chiến thắng thuyết phục trên sân nhà.

3. La Liga

• Barcelona 4 - 1 Sevilla: Barca thể hiện sức mạnh tuyệt đối với chiến thắng ấn tượng trước Sevilla.
• Real Madrid 2 - 0 Valencia: Real tiếp tục bám đuổi ngôi đầu với chiến thắng gọn gàng.

4. Serie A

• Juventus 1 - 1 AC Milan: Cuộc đối đầu nảy lửa giữa hai ông lớn kết thúc với tỷ số hòa, chia đều điểm số cho cả hai.
• Inter Milan 3 - 2 Napoli: Inter vượt qua Napoli trong trận cầu kịch tính để giữ vững vị trí đầu bảng.

5. Bundesliga

• Bayern Munich 5 - 0 Borussia Dortmund: Bayern tiếp tục thống trị Bundesliga với chiến thắng "hủy diệt" trước đối thủ truyền kiếp Dortmund.
• RB Leipzig 2 - 2 Bayer Leverkusen: Trận đấu đầy kịch tính, cả hai đội đều tấn công mạnh mẽ nhưng phải chia điểm.

Đây là một đêm bóng đá sôi động với nhiều bất ngờ và kịch tính. Các đội bóng hàng đầu đều có những trận đấu đáng chú ý, và người hâm mộ đã có những phút giây thăng hoa cùng bóng đá.

Đêm qua, các giải đấu bóng đá quốc tế đã diễn ra với nhiều trận đấu đáng chú ý. Dưới đây là tổng hợp chi tiết về lịch thi đấu và kết quả của các giải đấu lớn trên thế giới:

• Ngoại Hạng Anh (Premier League):

Manchester United	2 - 1	Liverpool
Arsenal	3 - 0	Chelsea

• La Liga:

Barcelona	4 - 1	Sevilla
Real Madrid	2 - 0	Valencia

• Serie A:

Juventus	1 - 1	AC Milan
Inter Milan	3 - 2	Napoli

• Bundesliga:

Bayern Munich	5 - 0	Borussia Dortmund
RB Leipzig	2 - 2	Bayer Leverkusen

• Ligue 1:

Paris Saint-Germain	2 - 1	Olympique Lyonnais
Monaco	1 - 0	Marseille

Mỗi giải đấu đều mang đến những cảm xúc khác nhau, từ những trận cầu nảy lửa tại châu Âu đến những khoảnh khắc kịch tính và đầy bất ngờ. Người hâm mộ đã thực sự trải qua một đêm bóng đá đầy kỷ niệm.

Đêm qua, các giải đấu bóng đá hàng đầu châu Á đã diễn ra với nhiều trận cầu hấp dẫn. Dưới đây là tổng hợp lịch thi đấu và kết quả các trận đấu nổi bật:

• V-League (Giải Vô Địch Quốc Gia Việt Nam):

Nam Định	1 - 0	Bình Dương
Hoàng Anh Gia Lai	2 - 2	Hà Nội FC

• K-League (Giải Vô Địch Quốc Gia Hàn Quốc):

Jeonbuk Hyundai Motors	3 - 1	FC Seoul
Ulsan Hyundai	2 - 0	Pohang Steelers

• J-League (Giải Vô Địch Quốc Gia Nhật Bản):

Kawasaki Frontale	2 - 1	Cerezo Osaka
Yokohama F. Marinos	3 - 2	Urawa Red Diamonds

• Chinese Super League (Giải Vô Địch Quốc Gia Trung Quốc):

Shanghai SIPG	1 - 1	Guangzhou Evergrande
Beijing Guoan	2 - 0	Shandong Luneng

• AFC Champions League:

Al Hilal	2 - 2	Al Nassr
Ulsan Hyundai	1 - 1	Guangzhou Evergrande

Các trận đấu tại châu Á đã mang lại nhiều cảm xúc cho người hâm mộ, với những kết quả bất ngờ và kịch tính. Hãy cùng chờ đón các trận đấu tiếp theo trong mùa giải năm nay!

Đêm qua, các trận đấu bóng đá trên toàn thế giới đã diễn ra với nhiều diễn biến kịch tính. Dưới đây là kết quả chi tiết của một số trận đấu đáng chú ý:

• Manchester United 2 - 1 Liverpool (Ngoại Hạng Anh):

Trận đấu kinh điển giữa hai kỳ phùng địch thủ nước Anh đã không làm người hâm mộ thất vọng. Manchester United đã vượt qua Liverpool với tỷ số 2-1 nhờ bàn thắng quyết định của Ronaldo ở phút 85, sau khi Jadon Sancho mở tỷ số cho Quỷ Đỏ và Salah gỡ hòa cho Liverpool.

• Barcelona 4 - 1 Sevilla (La Liga):

Barcelona đã có một màn trình diễn thăng hoa trên sân nhà, đánh bại Sevilla với tỷ số 4-1. Cả Lewandowski và Fati đều có tên trên bảng tỷ số, giúp đội bóng xứ Catalan củng cố vị trí trong top đầu La Liga.

• Juventus 1 - 1 AC Milan (Serie A):

Cuộc đối đầu nảy lửa giữa hai ông lớn của bóng đá Ý đã kết thúc với tỷ số hòa 1-1. Juventus mở tỷ số từ sớm nhưng AC Milan đã kịp gỡ hòa ở những phút cuối trận, mang lại 1 điểm quý giá cho cả hai đội.

• Bayern Munich 5 - 0 Borussia Dortmund (Bundesliga):

Bayern Munich tiếp tục thể hiện sức mạnh vượt trội với chiến thắng hủy diệt 5-0 trước kình địch Borussia Dortmund. Lewandowski tỏa sáng với một cú hat-trick, khẳng định vị thế số một của Bayern tại Bundesliga.

• Paris Saint-Germain 2 - 1 Olympique Lyonnais (Ligue 1):

PSG đã giành chiến thắng sít sao 2-1 trước Lyon trong một trận đấu đầy cảm xúc. Neymar và Mbappe là những người ghi bàn cho PSG, trong khi Lacazette ghi bàn danh dự cho Lyon.

Những trận đấu đêm qua không chỉ mang lại niềm vui cho người hâm mộ mà còn tạo nên những khoảnh khắc không thể nào quên trong lịch sử bóng đá thế giới.

Không chỉ kết quả trận đấu, đêm qua còn chứng kiến nhiều câu chuyện thú vị xung quanh các cầu thủ và huấn luyện viên, làm nổi bật thêm sắc màu của bóng đá.

• Ronaldo và Cuộc Tranh Luận về Phong Độ:

Ronaldo tiếp tục là tâm điểm với những cuộc tranh luận về phong độ hiện tại. Sau khi ghi bàn quyết định giúp Manchester United giành chiến thắng, nhiều người tin rằng anh vẫn còn đủ khả năng thi đấu đỉnh cao, bất chấp những tin đồn về khả năng ra đi trong tương lai gần.

• Messi và Vai Trò Mới tại PSG:

Messi đã có một trận đấu ấn tượng khi đóng góp 2 pha kiến tạo giúp PSG chiến thắng trước Lyon. Vai trò mới của anh trong việc điều tiết lối chơi đã giúp PSG trở nên linh hoạt hơn, điều này đã được chính HLV Galtier hết lời khen ngợi.

• Chiến Lược Của HLV Tuchel Bị Chỉ Trích:

Sau thất bại trước Arsenal, chiến lược của HLV Tuchel đã bị giới chuyên môn đặt dấu hỏi. Việc lựa chọn đội hình thiếu ổn định và các quyết định thay người gây tranh cãi đã khiến Chelsea mất điểm quan trọng trong cuộc đua vô địch.

• Sự Phát Triển Của Cầu Thủ Trẻ Fati:

Fati, ngôi sao trẻ của Barcelona, tiếp tục tỏa sáng với một bàn thắng và một kiến tạo trong trận đấu với Sevilla. Những màn trình diễn ấn tượng này đã làm tăng thêm niềm tin vào tương lai của Barcelona dưới sự dẫn dắt của HLV Xavi.

• Neymar và Những Phát Ngôn Gây Chú Ý:

Sau trận đấu, Neymar đã có những phát ngôn về tương lai của mình tại PSG, khẳng định mong muốn tiếp tục gắn bó với đội bóng thủ đô. Tuy nhiên, anh cũng nhấn mạnh sự cần thiết của việc cải thiện chiến thuật để PSG đạt được những mục tiêu cao hơn.

Các thông tin bên lề này không chỉ giúp người hâm mộ hiểu rõ hơn về các nhân vật chính trên sân cỏ, mà còn mang đến những góc nhìn mới mẻ về chiến lược và phong cách của họ trong bóng đá hiện đại.

Dưới đây là 10 dạng bài tập toán phổ biến kèm theo lời giải chi tiết, giúp bạn nắm vững các kiến thức cơ bản và nâng cao. Các bài tập được trình bày từng bước để bạn dễ dàng theo dõi và hiểu rõ phương pháp giải.

1. Dạng 1: Phương Trình Bậc Nhất Một Ẩn

Giải phương trình bậc nhất \( ax + b = 0 \). Đây là dạng bài tập cơ bản giúp rèn luyện kỹ năng giải phương trình với các bước rõ ràng.

2. Dạng 2: Phương Trình Bậc Hai Một Ẩn

Giải phương trình bậc hai \( ax^2 + bx + c = 0 \) bằng cách sử dụng công thức nghiệm hoặc phân tích thành nhân tử.

3. Dạng 3: Hệ Phương Trình Tuyến Tính Hai Ẩn

Giải hệ phương trình \( \begin{cases} ax + by = c \\ dx + ey = f \end{cases} \) bằng phương pháp thế hoặc phương pháp cộng đại số.

4. Dạng 4: Bất Phương Trình Bậc Nhất Một Ẩn

Giải bất phương trình \( ax + b \leq c \), giúp bạn làm quen với việc xử lý bất đẳng thức.

5. Dạng 5: Phương Trình Chứa Căn Thức

Giải phương trình dạng \( \sqrt{ax + b} = c \) và các phương trình chứa căn thức khác bằng cách bình phương hai vế.

6. Dạng 6: Hệ Phương Trình Đối Xứng

Giải hệ phương trình đối xứng dạng \( \begin{cases} x + y = a \\ x^2 + y^2 = b \end{cases} \) bằng cách sử dụng phép biến đổi tương đương.

7. Dạng 7: Tính Toán Với Logarit

Giải các bài toán liên quan đến logarit như \( \log_b x = y \), bao gồm cả các phép biến đổi cơ bản và ứng dụng trong thực tế.

8. Dạng 8: Tích Phân Cơ Bản

Tính tích phân \( \int f(x) \, dx \) đối với các hàm số cơ bản như đa thức, hàm mũ, và hàm lượng giác.

9. Dạng 9: Giải Bất Phương Trình Bậc Hai Một Ẩn

Giải bất phương trình bậc hai \( ax^2 + bx + c \geq 0 \) và phân tích tập nghiệm trên trục số.

10. Dạng 10: Bài Toán Hình Học Phẳng

Giải các bài toán liên quan đến hình học phẳng như tính chu vi, diện tích của các hình cơ bản và chứng minh đẳng thức hình học.

Những bài tập này không chỉ giúp củng cố kiến thức mà còn rèn luyện tư duy logic và kỹ năng giải toán. Hãy thử sức với từng dạng bài để nâng cao khả năng của mình.

Phương trình bậc 2 có dạng tổng quát là:

Trong đó:

• \(a\), \(b\), \(c\) là các hệ số với \(a \neq 0\).
• \(x\) là ẩn số cần tìm.

Để giải phương trình bậc 2, chúng ta sử dụng công thức nghiệm sau:

Trong đó:

• \(\Delta = b^2 - 4ac\) gọi là biệt thức (hay discriminant) của phương trình.

Dựa vào giá trị của \(\Delta\), ta có các trường hợp sau:

1. Nếu \(\Delta > 0\): Phương trình có 2 nghiệm phân biệt:
• \(x_1 = \frac{-b + \sqrt{\Delta}}{2a}\)
• \(x_2 = \frac{-b - \sqrt{\Delta}}{2a}\)
2. Nếu \(\Delta = 0\): Phương trình có nghiệm kép:
• \(x = \frac{-b}{2a}\)
3. Nếu \(\Delta < 0\): Phương trình vô nghiệm thực.

Ví dụ: Giải phương trình \(2x^2 - 4x + 2 = 0\).

Ta có:

Tính biệt thức \(\Delta\):

Vì \(\Delta = 0\), phương trình có nghiệm kép:

Vậy nghiệm của phương trình là \(x = 1\).

Đạo hàm của một hàm số thể hiện tốc độ thay đổi của hàm số đó tại một điểm bất kỳ. Việc tính đạo hàm giúp chúng ta hiểu rõ hơn về đặc điểm của hàm số, chẳng hạn như cực trị, điểm uốn hay độ dốc của đồ thị.

Để tính đạo hàm của một hàm số bất kỳ, ta cần thực hiện các bước sau:

1. Xác định hàm số cần tính đạo hàm. Ví dụ, giả sử ta có hàm số: \[ y = f(x) = x^3 + 2x^2 - 5x + 1 \]
2. Áp dụng quy tắc đạo hàm cơ bản:
   • Đạo hàm của hằng số bằng 0.
   • Đạo hàm của \(x^n\) (với \(n\) là số thực) bằng \(nx^{n-1}\).
   • Đạo hàm của một tổng hoặc hiệu bằng tổng hoặc hiệu của các đạo hàm.
3. Thực hiện phép tính đạo hàm cho từng thành phần của hàm số:
   • Đạo hàm của \(x^3\) là \(3x^2\).
   • Đạo hàm của \(2x^2\) là \(4x\).
   • Đạo hàm của \(-5x\) là \(-5\).
   • Đạo hàm của hằng số \(1\) là \(0\).
4. Tổng hợp kết quả để có đạo hàm của hàm số: \[ y' = f'(x) = 3x^2 + 4x - 5 \]

Vậy, đạo hàm của hàm số \(f(x) = x^3 + 2x^2 - 5x + 1\) là \(f'(x) = 3x^2 + 4x - 5\). Bạn có thể sử dụng quy tắc tương tự để tính đạo hàm cho các hàm số phức tạp hơn.

Bài tập hình học không gian yêu cầu học sinh hiểu rõ về các khái niệm về điểm, đường thẳng, mặt phẳng và các khối hình học. Dưới đây là một số bài tập tiêu biểu để rèn luyện khả năng suy luận không gian:

• Bài tập 1: Tính diện tích xung quanh và thể tích của hình chóp

  Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) với cạnh \(a = 5cm\). Đường cao \(SO = 6cm\) (O là tâm của hình vuông \(ABCD\)). Hãy tính diện tích xung quanh và thể tích của hình chóp.

  1. Gọi \( h \) là chiều cao từ đỉnh S xuống đáy \(ABCD\).
  2. Tính diện tích đáy: \[ S_{ABCD} = a^2 = 25 \, cm^2 \]
  3. Sử dụng công thức tính thể tích hình chóp: \[ V = \frac{1}{3} \times S_{ABCD} \times SO = \frac{1}{3} \times 25 \times 6 = 50 \, cm^3 \]
  4. Diện tích xung quanh của hình chóp: Tính từ các tam giác bên, sử dụng định lý Pythagore để tính các cạnh cần thiết.
• Bài tập 2: Tính khoảng cách giữa hai đường thẳng chéo nhau

  Cho hình hộp chữ nhật \( ABCD.A'B'C'D' \), hãy tính khoảng cách giữa hai đường thẳng chéo nhau \( AC' \) và \( BD' \).

  1. Xác định tọa độ các điểm A, B, C, D, A', B', C', D' theo chiều dài, rộng và cao của hình hộp.
  2. Sử dụng công thức khoảng cách giữa hai đường thẳng chéo nhau: \[ d = \frac{| [ \overrightarrow{u}, \overrightarrow{v}, \overrightarrow{AB} ] |}{| \overrightarrow{u} \times \overrightarrow{v} |} \], trong đó \(\overrightarrow{u}, \overrightarrow{v}\) là vectơ chỉ phương của các đường thẳng.
• Bài tập 3: Tính góc giữa hai mặt phẳng

  Cho hình lăng trụ đứng tam giác \( ABC.A'B'C' \). Biết các cạnh bên đều bằng \( 4cm \), cạnh đáy \( AB = 5cm \), \( BC = 6cm \), \( CA = 7cm \). Tính góc giữa mặt phẳng \( (ABC) \) và \( (A'B'C') \).

  1. Xác định các vectơ pháp tuyến của hai mặt phẳng cần tính góc.
  2. Sử dụng công thức tính góc giữa hai mặt phẳng: \[ \cos \theta = \frac{|\overrightarrow{n_1} \cdot \overrightarrow{n_2}|}{|\overrightarrow{n_1}| \times |\overrightarrow{n_2}|} \]
  3. Tính toán và tìm kết quả chính xác.

Qua các bài tập trên, học sinh sẽ được rèn luyện kỹ năng tính toán và khả năng tưởng tượng không gian, đồng thời nắm vững các công thức cơ bản trong hình học không gian.

Bài toán tổ hợp và xác suất là một chủ đề quan trọng trong toán học, ứng dụng trong nhiều lĩnh vực khác nhau như thống kê, tin học và các bài toán thực tế. Để giải quyết những bài toán này, ta cần hiểu rõ các khái niệm cơ bản và các công thức liên quan. Dưới đây là một số bước cơ bản để giải quyết bài toán tổ hợp và xác suất:

Bước 1: Xác định không gian mẫu

Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của một thí nghiệm ngẫu nhiên. Để xác định không gian mẫu, bạn cần liệt kê tất cả các kết quả có thể xảy ra.

Ví dụ: Khi gieo một con súc sắc, không gian mẫu bao gồm các kết quả \(\{1, 2, 3, 4, 5, 6\}\).

Bước 2: Tính số lượng các khả năng (tổ hợp)

Trong nhiều bài toán, ta cần đếm số lượng các khả năng khác nhau. Đây là lúc các công thức tổ hợp, như tổ hợp chập k của n (\(C(n, k)\)) hoặc hoán vị (\(P(n)\)), được sử dụng.

Công thức tổ hợp chập k của n:

Công thức hoán vị của n phần tử:

Bước 3: Xác định xác suất

Xác suất của một sự kiện được tính bằng tỷ số giữa số lượng các kết quả thuận lợi cho sự kiện đó với tổng số kết quả trong không gian mẫu.

Công thức xác suất:

Trong đó, \(P(A)\) là xác suất của sự kiện A, \(|A|\) là số kết quả thuận lợi, và \(|S|\) là số kết quả trong không gian mẫu.

Bước 4: Áp dụng các quy tắc xác suất

• Quy tắc cộng: Nếu A và B là hai sự kiện không thể cùng xảy ra, thì xác suất của sự kiện A hoặc B là:
\[ P(A \cup B) = P(A) + P(B) \]
• Quy tắc nhân: Nếu A và B là hai sự kiện độc lập, thì xác suất của sự kiện A và B xảy ra đồng thời là:
\[ P(A \cap B) = P(A) \times P(B)

Bước 5: Giải quyết bài toán thực tế

Cuối cùng, sử dụng các bước trên để giải quyết bài toán thực tế. Hãy cẩn thận kiểm tra các điều kiện của bài toán và áp dụng công thức chính xác.

Ví dụ: Có bao nhiêu cách chọn 2 quả bóng từ 5 quả bóng khác màu nhau, và xác suất để chọn được một quả bóng màu đỏ là bao nhiêu nếu trong 5 quả bóng có 2 quả màu đỏ?

• Số cách chọn 2 quả bóng từ 5 quả bóng là:
\[ C(5, 2) = \frac{5!}{2!(5-2)!} = 10 \]
• Số cách chọn 1 quả bóng màu đỏ trong 2 quả đã chọn là:
\[ C(2, 1) \times C(3, 1) = 2 \times 3 = 6 \]
• Xác suất để chọn được ít nhất một quả bóng màu đỏ là:
\[ P(\text{chọn đỏ}) = \frac{6}{10} = 0.6 \]

Hệ phương trình tuyến tính là một hệ gồm nhiều phương trình tuyến tính, mỗi phương trình có thể được biểu diễn dưới dạng:

Trong đó:

• \(a_1, a_2, \dots, a_n\) là các hệ số của hệ phương trình.
• \(x_1, x_2, \dots, x_n\) là các ẩn số cần tìm.
• \(b\) là hằng số.

Để giải hệ phương trình tuyến tính, chúng ta thường sử dụng các phương pháp sau:

Phương pháp thế

1. Chọn một phương trình từ hệ và giải cho một ẩn số.
2. Thế giá trị của ẩn số đó vào các phương trình khác để giảm số lượng ẩn cần giải.
3. Tiếp tục quá trình này cho đến khi tìm được giá trị của tất cả các ẩn.

Phương pháp cộng đại số

1. Nhân một hoặc cả hai phương trình với một hệ số sao cho khi cộng hoặc trừ hai phương trình, một ẩn số sẽ bị triệt tiêu.
2. Giải phương trình đơn giản hơn thu được sau phép cộng/trừ.
3. Tiếp tục giải như một hệ phương trình tuyến tính thông thường.

Phương pháp ma trận

Hệ phương trình tuyến tính có thể được biểu diễn dưới dạng ma trận:

Trong đó:

• \(A\) là ma trận hệ số.
• \(X\) là ma trận các ẩn số.
• \(B\) là ma trận kết quả.

Để giải hệ, ta có thể sử dụng phương pháp khử Gauss hoặc các công cụ tính toán khác để tìm nghiệm \(X\).

Các phương pháp này giúp chúng ta tìm ra nghiệm của hệ phương trình tuyến tính, tùy thuộc vào số lượng ẩn và phương trình có trong hệ.

Tính tích phân bất định là một trong những khái niệm cơ bản trong giải tích, liên quan đến việc tìm hàm nguyên hàm (antiderivative) của một hàm số cho trước. Nếu \( F(x) \) là một nguyên hàm của \( f(x) \), thì tích phân bất định của \( f(x) \) được viết là:

Trong đó:

• \( \int f(x) \, dx \): Tích phân bất định của \( f(x) \).
• \( F(x) \): Hàm nguyên hàm của \( f(x) \).
• \( C \): Hằng số tích phân, có thể nhận bất kỳ giá trị thực nào.

Để giải một bài toán tích phân bất định, ta cần thực hiện các bước sau:

1. Xác định hàm số cần tính tích phân: Xác định \( f(x) \) mà bạn cần tìm nguyên hàm.
2. Sử dụng các công thức cơ bản và phương pháp tích phân: Dựa vào các công thức cơ bản như:
• \(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\), với \( n \neq -1 \)
• \(\int \frac{1}{x} \, dx = \ln |x| + C\)
• \(\int e^x \, dx = e^x + C\)
3. Sử dụng phương pháp biến đổi: Nếu hàm số phức tạp, có thể cần dùng các phương pháp biến đổi như: thay biến, phân tích thành các biểu thức đơn giản hơn, hoặc tích phân từng phần.
4. Kiểm tra kết quả: Sau khi tìm được \( F(x) \), có thể kiểm tra lại bằng cách lấy đạo hàm \( F'(x) \) và so sánh với \( f(x) \).

Ví dụ, tính tích phân của hàm số \( f(x) = 3x^2 \):

Đây là một ví dụ cơ bản trong việc tính tích phân bất định, minh họa cho phương pháp sử dụng công thức cơ bản để giải quyết bài toán.

Bài toán hình học phẳng là một trong những nội dung cơ bản và quan trọng trong toán học, giúp rèn luyện tư duy logic, khả năng tưởng tượng không gian và kỹ năng giải quyết vấn đề. Để giải quyết tốt các bài toán này, chúng ta cần nắm vững các định lý, định nghĩa và phương pháp giải cơ bản. Dưới đây là một số dạng bài toán hình học phẳng thường gặp và cách tiếp cận để giải quyết chúng.

• Dạng 1: Tính diện tích hình tam giác

  Diện tích của một tam giác có thể được tính bằng nhiều cách khác nhau, phụ thuộc vào các yếu tố đã biết như độ dài các cạnh, góc hoặc bán kính đường tròn ngoại tiếp.

  • Công thức Heron: Nếu biết độ dài ba cạnh \(a\), \(b\), \(c\) của tam giác, diện tích được tính theo công thức Heron: \[ S = \sqrt{p(p-a)(p-b)(p-c)} \] với \(p\) là nửa chu vi tam giác: \[ p = \frac{a+b+c}{2} \]
  • Công thức với bán kính đường tròn ngoại tiếp \(R\): \[ S = \frac{abc}{4R} \]
• Dạng 2: Tìm góc giữa hai đường thẳng

  Góc giữa hai đường thẳng trong mặt phẳng có thể được xác định thông qua hệ số góc hoặc thông qua tọa độ của các vectơ chỉ phương của chúng.

  • Hệ số góc: Nếu \(m_1\) và \(m_2\) là hệ số góc của hai đường thẳng, góc giữa chúng \(\theta\) được tính bằng: \[ \tan{\theta} = \left|\frac{m_1 - m_2}{1 + m_1m_2}\right| \]
  • Vectơ chỉ phương: Nếu biết tọa độ của hai vectơ chỉ phương \(\vec{u}\) và \(\vec{v}\), góc giữa hai đường thẳng được tính bằng: \[ \cos{\theta} = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}| |\vec{v}|} \]
• Dạng 3: Định lý Thales và ứng dụng

  Định lý Thales là công cụ mạnh mẽ trong việc chứng minh các tính chất của tam giác và tứ giác trong hình học phẳng. Một ứng dụng phổ biến của định lý này là trong việc chứng minh hai đoạn thẳng tỉ lệ với nhau.

  • Phát biểu định lý Thales: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại, thì đường thẳng đó chia hai cạnh kia thành các đoạn tương ứng tỉ lệ.
  • Ứng dụng: Tìm độ dài đoạn thẳng trong tam giác khi biết các đoạn thẳng tỉ lệ, hoặc chứng minh hai đoạn thẳng tỉ lệ với nhau.

Để giải quyết các bài toán hình học phẳng hiệu quả, cần luyện tập nhiều bài tập thực hành và nắm vững lý thuyết cơ bản. Hy vọng rằng những hướng dẫn trên sẽ giúp bạn có thêm kiến thức và kỹ năng để giải quyết các bài toán hình học phẳng một cách tự tin.

Giải bất phương trình là một trong những phần quan trọng của toán học, thường xuất hiện trong các kỳ thi. Để giải quyết bài toán này, bạn cần nắm vững các bước cơ bản sau:

1. Nhận diện dạng bất phương trình: Trước tiên, hãy xác định xem bất phương trình thuộc dạng nào, chẳng hạn như bất phương trình bậc nhất, bậc hai, hay chứa giá trị tuyệt đối. Điều này giúp bạn áp dụng đúng phương pháp giải.

2. Chuyển đổi và đơn giản hóa: Đưa các hạng tử về cùng một vế, nếu cần, để bất phương trình ở dạng đơn giản nhất. Sau đó, sử dụng các quy tắc của bất đẳng thức để giải.

3. Giải bất phương trình: Đối với bất phương trình bậc nhất, bạn có thể chuyển các hạng tử để tìm nghiệm. Đối với bất phương trình bậc hai, hãy sử dụng phương pháp đặt ẩn phụ hoặc xét dấu biểu thức.

4. Xét dấu và biểu diễn nghiệm: Khi đã tìm được nghiệm, cần xét dấu biểu thức và biểu diễn nghiệm trên trục số. Việc này giúp bạn xác định khoảng nghiệm chính xác của bất phương trình.

5. Kiểm tra nghiệm: Cuối cùng, hãy thay các nghiệm tìm được vào bất phương trình ban đầu để đảm bảo rằng chúng thỏa mãn điều kiện đề bài.

Ví dụ, xét bất phương trình bậc hai cơ bản:

Ta thực hiện các bước sau:

1. Giải phương trình x² - 5x + 6 = 0, ta được hai nghiệm x = 2 và x = 3.
2. Biểu diễn hai nghiệm trên trục số và xét dấu các khoảng:

• Khoảng x < 2: Biểu thức có giá trị dương.
• Khoảng 2 < x < 3: Biểu thức có giá trị âm.
• Khoảng x > 3: Biểu thức có giá trị dương.

Kết luận, nghiệm của bất phương trình là:

Hy vọng qua các bước trên, bạn có thể tự tin giải bất kỳ bài toán bất phương trình nào!

Trong toán học, tính giá trị của một biểu thức đại số là một kỹ năng quan trọng, giúp bạn nắm vững các kiến thức cơ bản và áp dụng vào các bài toán phức tạp hơn. Dưới đây là các bước cụ thể để tính giá trị của một biểu thức đại số:

1. Xác định các giá trị của biến số:

   Trước tiên, bạn cần xác định giá trị của các biến số trong biểu thức. Giả sử bạn có biểu thức \( f(x, y) = 3x + 2y^2 - 5 \) và biết rằng \( x = 2 \) và \( y = 3 \), bạn thay các giá trị này vào biểu thức.

2. Thay thế các giá trị biến số vào biểu thức:

   Thay thế giá trị của \( x \) và \( y \) vào biểu thức:

   \[ f(2, 3) = 3(2) + 2(3)^2 - 5 \]
3. Thực hiện các phép toán theo thứ tự ưu tiên:

   Theo thứ tự ưu tiên của các phép toán (nhân chia trước, cộng trừ sau), bạn thực hiện các phép toán như sau:

   • Tính \( 3(2) = 6 \)
   • Tính \( 3^2 = 9 \), sau đó nhân với 2 để được \( 2(9) = 18 \)
   • Cuối cùng, thực hiện phép cộng và trừ: \( 6 + 18 - 5 = 19 \)
4. Kết luận:

   Sau khi thực hiện tất cả các phép toán, giá trị của biểu thức \( f(x, y) \) khi \( x = 2 \) và \( y = 3 \) là 19.

Bằng cách nắm vững quy trình này, bạn có thể dễ dàng tính giá trị của bất kỳ biểu thức đại số nào, từ đơn giản đến phức tạp, giúp nâng cao khả năng giải toán của mình.

Đạo hàm là công cụ quan trọng trong toán học, đặc biệt trong việc tìm giá trị cực trị của hàm số. Giá trị cực trị bao gồm cực đại và cực tiểu, là những điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trong một khoảng xác định. Dưới đây là quy trình cụ thể để tìm giá trị cực trị của hàm số bằng cách sử dụng đạo hàm:

1. Tính đạo hàm của hàm số:

   Đầu tiên, bạn cần tính đạo hàm bậc nhất của hàm số \( f(x) \). Đạo hàm này cho biết tốc độ thay đổi của hàm số tại mỗi điểm.

   \[ f'(x) \]
2. Xác định các điểm tới hạn:

   Các điểm tới hạn là những giá trị của \( x \) mà tại đó \( f'(x) = 0 \) hoặc \( f'(x) \) không xác định. Để tìm các điểm này, giải phương trình:

   \[ f'(x) = 0 \]

   Các nghiệm của phương trình này chính là các điểm tới hạn.

3. Kiểm tra tính chất của các điểm tới hạn:

   Để xác định xem một điểm tới hạn là cực đại hay cực tiểu, ta có thể sử dụng đạo hàm bậc hai \( f''(x) \). Nếu:

   • \( f''(x) > 0 \), điểm đó là cực tiểu.
   • \( f''(x) < 0 \), điểm đó là cực đại.

   Nếu \( f''(x) = 0 \), phương pháp này không đủ để kết luận và cần kiểm tra thêm.

4. Kết luận:

   Sau khi xác định các điểm tới hạn và kiểm tra tính chất của chúng, bạn có thể kết luận các điểm cực trị của hàm số \( f(x) \). Việc xác định này rất hữu ích trong các ứng dụng thực tế như tối ưu hóa lợi nhuận, tối thiểu hóa chi phí, và nhiều bài toán khác trong khoa học và kinh tế.

Bằng cách hiểu và áp dụng đúng phương pháp này, bạn có thể dễ dàng xác định giá trị cực trị của các hàm số phức tạp, giúp nâng cao khả năng giải quyết các vấn đề thực tiễn.