Chủ đề lịch thi đấu bóng đá wc: Lịch thi đấu bóng đá WC mang đến những thông tin chính xác và cập nhật nhất về giải đấu lớn nhất hành tinh. Bài viết này sẽ giúp bạn dễ dàng theo dõi lịch trình các trận đấu, khung giờ thi đấu và thông tin về các đội bóng tham gia World Cup, giúp bạn không bỏ lỡ bất kỳ trận cầu hấp dẫn nào.
Mục lục
- Lịch thi đấu bóng đá World Cup 2026 khu vực Châu Á
- Lịch thi đấu FIFA World Cup 2026 khu vực châu Á
- Lịch thi đấu cụ thể theo giờ Việt Nam
- Kết quả vòng loại World Cup 2026 khu vực châu Á
- Lịch thi đấu VCK World Cup 2022
- 10 bài tập Toán có lời giải hoàn chỉnh
- Dạng bài tập 1: Giải phương trình bậc hai
- Dạng bài tập 2: Tính diện tích hình tròn
- Dạng bài tập 3: Hệ phương trình tuyến tính
- Dạng bài tập 4: Đạo hàm và ứng dụng
- Dạng bài tập 5: Tính tích phân cơ bản
- Dạng bài tập 6: Bài tập về vectơ
- Dạng bài tập 7: Phương trình đường thẳng trong mặt phẳng
- Dạng bài tập 8: Xác suất và thống kê
- Dạng bài tập 9: Giải hệ bất phương trình
- Dạng bài tập 10: Tính thể tích khối chóp
Lịch thi đấu bóng đá World Cup 2026 khu vực Châu Á
Dưới đây là lịch thi đấu vòng loại World Cup 2026 khu vực Châu Á, trong đó có sự góp mặt của đội tuyển Việt Nam. Các trận đấu hứa hẹn mang đến những màn trình diễn hấp dẫn.
Lịch thi đấu đội tuyển Việt Nam tại vòng loại
| Ngày | Giờ | Đối thủ | Địa điểm |
|---|---|---|---|
| 12/06/2024 | 01:00 | Iraq | Sân vận động Basra |
| 06/09/2024 | 19:00 | Philippines | Sân Mỹ Đình, Hà Nội |
| 10/10/2024 | 19:30 | Indonesia | Sân Gelora Bung Karno, Jakarta |
| 15/11/2024 | 20:00 | Thái Lan | Sân Rajamangala, Bangkok |
Lịch thi đấu vòng loại các khu vực khác
Khu vực Nam Mỹ
- 06/09/2024 - 02:00 - Brazil vs Argentina
- 07/09/2024 - 03:00 - Chile vs Uruguay
- 10/09/2024 - 04:00 - Ecuador vs Colombia
- 15/09/2024 - 03:30 - Paraguay vs Peru
Khu vực Châu Âu
- 10/09/2024 - 20:45 - Pháp vs Đức
- 11/09/2024 - 21:00 - Tây Ban Nha vs Bồ Đào Nha
- 12/09/2024 - 22:00 - Anh vs Ý
- 13/09/2024 - 23:30 - Hà Lan vs Thụy Điển
Thông tin truyền hình
Các trận đấu của đội tuyển Việt Nam sẽ được phát sóng trực tiếp trên các kênh truyền hình như VTV5, FPT Play, và HTV Thể Thao.
Nhận định trước trận đấu
Việt Nam sẽ đối đầu với những đối thủ mạnh trong khu vực. Trận đấu với Iraq là một thách thức lớn khi đội bóng Tây Á luôn có sức mạnh thể chất và kỹ thuật tốt. Tuy nhiên, đội tuyển Việt Nam đã có sự chuẩn bị kỹ lưỡng và đầy tự tin cho vòng loại này.
.png)
Lịch thi đấu FIFA World Cup 2026 khu vực châu Á
Vòng loại FIFA World Cup 2026 khu vực châu Á đã được xác định với thể thức mới nhằm chọn ra 8,5 suất tham dự. Các đội bóng tại châu Á sẽ trải qua nhiều vòng thi đấu căng thẳng với các giai đoạn từ vòng loại thứ nhất đến vòng loại thứ tư, trước khi xác định những đại diện xuất sắc nhất góp mặt tại vòng chung kết World Cup 2026.
- Vòng loại thứ nhất (12/2023 - 17/2023): 20-22 đội hạng thấp nhất châu Á thi đấu loại trực tiếp theo thể thức sân nhà - sân khách.
- Vòng loại thứ hai (11/2023 - 6/2024): 36 đội (bao gồm Việt Nam) chia vào 9 bảng, thi đấu vòng tròn 2 lượt. Hai đội đầu bảng vào vòng tiếp theo.
- Vòng loại thứ ba (9/2024 - 6/2025): 18 đội chia thành 3 bảng, thi đấu vòng tròn 2 lượt sân nhà - sân khách. Hai đội đứng đầu mỗi bảng giành vé trực tiếp.
- Vòng loại thứ tư (10-11/2025): Các đội xếp thứ ba và thứ tư của vòng loại thứ ba thi đấu vòng play-off. Hai đội đứng đầu giành vé World Cup.
- Play-off liên châu lục (2025-2026): Đội đứng thứ ba từ vòng loại thứ tư sẽ thi đấu tiếp để giành suất cuối cùng.
Đội tuyển Việt Nam, với vị thế là một trong những đội mạnh của châu Á, sẽ bắt đầu chiến dịch tại vòng loại thứ hai. Lịch thi đấu cụ thể của các trận cầu đang rất được người hâm mộ chờ đợi.
| Giai đoạn | Thời gian | Thông tin chi tiết |
|---|---|---|
| Vòng loại thứ nhất | 12/2023 - 17/2023 | Các đội xếp hạng 26-47 châu Á thi đấu theo cặp sân nhà - sân khách. |
| Vòng loại thứ hai | 11/2023 - 6/2024 | 36 đội chia thành 9 bảng, thi đấu vòng tròn sân nhà - sân khách. |
| Vòng loại thứ ba | 9/2024 - 6/2025 | 18 đội chia thành 3 bảng, 6 đội giành vé trực tiếp. |
| Vòng loại thứ tư | 10/2025 - 11/2025 | 6 đội thi đấu theo vòng tròn 1 lượt tại địa điểm tập trung. |
| Play-off liên châu lục | 2025-2026 | Đội xếp thứ ba thi đấu với đại diện từ các khu vực khác. |
Lịch thi đấu cụ thể theo giờ Việt Nam
Dưới đây là lịch thi đấu của các trận đấu tại FIFA World Cup 2022 được cập nhật theo giờ Việt Nam, giúp người hâm mộ Việt Nam dễ dàng theo dõi các trận cầu đỉnh cao mà không cần phải tính toán múi giờ phức tạp. Các trận đấu sẽ diễn ra vào nhiều khung giờ khác nhau để phục vụ đông đảo khán giả. Tất cả giờ dưới đây đều theo giờ Việt Nam.
| Ngày | Trận đấu | Giờ (Việt Nam) |
|---|---|---|
| 22/11/2022 | Argentina vs Saudi Arabia | 17:00 |
| 23/11/2022 | Pháp vs Úc | 02:00 |
| 25/11/2022 | Brazil vs Serbia | 02:00 |
| 26/11/2022 | Pháp vs Đan Mạch | 23:00 |
| 29/11/2022 | Hà Lan vs Qatar | 22:00 |
| 03/12/2022 | Vòng 1/8 | 22:00 |
| 05/12/2022 | Vòng 1/8 | 02:00 |
| 09/12/2022 | Tứ kết | 02:00 |
| 13/12/2022 | Bán kết | 02:00 |
| 18/12/2022 | Chung kết | 22:00 |
Hãy đón xem và theo dõi các trận đấu hấp dẫn theo đúng giờ Việt Nam!

Kết quả vòng loại World Cup 2026 khu vực châu Á
Vòng loại World Cup 2026 khu vực châu Á đã chính thức khởi tranh với sự tham gia của nhiều đội tuyển mạnh. Giai đoạn này được chia làm các vòng đấu, bao gồm giai đoạn sơ loại và vòng bảng. Sau đây là kết quả cập nhật của các trận đấu:
| Ngày | Trận đấu | Tỷ số |
|---|---|---|
| 12/10/2023 | Hàn Quốc vs Syria | 2-0 |
| 13/10/2023 | Việt Nam vs Malaysia | 3-1 |
| 15/10/2023 | Nhật Bản vs Saudi Arabia | 1-1 |
| 16/10/2023 | Australia vs Iraq | 4-2 |
| 17/10/2023 | Qatar vs UAE | 0-0 |
Hiện tại, các đội tuyển như Nhật Bản, Hàn Quốc và Australia đang có vị trí vững chắc trong các bảng đấu, trong khi các đội Đông Nam Á như Việt Nam và Thái Lan cũng đang thể hiện phong độ tích cực với những kết quả đáng chú ý.

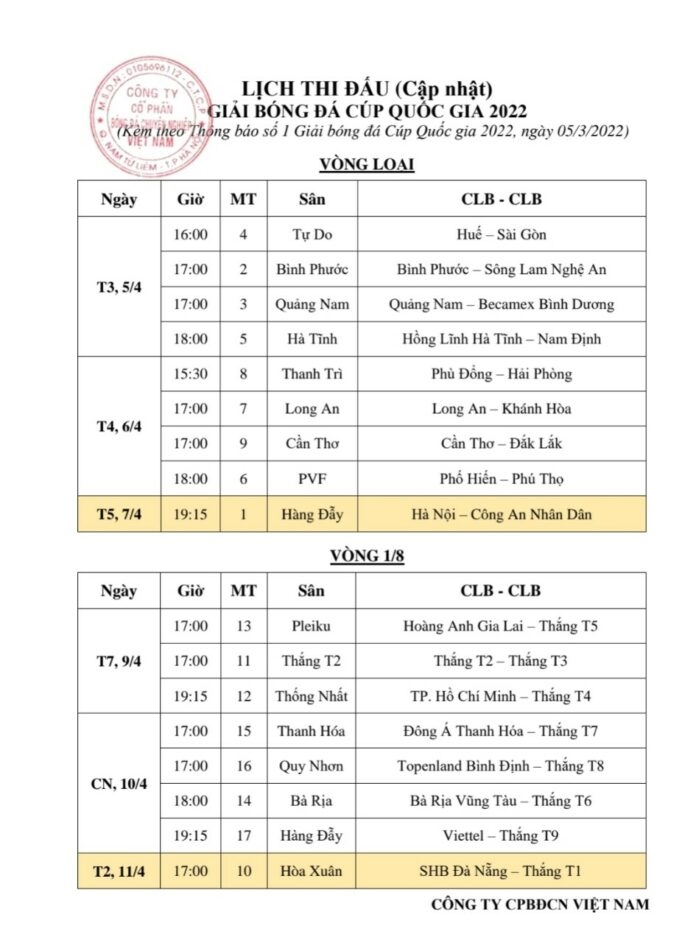
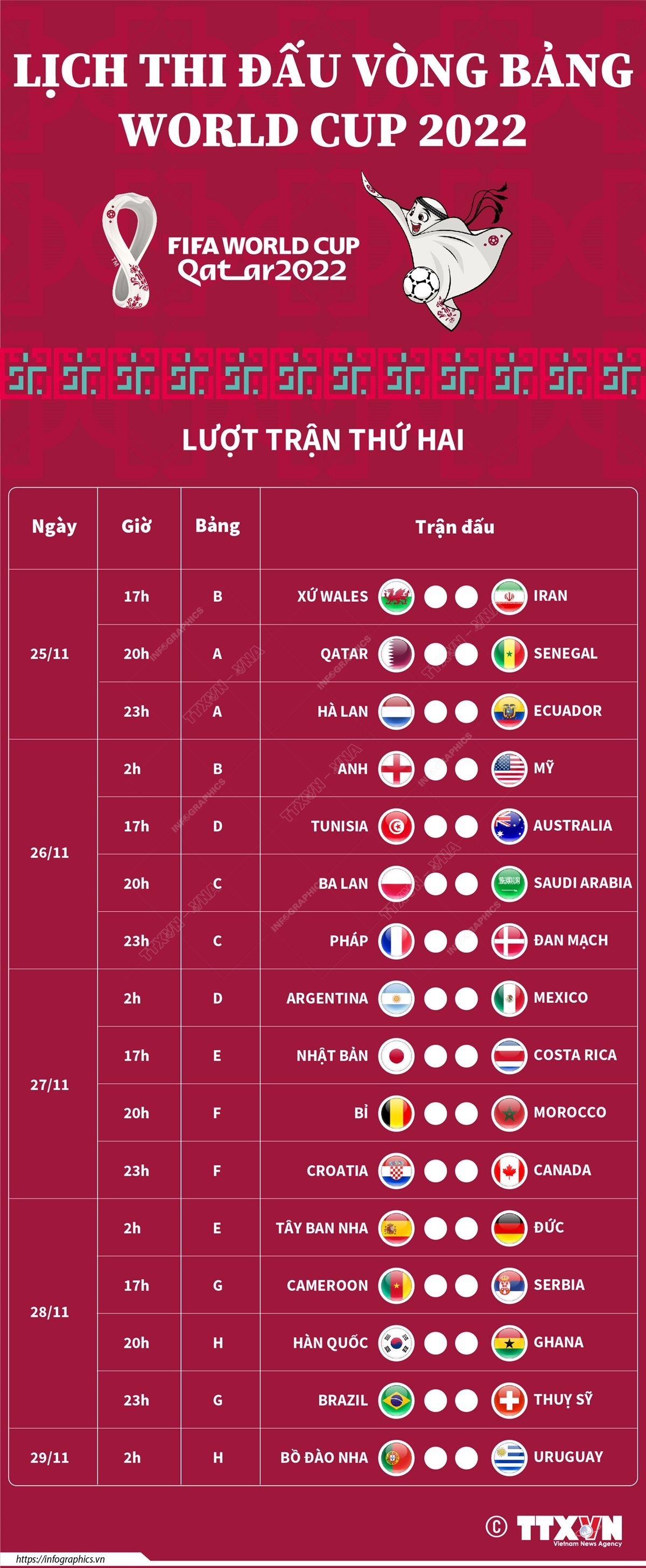
Lịch thi đấu VCK World Cup 2022
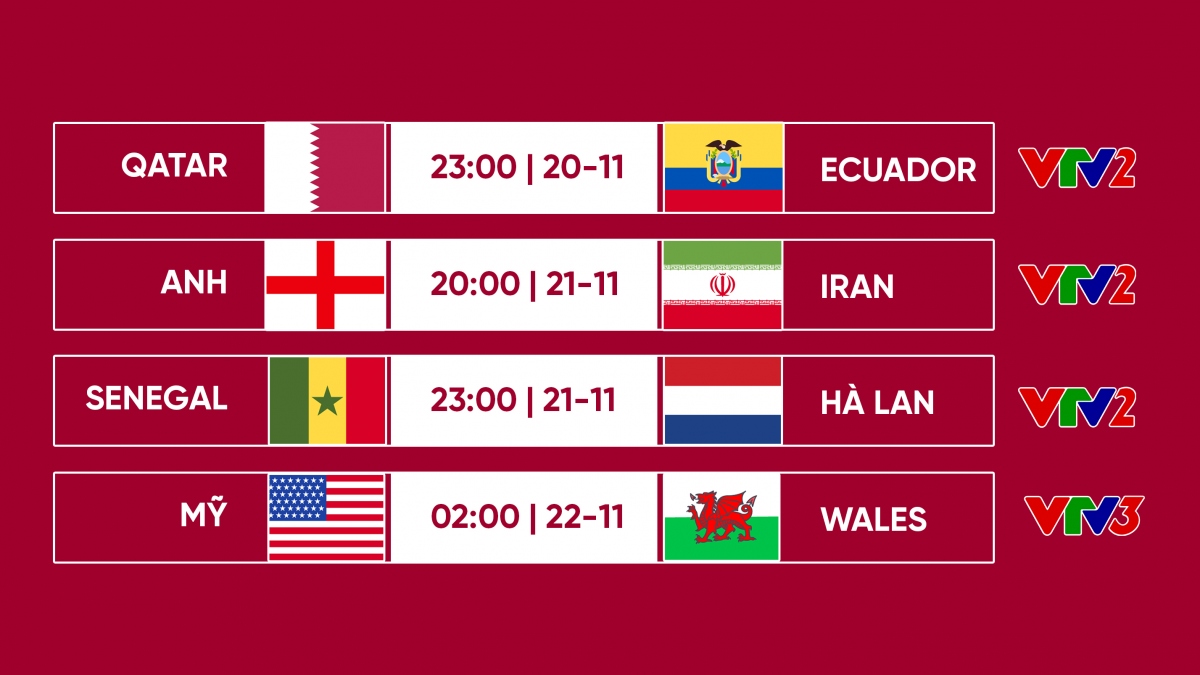
Vòng chung kết (VCK) World Cup 2022 diễn ra từ ngày 20/11 đến 18/12 tại Qatar, đây là kỳ World Cup đầu tiên được tổ chức vào mùa Đông. Dưới đây là lịch thi đấu cụ thể của các trận vòng bảng và các vòng loại trực tiếp, được tính theo giờ Việt Nam.
- Ngày khai mạc: 21/11/2022 - Trận đấu mở màn giữa đội chủ nhà Qatar và Ecuador tại sân vận động Al Bayt lúc 23h00 giờ Việt Nam.
- Vòng bảng: Diễn ra từ ngày 21/11 đến ngày 3/12. Mỗi ngày có 4 trận đấu vào các khung giờ 17h00, 20h00, 23h00, và 02h00 giờ Việt Nam.
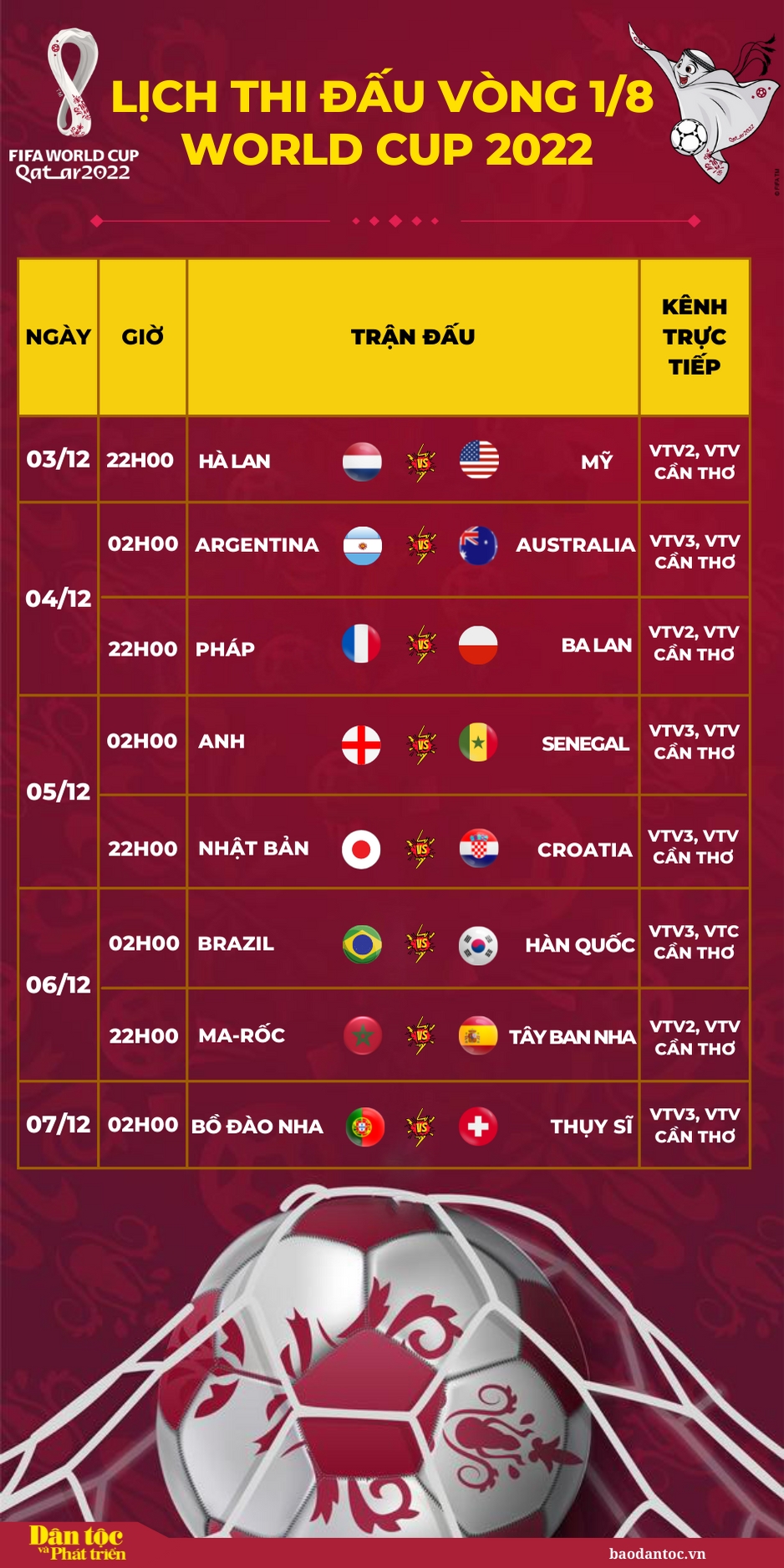
- Vòng 1/8: Bắt đầu từ ngày 3/12, các trận đấu diễn ra vào hai khung giờ 22h00 và 02h00 giờ Việt Nam.
- Trận chung kết: 18/12/2022 - Sân vận động Lusail Iconic với sức chứa 80.000 chỗ ngồi, trận đấu bắt đầu lúc 22h00 giờ Việt Nam.
Hãy theo dõi lịch thi đấu chi tiết và cập nhật theo giờ Việt Nam để không bỏ lỡ bất kỳ trận đấu nào của World Cup 2022.

10 bài tập Toán có lời giải hoàn chỉnh
-
Bài 1: Tìm giá trị của \( x \) trong phương trình \( 2x + 3 = 7 \).
Lời giải: Ta giải phương trình: \( 2x + 3 = 7 \)
\[ 2x = 7 - 3 \]
\[ 2x = 4 \]
\[ x = \frac{4}{2} = 2 \]
Vậy \( x = 2 \).
-
Bài 2: Giải hệ phương trình:
\[
\begin{cases}
3x - 2y = 7 \\
4x + y = 5
\end{cases}
\]Lời giải:
Giải phương trình thứ hai: \( y = 5 - 4x \).
Thế vào phương trình thứ nhất:
\[ 3x - 2(5 - 4x) = 7 \]
Giải tiếp:
\[ 3x - 10 + 8x = 7 \]
\[ 11x = 17 \Rightarrow x = \frac{17}{11} \]
Thế \( x \) vào phương trình \( y = 5 - 4x \) để tìm \( y \).
-
Bài 3: Tìm nghiệm của phương trình bậc hai: \( x^2 - 5x + 6 = 0 \).
Lời giải: Áp dụng công thức nghiệm:
\[ x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4 \cdot 1 \cdot 6}}{2 \cdot 1} \]
\[ x = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2} \]
\[ x = 3 \, \text{hoặc} \, x = 2 \]
-
Bài 4: Giải phương trình logarit: \( \log_2(x - 3) = 3 \).
Lời giải: Ta có:
\[ x - 3 = 2^3 \]
\[ x - 3 = 8 \Rightarrow x = 11 \]
-
Bài 5: Tính tích phân: \( \int_0^1 (x^2 + 2x) \, dx \).
Lời giải:
\[ \int_0^1 (x^2 + 2x) \, dx = \left[ \frac{x^3}{3} + x^2 \right]_0^1 \]
\[ = \left( \frac{1^3}{3} + 1^2 \right) - \left( \frac{0^3}{3} + 0^2 \right) = \frac{1}{3} + 1 = \frac{4}{3} \]
-
Bài 6: Tìm giới hạn của dãy số: \( \lim_{n \to \infty} \frac{2n^2 + 3}{n^2 + 1} \).
Lời giải:
\[ \lim_{n \to \infty} \frac{2n^2 + 3}{n^2 + 1} = \lim_{n \to \infty} \frac{n^2(2 + \frac{3}{n^2})}{n^2(1 + \frac{1}{n^2})} = 2 \]
-
Bài 7: Giải bất phương trình: \( 3x - 4 \geq 2x + 1 \).
Lời giải:
\[ 3x - 4 \geq 2x + 1 \Rightarrow x \geq 5 \]
-
Bài 8: Giải phương trình lượng giác: \( \sin x = \frac{1}{2} \).
Lời giải:
\[ x = \frac{\pi}{6} + 2k\pi \, \text{hoặc} \, x = \frac{5\pi}{6} + 2k\pi \, \text{với} \, k \in \mathbb{Z} \]
-
Bài 9: Tìm phương trình tiếp tuyến của đồ thị hàm số \( y = x^3 - 3x + 2 \) tại điểm có hoành độ \( x = 1 \).
Lời giải: Ta có đạo hàm của hàm số:
\[ y' = 3x^2 - 3 \]
Giá trị tại \( x = 1 \): \( y'(1) = 0 \). Tọa độ điểm tiếp xúc: \( (1, 0) \).
Phương trình tiếp tuyến: \( y = 0 \).
-
Bài 10: Tính chu vi của một hình tròn có bán kính \( r = 5 \).
Lời giải: Chu vi hình tròn được tính theo công thức:
\[ C = 2 \pi r = 2 \pi \cdot 5 = 10\pi \]
XEM THÊM:
Dạng bài tập 1: Giải phương trình bậc hai
Phương trình bậc hai có dạng tổng quát:
\[ ax^2 + bx + c = 0 \]
Trong đó:
- \( a, b, c \) là các hệ số, với \( a \neq 0 \).
- Ta sử dụng công thức nghiệm của phương trình bậc hai:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Ta sẽ lần lượt thực hiện các bước sau để giải phương trình:
- Bước 1: Xác định các hệ số \( a \), \( b \), \( c \) từ phương trình.
- Bước 2: Tính delta \( \Delta = b^2 - 4ac \).
- Bước 3: Dựa vào giá trị của \( \Delta \) để xác định nghiệm:
- Nếu \( \Delta > 0 \): Phương trình có 2 nghiệm phân biệt.
- Nếu \( \Delta = 0 \): Phương trình có nghiệm kép.
- Nếu \( \Delta < 0 \): Phương trình vô nghiệm.
- Bước 4: Tính nghiệm dựa trên công thức tổng quát.
Ví dụ: Giải phương trình \( 2x^2 - 4x + 1 = 0 \).
- Xác định \( a = 2 \), \( b = -4 \), \( c = 1 \).
- Tính \( \Delta = (-4)^2 - 4 \cdot 2 \cdot 1 = 16 - 8 = 8 \).
- Vì \( \Delta > 0 \), phương trình có 2 nghiệm phân biệt:
\[
x_1 = \frac{-(-4) + \sqrt{8}}{2 \cdot 2} = \frac{4 + \sqrt{8}}{4} = \frac{4 + 2\sqrt{2}}{4} = 1 + \frac{\sqrt{2}}{2}
\]
\[
x_2 = \frac{-(-4) - \sqrt{8}}{2 \cdot 2} = \frac{4 - \sqrt{8}}{4} = \frac{4 - 2\sqrt{2}}{4} = 1 - \frac{\sqrt{2}}{2}
\]
Vậy nghiệm của phương trình là \( x_1 = 1 + \frac{\sqrt{2}}{2} \) và \( x_2 = 1 - \frac{\sqrt{2}}{2} \).

Dạng bài tập 2: Tính diện tích hình tròn
Để tính diện tích hình tròn, ta sử dụng công thức:
\[ S = \pi \times r^2 \]
Trong đó:
- \( S \) là diện tích của hình tròn.
- \( r \) là bán kính của hình tròn.
- \( \pi \) là hằng số Pi (khoảng 3.14159).
Ví dụ: Tính diện tích của một hình tròn có bán kính \( r = 5 \, cm \).
Áp dụng công thức:
\[ S = \pi \times 5^2 = \pi \times 25 \approx 3.14159 \times 25 \approx 78.54 \, cm^2 \]
Vậy diện tích của hình tròn có bán kính \( 5 \, cm \) là khoảng \( 78.54 \, cm^2 \).
Lưu ý: Đơn vị diện tích là đơn vị vuông của bán kính, chẳng hạn nếu bán kính đo bằng cm thì diện tích sẽ là cm².
Các bước thực hiện:
- Xác định bán kính \( r \) của hình tròn.
- Thay giá trị của \( r \) vào công thức \( S = \pi \times r^2 \).
- Nhân hằng số Pi với bình phương của bán kính.
- Tính kết quả và ghi lại diện tích với đơn vị phù hợp.

Dạng bài tập 3: Hệ phương trình tuyến tính
Hệ phương trình tuyến tính là một tập hợp các phương trình có dạng:
Trong đó, \(x\), \(y\), và \(z\) là các biến số; \(a_1, a_2, a_3, b_1, b_2, b_3, c_1, c_2, c_3\) là các hệ số; và \(d_1, d_2, d_3\) là các hằng số.
Bước 1: Viết dạng ma trận của hệ phương trình
Đầu tiên, chúng ta biểu diễn hệ phương trình tuyến tính dưới dạng ma trận:
Ma trận hệ số là:
Ma trận các biến là:
Ma trận kết quả là:
Bước 2: Giải hệ phương trình
Có nhiều phương pháp để giải hệ phương trình tuyến tính, bao gồm:
- Phương pháp thế
- Phương pháp cộng đại số
- Phương pháp sử dụng ma trận nghịch đảo, nếu ma trận \(A\) khả nghịch.
Ví dụ, nếu ma trận \(A\) khả nghịch, nghiệm của hệ phương trình có thể được tìm bằng công thức:
Trong đó, \(A^{-1}\) là ma trận nghịch đảo của \(A\).
Bước 3: Phân tích kết quả
Sau khi giải hệ phương trình, chúng ta phân tích kết quả:
- Nếu hệ có một nghiệm duy nhất, thì ma trận \(A\) là khả nghịch và hệ phương trình có nghiệm là \((x, y, z)\).
- Nếu hệ có vô số nghiệm, thì ma trận \(A\) không khả nghịch và các phương trình có thể phụ thuộc tuyến tính vào nhau.
- Nếu hệ vô nghiệm, thì ma trận \(A\) không khả nghịch và các phương trình có thể mâu thuẫn với nhau.
Ví dụ cụ thể
Xét hệ phương trình sau:
Ta có thể giải bằng cách sử dụng phương pháp thế hoặc phương pháp ma trận như đã hướng dẫn ở trên để tìm giá trị của \(x\), \(y\), và \(z\).
Ví dụ thực tế
Giả sử bạn là người quản lý của một cửa hàng bán áo, quần và giày. Bạn biết rằng tổng số tiền bán được từ 3 mặt hàng này trong ngày hôm qua là 10 triệu đồng, với giá mỗi chiếc áo là 200 nghìn đồng, mỗi chiếc quần là 300 nghìn đồng, và mỗi đôi giày là 500 nghìn đồng. Bạn cũng biết rằng số lượng áo bán được nhiều gấp đôi số lượng quần, và tổng số lượng quần và giày bán được là 30 món. Hãy tìm số lượng áo, quần và giày đã bán được trong ngày hôm qua.
Gọi số lượng áo, quần, và giày lần lượt là \(x\), \(y\), và \(z\). Ta có hệ phương trình sau:
Bằng cách giải hệ phương trình này, bạn sẽ tìm được số lượng áo, quần và giày đã bán được.
Dạng bài tập 4: Đạo hàm và ứng dụng
Đạo hàm là một trong những khái niệm quan trọng nhất trong giải tích, với nhiều ứng dụng thực tế trong các lĩnh vực như vật lý, kinh tế, và kỹ thuật. Bài tập về đạo hàm không chỉ giúp củng cố kiến thức cơ bản mà còn giúp bạn áp dụng vào các tình huống thực tế.
1. Khái niệm cơ bản về đạo hàm
Đạo hàm của một hàm số tại một điểm thể hiện tốc độ thay đổi của hàm số tại điểm đó. Nó được định nghĩa bằng giới hạn:
Nếu giới hạn này tồn tại, hàm số \(f(x)\) được gọi là khả vi tại \(x\) và \(f'(x)\) là đạo hàm của hàm số tại điểm đó.
2. Các quy tắc đạo hàm cơ bản
- Quy tắc tổng: \(\left( f(x) + g(x) \right)' = f'(x) + g'(x)\)
- Quy tắc tích: \(\left( f(x) \cdot g(x) \right)' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\)
- Quy tắc thương: \(\left( \frac{f(x)}{g(x)} \right)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}\)
- Quy tắc chuỗi: \(\left( f(g(x)) \right)' = f'(g(x)) \cdot g'(x)\)
3. Ví dụ thực tế
Giả sử bạn là một huấn luyện viên bóng đá và muốn phân tích tốc độ chạy của các cầu thủ trong một trận đấu. Tốc độ này có thể được biểu diễn bằng hàm số \(s(t)\), với \(t\) là thời gian. Đạo hàm của \(s(t)\), ký hiệu là \(s'(t)\), sẽ cho bạn biết tốc độ thay đổi của vận tốc của cầu thủ tại thời điểm \(t\). Ví dụ:
Đạo hàm của \(s(t)\) sẽ là:
Điều này có nghĩa là tại mỗi thời điểm \(t\), tốc độ thay đổi của vận tốc của cầu thủ sẽ là \(10t + 2\) mét/giây.
4. Ứng dụng trong kinh tế
Trong kinh tế học, đạo hàm cũng được sử dụng để phân tích tốc độ tăng trưởng của lợi nhuận, doanh thu hay chi phí. Chẳng hạn, nếu hàm số \(R(x)\) biểu diễn doanh thu khi bán \(x\) sản phẩm, thì đạo hàm của \(R(x)\), ký hiệu là \(R'(x)\), sẽ cho biết tốc độ thay đổi của doanh thu khi số lượng sản phẩm thay đổi.
5. Bài tập tự luyện
- Tính đạo hàm của các hàm số sau đây:
- \(f(x) = 3x^3 - 5x + 4\)
- \(g(x) = \sin(x) + x \cdot \cos(x)\)
- \(h(x) = \ln(x^2 + 1)\)
- Cho hàm số chi phí \(C(x) = x^3 - 4x + 10\), tính đạo hàm và giải thích ý nghĩa của nó trong kinh tế.
Dạng bài tập 5: Tính tích phân cơ bản
Trong Toán học, tích phân là một công cụ quan trọng để tính toán diện tích dưới đường cong của một hàm số. Dưới đây là một số ví dụ về bài tập tính tích phân cơ bản, được giải thích chi tiết từng bước để giúp bạn hiểu rõ hơn về cách thực hiện.
Ví dụ 1: Tính tích phân của hàm số bậc nhất
Giải tích phân sau:
\[\int (2x + 3) \, dx\]
Bước 1: Xác định hàm số cần tích phân và áp dụng công thức tích phân cơ bản:
- \[\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\]
Bước 2: Áp dụng công thức cho từng hạng tử:
- \[\int 2x \, dx = 2 \cdot \frac{x^{1+1}}{1+1} = x^2\]
- \[\int 3 \, dx = 3x\]
Bước 3: Kết hợp các kết quả:
- \[\int (2x + 3) \, dx = x^2 + 3x + C\]
Ví dụ 2: Tính tích phân của hàm số bậc hai
Giải tích phân sau:
\[\int (x^2 - 4x + 4) \, dx\]
Bước 1: Tách riêng từng hạng tử để tính tích phân:
- \[\int x^2 \, dx = \frac{x^{2+1}}{2+1} = \frac{x^3}{3}\]
- \[\int -4x \, dx = -4 \cdot \frac{x^{1+1}}{1+1} = -2x^2\]
- \[\int 4 \, dx = 4x\]
Bước 2: Tổng hợp các kết quả:
- \[\int (x^2 - 4x + 4) \, dx = \frac{x^3}{3} - 2x^2 + 4x + C\]
Ví dụ 3: Tính tích phân với hằng số
Giải tích phân sau:
\[\int 5 \, dx\]
Bước 1: Hằng số được tính tích phân như sau:
- \[\int 5 \, dx = 5x + C\]
Bài tập luyện tập
- Giải tích phân sau: \(\int (3x^2 + 7x + 2) \, dx\)
- Tính tích phân của hàm số: \(\int (x^3 - 2x + 5) \, dx\)
- Giải tích phân: \(\int (4 - 2x^2) \, dx\)
Bạn hãy thử giải các bài tập trên và đối chiếu với đáp án để nắm vững hơn về phương pháp tính tích phân cơ bản.
Dạng bài tập 6: Bài tập về vectơ
Trong chương trình Toán học phổ thông, vectơ là một chủ đề quan trọng với nhiều ứng dụng trong cả lý thuyết và thực tế. Dưới đây là các bài tập phổ biến giúp học sinh nắm vững khái niệm và cách thức tính toán liên quan đến vectơ.
-
Bài tập 1: Cho hai vectơ \(\vec{u} = (3, -2)\) và \(\vec{v} = (-1, 4)\). Tính các vectơ sau:
- \(\vec{u} + \vec{v}\)
- \(\vec{u} - \vec{v}\)
- \(2\vec{u} + 3\vec{v}\)
Giải:
- \(\vec{u} + \vec{v} = (3 + (-1), -2 + 4) = (2, 2)\)
- \(\vec{u} - \vec{v} = (3 - (-1), -2 - 4) = (4, -6)\)
- \(2\vec{u} + 3\vec{v} = 2(3, -2) + 3(-1, 4) = (6, -4) + (-3, 12) = (3, 8)\)
-
Bài tập 2: Tính độ dài của vectơ \(\vec{a} = (x_1, y_1)\) và \(\vec{b} = (x_2, y_2)\). Sử dụng công thức:
\[ |\vec{a}| = \sqrt{x_1^2 + y_1^2} \] \[ |\vec{b}| = \sqrt{x_2^2 + y_2^2} \]Ví dụ: Tính độ dài của vectơ \(\vec{a} = (3, 4)\).
- \(|\vec{a}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
-
Bài tập 3: Cho hai vectơ \(\vec{a}\) và \(\vec{b}\) với \(\vec{a} = (2, -3)\) và \(\vec{b} = (-5, 4)\). Tính tích vô hướng của hai vectơ:
\[ \vec{a} \cdot \vec{b} = x_1x_2 + y_1y_2 \]Giải: \(\vec{a} \cdot \vec{b} = 2(-5) + (-3)(4) = -10 - 12 = -22\)
-
Bài tập 4: Xác định góc giữa hai vectơ \(\vec{u} = (1, 2)\) và \(\vec{v} = (2, 3)\) bằng công thức:
\[ \cos \theta = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}| |\vec{v}|} \]Giải:
- \(\vec{u} \cdot \vec{v} = 1 \cdot 2 + 2 \cdot 3 = 2 + 6 = 8\)
- \(|\vec{u}| = \sqrt{1^2 + 2^2} = \sqrt{5}\)
- \(|\vec{v}| = \sqrt{2^2 + 3^2} = \sqrt{13}\)
- \(\cos \theta = \frac{8}{\sqrt{5} \cdot \sqrt{13}} = \frac{8}{\sqrt{65}}\)
- Vậy góc \(\theta\) giữa hai vectơ là \(\theta = \cos^{-1} \left(\frac{8}{\sqrt{65}}\right)\)
-
Bài tập 5: Xác định vectơ đơn vị của vectơ \(\vec{a} = (x, y)\). Công thức để tính vectơ đơn vị là:
\[ \vec{e} = \frac{\vec{a}}{|\vec{a}|} \]Ví dụ: Tìm vectơ đơn vị của \(\vec{a} = (6, 8)\).
- Độ dài của \(\vec{a}\): \(|\vec{a}| = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\)
- Vectơ đơn vị: \(\vec{e} = \frac{(6, 8)}{10} = \left(\frac{6}{10}, \frac{8}{10}\right) = \left(\frac{3}{5}, \frac{4}{5}\right)\)
Dạng bài tập 7: Phương trình đường thẳng trong mặt phẳng
Trong toán học, phương trình đường thẳng trong mặt phẳng có thể được biểu diễn dưới nhiều dạng khác nhau. Chúng ta sẽ lần lượt khám phá các dạng này và cách áp dụng vào bài tập cụ thể.
1. Phương trình tổng quát của đường thẳng
Phương trình tổng quát của một đường thẳng trong mặt phẳng có dạng:
\( Ax + By + C = 0 \)
Trong đó:
- \( A, B, C \) là các hằng số, với \( A \) và \( B \) không đồng thời bằng 0.
- \( (x, y) \) là tọa độ của một điểm bất kỳ trên đường thẳng.
2. Phương trình tham số của đường thẳng
Phương trình tham số mô tả đường thẳng thông qua một điểm và một vector chỉ phương, có dạng:
\[
\begin{cases}
x = x_0 + at \\
y = y_0 + bt
\end{cases}
\]
Trong đó:
- \( (x_0, y_0) \) là tọa độ của một điểm trên đường thẳng.
- \( \mathbf{v} = (a, b) \) là vector chỉ phương của đường thẳng.
- \( t \) là tham số.
3. Phương trình đường thẳng đi qua hai điểm
Giả sử đường thẳng đi qua hai điểm \( A(x_1, y_1) \) và \( B(x_2, y_2) \), phương trình của đường thẳng có thể được viết dưới dạng:
\[
\frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1}
\]
Hoặc, phương trình trên có thể viết lại dưới dạng phương trình tổng quát:
\[
(y_2 - y_1)x - (x_2 - x_1)y + (x_2y_1 - x_1y_2) = 0
\]
4. Phương trình đường thẳng song song và vuông góc
Nếu hai đường thẳng song song với nhau, thì hệ số góc của chúng bằng nhau. Giả sử phương trình của hai đường thẳng là:
\( y = m_1x + c_1 \) và \( y = m_2x + c_2 \)
Hai đường thẳng này song song nếu:
\( m_1 = m_2 \)
Ngược lại, hai đường thẳng vuông góc nếu tích của hệ số góc của chúng bằng -1:
\( m_1 \times m_2 = -1 \)
5. Bài tập ứng dụng
Hãy áp dụng những kiến thức trên vào bài tập sau:
- Viết phương trình của đường thẳng đi qua hai điểm \( A(1, 2) \) và \( B(3, 4) \).
- Cho đường thẳng \( y = 2x + 1 \). Viết phương trình của đường thẳng song song và đường thẳng vuông góc với nó đi qua điểm \( C(0, -1) \).
- Xác định phương trình của đường thẳng đi qua điểm \( D(2, 3) \) và có hệ số góc \( m = -2 \).
Hãy thực hiện từng bước tính toán để tìm ra phương trình chính xác của các đường thẳng này.

Dạng bài tập 8: Xác suất và thống kê
Trong dạng bài tập này, chúng ta sẽ tìm hiểu cách tính xác suất và các ứng dụng của thống kê trong giải quyết các bài toán thực tế. Xác suất là một khái niệm cơ bản trong toán học, dùng để đo lường mức độ xảy ra của một sự kiện. Thống kê giúp chúng ta thu thập, phân tích và diễn giải dữ liệu để đưa ra các kết luận hữu ích.
Bài tập 1: Tính xác suất đơn giản
Xác suất của một sự kiện \( A \) xảy ra được tính bằng công thức:
\[
P(A) = \frac{\text{số trường hợp thuận lợi}}{\text{tổng số trường hợp có thể xảy ra}}
\]
- Xét một hộp có 3 quả bóng đỏ và 2 quả bóng xanh. Tính xác suất để rút được một quả bóng đỏ.
- Giả sử bạn tung một đồng xu hai lần. Tính xác suất để cả hai lần đều xuất hiện mặt ngửa.
Bài tập 2: Xác suất có điều kiện
Xác suất có điều kiện của sự kiện \( A \) xảy ra khi biết sự kiện \( B \) đã xảy ra được tính bằng công thức:
\[
P(A|B) = \frac{P(A \cap B)}{P(B)}
\]
- Một hộp có 5 quả bóng đỏ và 3 quả bóng xanh. Nếu rút ngẫu nhiên một quả bóng và không trả lại, sau đó rút tiếp quả bóng thứ hai, tính xác suất để cả hai quả bóng được rút ra đều là màu đỏ.
- Trong một lớp học có 10 nam và 15 nữ, chọn ngẫu nhiên 2 học sinh. Tính xác suất để cả hai học sinh được chọn đều là nữ.
Bài tập 3: Thống kê mô tả
Thống kê mô tả giúp tóm tắt và mô tả dữ liệu bằng các chỉ số như trung bình, trung vị, phương sai và độ lệch chuẩn. Ví dụ, cho dữ liệu về điểm số của học sinh trong một bài kiểm tra:
\[
7, 8, 6, 5, 9, 7, 8, 7, 6, 5
\]
Hãy tính:
- Giá trị trung bình: \(\bar{x} = \frac{\sum x_i}{n}\)
- Phương sai: \(Var(x) = \frac{\sum (x_i - \bar{x})^2}{n}\)
- Độ lệch chuẩn: \(\sigma = \sqrt{Var(x)}\)
Dạng bài tập 9: Giải hệ bất phương trình
Giải hệ bất phương trình là một trong những kỹ năng quan trọng trong toán học, giúp xác định tập hợp các giá trị thỏa mãn đồng thời nhiều bất phương trình. Để giải hệ bất phương trình, ta cần thực hiện các bước cơ bản sau:
- Biểu diễn từng bất phương trình:
Hệ bất phương trình gồm nhiều bất phương trình, mỗi bất phương trình cần được biểu diễn dưới dạng tổng quát như:
\[ ax + b > 0 \]
\[ cx + d \leq 0 \]
- Tìm nghiệm của từng bất phương trình:
Giải từng bất phương trình riêng lẻ để tìm nghiệm của nó. Ví dụ:
- Với bất phương trình \[ ax + b > 0 \], ta có nghiệm là \[ x > -\frac{b}{a} \] nếu \( a > 0 \), hoặc \[ x < -\frac{b}{a} \] nếu \( a < 0 \).
- Với bất phương trình \[ cx + d \leq 0 \], ta có nghiệm là \[ x \leq -\frac{d}{c} \] nếu \( c > 0 \), hoặc \[ x \geq -\frac{d}{c} \] nếu \( c < 0 \).
- Biểu diễn nghiệm trên trục số:
Sau khi tìm được nghiệm của từng bất phương trình, ta biểu diễn chúng trên cùng một trục số để xác định tập nghiệm chung của hệ.
Ví dụ, nếu nghiệm của hai bất phương trình là:
- \[ x > -2 \]
- \[ x \leq 3 \]
Thì tập nghiệm chung sẽ là \[ -2 < x \leq 3 \].
- Viết tập nghiệm:
Tập nghiệm của hệ bất phương trình là giao của các tập nghiệm của từng bất phương trình. Trong ví dụ trên, ta có:
\[ S = \{ x \mid -2 < x \leq 3 \} \]
Khi giải hệ bất phương trình, cần lưu ý đến các trường hợp đặc biệt, chẳng hạn như bất phương trình vô nghiệm hoặc có nghiệm là mọi số thực. Bằng cách nắm vững các bước trên, bạn sẽ dễ dàng giải quyết được các bài tập liên quan đến hệ bất phương trình.
Dạng bài tập 10: Tính thể tích khối chóp
Trong hình học không gian, tính thể tích khối chóp là một dạng bài tập phổ biến và quan trọng. Dưới đây là các bước cơ bản và công thức tính thể tích khối chóp mà bạn cần nắm vững:
- Nhận diện khối chóp:
Một khối chóp được tạo thành từ một đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh. Đỉnh này không nằm trong mặt phẳng chứa đáy.
- Công thức tính thể tích khối chóp:
Thể tích \( V \) của khối chóp được tính bằng công thức:
\[ V = \frac{1}{3} S_h \times h \]
Trong đó:
- \( S_h \): Diện tích đáy của khối chóp.
- \( h \): Chiều cao của khối chóp, là khoảng cách từ đỉnh đến mặt phẳng chứa đáy.
- Ví dụ minh họa:
Xét một khối chóp có đáy là hình tam giác với diện tích đáy \( S_h = 20 \, cm^2 \) và chiều cao từ đỉnh đến mặt phẳng đáy là \( h = 15 \, cm \). Thể tích của khối chóp này được tính như sau:
\[ V = \frac{1}{3} \times 20 \, cm^2 \times 15 \, cm = 100 \, cm^3 \]
- Lưu ý khi giải bài tập:
- Đảm bảo đo đạc đúng các yếu tố như chiều cao và diện tích đáy.
- Chú ý tới đơn vị đo lường, cần thống nhất đơn vị trước khi áp dụng công thức.
- Khi bài toán phức tạp hơn, có thể cần sử dụng các phương pháp phân tích thêm, như chia khối chóp thành các phần nhỏ hơn hoặc áp dụng định lý về thể tích các hình khối phức hợp.
Việc hiểu và áp dụng đúng công thức sẽ giúp bạn dễ dàng giải quyết các bài tập liên quan đến tính thể tích khối chóp trong các bài kiểm tra và kỳ thi.