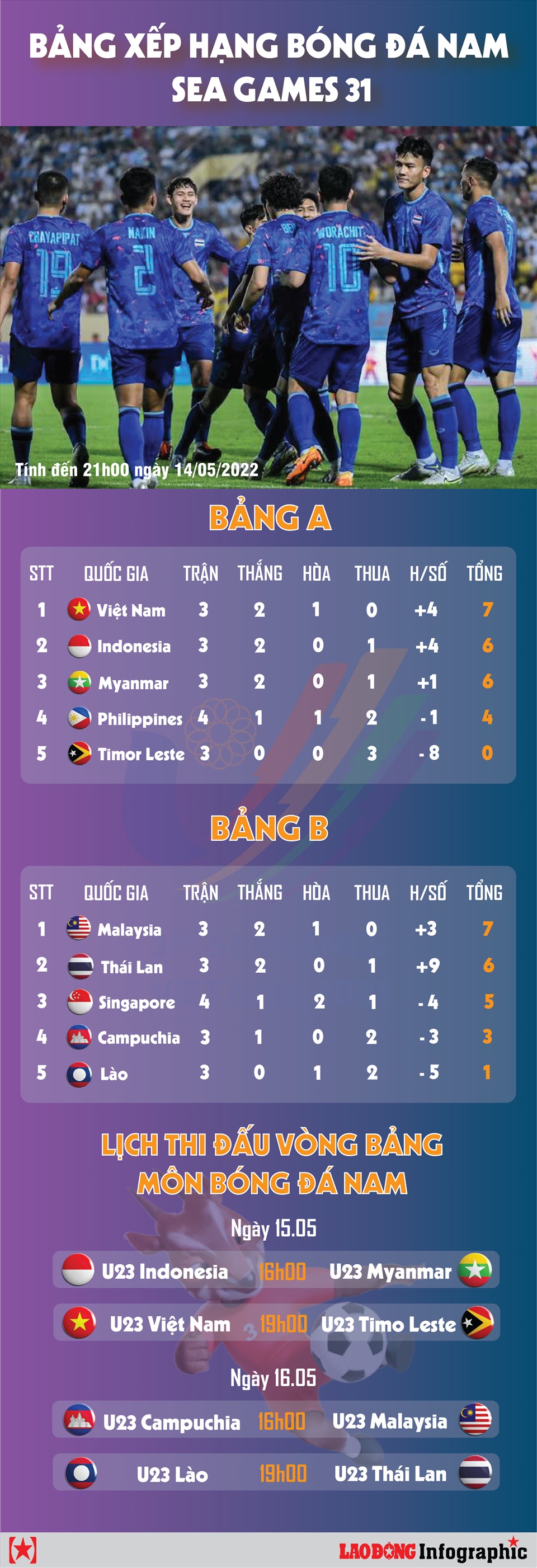
Chủ đề xếp hạng thế giới bóng đá nam: Xếp hạng thế giới bóng đá nam luôn thu hút sự quan tâm lớn của người hâm mộ, đặc biệt là khi có những biến động bất ngờ. Bài viết này sẽ cung cấp thông tin cập nhật mới nhất về bảng xếp hạng FIFA, cùng với những phân tích sâu sắc về vị trí của đội tuyển Việt Nam và các đội tuyển hàng đầu thế giới.
Mục lục
- Bảng xếp hạng thế giới bóng đá nam
- Mục lục tổng hợp
- Bài tập Tiếng Anh với lời giải
- Bài tập Toán học với lời giải
- Bài tập Vật lý với lời giải
- Bài tập Toán nâng cao
- Bài tập về cấu trúc ngữ pháp Tiếng Anh
- Bài tập về động lực học
- Bài tập Tiếng Anh giao tiếp
- Bài tập về giải tích cơ bản
- Bài tập về cơ học chất lỏng
- Bài tập về xác suất thống kê
Bảng xếp hạng thế giới bóng đá nam
Bảng xếp hạng thế giới bóng đá nam được FIFA công bố thường xuyên, cung cấp thông tin về thứ hạng của các đội tuyển quốc gia dựa trên kết quả thi đấu trong các giải đấu quốc tế. Dưới đây là một số thông tin chi tiết về thứ hạng của các đội tuyển trên thế giới và tại Việt Nam.
Bảng xếp hạng FIFA tháng 7/2024
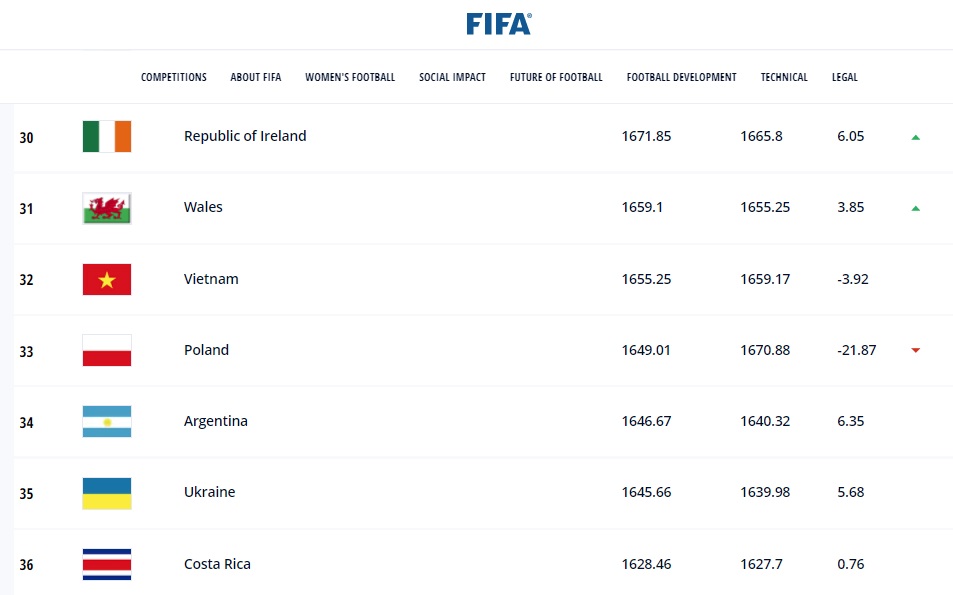
- Việt Nam: Đội tuyển Việt Nam đã thăng 1 bậc để xếp hạng 115 thế giới với 1.168,02 điểm. Sự thăng hạng này là kết quả của việc các đội tuyển khác bị trừ điểm và tụt hạng.
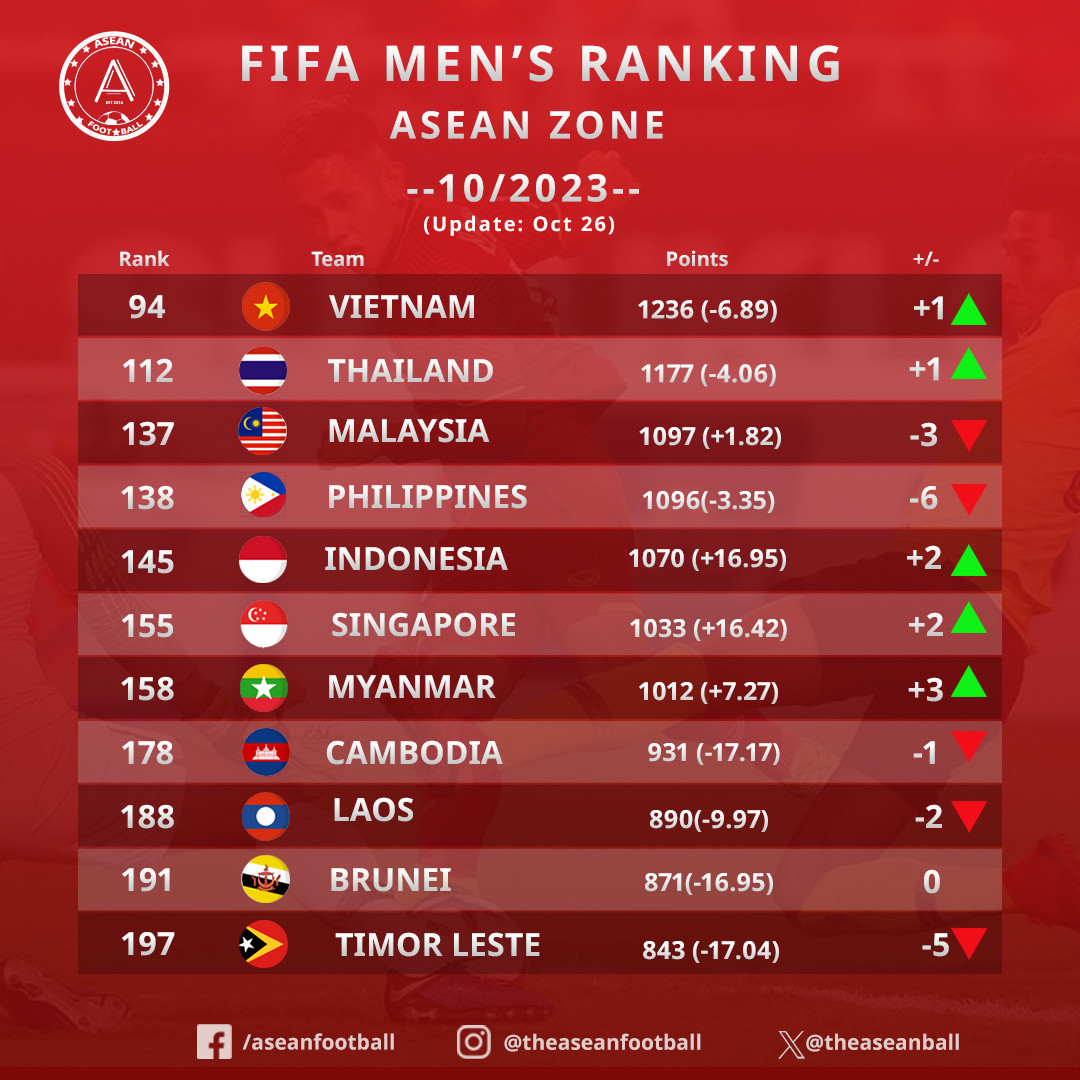
- Khu vực Đông Nam Á: Thái Lan dẫn đầu khu vực nhưng đã tụt hạng ra khỏi top 100, trong khi Indonesia tăng 1 bậc lên vị trí 133, xếp ngay trên Malaysia.
- Châu Á: Nhật Bản dẫn đầu khu vực châu Á, tiếp theo là Iran và Hàn Quốc.
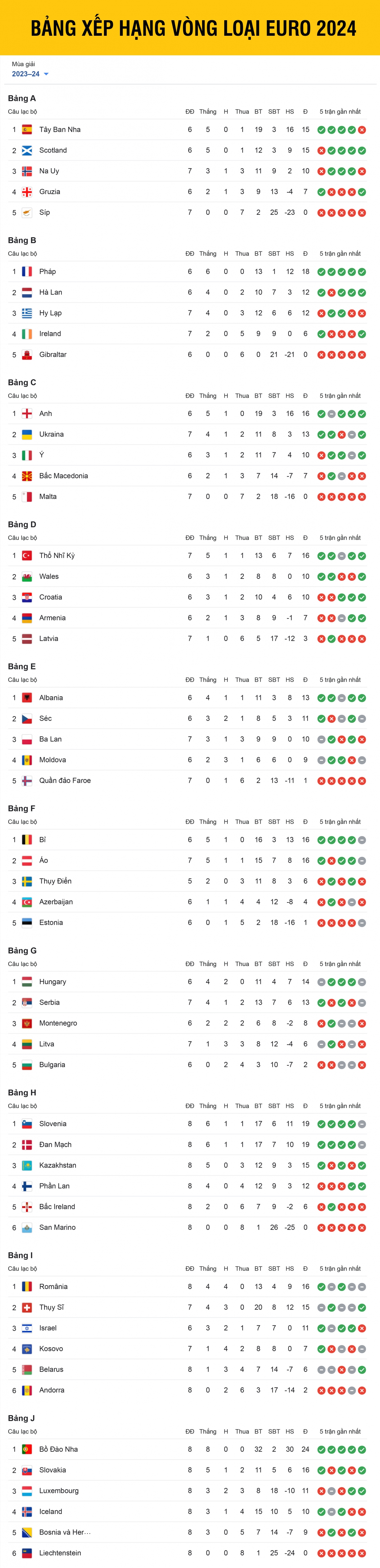
- Thế giới: Argentina tiếp tục dẫn đầu sau khi giành chức vô địch Copa America 2024. Tây Ban Nha thăng 5 bậc để xếp hạng 3 sau khi vô địch EURO 2024.
Các thay đổi đáng chú ý
- Tụt hạng: Đội tuyển Việt Nam đã từng tụt 10 bậc trong tháng 4/2024 xuống vị trí thứ 115 thế giới do thất bại trước Indonesia tại vòng loại World Cup 2026.
- Điểm số: Thứ hạng của Việt Nam bị ảnh hưởng do bị trừ tới 30,04 điểm sau các trận thua trước Indonesia.
Đánh giá tổng quan
Bảng xếp hạng FIFA là công cụ quan trọng để đánh giá sự tiến bộ của các đội tuyển quốc gia trong bóng đá thế giới. Với thứ hạng hiện tại, đội tuyển Việt Nam vẫn giữ vững vị trí trong top các đội mạnh nhất khu vực Đông Nam Á, đồng thời tiếp tục nỗ lực cải thiện thành tích trên bảng xếp hạng thế giới.

.png)
Mục lục tổng hợp
Trong mục lục tổng hợp này, chúng ta sẽ đi qua các khía cạnh quan trọng và chi tiết nhất liên quan đến bảng xếp hạng thế giới bóng đá nam, từ thông tin cơ bản đến phân tích chuyên sâu. Mục tiêu là cung cấp cho người đọc cái nhìn toàn diện về chủ đề này.
- Giới thiệu về bảng xếp hạng FIFA
- Khái niệm và vai trò của bảng xếp hạng FIFA trong bóng đá quốc tế.
- Phương pháp tính điểm và cập nhật thứ hạng.
- Cập nhật thứ hạng đội tuyển Việt Nam
- Thứ hạng hiện tại của đội tuyển Việt Nam trên bảng xếp hạng FIFA.
- Các yếu tố ảnh hưởng đến thứ hạng của đội tuyển Việt Nam.
- Lịch sử thăng trầm của đội tuyển Việt Nam qua các thời kỳ.
- Phân tích thứ hạng khu vực Đông Nam Á
- So sánh thứ hạng giữa các đội tuyển trong khu vực Đông Nam Á.
- Đánh giá tiềm năng của các đội tuyển trong khu vực.
- Top 10 đội tuyển quốc gia dẫn đầu bảng xếp hạng FIFA
- Danh sách top 10 đội tuyển quốc gia có thứ hạng cao nhất.
- Phân tích sức mạnh và chiến thuật của các đội tuyển này.
- Biến động thứ hạng của các đội tuyển qua các giải đấu lớn
- Ảnh hưởng của các giải đấu như World Cup, Euro đến thứ hạng FIFA.
- Các trường hợp tụt hạng hoặc thăng hạng đáng chú ý.
- Dự báo và nhận định về thứ hạng trong tương lai
- Dự đoán những thay đổi trong bảng xếp hạng FIFA sau các giải đấu sắp tới.
- Nhận định về khả năng cải thiện thứ hạng của đội tuyển Việt Nam.
- Ứng dụng của bảng xếp hạng FIFA trong nghiên cứu bóng đá
- Cách sử dụng bảng xếp hạng FIFA để đánh giá và phân tích các đội tuyển.
- Những nghiên cứu nổi bật dựa trên bảng xếp hạng FIFA.
- Kết luận và tầm quan trọng của bảng xếp hạng FIFA
- Vai trò của bảng xếp hạng FIFA trong việc thúc đẩy sự phát triển của bóng đá toàn cầu.
- Những tác động đến hình ảnh và sự nghiệp của các đội tuyển và cầu thủ.
Bài tập Tiếng Anh với lời giải
Dưới đây là một số bài tập Tiếng Anh với lời giải chi tiết, giúp bạn nắm vững các khía cạnh ngữ pháp, từ vựng và kỹ năng đọc hiểu trong Tiếng Anh. Các bài tập này được thiết kế để phát triển khả năng sử dụng Tiếng Anh một cách chính xác và tự tin.
- Bài tập 1: Chia động từ trong ngoặc
Điền vào chỗ trống với dạng đúng của động từ trong ngoặc.
Ví dụ: If I (know) the answer, I (tell) you.
Lời giải: knew, would tell
- Bài tập 2: Chọn đáp án đúng
Chọn đáp án đúng cho các câu sau:
1. She ___ to the store yesterday. (go, goes, went)
2. They ___ playing football now. (is, are, were)
Lời giải:
- 1. went
- 2. are
- Bài tập 3: Viết lại câu
Viết lại các câu sau sao cho nghĩa không thay đổi:
1. I have never seen such a beautiful painting before.
Lời giải: This is the most beautiful painting I have ever seen.
- Bài tập 4: Hoàn thành đoạn văn
Điền từ phù hợp vào chỗ trống trong đoạn văn sau:
The weather was very ___ (1) yesterday. We decided to go for a ___ (2) in the park. It was a ___ (3) idea as we enjoyed the fresh air.
Lời giải:
- 1. nice
- 2. walk
- 3. great
- Bài tập 5: Chọn từ đúng
Chọn từ đúng để hoàn thành câu:
1. I want to ___ (learn, study) English.
2. She is ___ (good, well) at playing the piano.
Lời giải:
- 1. learn
- 2. good
- Bài tập 6: Đọc hiểu
Đọc đoạn văn và trả lời các câu hỏi bên dưới:
Đoạn văn: "Last summer, I went to the beach with my family. We had a lot of fun swimming and building sandcastles..."
Câu hỏi: Where did the author go last summer?
Lời giải: The author went to the beach.
- Bài tập 7: Chia câu thành các phần
Phân tích cấu trúc ngữ pháp của câu sau:
"She gave me a book that she had read."
Lời giải:
- Chủ ngữ: She
- Động từ: gave
- Đối tượng: me
- Tân ngữ: a book
- Mệnh đề quan hệ: that she had read
- Bài tập 8: Điền từ vào câu
Điền từ thích hợp vào chỗ trống:
1. She is ___ (tall) than her brother.
2. They ___ (have) been to Japan twice.
Lời giải:
- 1. taller
- 2. have
- Bài tập 9: Sắp xếp câu
Sắp xếp lại các từ sau để tạo thành câu hoàn chỉnh:
1. happy / She / is / very / today.
Lời giải: She is very happy today.
- Bài tập 10: Tìm lỗi sai và sửa lỗi
Tìm và sửa lỗi sai trong các câu sau:
1. He don’t like to swim.
Lời giải: He doesn’t like to swim.

Bài tập Toán học với lời giải
Dưới đây là một số bài tập Toán học với lời giải chi tiết, giúp bạn rèn luyện và nâng cao kỹ năng toán học, từ cơ bản đến nâng cao. Mỗi bài tập được thiết kế để giúp bạn hiểu rõ hơn các khái niệm toán học quan trọng.
- Bài tập 1: Giải phương trình bậc hai
Giải phương trình bậc hai sau: \( x^2 - 5x + 6 = 0 \).
Lời giải:
Phương trình có dạng chuẩn \( ax^2 + bx + c = 0 \) với \( a = 1 \), \( b = -5 \), \( c = 6 \). Áp dụng công thức nghiệm:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]Ta có:
\[ x = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2} \]Vậy \( x_1 = 3 \), \( x_2 = 2 \).
- Bài tập 2: Tính tích phân
Tính tích phân sau: \( \int_0^1 (3x^2 + 2x) \, dx \).
Lời giải:
Áp dụng công thức tích phân:
\[ \int (ax^n) \, dx = \frac{ax^{n+1}}{n+1} \]Ta có:
\[ \int (3x^2 + 2x) \, dx = x^3 + x^2 \Big|_0^1 = (1 + 1) - (0 + 0) = 2 \] - Bài tập 3: Tính giới hạn
Tính giới hạn sau: \( \lim_{x \to \infty} \frac{2x^2 + 3x + 1}{x^2 - x + 2} \).
Lời giải:
Chia tử và mẫu cho \( x^2 \):
\[ \lim_{x \to \infty} \frac{2x^2 + 3x + 1}{x^2 - x + 2} = \lim_{x \to \infty} \frac{2 + \frac{3}{x} + \frac{1}{x^2}}{1 - \frac{1}{x} + \frac{2}{x^2}} = \frac{2}{1} = 2 \] - Bài tập 4: Tính đạo hàm
Tính đạo hàm của hàm số \( f(x) = x^3 - 3x^2 + 2x \).
Lời giải:
Áp dụng công thức đạo hàm:
\[ f'(x) = 3x^2 - 6x + 2 \] - Bài tập 5: Giải hệ phương trình
Giải hệ phương trình sau:
\[ \begin{cases} 2x + 3y = 7 \\ 4x - y = 5 \end{cases} \]Lời giải:
Nhân phương trình thứ hai với 3 và trừ đi phương trình đầu:
\[ 12x - 3y - 2x - 3y = 15 - 7 \Rightarrow 10x = 8 \Rightarrow x = \frac{4}{5} \]Thay \( x \) vào phương trình thứ nhất để tìm \( y \).
\[ 2\left(\frac{4}{5}\right) + 3y = 7 \Rightarrow y = \frac{11}{15} \] - Bài tập 6: Tính diện tích hình tròn
Tính diện tích hình tròn có bán kính \( r = 3 \) cm.
Lời giải:
Áp dụng công thức diện tích hình tròn:
\[ S = \pi r^2 = \pi (3)^2 = 9\pi \text{ cm}^2 \] - Bài tập 7: Tính căn bậc hai
Tính căn bậc hai của 49.
Lời giải:
\[ \sqrt{49} = 7 \] - Bài tập 8: Giải phương trình bậc nhất
Giải phương trình: \( 2x - 4 = 0 \).
Lời giải:
\[ 2x = 4 \Rightarrow x = 2 \] - Bài tập 9: Tính chu vi hình chữ nhật
Tính chu vi của hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.
Lời giải:
\[ P = 2(l + w) = 2(5 + 3) = 16 \text{ cm} \] - Bài tập 10: Phân tích đa thức thành nhân tử
Phân tích đa thức sau thành nhân tử: \( x^2 - 4 \).
Lời giải:
\[ x^2 - 4 = (x - 2)(x + 2) \]

Bài tập Vật lý với lời giải
Dưới đây là một số bài tập Vật lý cơ bản cùng với lời giải chi tiết, giúp bạn củng cố kiến thức và áp dụng các nguyên lý vật lý vào giải quyết các vấn đề thực tế.
- Bài tập 1: Tính lực căng dây
Một vật có khối lượng \( m = 2 \, \text{kg} \) treo vào một sợi dây không giãn. Tính lực căng dây khi vật đứng yên.
Lời giải:
Lực căng dây \( T \) cân bằng với trọng lực \( mg \):
\[ T = mg = 2 \times 9.8 = 19.6 \, \text{N} \] - Bài tập 2: Tính công cơ học
Tính công thực hiện khi một lực \( F = 50 \, \text{N} \) kéo một vật di chuyển \( s = 10 \, \text{m} \) theo phương ngang.
Lời giải:
Công cơ học được tính bằng công thức:
\[ A = F \cdot s \cdot \cos\theta \]Vì \( \theta = 0^\circ \), ta có:
\[ A = 50 \times 10 \times \cos0^\circ = 500 \, \text{J} \] - Bài tập 3: Tính vận tốc trung bình
Một ô tô di chuyển từ điểm A đến điểm B với vận tốc \( v_1 = 60 \, \text{km/h} \) và từ B về A với vận tốc \( v_2 = 40 \, \text{km/h} \). Tính vận tốc trung bình của ô tô trong cả quãng đường.
Lời giải:
Vận tốc trung bình \( v_{\text{tb}} \) được tính bằng:
\[ v_{\text{tb}} = \frac{2v_1v_2}{v_1 + v_2} = \frac{2 \times 60 \times 40}{60 + 40} = 48 \, \text{km/h} \] - Bài tập 4: Tính gia tốc
Một vật chuyển động thẳng đều với vận tốc ban đầu \( v_0 = 0 \) và gia tốc \( a = 2 \, \text{m/s}^2 \). Tính quãng đường vật đi được sau \( t = 5 \, \text{s} \).
Lời giải:
Quãng đường \( s \) được tính bằng:
\[ s = v_0t + \frac{1}{2}at^2 = 0 + \frac{1}{2} \times 2 \times 5^2 = 25 \, \text{m} \] - Bài tập 5: Tính áp suất
Một khối gỗ có diện tích đáy \( S = 0.2 \, \text{m}^2 \) đặt trên sàn, với khối lượng \( m = 50 \, \text{kg} \). Tính áp suất mà khối gỗ tác dụng lên sàn.
Lời giải:
Áp suất \( p \) được tính bằng:
\[ p = \frac{F}{S} = \frac{mg}{S} = \frac{50 \times 9.8}{0.2} = 2450 \, \text{Pa} \] - Bài tập 6: Định luật bảo toàn cơ năng
Một vật rơi tự do từ độ cao \( h = 20 \, \text{m} \). Tính vận tốc của vật khi chạm đất.
Lời giải:
Sử dụng định luật bảo toàn cơ năng:
\[ v = \sqrt{2gh} = \sqrt{2 \times 9.8 \times 20} = 19.8 \, \text{m/s} \] - Bài tập 7: Tính nhiệt lượng
Tính nhiệt lượng cần thiết để làm nóng \( m = 500 \, \text{g} \) nước từ \( 20^\circ \text{C} \) đến \( 80^\circ \text{C} \) (Biết nhiệt dung riêng của nước là \( c = 4200 \, \text{J/kg.K} \)).
Lời giải:
Nhiệt lượng \( Q \) được tính bằng:
\[ Q = mc\Delta t = 0.5 \times 4200 \times (80 - 20) = 126000 \, \text{J} \] - Bài tập 8: Tính công suất
Một động cơ thực hiện công \( A = 2000 \, \text{J} \) trong \( t = 10 \, \text{s} \). Tính công suất của động cơ.
Lời giải:
Công suất \( P \) được tính bằng:
\[ P = \frac{A}{t} = \frac{2000}{10} = 200 \, \text{W} \] - Bài tập 9: Tính động năng
Một vật có khối lượng \( m = 4 \, \text{kg} \) chuyển động với vận tốc \( v = 10 \, \text{m/s} \). Tính động năng của vật.
Lời giải:
Động năng \( W \) được tính bằng:
\[ W = \frac{1}{2}mv^2 = \frac{1}{2} \times 4 \times 10^2 = 200 \, \text{J} \] - Bài tập 10: Tính chiều dài quỹ đạo
Một vật chuyển động theo đường tròn có bán kính \( r = 2 \, \text{m} \) với vận tốc \( v = 4 \, \text{m/s} \). Tính thời gian vật đi hết một vòng tròn.
Lời giải:
Chu kỳ \( T \) được tính bằng:
\[ T = \frac{2\pi r}{v} = \frac{2 \times 3.14 \times 2}{4} = 3.14 \, \text{s} \]

Bài tập Toán nâng cao
Dưới đây là các bài tập Toán nâng cao, giúp bạn rèn luyện tư duy và kỹ năng giải quyết các bài toán phức tạp. Mỗi bài tập đi kèm với lời giải chi tiết để bạn có thể hiểu rõ cách tiếp cận và phương pháp giải.
- Bài tập 1: Giải phương trình bậc ba
Giải phương trình bậc ba sau: \( x^3 - 6x^2 + 11x - 6 = 0 \)
Lời giải:
Phương trình này có thể giải bằng cách phân tích thành nhân tử:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0 \]Vậy các nghiệm của phương trình là \( x = 1, 2, 3 \).
- Bài tập 2: Tính tích phân
Tính tích phân sau: \( \int_0^1 (3x^2 + 2x + 1) \, dx \)
Lời giải:
Sử dụng công thức tích phân cơ bản:
\[ \int (3x^2 + 2x + 1) \, dx = x^3 + x^2 + x + C \]Áp dụng giới hạn từ \( 0 \) đến \( 1 \):
\[ \int_0^1 (3x^2 + 2x + 1) \, dx = \left[ x^3 + x^2 + x \right]_0^1 = 1 + 1 + 1 = 3 \] - Bài tập 3: Giải hệ phương trình
Giải hệ phương trình sau:
\[ \begin{cases} 2x + 3y = 6 \\ 4x - y = 5 \end{cases} \]Lời giải:
Dùng phương pháp thế hoặc cộng đại số, ta tìm được:
Giải phương trình thứ hai theo \( y \):
\[ y = 4x - 5 \]Thay vào phương trình thứ nhất:
\[ 2x + 3(4x - 5) = 6 \Rightarrow 14x = 21 \Rightarrow x = \frac{21}{14} = \frac{3}{2} \]Thay \( x = \frac{3}{2} \) vào \( y = 4x - 5 \), ta được:
\[ y = 4 \times \frac{3}{2} - 5 = 6 - 5 = 1 \]Vậy nghiệm của hệ là \( x = \frac{3}{2}, y = 1 \).
- Bài tập 4: Tính giới hạn
Tính giới hạn sau: \( \lim_{x \to 0} \frac{\sin x}{x} \)
Lời giải:
Áp dụng giới hạn cơ bản trong giải tích:
\[ \lim_{x \to 0} \frac{\sin x}{x} = 1 \] - Bài tập 5: Tính chuỗi vô hạn
Tính tổng của chuỗi vô hạn: \( S = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots \)
Lời giải:
Chuỗi này là một chuỗi hình học với công bội \( q = \frac{1}{2} \), tổng của chuỗi là:
\[ S = \frac{a_1}{1-q} = \frac{1}{1-\frac{1}{2}} = 2 \] - Bài tập 6: Tính đạo hàm cấp 2
Tính đạo hàm cấp 2 của hàm số \( f(x) = x^4 - 2x^3 + x \)
Lời giải:
Tính đạo hàm cấp 1:
\[ f'(x) = 4x^3 - 6x^2 + 1 \]Đạo hàm cấp 2 là:
\[ f''(x) = 12x^2 - 12x \] - Bài tập 7: Giải bất phương trình
Giải bất phương trình: \( x^2 - 4x + 3 > 0 \)
Lời giải:
Phân tích biểu thức thành nhân tử:
\[ x^2 - 4x + 3 = (x-1)(x-3) > 0 \]Nghiệm của bất phương trình là:
\[ x < 1 \quad \text{hoặc} \quad x > 3 \] - Bài tập 8: Tính thể tích khối tròn xoay
Tính thể tích của khối tròn xoay tạo bởi đường cong \( y = x^2 \) khi quay quanh trục Ox từ \( x = 0 \) đến \( x = 1 \).
Lời giải:
Thể tích \( V \) của khối tròn xoay được tính bằng:
\[ V = \pi \int_0^1 (x^2)^2 dx = \pi \int_0^1 x^4 dx = \frac{\pi}{5} \] - Bài tập 9: Tìm giá trị lớn nhất, nhỏ nhất
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \( f(x) = x^3 - 3x^2 + 2 \) trên đoạn \( [0, 2] \).
Lời giải:
Tính đạo hàm và tìm nghiệm:
\[ f'(x) = 3x^2 - 6x \]Nghiệm là \( x = 0 \) hoặc \( x = 2 \). So sánh \( f(0) = 2 \), \( f(2) = 2 \) và \( f(1) = 0 \) để tìm giá trị lớn nhất và nhỏ nhất.
Giá trị nhỏ nhất là \( 0 \) và giá trị lớn nhất là \( 2 \).
- Bài tập 10: Tính tích phân hàm mũ
Tính tích phân sau: \( \int_1^2 e^{2x} \, dx \)
Lời giải:
Sử dụng công thức tích phân cơ bản:
\[ \int e^{2x} \, dx = \frac{1}{2}e^{2x} + C \]Áp dụng giới hạn từ \( 1 \) đến \( 2 \):
\[ \int_1^2 e^{2x} \, dx = \frac{1}{2}e^{4} - \frac{1}{2}e^{2} \]
XEM THÊM:
Bài tập về cấu trúc ngữ pháp Tiếng Anh
Dưới đây là các bài tập về cấu trúc ngữ pháp tiếng Anh nhằm giúp bạn củng cố và nắm vững các kiến thức đã học. Các bài tập bao gồm nhiều dạng khác nhau từ cơ bản đến nâng cao, giúp bạn hiểu rõ hơn về cách sử dụng các cấu trúc ngữ pháp trong tiếng Anh.
Bài tập 1: Chọn đáp án đúng
Chọn đáp án đúng cho mỗi câu dưới đây:
-
Câu nào đúng?
- A. She don't like ice cream.
- B. She doesn't likes ice cream.
- C. She doesn't like ice cream.
- D. She don't likes ice cream.
-
Câu nào đúng?
- A. They has gone to the market.
- B. They have gone to the market.
- C. They have went to the market.
- D. They has went to the market.
Bài tập 2: Hoàn thành câu
Hoàn thành các câu dưới đây bằng cách điền từ phù hợp:
- He ________ (play) football every Sunday.
- We ________ (not/see) her since last year.
- They ________ (study) English for two hours every day.
Bài tập 3: Sắp xếp từ thành câu hoàn chỉnh
Sắp xếp các từ dưới đây để tạo thành câu hoàn chỉnh:
-
always / she / to / early / school / goes
Trả lời: She always goes to school early.
-
have / they / homework / their / finished / already
Trả lời: They have already finished their homework.
Bài tập 4: Chia động từ trong ngoặc
Chia các động từ trong ngoặc để hoàn thành câu:
- She ________ (not/go) to the party last night.
- We ________ (visit) our grandparents next weekend.
- He ________ (work) at this company for five years.
Bài tập 5: Chọn cấu trúc câu đúng
Chọn câu có cấu trúc đúng:
-
Câu nào đúng?
- A. I have never see him before.
- B. I has never seen him before.
- C. I have never seen him before.
- D. I had never see him before.
-
Câu nào đúng?
- A. She is going to meets her friends.
- B. She is going to meet her friends.
- C. She going to meet her friends.
- D. She is going meet her friends.
Bài tập 6: Phát hiện lỗi sai
Tìm và sửa lỗi sai trong các câu sau:
-
I doesn't like swimming.
Trả lời: I don't like swimming.
-
They was happy to see us.
Trả lời: They were happy to see us.
Hy vọng các bài tập trên sẽ giúp bạn nắm vững hơn về cấu trúc ngữ pháp tiếng Anh. Chúc bạn học tốt!
Bài tập về động lực học
Bài tập về động lực học giúp bạn hiểu rõ hơn về các khái niệm cơ bản như lực, gia tốc, khối lượng, và cách chúng tác động lên vật thể. Dưới đây là một số bài tập điển hình để bạn luyện tập:
Bài tập 1: Định luật II Newton
Một vật có khối lượng \( m = 5 \, \text{kg} \) chịu tác dụng của một lực không đổi \( F = 20 \, \text{N} \) theo phương ngang. Hãy tính gia tốc của vật và quãng đường vật đi được sau 4 giây nếu vật bắt đầu chuyển động từ trạng thái nghỉ.
- Giải: Áp dụng định luật II Newton, ta có:
- \[ a = \frac{F}{m} = \frac{20 \, \text{N}}{5 \, \text{kg}} = 4 \, \text{m/s}^2 \]
- Quãng đường vật đi được sau 4 giây:
- \[ S = \frac{1}{2} a t^2 = \frac{1}{2} \times 4 \, \text{m/s}^2 \times (4 \, \text{s})^2 = 32 \, \text{m} \]
Bài tập 2: Động lượng và định luật bảo toàn động lượng
Một viên đạn có khối lượng \( m_1 = 0.02 \, \text{kg} \) đang bay với vận tốc \( v_1 = 300 \, \text{m/s} \) và va chạm đàn hồi vào một vật khác có khối lượng \( m_2 = 3 \, \text{kg} \) đang đứng yên. Tính vận tốc của hai vật sau va chạm.
- Giải: Sử dụng định luật bảo toàn động lượng và bảo toàn động năng, ta có:
- \[ m_1 v_1 + m_2 v_2 = m_1 v'_1 + m_2 v'_2 \]
- Giải hệ phương trình để tìm \( v'_1 \) và \( v'_2 \).
Bài tập 3: Công và năng lượng
Một vật có khối lượng \( m = 10 \, \text{kg} \) được kéo lên một mặt phẳng nghiêng không ma sát với chiều dài \( l = 5 \, \text{m} \) và góc nghiêng \( \theta = 30^\circ \). Tính công cần thiết để kéo vật lên đỉnh của mặt phẳng nghiêng.
- Giải: Công thực hiện được tính bằng:
- \[ W = F \times d = m \times g \times h \]
- Với \( h = l \times \sin(\theta) = 5 \times \sin(30^\circ) = 2.5 \, \text{m} \), ta có:
- \[ W = 10 \times 9.8 \times 2.5 = 245 \, \text{J} \]
Các bài tập này cung cấp cơ hội tốt để bạn áp dụng lý thuyết vào thực hành, giúp củng cố kiến thức về động lực học và chuẩn bị cho các kỳ thi quan trọng.

Bài tập Tiếng Anh giao tiếp
Bài tập Tiếng Anh giao tiếp giúp người học rèn luyện khả năng nghe, nói và phản xạ ngôn ngữ trong các tình huống thực tế. Dưới đây là một số bài tập cơ bản để cải thiện kỹ năng giao tiếp Tiếng Anh:
Bài tập 1: Luyện nghe và trả lời câu hỏi
Nghe đoạn hội thoại ngắn sau đó trả lời câu hỏi liên quan:
- Nghe đoạn hội thoại:
- Câu hỏi: Người nói thứ hai cần gì?
- Trả lời: Người nói thứ hai cần thông tin về dự án mới.
Đoạn hội thoại: "Hello! How can I help you today?" - "Hi, I need some information about the new project."
Bài tập 2: Thực hành đối thoại
Hãy đóng vai trong tình huống sau và viết đoạn đối thoại:
- Tình huống: Bạn là nhân viên khách sạn, một khách hàng muốn đặt phòng.
- Gợi ý: Bắt đầu bằng việc chào hỏi và hỏi thông tin về loại phòng, ngày đặt, và dịch vụ đi kèm.
- Ví dụ:
| Khách: | "Hi, I'd like to book a room for two nights." |
| Nhân viên: | "Certainly! May I have your check-in and check-out dates?" |
Bài tập 3: Luyện phản xạ với câu hỏi Yes/No
Nghe và phản xạ nhanh với câu hỏi Yes/No:
- Câu hỏi: "Do you like coffee?"
- Phản xạ: "Yes, I do." hoặc "No, I don't."
Bài tập 4: Luyện phát âm
Thực hành phát âm đúng các từ khó và câu dài:
- Từ vựng: Architect, comfortable, schedule
- Câu luyện phát âm: "She sells sea shells by the seashore."
Bài tập giao tiếp Tiếng Anh cần được luyện tập đều đặn hàng ngày để nâng cao sự tự tin và khả năng sử dụng ngôn ngữ trong các tình huống giao tiếp thực tế.
Bài tập về giải tích cơ bản
Trong phần này, chúng ta sẽ làm quen với các bài tập cơ bản về giải tích, bao gồm các khái niệm như giới hạn, đạo hàm, tích phân và chuỗi. Các bài tập sẽ giúp bạn nắm vững lý thuyết và ứng dụng của giải tích trong toán học.
1. Bài tập về giới hạn
- Tính giới hạn sau: \[ \lim_{{x \to 0}} \frac{{\sin x}}{{x}} \]
- Tìm giới hạn của dãy số: \[ a_n = \frac{n}{{n+1}} \] khi \(n\) tiến tới vô cùng.
2. Bài tập về đạo hàm
- Tính đạo hàm của hàm số: \[ f(x) = x^3 - 3x^2 + 2x - 5 \]
- Tìm giá trị lớn nhất và nhỏ nhất của hàm số: \[ g(x) = \frac{{2x}}{{x^2 + 1}} \]
3. Bài tập về tích phân
- Tính tích phân bất định: \[ \int (2x^2 + 3x + 1) \, dx \]
- Tính tích phân xác định: \[ \int_{{0}}^{{1}} \frac{{1}}{{1 + x^2}} \, dx \]
4. Bài tập về chuỗi
- Kiểm tra tính hội tụ của chuỗi: \[ \sum_{{n=1}}^{\infty} \frac{1}{{n^2}} \]
- Tính tổng của chuỗi hình học: \[ S = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots \]
Những bài tập trên giúp bạn củng cố kiến thức về giải tích cơ bản và rèn luyện kỹ năng giải quyết các bài toán trong lĩnh vực này.

Bài tập về cơ học chất lỏng
Cơ học chất lỏng là một nhánh của cơ học nghiên cứu về hành vi của chất lỏng (chất lỏng và khí) khi chúng chịu tác động của các lực. Dưới đây là các bài tập cơ bản nhằm giúp bạn nắm vững các khái niệm quan trọng trong cơ học chất lỏng, từ định luật Bernoulli đến phương trình liên tục và phương trình Navier-Stokes.
1. Bài tập về áp suất trong chất lỏng
- Một bình chứa nước có độ sâu \(h = 10 \, \text{m}\). Tính áp suất tại đáy bình: \[ P = \rho gh \] Biết rằng khối lượng riêng của nước là \(\rho = 1000 \, \text{kg/m}^3\) và gia tốc trọng trường là \(g = 9.81 \, \text{m/s}^2\).
2. Bài tập về định luật Bernoulli
- Một ống dẫn nước có đường kính thay đổi từ \(d_1 = 0.1 \, \text{m}\) ở đoạn đầu đến \(d_2 = 0.05 \, \text{m}\) ở đoạn cuối. Tính vận tốc của nước ở đoạn cuối \(v_2\) nếu vận tốc ở đoạn đầu \(v_1 = 2 \, \text{m/s}\), và áp dụng định luật Bernoulli: \[ P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2 \] Giả sử áp suất không thay đổi.
3. Bài tập về phương trình liên tục
- Một ống dẫn có lưu lượng dòng chảy không đổi. Tính vận tốc của dòng chảy ở đoạn ống hẹp hơn nếu biết vận tốc ở đoạn rộng hơn là \(v = 3 \, \text{m/s}\), và diện tích mặt cắt của đoạn rộng hơn là \(A_1 = 0.02 \, \text{m}^2\) và đoạn hẹp hơn là \(A_2 = 0.01 \, \text{m}^2\). Áp dụng phương trình liên tục: \[ A_1 v_1 = A_2 v_2 \]
4. Bài tập về lực đẩy Archimedes
- Một vật có thể tích \(V = 0.5 \, \text{m}^3\) được thả vào trong nước. Tính lực đẩy Archimedes tác dụng lên vật, biết rằng khối lượng riêng của nước là \(\rho = 1000 \, \text{kg/m}^3\): \[ F_A = \rho g V \]
Các bài tập trên giúp bạn hiểu rõ hơn về cơ học chất lỏng thông qua việc áp dụng lý thuyết vào các tình huống thực tế. Việc giải các bài tập này một cách chi tiết và cẩn thận sẽ giúp bạn nắm vững các nguyên lý cơ bản của ngành học này.
Bài tập về xác suất thống kê
Dưới đây là một số bài tập về xác suất thống kê giúp bạn rèn luyện kiến thức cơ bản và nâng cao trong môn học này. Các bài tập được trình bày theo mức độ khó tăng dần, giúp bạn từng bước làm quen và thành thạo các kỹ năng cần thiết.
Bài tập 1: Xác suất của một biến cố
Giả sử có một hộp chứa 3 quả bóng đỏ và 2 quả bóng xanh. Chọn ngẫu nhiên một quả bóng từ hộp. Tính xác suất để chọn được quả bóng đỏ.
- Lời giải: Gọi biến cố A là "chọn được quả bóng đỏ". Xác suất của biến cố A được tính bằng công thức: \[ P(A) = \frac{\text{số kết quả thuận lợi}}{\text{tổng số kết quả có thể xảy ra}} = \frac{3}{5} \]
Bài tập 2: Xác suất có điều kiện
Giả sử rằng trong một lớp học có 10 học sinh giỏi Toán và 5 học sinh giỏi Văn. Trong đó, có 3 học sinh giỏi cả Toán lẫn Văn. Chọn ngẫu nhiên một học sinh, biết rằng học sinh đó giỏi Toán, tính xác suất để học sinh đó cũng giỏi Văn.
- Lời giải: Gọi A là biến cố "học sinh giỏi Toán" và B là biến cố "học sinh giỏi Văn". Xác suất có điều kiện của B khi biết A được tính theo công thức: \[ P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{\frac{3}{15}}{\frac{10}{15}} = \frac{3}{10} \]
Bài tập 3: Quy luật phân phối xác suất
Cho một biến ngẫu nhiên X có phân phối chuẩn với kỳ vọng \(\mu = 0\) và độ lệch chuẩn \(\sigma = 1\). Tính xác suất để X nằm trong khoảng từ -1 đến 1.
- Lời giải: Xác suất để biến ngẫu nhiên X nằm trong khoảng từ -1 đến 1 được tính bằng cách sử dụng bảng phân phối chuẩn hoặc phần mềm hỗ trợ: \[ P(-1 \leq X \leq 1) \approx 0.6826 \]
Bài tập 4: Luật số lớn
Giả sử rằng một đồng xu không đối xứng có xác suất xuất hiện mặt ngửa là 0.6. Gieo đồng xu 100 lần, hãy ước tính xác suất để số lần xuất hiện mặt ngửa nằm trong khoảng từ 55 đến 65.
- Lời giải: Sử dụng định lý luật số lớn và định lý giới hạn trung tâm để ước tính xác suất này. Gọi X là số lần xuất hiện mặt ngửa trong 100 lần gieo, khi đó: \[ X \sim N(60, 4) \] Sử dụng bảng phân phối chuẩn, tính xác suất cho khoảng từ 55 đến 65.
Trên đây là một số bài tập giúp bạn rèn luyện các kỹ năng xác suất thống kê. Để nắm vững kiến thức, hãy cố gắng tự mình giải các bài tập trước khi xem lời giải.