Chủ đề đường tròn lượng giác: Đường tròn lượng giác là một công cụ quan trọng trong toán học, giúp xác định các giá trị sin, cos, tan của các góc đặc biệt. Bài viết này sẽ giúp bạn khám phá các khái niệm cơ bản, ứng dụng trong giải toán và thực tiễn của đường tròn lượng giác, cùng với các bài tập để củng cố kiến thức.
Mục lục
- Khái Niệm Đường Tròn Lượng Giác
- Góc và Giá Trị Lượng Giác
- Chia Phần Tư Trên Đường Tròn Lượng Giác
- Công Thức Xác Định Giá Trị Lượng Giác
- Ứng Dụng Của Đường Tròn Lượng Giác
- Bài Tập Thực Hành
- Góc và Giá Trị Lượng Giác
- Chia Phần Tư Trên Đường Tròn Lượng Giác
- Công Thức Xác Định Giá Trị Lượng Giác
- Ứng Dụng Của Đường Tròn Lượng Giác
- Bài Tập Thực Hành
- Chia Phần Tư Trên Đường Tròn Lượng Giác
- Công Thức Xác Định Giá Trị Lượng Giác
- Ứng Dụng Của Đường Tròn Lượng Giác
- Bài Tập Thực Hành
- Công Thức Xác Định Giá Trị Lượng Giác
- Ứng Dụng Của Đường Tròn Lượng Giác
- Bài Tập Thực Hành
- Ứng Dụng Của Đường Tròn Lượng Giác
- YOUTUBE: Khám phá cách sử dụng đường tròn lượng giác một cách hiệu quả trong các bài toán lượng giác. Video hướng dẫn chi tiết và dễ hiểu dành cho học sinh và người yêu toán học.
Khái Niệm Đường Tròn Lượng Giác
Đường tròn lượng giác là một công cụ quan trọng trong toán học, đặc biệt là trong hình học và lượng giác. Đường tròn này có tâm là gốc tọa độ O và bán kính bằng 1 đơn vị.

.png)
Góc và Giá Trị Lượng Giác
Một số góc đặc biệt và các giá trị lượng giác của chúng:
| Góc | Sin | Cos | Tan |
| 0° (\(0\)) | 0 | 1 | 0 |
| 30° (\(\frac{\pi}{6}\)) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (\(\frac{\pi}{4}\)) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (\(\frac{\pi}{3}\)) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (\(\frac{\pi}{2}\)) | 1 | 0 | Không xác định |
Chia Phần Tư Trên Đường Tròn Lượng Giác
Đường tròn lượng giác được chia thành bốn phần tư, mỗi phần tư có các dấu khác nhau cho giá trị của sin, cos và tan:
- Phần tư I (0° đến 90°): Sin dương, Cos dương, Tan dương.
- Phần tư II (90° đến 180°): Sin dương, Cos âm, Tan âm.
- Phần tư III (180° đến 270°): Sin âm, Cos âm, Tan dương.
- Phần tư IV (270° đến 360°): Sin âm, Cos dương, Tan âm.

Công Thức Xác Định Giá Trị Lượng Giác
Các công thức cơ bản để xác định giá trị lượng giác:
- Sin: Tỉ số giữa cạnh đối và cạnh huyền.
- Cos: Tỉ số giữa cạnh kề và cạnh huyền.
- Tan: Tỉ số giữa cạnh đối và cạnh kề.
XEM THÊM:
Ứng Dụng Của Đường Tròn Lượng Giác
Đường tròn lượng giác không chỉ giới hạn trong toán học mà còn được áp dụng rộng rãi trong vật lý, kỹ thuật và nhiều lĩnh vực khác. Một số ứng dụng cụ thể:
- Trong toán học: Giải phương trình lượng giác, xác định giá trị sin, cos, tan cho các góc.
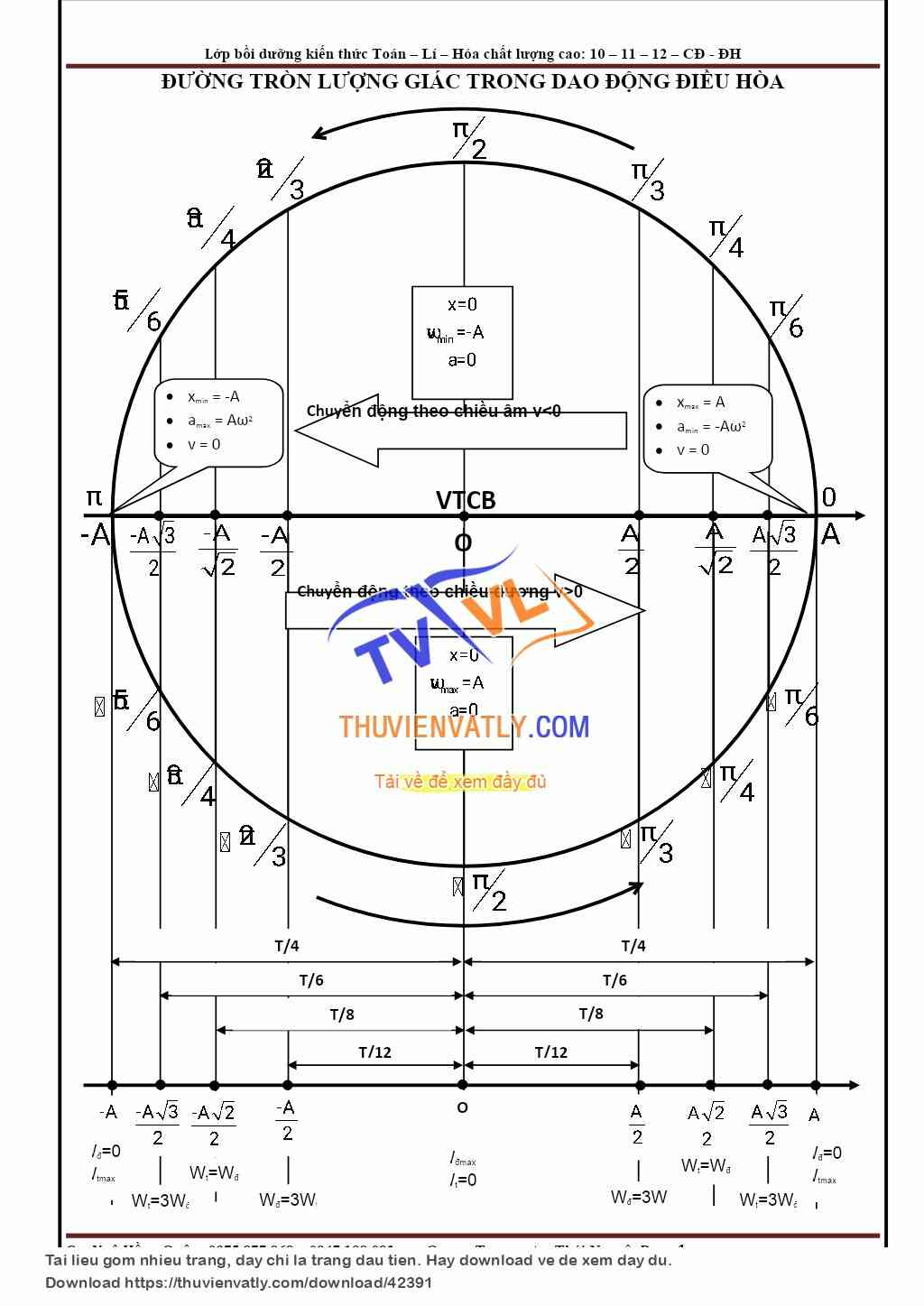
- Trong vật lý: Phân tích chuyển động tròn đều, dao động điều hòa và sóng.

Bài Tập Thực Hành
Một số bài tập cơ bản về đường tròn lượng giác:
- Xác định các điểm trên đường tròn lượng giác với các góc cho trước.
- Tính giá trị lượng giác của các góc đặc biệt.
- Phân tích dấu của sin, cos và tan trong các phần tư khác nhau.
Góc và Giá Trị Lượng Giác
Một số góc đặc biệt và các giá trị lượng giác của chúng:
| Góc | Sin | Cos | Tan |
| 0° (\(0\)) | 0 | 1 | 0 |
| 30° (\(\frac{\pi}{6}\)) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 45° (\(\frac{\pi}{4}\)) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° (\(\frac{\pi}{3}\)) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
| 90° (\(\frac{\pi}{2}\)) | 1 | 0 | Không xác định |
Chia Phần Tư Trên Đường Tròn Lượng Giác
Đường tròn lượng giác được chia thành bốn phần tư, mỗi phần tư có các dấu khác nhau cho giá trị của sin, cos và tan:
- Phần tư I (0° đến 90°): Sin dương, Cos dương, Tan dương.
- Phần tư II (90° đến 180°): Sin dương, Cos âm, Tan âm.
- Phần tư III (180° đến 270°): Sin âm, Cos âm, Tan dương.
- Phần tư IV (270° đến 360°): Sin âm, Cos dương, Tan âm.

Công Thức Xác Định Giá Trị Lượng Giác
Các công thức cơ bản để xác định giá trị lượng giác:
- Sin: Tỉ số giữa cạnh đối và cạnh huyền.
- Cos: Tỉ số giữa cạnh kề và cạnh huyền.
- Tan: Tỉ số giữa cạnh đối và cạnh kề.
Ứng Dụng Của Đường Tròn Lượng Giác
Đường tròn lượng giác không chỉ giới hạn trong toán học mà còn được áp dụng rộng rãi trong vật lý, kỹ thuật và nhiều lĩnh vực khác. Một số ứng dụng cụ thể:
- Trong toán học: Giải phương trình lượng giác, xác định giá trị sin, cos, tan cho các góc.
- Trong vật lý: Phân tích chuyển động tròn đều, dao động điều hòa và sóng.

Bài Tập Thực Hành
Một số bài tập cơ bản về đường tròn lượng giác:
- Xác định các điểm trên đường tròn lượng giác với các góc cho trước.
- Tính giá trị lượng giác của các góc đặc biệt.
- Phân tích dấu của sin, cos và tan trong các phần tư khác nhau.
Chia Phần Tư Trên Đường Tròn Lượng Giác
Đường tròn lượng giác được chia thành bốn phần tư, mỗi phần tư có các dấu khác nhau cho giá trị của sin, cos và tan:
- Phần tư I (0° đến 90°): Sin dương, Cos dương, Tan dương.
- Phần tư II (90° đến 180°): Sin dương, Cos âm, Tan âm.
- Phần tư III (180° đến 270°): Sin âm, Cos âm, Tan dương.
- Phần tư IV (270° đến 360°): Sin âm, Cos dương, Tan âm.
Công Thức Xác Định Giá Trị Lượng Giác
Các công thức cơ bản để xác định giá trị lượng giác:
- Sin: Tỉ số giữa cạnh đối và cạnh huyền.
- Cos: Tỉ số giữa cạnh kề và cạnh huyền.
- Tan: Tỉ số giữa cạnh đối và cạnh kề.

Ứng Dụng Của Đường Tròn Lượng Giác
Đường tròn lượng giác không chỉ giới hạn trong toán học mà còn được áp dụng rộng rãi trong vật lý, kỹ thuật và nhiều lĩnh vực khác. Một số ứng dụng cụ thể:
- Trong toán học: Giải phương trình lượng giác, xác định giá trị sin, cos, tan cho các góc.
- Trong vật lý: Phân tích chuyển động tròn đều, dao động điều hòa và sóng.
Bài Tập Thực Hành
Một số bài tập cơ bản về đường tròn lượng giác:
- Xác định các điểm trên đường tròn lượng giác với các góc cho trước.
- Tính giá trị lượng giác của các góc đặc biệt.
- Phân tích dấu của sin, cos và tan trong các phần tư khác nhau.
Công Thức Xác Định Giá Trị Lượng Giác
Các công thức cơ bản để xác định giá trị lượng giác:
- Sin: Tỉ số giữa cạnh đối và cạnh huyền.
- Cos: Tỉ số giữa cạnh kề và cạnh huyền.
- Tan: Tỉ số giữa cạnh đối và cạnh kề.

Ứng Dụng Của Đường Tròn Lượng Giác
Đường tròn lượng giác không chỉ giới hạn trong toán học mà còn được áp dụng rộng rãi trong vật lý, kỹ thuật và nhiều lĩnh vực khác. Một số ứng dụng cụ thể:
- Trong toán học: Giải phương trình lượng giác, xác định giá trị sin, cos, tan cho các góc.
- Trong vật lý: Phân tích chuyển động tròn đều, dao động điều hòa và sóng.
Bài Tập Thực Hành
Một số bài tập cơ bản về đường tròn lượng giác:
- Xác định các điểm trên đường tròn lượng giác với các góc cho trước.
- Tính giá trị lượng giác của các góc đặc biệt.
- Phân tích dấu của sin, cos và tan trong các phần tư khác nhau.
Ứng Dụng Của Đường Tròn Lượng Giác
Đường tròn lượng giác không chỉ giới hạn trong toán học mà còn được áp dụng rộng rãi trong vật lý, kỹ thuật và nhiều lĩnh vực khác. Một số ứng dụng cụ thể:
- Trong toán học: Giải phương trình lượng giác, xác định giá trị sin, cos, tan cho các góc.
- Trong vật lý: Phân tích chuyển động tròn đều, dao động điều hòa và sóng.






















