Chủ đề bảng xếp hạng bóng đá giải pháp: Bảng xếp hạng bóng đá giải pháp là một công cụ quan trọng để theo dõi và đánh giá hiệu suất của các đội bóng hàng đầu. Bài viết này sẽ cung cấp thông tin cập nhật mới nhất về bảng xếp hạng, cùng với các phân tích chi tiết về phong độ, chiến thuật và những yếu tố ảnh hưởng đến thứ hạng của các đội. Hãy cùng khám phá những thông tin hữu ích này để có cái nhìn tổng quan và chính xác về giải đấu.
Mục lục
- Bảng Xếp Hạng Bóng Đá Giải Pháp
- Mục Lục Tổng Hợp
- Bài Tập Thực Hành (Nếu Áp Dụng Cho Toán, Lý, Hoặc Tiếng Anh)
- Dạng Bài Tập 1: Giải Phương Trình
- Dạng Bài Tập 2: Phân Tích Dữ Liệu
- Dạng Bài Tập 3: Tính Toán Tỉ Lệ
- Dạng Bài Tập 4: Giải Bất Phương Trình
- Dạng Bài Tập 5: Đọc Hiểu Văn Bản Tiếng Anh
- Dạng Bài Tập 6: Viết Đoạn Văn Ngắn Bằng Tiếng Anh
- Dạng Bài Tập 7: Tính Toán Lượng Giác
- Dạng Bài Tập 8: Giải Toán Đố
- Dạng Bài Tập 9: Thực Hành Phân Tích Cấu Trúc Câu Tiếng Anh
- Dạng Bài Tập 10: Tìm Giới Hạn Của Dãy Số
Bảng Xếp Hạng Bóng Đá Giải Pháp
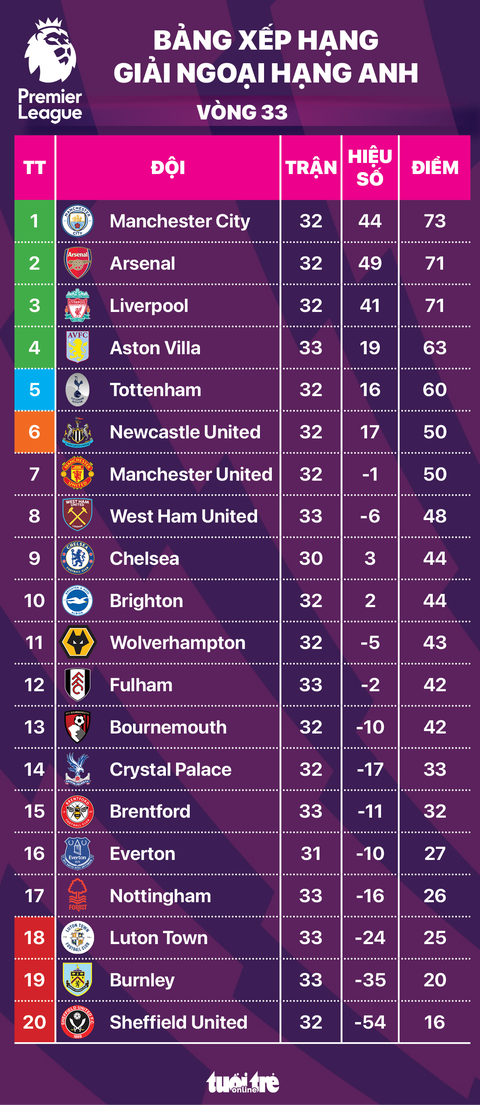
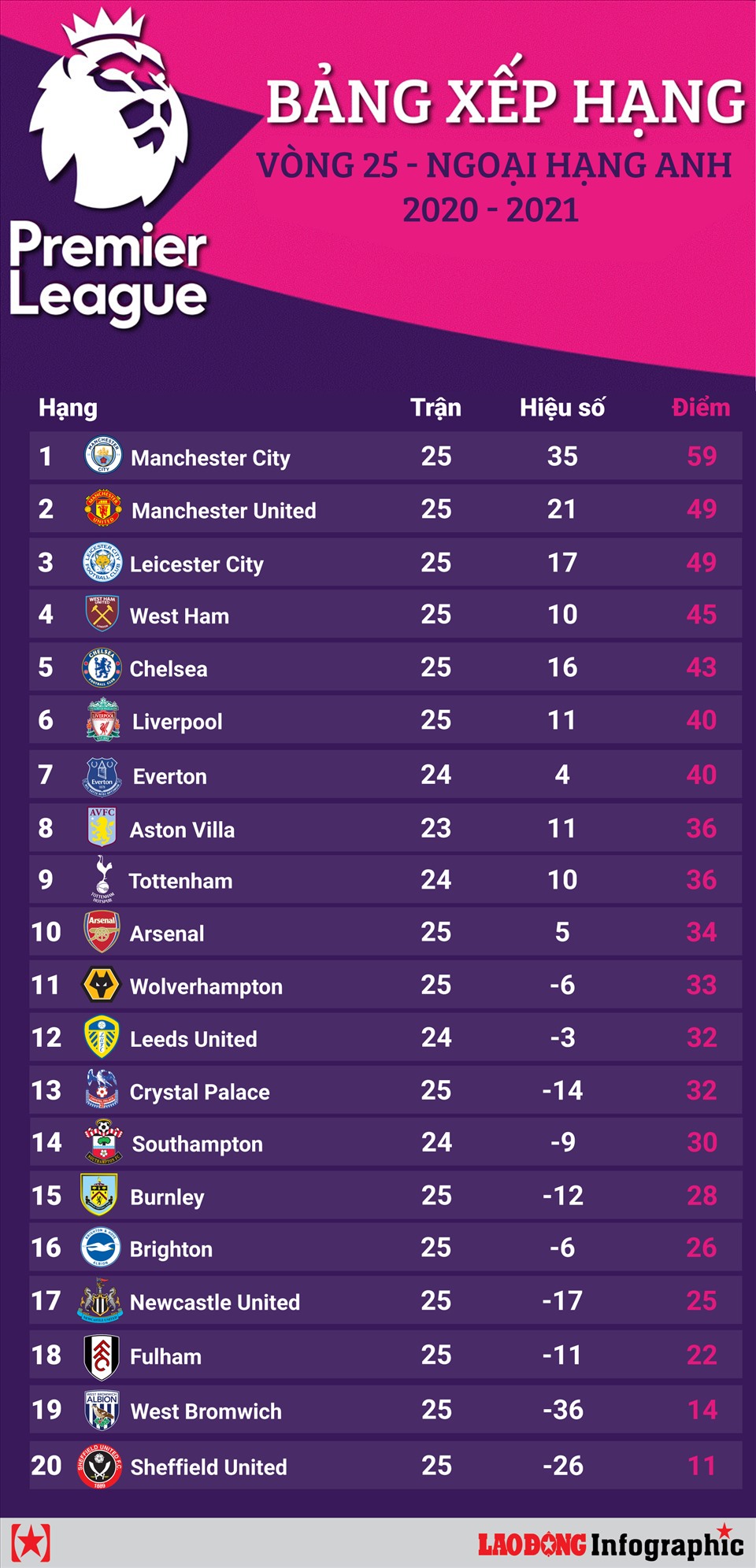
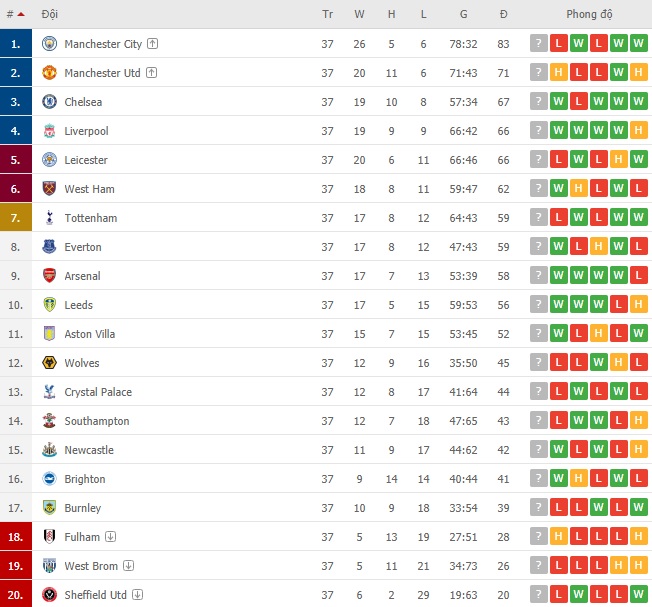
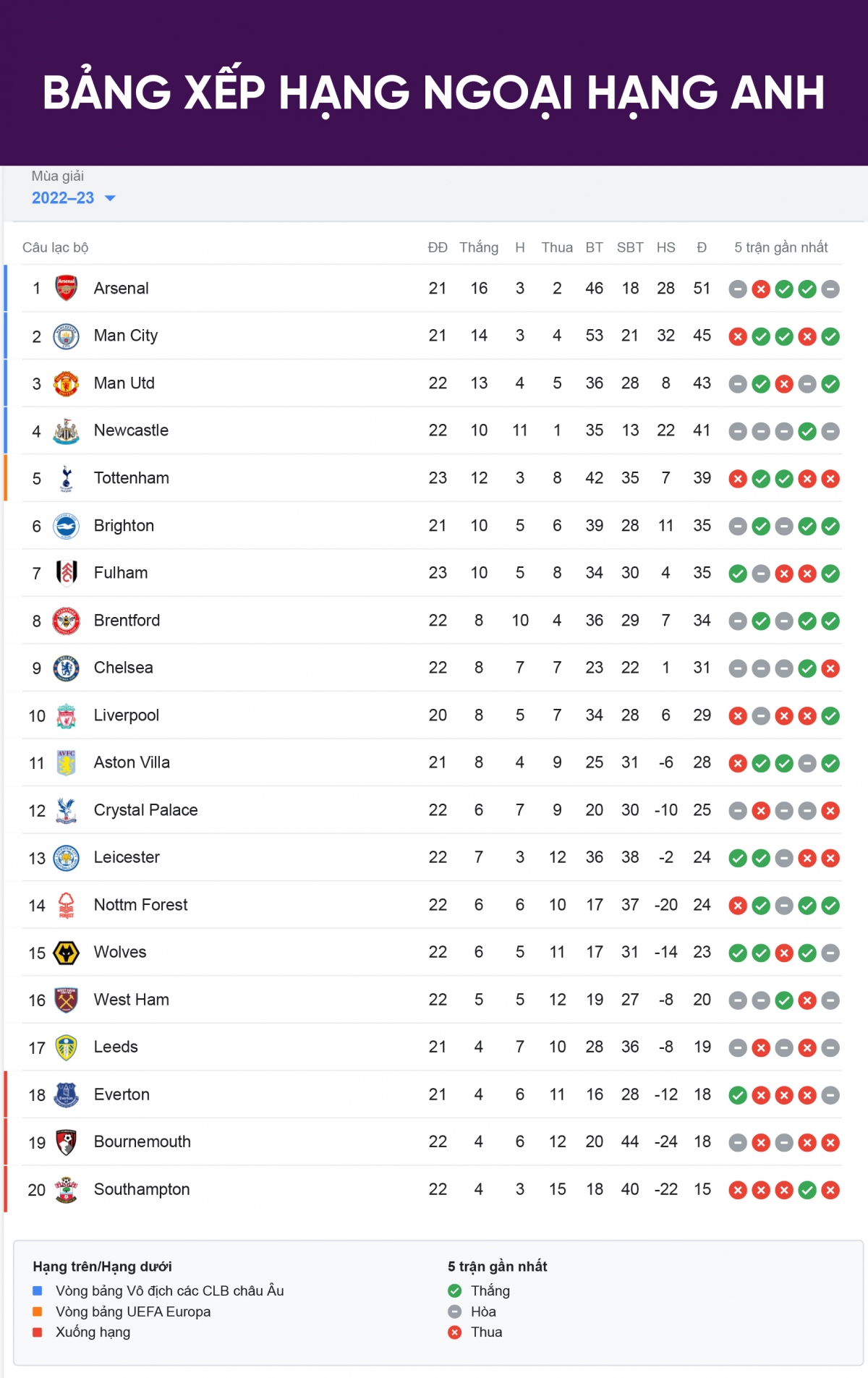
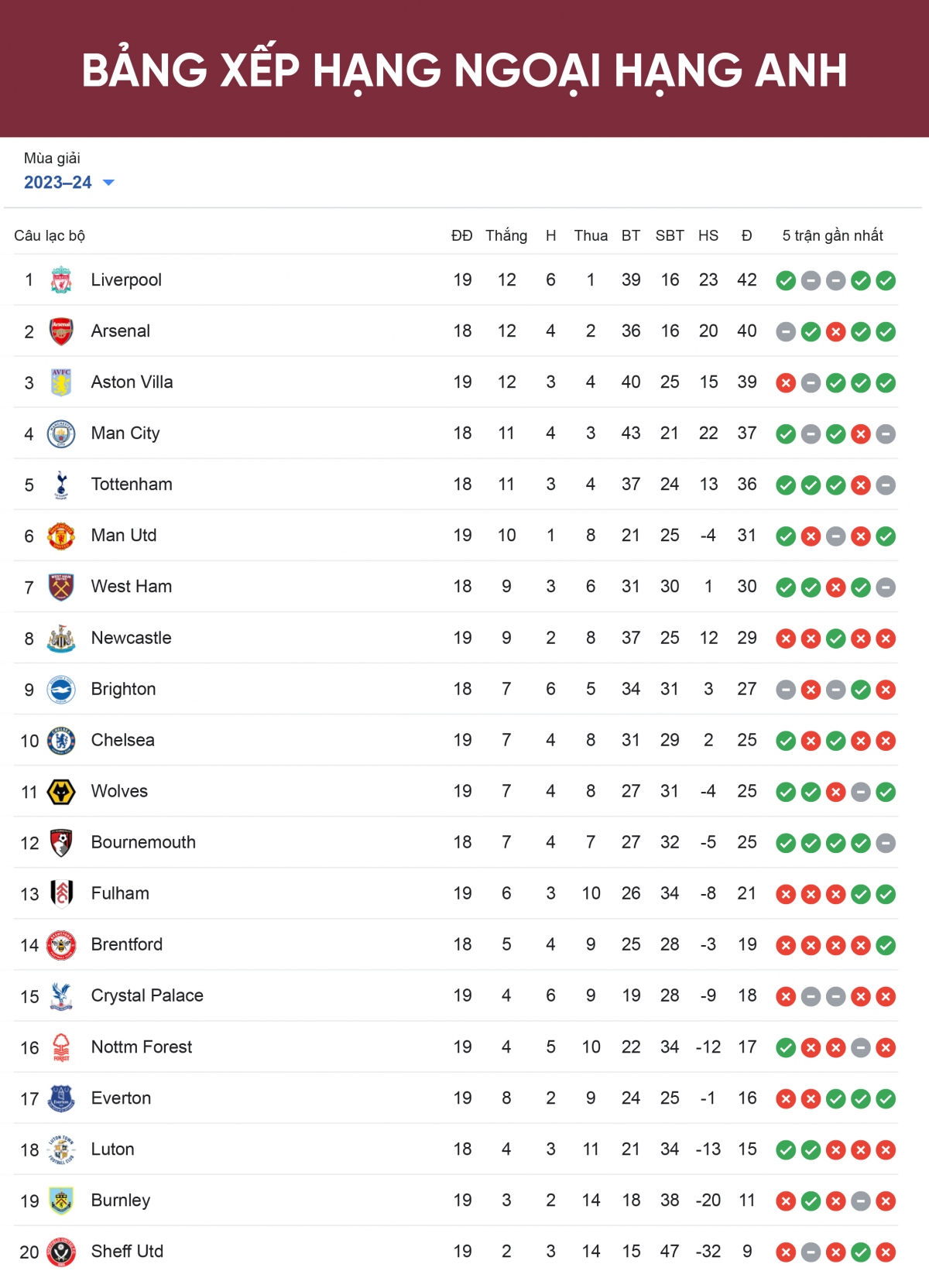
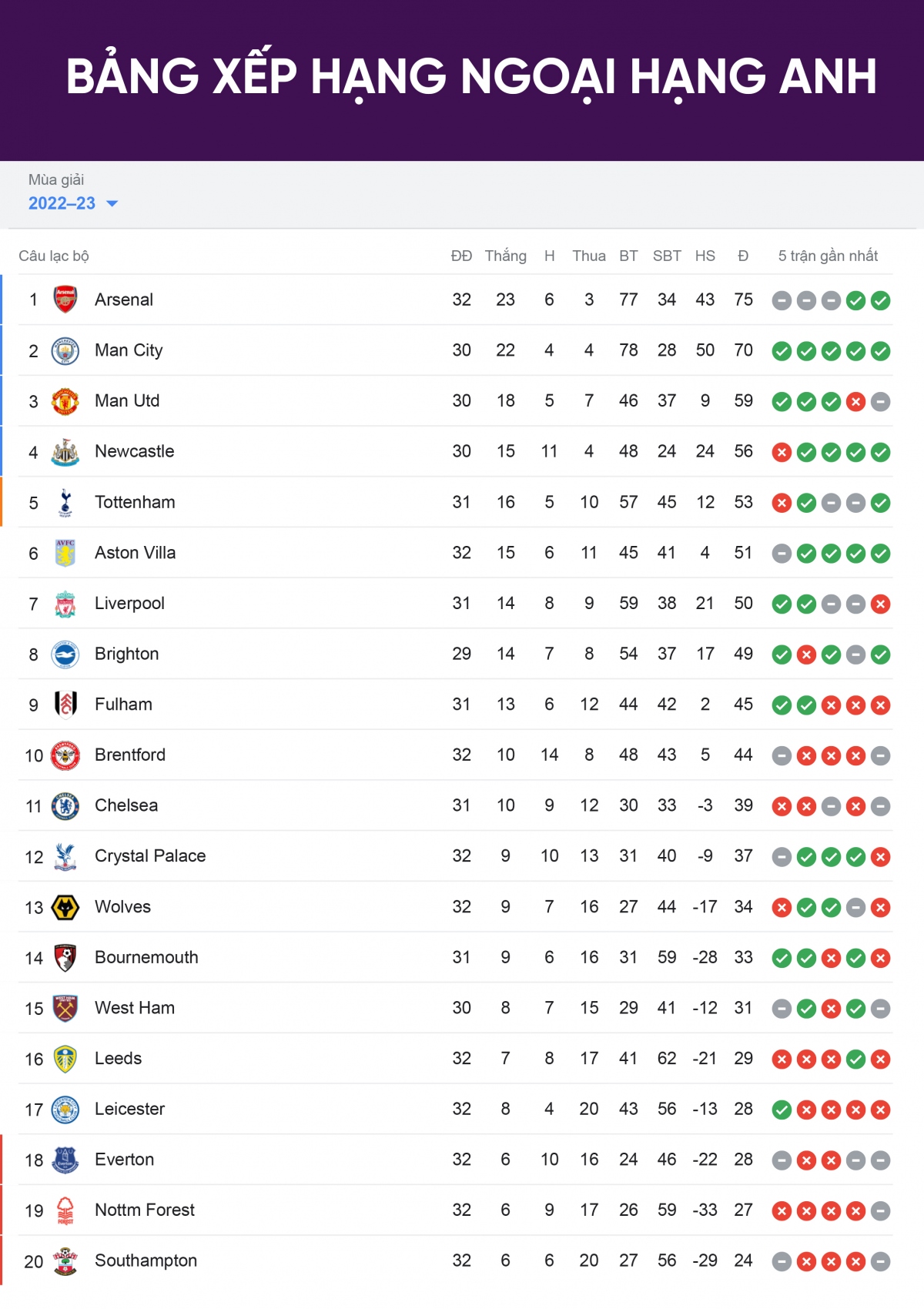
Bảng xếp hạng bóng đá giải Pháp là nơi tổng hợp kết quả và thứ hạng của các đội bóng tham gia các giải đấu hàng đầu như Ligue 1, Ligue 2, và các giải đấu cúp quốc gia. Thông tin về bảng xếp hạng này rất quan trọng cho người hâm mộ và các chuyên gia phân tích để theo dõi sự thay đổi thứ hạng của các đội bóng qua từng vòng đấu.
Bảng Xếp Hạng Ligue 1
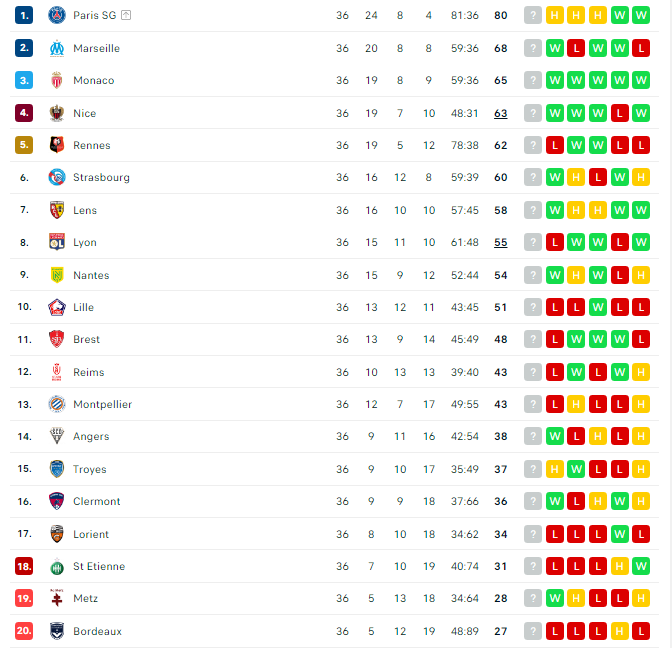
Ligue 1 là giải đấu hàng đầu của bóng đá Pháp, nơi quy tụ những câu lạc bộ mạnh nhất trong nước. Bảng xếp hạng Ligue 1 cung cấp thông tin về số trận thắng, thua, hòa, điểm số, và hiệu số bàn thắng bại của các đội.
- Vị trí số 1: Đội bóng dẫn đầu bảng xếp hạng, thường là ứng viên vô địch.
- Vị trí giữa bảng: Những đội bóng có mục tiêu tham gia các giải đấu châu Âu.
- Vị trí cuối bảng: Các đội có nguy cơ rớt hạng.
Bảng Xếp Hạng Ligue 2
Ligue 2 là giải đấu hạng dưới của Ligue 1, nhưng vẫn có sức cạnh tranh mạnh mẽ. Các đội bóng hàng đầu tại Ligue 2 có cơ hội thăng hạng lên chơi tại Ligue 1 vào mùa giải tiếp theo.
- Vị trí số 1: Đội bóng có thành tích tốt nhất, chắc chắn thăng hạng.
- Vị trí giữa bảng: Các đội an toàn và có thể cạnh tranh vé thăng hạng qua vòng play-off.
- Vị trí cuối bảng: Những đội phải đấu tranh để tránh xuống hạng 3.
Bảng Xếp Hạng Cúp Quốc Gia Pháp
Cúp quốc gia là một giải đấu loại trực tiếp, nơi các đội bóng từ mọi cấp độ của bóng đá Pháp có cơ hội tranh tài. Bảng xếp hạng cúp quốc gia thường chỉ ra các đội đã tiến xa nhất trong giải đấu.
- Các vòng đầu tiên: Những đội từ các giải hạng dưới thường gây bất ngờ.
- Các vòng sau: Những đội mạnh và có nhiều kinh nghiệm thường chiếm ưu thế.
- Chung kết: Hai đội mạnh nhất đối đầu để giành chiếc cúp danh giá.
Ý Nghĩa Của Bảng Xếp Hạng
Bảng xếp hạng không chỉ là kết quả mà còn phản ánh phong độ và chiến lược của các đội bóng. Người hâm mộ có thể dựa vào đó để đánh giá sức mạnh của đội bóng mình yêu thích, trong khi các nhà phân tích có thể sử dụng thông tin để đưa ra các dự đoán cho các trận đấu sắp tới.
Kết Luận
Bảng xếp hạng bóng đá giải Pháp là một phần quan trọng trong việc theo dõi và đánh giá bóng đá chuyên nghiệp. Nó không chỉ cung cấp thông tin về thứ hạng mà còn giúp người hâm mộ và các chuyên gia hiểu rõ hơn về sức mạnh và tiềm năng của các đội bóng.
.png)
Mục Lục Tổng Hợp
1. Giới Thiệu Chung Về Bảng Xếp Hạng Bóng Đá Giải Pháp
2. Phân Tích Chi Tiết Bảng Xếp Hạng Ligue 1
2.1. Top 5 Đội Dẫn Đầu
2.2. Những Đội Có Nguy Cơ Xuống Hạng
2.3. Thành Tích Nổi Bật Của Các Câu Lạc Bộ
3. Bảng Xếp Hạng Ligue 2 và Cơ Hội Thăng Hạng
4. Các Yếu Tố Ảnh Hưởng Đến Vị Trí Xếp Hạng
5. So Sánh Giữa Bảng Xếp Hạng Ligue 1 Và Các Giải Đấu Khác
6. Chiến Thuật và Phong Độ Của Các Đội Bóng Hàng Đầu
7. Dự Đoán Kết Quả Chung Cuộc
8. Tầm Quan Trọng Của Bảng Xếp Hạng Trong Mùa Giải
9. Ảnh Hưởng Của Bảng Xếp Hạng Đến Thị Trường Chuyển Nhượng
10. Nhận Định Từ Các Chuyên Gia Bóng Đá
Bài Tập Thực Hành (Nếu Áp Dụng Cho Toán, Lý, Hoặc Tiếng Anh)
Dạng Bài Tập 1: Giải Phương Trình
Cho phương trình bậc hai \[ax^2 + bx + c = 0\]. Tính nghiệm của phương trình khi \(a = 2\), \(b = -4\), và \(c = -6\).
Lời giải: Áp dụng công thức giải phương trình bậc hai \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\], tính toán để tìm nghiệm.
Dạng Bài Tập 2: Phân Tích Dữ Liệu
Thu thập dữ liệu từ bảng xếp hạng bóng đá và phân tích tỉ lệ chiến thắng của các đội đứng đầu. Dùng bảng dưới đây để tổ chức dữ liệu:
| Đội Bóng | Số Trận Thắng | Số Trận Hòa | Số Trận Thua |
|---|---|---|---|
| Đội A | 15 | 5 | 3 |
| Đội B | 12 | 8 | 3 |
Dạng Bài Tập 3: Tính Toán Tỉ Lệ
Giả sử đội bóng A đã chơi 23 trận, hãy tính tỉ lệ thắng của đội bóng này và biểu diễn dưới dạng phần trăm.
Lời giải: Tỉ lệ thắng = \(\frac{\text{Số trận thắng}}{\text{Tổng số trận}}\) x 100%. Tính toán để tìm tỉ lệ.
Dạng Bài Tập 4: Giải Bất Phương Trình
Giải bất phương trình \[3x + 5 > 2x + 9\] và biểu diễn tập nghiệm trên trục số.
Lời giải: Trừ \(2x\) từ cả hai vế, sau đó giải để tìm giá trị của \(x\).
Dạng Bài Tập 5: Đọc Hiểu Văn Bản Tiếng Anh
Đọc đoạn văn tiếng Anh sau và trả lời câu hỏi: "The team that leads the standings is often characterized by consistent performance and strong defense. How do these attributes contribute to their success?"
- What is meant by "consistent performance"?
- How does "strong defense" influence the results?
Dạng Bài Tập 6: Viết Đoạn Văn Ngắn Bằng Tiếng Anh
Viết một đoạn văn ngắn (khoảng 100 từ) bằng tiếng Anh về tầm quan trọng của chiến thuật trong các trận đấu bóng đá.
Dạng Bài Tập 7: Tính Toán Lượng Giác
Cho tam giác ABC vuông tại A. Biết \(AB = 3\), \(AC = 4\). Tính sin, cos và tan của góc B.
Lời giải: Áp dụng định lý Pythagore để tìm BC, sau đó tính các giá trị sin, cos và tan.
Dạng Bài Tập 8: Giải Toán Đố
Đội bóng X ghi được 20 bàn trong 5 trận gần nhất, trong đó có 3 trận ghi được nhiều hơn 3 bàn. Hỏi số bàn thắng trung bình của đội bóng này là bao nhiêu?
Lời giải: Tổng số bàn thắng chia cho số trận để tìm trung bình.
Dạng Bài Tập 9: Thực Hành Phân Tích Cấu Trúc Câu Tiếng Anh
Phân tích cấu trúc ngữ pháp của câu: "The team has been performing exceptionally well this season, leading the standings with a significant point margin."
Dạng Bài Tập 10: Tìm Giới Hạn Của Dãy Số
Tìm giới hạn của dãy số \(\lim_{{n \to \infty}} \frac{1}{n}\).
Lời giải: Áp dụng quy tắc cơ bản về giới hạn của dãy số.

Dạng Bài Tập 1: Giải Phương Trình
Dạng bài tập này yêu cầu giải các phương trình liên quan đến bảng xếp hạng bóng đá, trong đó các biến số và hệ số thường biểu diễn những điểm số, số trận thắng, số trận hòa và số trận thua của các đội bóng. Để giải các phương trình này, ta cần tuân theo các bước sau:
- Xác định các biến số đại diện cho các thông số trong bảng xếp hạng, ví dụ như:
- \(x\): Số trận thắng của đội bóng
- \(y\): Số trận hòa
- \(z\): Số trận thua
- Thiết lập phương trình dựa trên tổng số điểm của đội bóng, với mỗi trận thắng được tính 3 điểm, mỗi trận hòa được tính 1 điểm, và trận thua không có điểm: \[ \text{Tổng điểm} = 3x + y \]
- Giải phương trình để tìm các giá trị của \(x\), \(y\), và \(z\) phù hợp với các điều kiện thực tế, ví dụ như tổng số trận đã đấu và tổng số điểm: \[ 3x + y = \text{Tổng điểm} \] \[ x + y + z = \text{Tổng số trận} \]
- Kiểm tra lại các giá trị để đảm bảo tính hợp lý của chúng trong ngữ cảnh bảng xếp hạng bóng đá.
Một ví dụ cụ thể: Giả sử một đội bóng đã chơi 10 trận, giành được tổng cộng 17 điểm. Ta có thể thiết lập các phương trình:
\[
3x + y = 17
\]
\[
x + y + z = 10
\]
Giải hệ phương trình này để tìm \(x\), \(y\), và \(z\).
Sau khi tính toán, ta có thể đưa ra kết quả cụ thể cho số trận thắng, hòa, và thua của đội bóng đó, giúp hiểu rõ hơn về vị trí của họ trong bảng xếp hạng.
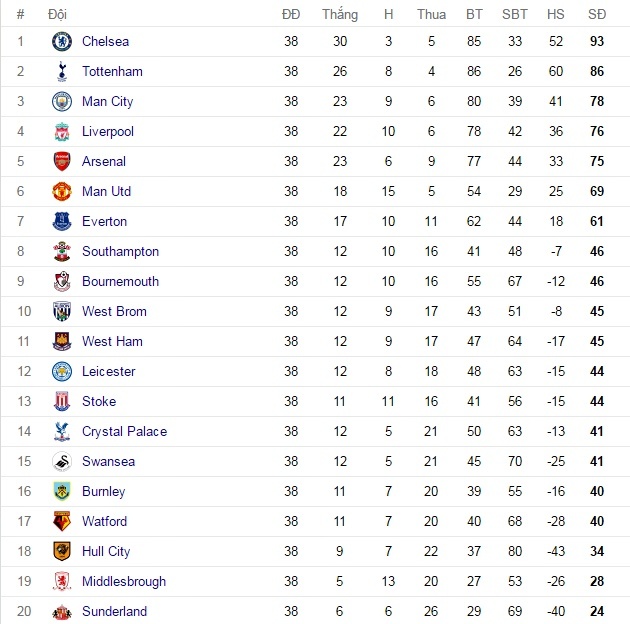
Dạng Bài Tập 2: Phân Tích Dữ Liệu
Trong dạng bài tập này, chúng ta sẽ thực hiện phân tích dữ liệu bảng xếp hạng bóng đá để rút ra các kết luận quan trọng về hiệu suất thi đấu của các đội bóng. Việc phân tích dữ liệu không chỉ giúp hiểu rõ hơn về phong độ của từng đội mà còn có thể dự đoán các xu hướng trong tương lai.
- Thu thập dữ liệu:
Đầu tiên, bạn cần thu thập dữ liệu từ bảng xếp hạng, bao gồm các chỉ số như số trận thắng, hòa, bại, hiệu số bàn thắng, và tổng điểm của mỗi đội. Ví dụ, bảng xếp hạng Ligue 1 của Pháp cho thấy Paris Saint-Germain dẫn đầu với số điểm cao nhất, tiếp theo là Marseille và Monaco.
- Phân tích hiệu suất:
Sử dụng dữ liệu thu thập được, bạn có thể tính toán các chỉ số hiệu suất như tỷ lệ thắng, hiệu suất ghi bàn và khả năng phòng ngự. Ví dụ, bạn có thể tính toán tỷ lệ thắng bằng công thức:
\[
\text{Tỷ lệ thắng} = \frac{\text{Số trận thắng}}{\text{Tổng số trận}}
\]Ví dụ: Với 38 trận đấu, nếu đội bóng thắng 26 trận, tỷ lệ thắng sẽ là:
\[
\frac{26}{38} \approx 0.684
\] - So sánh và đánh giá:
Sau khi tính toán các chỉ số, bạn có thể so sánh hiệu suất giữa các đội bóng để đánh giá phong độ tổng thể. Việc so sánh này có thể dựa trên điểm số hoặc các chỉ số phụ khác như hiệu số bàn thắng bại.
- Điểm số tổng thể: Đội nào có điểm số cao nhất thì đội đó có hiệu suất tốt nhất.
- Hiệu số bàn thắng: Đội có hiệu số bàn thắng tốt hơn thường có xu hướng tấn công mạnh và phòng ngự chắc chắn.
- Dự đoán xu hướng:
Dựa trên các phân tích trước đó, bạn có thể dự đoán xu hướng trong tương lai như đội nào có khả năng giữ vững phong độ hoặc đội nào có thể thăng tiến trong bảng xếp hạng.

Dạng Bài Tập 3: Tính Toán Tỉ Lệ
Trong bài tập này, chúng ta sẽ tập trung vào việc tính toán tỉ lệ giữa các đội bóng dựa trên bảng xếp hạng. Để làm điều này, bạn cần phải hiểu rõ về cách xếp hạng của các đội trong giải đấu và cách tính toán điểm số của họ.
Để bắt đầu, hãy xem qua các thông số cơ bản mà chúng ta cần:
- Số trận thắng: Số trận đấu mà một đội bóng giành chiến thắng.
- Số trận hòa: Số trận đấu kết thúc với kết quả hòa.
- Số trận thua: Số trận đấu mà đội bóng thua cuộc.
- Hiệu số bàn thắng: Hiệu số giữa số bàn thắng ghi được và số bàn thua.
Dựa trên các thông số này, chúng ta có thể tính toán tỉ lệ thành công của một đội bóng theo công thức:
Ví dụ: Nếu một đội bóng đã chơi 30 trận, trong đó họ thắng 18 trận, hòa 6 trận và thua 6 trận, tỉ lệ thành công của đội bóng đó sẽ được tính như sau:
Chúng ta có thể phân tích các dữ liệu này để dự đoán vị trí của đội bóng trong bảng xếp hạng. Những phân tích này giúp xác định cơ hội của đội bóng trong các vòng đấu tiếp theo và chuẩn bị chiến lược thi đấu phù hợp.
Cuối cùng, sau khi hoàn thành các phép tính, bạn có thể so sánh tỉ lệ thành công của các đội bóng để đánh giá hiệu suất và vị trí của họ trên bảng xếp hạng.
XEM THÊM:
Dạng Bài Tập 4: Giải Bất Phương Trình
Dạng bài tập giải bất phương trình là một trong những nội dung cơ bản và quan trọng trong toán học. Để giải bất phương trình, chúng ta cần thực hiện các bước cơ bản dưới đây:
- Phân tích bất phương trình: Trước tiên, ta cần phân tích và đưa bất phương trình về dạng đơn giản nhất. Xác định các thành phần và thứ tự ưu tiên của các phép toán trong bất phương trình.
- Thực hiện phép biến đổi: Sau khi đã phân tích, ta thực hiện các phép biến đổi tương đương để đơn giản hóa bất phương trình. Chú ý rằng khi nhân hoặc chia cả hai vế của bất phương trình với một số âm, dấu bất phương trình sẽ bị đổi chiều.
- Giải và xác định nghiệm: Tiếp theo, ta giải bất phương trình đã đơn giản hóa và xác định miền giá trị của nghiệm.
- Lập bảng xét dấu: Với những bất phương trình phức tạp, ta cần lập bảng xét dấu để dễ dàng xác định miền giá trị của nghiệm một cách chính xác. Điều này giúp đảm bảo rằng ta không bỏ sót bất kỳ nghiệm nào.
- Kết luận và trình bày kết quả: Cuối cùng, ta viết lại kết quả nghiệm của bất phương trình theo cách rõ ràng và dễ hiểu. Nếu có nhiều nghiệm, hãy liệt kê tất cả các khoảng nghiệm một cách chi tiết.
Ví dụ minh họa:
Giải bất phương trình sau: \[ 2x + 3 > 5 \]
- Trừ 3 cả hai vế: \[ 2x > 2 \]
- Chia cả hai vế cho 2: \[ x > 1 \]
Vậy nghiệm của bất phương trình là \( x > 1 \).
Trong thực tế, việc giải bất phương trình có thể phức tạp hơn với nhiều bước biến đổi. Tuy nhiên, bằng cách tuân thủ các bước trên, chúng ta có thể giải quyết mọi bài toán liên quan đến bất phương trình một cách hiệu quả và chính xác.
Dạng Bài Tập 5: Đọc Hiểu Văn Bản Tiếng Anh
Trong dạng bài tập đọc hiểu văn bản tiếng Anh, học sinh cần nắm vững các kỹ năng cơ bản như đọc lướt, đọc kỹ, và phân tích ngữ cảnh. Dưới đây là các bước giúp bạn hoàn thành dạng bài tập này một cách hiệu quả:
- Đọc Lướt Toàn Bộ Văn Bản:
Trước tiên, hãy đọc lướt qua văn bản để nắm bắt ý chính và cấu trúc tổng quát. Chú ý đến tiêu đề, các đoạn văn và câu chủ đề.
- Đọc Kỹ Các Đoạn Văn:
Sau khi nắm được ý chính, đọc kỹ từng đoạn để hiểu sâu hơn về nội dung và các chi tiết quan trọng. Cần chú ý đến các từ khóa, cụm từ hoặc câu có thể là chìa khóa giải quyết câu hỏi.
- Phân Tích Ngữ Cảnh:
Khi gặp các từ mới hoặc các câu phức tạp, hãy dựa vào ngữ cảnh để đoán nghĩa và hiểu rõ hơn về ý định của tác giả. Đôi khi, nghĩa của từ hay câu không phải lúc nào cũng rõ ràng khi tách riêng lẻ, mà phải được hiểu trong ngữ cảnh tổng thể.
- Trả Lời Câu Hỏi:
Sau khi đã hiểu rõ văn bản, hãy trả lời các câu hỏi đi kèm. Hãy chắc chắn rằng mỗi câu trả lời đều dựa trên thông tin từ văn bản, và nếu có thể, trích dẫn lại một phần nhỏ của văn bản để làm rõ quan điểm.
Dưới đây là một ví dụ minh họa:
Ví dụ: Đọc đoạn văn sau và trả lời câu hỏi:
"The economic policies of the country have been a subject of debate for years. While some argue that they have led to increased prosperity, others believe they have widened the gap between the rich and the poor."
- Câu hỏi: What is the main argument presented in the text?
- Trả lời: The text presents two contrasting views on the country's economic policies: some believe they have increased prosperity, while others think they have widened the gap between rich and poor.
Thông qua quá trình luyện tập dạng bài tập này, học sinh sẽ phát triển được khả năng tư duy phân tích và hiểu sâu hơn về ngôn ngữ, từ đó tự tin hơn khi đối mặt với các kỳ thi quốc tế.

Dạng Bài Tập 6: Viết Đoạn Văn Ngắn Bằng Tiếng Anh
Trong dạng bài tập này, học sinh sẽ được yêu cầu viết một đoạn văn ngắn bằng tiếng Anh với các yêu cầu cụ thể về nội dung và ngữ pháp. Để thực hiện tốt dạng bài tập này, các bước dưới đây có thể được áp dụng:
-
Hiểu Đề Bài:
Trước hết, hãy đọc kỹ đề bài để xác định chủ đề và các yêu cầu cụ thể. Điều này giúp bạn xác định rõ nội dung đoạn văn cần viết.
-
Lập Dàn Ý:
Xác định những ý chính cần có trong đoạn văn. Thông thường, một đoạn văn ngắn sẽ có câu mở đầu, các câu hỗ trợ ý chính, và câu kết luận.
-
Viết Câu Mở Đầu:
Câu mở đầu nên nêu rõ chủ đề và đưa ra ý chính của đoạn văn. Hãy giữ cho câu này rõ ràng và ngắn gọn.
-
Phát Triển Ý Chính:
Sử dụng các câu hỗ trợ để phát triển ý chính của đoạn văn. Mỗi câu nên đưa ra một ý hỗ trợ cụ thể và liên kết với các câu khác.
-
Viết Câu Kết Luận:
Câu kết luận nên tóm tắt lại ý chính và có thể nêu ra quan điểm cá nhân nếu cần thiết. Câu này giúp kết thúc đoạn văn một cách mạch lạc.
-
Kiểm Tra Lại Đoạn Văn:
Cuối cùng, hãy đọc lại đoạn văn để kiểm tra lỗi chính tả, ngữ pháp và cấu trúc câu. Điều này đảm bảo đoạn văn hoàn chỉnh và không có lỗi sai.
Ví dụ:
Đề bài: Viết một đoạn văn ngắn về tầm quan trọng của thể thao trong cuộc sống.
- Câu mở đầu: Thể thao đóng vai trò quan trọng trong việc duy trì sức khỏe và tinh thần sảng khoái.
- Câu hỗ trợ 1: Tham gia thể thao giúp cải thiện sức khỏe thể chất, giảm nguy cơ mắc các bệnh như béo phì và cao huyết áp.
- Câu hỗ trợ 2: Thể thao còn giúp rèn luyện tinh thần, tạo cơ hội giao lưu và xây dựng kỹ năng làm việc nhóm.
- Câu kết luận: Như vậy, thể thao không chỉ là hoạt động giải trí mà còn mang lại nhiều lợi ích thiết thực cho cuộc sống hàng ngày.
Dạng Bài Tập 7: Tính Toán Lượng Giác
Dạng bài tập tính toán lượng giác là một trong những dạng bài quan trọng và thường gặp trong chương trình toán học, đặc biệt là trong các kỳ thi quan trọng. Để giải quyết tốt các bài toán lượng giác, học sinh cần nắm vững các công thức lượng giác cơ bản và các phương pháp biến đổi để áp dụng hiệu quả. Dưới đây là các bước cơ bản để giải quyết các dạng bài tập này.
-
Nhớ các công thức lượng giác cơ bản: Trước hết, học sinh cần ghi nhớ các công thức lượng giác cơ bản như:
- Công thức tính sin, cos, tan và cot:
- \(\sin A = \frac{đối}{huyền}\)
- \(\cos A = \frac{kề}{huyền}\)
- \(\tan A = \frac{đối}{kề}\)
- \(\cot A = \frac{kề}{đối}\)
- Các công thức cộng, nhân và biến đổi đơn giản:
- \(\sin(a \pm b) = \sin a \cos b \pm \cos a \sin b\)
- \(\cos(a \pm b) = \cos a \cos b \mp \sin a \sin b\)
- \(\tan(a \pm b) = \frac{\tan a \pm \tan b}{1 \mp \tan a \tan b}\)
-
Phân tích bài toán: Sau khi đã nhớ các công thức cơ bản, việc phân tích bài toán là bước tiếp theo. Học sinh cần xác định các góc lượng giác liên quan, các giá trị cần tính và chọn công thức phù hợp để giải quyết.
-
Áp dụng công thức và biến đổi: Ở bước này, học sinh sẽ áp dụng các công thức đã ghi nhớ và thực hiện các bước biến đổi cần thiết để đơn giản hóa biểu thức lượng giác. Trong một số trường hợp, có thể cần đến các phép biến đổi phức tạp hơn như biến đổi tổng thành tích, sử dụng các hệ thức lượng giác nâng cao.
-
Kiểm tra kết quả: Sau khi tính toán, học sinh nên kiểm tra lại kết quả để đảm bảo tính chính xác. Việc kiểm tra có thể bao gồm việc thay lại kết quả vào biểu thức ban đầu hoặc sử dụng các phương pháp khác nhau để giải quyết cùng một bài toán nhằm so sánh kết quả.
Việc luyện tập thường xuyên các bài tập lượng giác sẽ giúp học sinh nâng cao kỹ năng và đạt được kết quả tốt trong các kỳ thi. Điều quan trọng là cần nắm vững lý thuyết và áp dụng chúng một cách linh hoạt vào các bài tập cụ thể.

Dạng Bài Tập 8: Giải Toán Đố
Trong dạng bài tập này, chúng ta sẽ làm quen với các bài toán đố, một phần không thể thiếu trong việc phát triển tư duy và khả năng giải quyết vấn đề của học sinh. Các bài toán đố thường yêu cầu người học phải suy nghĩ sáng tạo và áp dụng các phương pháp toán học một cách linh hoạt để tìm ra lời giải.
Dưới đây là các bước cơ bản để giải quyết một bài toán đố:
- Đọc kỹ đề bài: Đây là bước đầu tiên và quan trọng nhất. Cần đọc kỹ đề bài để hiểu rõ yêu cầu và những thông tin đã cho.
- Phân tích đề bài: Sau khi hiểu rõ yêu cầu, cần xác định các dữ kiện quan trọng và tìm ra mối liên hệ giữa chúng. Nếu cần thiết, hãy vẽ sơ đồ hoặc biểu đồ để trực quan hóa vấn đề.
- Chọn phương pháp giải: Dựa trên các dữ kiện và mối liên hệ đã phân tích, chọn phương pháp giải thích hợp. Có thể là phương pháp lập phương trình, sử dụng công thức toán học, hoặc thậm chí là thử nghiệm và loại trừ.
- Giải quyết bài toán: Thực hiện các phép tính cần thiết để tìm ra đáp án.
- Kiểm tra lại kết quả: Sau khi có đáp án, cần kiểm tra lại các bước giải để đảm bảo rằng kết quả là chính xác và phù hợp với yêu cầu của đề bài.
Dưới đây là ví dụ minh họa cho một bài toán đố:
Ví dụ: Một lớp học có \(n\) học sinh, trong đó có \(m\) học sinh giỏi Toán và \(k\) học sinh giỏi Văn. Biết rằng số học sinh giỏi cả Toán và Văn là \(x\), hãy tính số học sinh giỏi Toán hoặc Văn.
Giải:
Để tính số học sinh giỏi Toán hoặc Văn, chúng ta sử dụng công thức sau:
Trong đó:
- \(S\): Số học sinh giỏi Toán hoặc Văn.
- \(m\): Số học sinh giỏi Toán.
- \(k\): Số học sinh giỏi Văn.
- \(x\): Số học sinh giỏi cả Toán và Văn.
Ví dụ, nếu \(m = 20\), \(k = 15\) và \(x = 5\), số học sinh giỏi Toán hoặc Văn sẽ là:
Như vậy, có 30 học sinh giỏi Toán hoặc Văn trong lớp học này.
Dạng bài toán đố không chỉ giúp học sinh phát triển kỹ năng giải toán mà còn rèn luyện tư duy logic và khả năng tư duy phản biện, điều rất quan trọng trong nhiều lĩnh vực khác nhau của cuộc sống.
Dạng Bài Tập 9: Thực Hành Phân Tích Cấu Trúc Câu Tiếng Anh
Trong dạng bài tập này, học sinh sẽ thực hành phân tích cấu trúc câu trong tiếng Anh để hiểu rõ cách các thành phần trong câu kết hợp với nhau. Việc phân tích cấu trúc câu không chỉ giúp cải thiện kỹ năng ngữ pháp mà còn nâng cao khả năng đọc hiểu và viết câu đúng chuẩn.
Bước 1: Xác định Chủ Ngữ (Subject)
Chủ ngữ là phần chính của câu, thường là danh từ hoặc cụm danh từ. Ví dụ:
- Câu: The quick brown fox jumps over the lazy dog.
- Chủ ngữ: The quick brown fox
Bước 2: Xác định Động Từ Chính (Main Verb)
Động từ chính là từ chỉ hành động hoặc trạng thái của chủ ngữ. Ví dụ:
- Câu: The quick brown fox jumps over the lazy dog.
- Động từ chính: jumps
Bước 3: Xác định Tân Ngữ (Object) (Nếu Có)
Tân ngữ là đối tượng mà hành động của động từ tác động đến. Ví dụ:
- Câu: The quick brown fox jumps over the lazy dog.
- Tân ngữ: the lazy dog
Bước 4: Xác định Các Thành Phần Khác (Nếu Có)
Các thành phần khác như trạng từ, giới từ, bổ ngữ, hoặc cụm từ bổ nghĩa có thể thêm thông tin chi tiết về hành động, thời gian, nơi chốn, hoặc cách thức. Ví dụ:
- Câu: The quick brown fox jumps over the lazy dog in the garden.
- Thành phần bổ sung: in the garden
Bước 5: Thực Hành Với Các Câu Khó Hơn
Sau khi nắm vững các bước trên, học sinh có thể thực hành với các câu phức tạp hơn, bao gồm cả câu ghép và câu phức, để phát triển kỹ năng phân tích cấu trúc câu một cách toàn diện. Ví dụ:
- Câu: The student who studied all night aced the exam because she understood the material thoroughly.
- Phân tích:
- Chủ ngữ: The student who studied all night
- Động từ chính: aced
- Tân ngữ: the exam
- Thành phần bổ sung: because she understood the material thoroughly
Bằng cách thực hành thường xuyên, học sinh sẽ ngày càng thành thạo trong việc nhận diện và phân tích cấu trúc câu, từ đó phát triển kỹ năng ngôn ngữ tiếng Anh của mình.
Dạng Bài Tập 10: Tìm Giới Hạn Của Dãy Số
Trong toán học, giới hạn của dãy số là một khái niệm cơ bản, đặc biệt quan trọng trong giải tích. Dưới đây là hướng dẫn chi tiết về cách tìm giới hạn của một dãy số, giúp bạn nắm vững phương pháp và áp dụng chúng vào các bài tập cụ thể.
- Bước 1: Hiểu khái niệm về giới hạn của dãy số
Giới hạn của một dãy số là giá trị mà dãy số đó tiến tới khi chỉ số của dãy tiến tới vô cực. Chúng ta ký hiệu giới hạn của dãy số \( \{a_n\} \) là \( \lim_{n \to \infty} a_n \).
- Bước 2: Xác định tính hội tụ hay phân kỳ của dãy
Một dãy số \( \{a_n\} \) được gọi là hội tụ nếu tồn tại một số \( L \) sao cho với mọi \( \epsilon > 0 \), tồn tại số nguyên \( N \) sao cho khi \( n > N \) thì \( |a_n - L| < \epsilon \). Ngược lại, nếu dãy không hội tụ, ta nói dãy phân kỳ.
- Bước 3: Sử dụng các phương pháp tìm giới hạn
- Phương pháp cơ bản: Dùng định nghĩa giới hạn, tức là kiểm tra điều kiện hội tụ theo định nghĩa trên.
- Phương pháp so sánh: So sánh dãy cần tìm giới hạn với một dãy số khác đã biết giới hạn.
- Phương pháp nhân tử: Biến đổi dãy số thành một dạng mà giới hạn dễ xác định hơn.
- Bước 4: Áp dụng vào các bài tập cụ thể
Hãy xem xét một ví dụ cụ thể: Tìm giới hạn của dãy số \( a_n = \frac{n^2 + 1}{2n^2 + 3} \).
Giải: Ta có thể nhận thấy rằng \( a_n \) có dạng phân thức hữu tỉ. Để tìm giới hạn, ta chia tử và mẫu cho \( n^2 \) (lũy thừa cao nhất trong mẫu số):
\[ a_n = \frac{\frac{n^2}{n^2} + \frac{1}{n^2}}{\frac{2n^2}{n^2} + \frac{3}{n^2}} = \frac{1 + \frac{1}{n^2}}{2 + \frac{3}{n^2}} \]Khi \( n \) tiến tới vô cực, các thành phần chứa \( \frac{1}{n^2} \) sẽ tiến về 0, do đó:
\[ \lim_{n \to \infty} a_n = \frac{1 + 0}{2 + 0} = \frac{1}{2} \]
Qua các bước trên, bạn đã có thể tự tin tìm giới hạn của các dãy số trong các bài tập toán học, đặc biệt là trong các kỳ thi quan trọng.