Chủ đề bảng xếp hạng fifa bóng đá nam the giới: Bảng xếp hạng FIFA bóng đá nam thế giới là thước đo quan trọng phản ánh phong độ của các đội tuyển quốc gia. Bài viết này cung cấp thông tin chi tiết về bảng xếp hạng mới nhất, những thay đổi đáng chú ý và phân tích sự thăng hạng, tụt hạng của các đội tuyển trên toàn cầu.
Mục lục
- Bảng Xếp Hạng FIFA Bóng Đá Nam Thế Giới - Cập Nhật Tháng 8 Năm 2024
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Về Toán Học
- Bài Tập 1: Giải Hệ Phương Trình Tuyến Tính
- Bài Tập 2: Tính Tích Phân Bằng Phương Pháp Đổi Biến
- Bài Tập 3: Giải Phương Trình Vi Phân Bậc Nhất
- Bài Tập 4: Tìm Cực Trị Của Hàm Số
- Bài Tập 5: Tính Đạo Hàm Của Hàm Số Phức
- Bài Tập 6: Giải Phương Trình Bậc Hai
- Bài Tập 7: Tính Xác Suất Trong Phép Thử Ngẫu Nhiên
- Bài Tập 8: Giải Bất Đẳng Thức
- Bài Tập 9: Phân Tích Ma Trận
- Bài Tập 10: Tìm Dãy Số Tăng Dần
Bảng Xếp Hạng FIFA Bóng Đá Nam Thế Giới - Cập Nhật Tháng 8 Năm 2024
Dưới đây là bảng xếp hạng FIFA bóng đá nam thế giới cập nhật mới nhất vào tháng 8 năm 2024. Bảng xếp hạng này phản ánh sự thay đổi điểm số của các đội tuyển quốc gia sau các trận đấu quốc tế.
Top 10 Đội Tuyển Quốc Gia
| Xếp Hạng | Đội Tuyển | Khu Vực | Điểm Số | Thay Đổi Điểm Số |
|---|---|---|---|---|
| 1 | Argentina | Nam Mỹ | 1901 | +41 |
| 2 | Pháp | Châu Âu | 1854 | +17 |
| 3 | Tây Ban Nha | Châu Âu | 1835 | +105 |
| 4 | Anh | Châu Âu | 1812 | +24 |
| 5 | Brazil | Nam Mỹ | 1785 | -6 |
| 6 | Bỉ | Châu Âu | 1772 | -25 |
| 7 | Hà Lan | Châu Âu | 1758 | +11 |
| 8 | Bồ Đào Nha | Châu Âu | 1741 | -5 |
| 9 | Colombia | Nam Mỹ | 1727 | +57 |
| 10 | Ý | Châu Âu | 1714 | -10 |
Thay Đổi Quan Trọng
- Tây Ban Nha thăng hạng mạnh mẽ với +105 điểm, chiếm vị trí thứ 3 trên bảng xếp hạng.
- Colombia có sự tăng trưởng đáng kể với +57 điểm, đạt hạng 9.
- Brazil và Bỉ có sự sụt giảm nhẹ trong điểm số, nhưng vẫn nằm trong top 10.
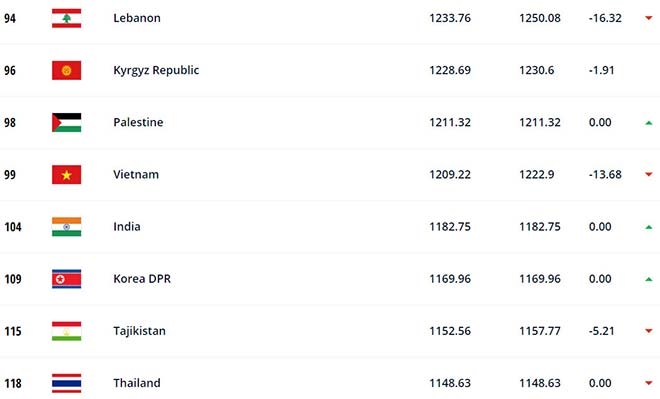
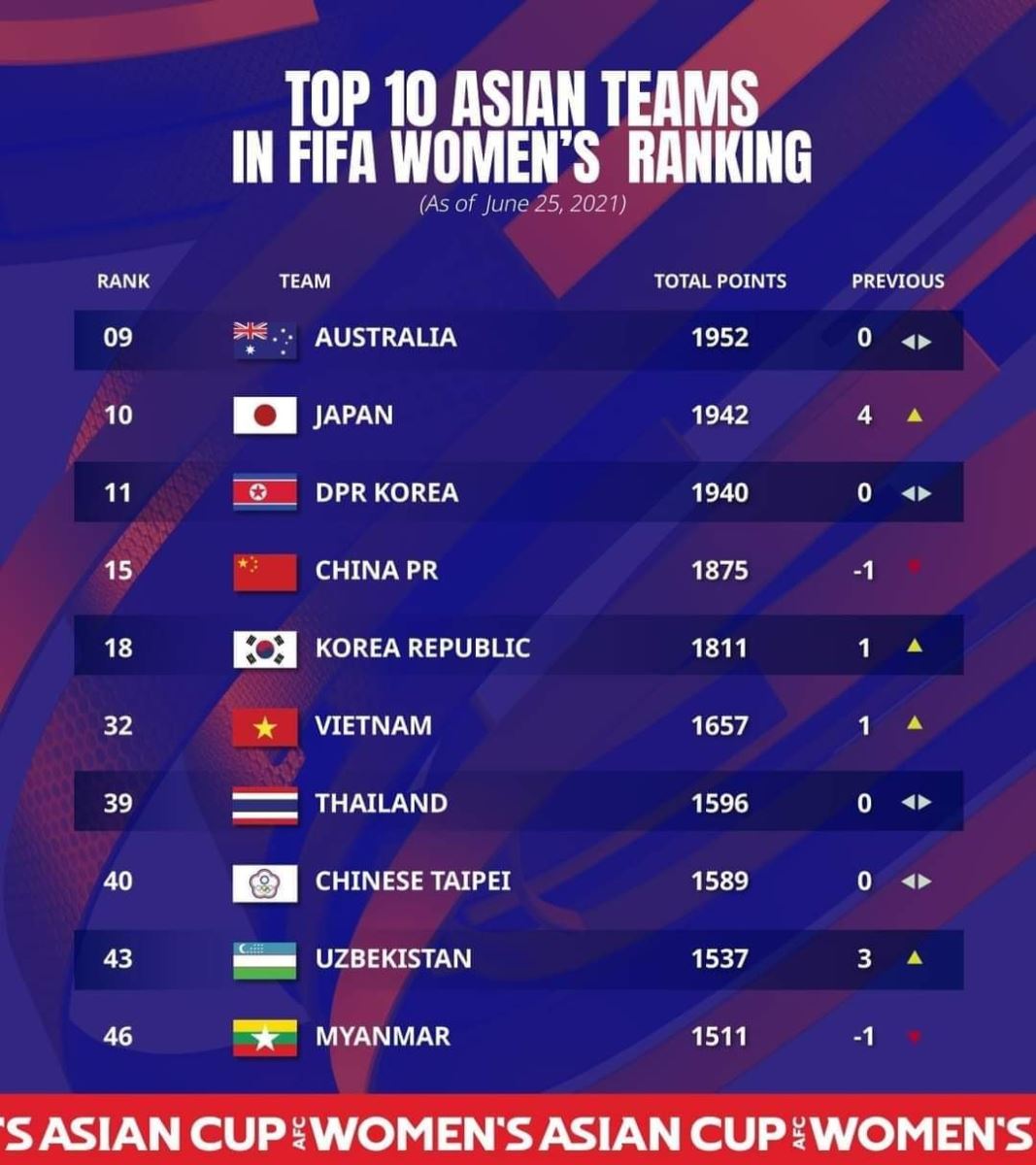
Các Đội Tuyển Châu Á Nổi Bật
| Xếp Hạng | Đội Tuyển | Điểm Số | Thay Đổi Điểm Số |
|---|---|---|---|
| 18 | Nhật Bản | 1628 | +0 |
| 20 | Iran | 1611 | +0 |
| 23 | Hàn Quốc | 1572 | +0 |
Các đội tuyển châu Á như Nhật Bản, Iran và Hàn Quốc duy trì vị trí ổn định trong top 30. Đây là những đội tuyển có tiềm năng lớn và đang được đánh giá cao trong các giải đấu quốc tế.

.png)
Mục Lục Tổng Hợp
Dưới đây là mục lục tổng hợp chi tiết về bảng xếp hạng FIFA bóng đá nam thế giới, cập nhật mới nhất với các thông tin quan trọng về các đội tuyển hàng đầu và sự thay đổi vị trí trên bảng xếp hạng.
- Giới Thiệu Về Bảng Xếp Hạng FIFA Bóng Đá Nam Thế Giới
- Tổng quan về bảng xếp hạng FIFA
- Tầm quan trọng của bảng xếp hạng đối với các đội tuyển quốc gia
- Cách Tính Điểm Và Quy Tắc Xếp Hạng Của FIFA
- Phương pháp tính điểm của FIFA
- Quy tắc xếp hạng các đội tuyển quốc gia
- Top 10 Đội Tuyển Hàng Đầu Trên Bảng Xếp Hạng FIFA
- Các đội tuyển đứng đầu bảng xếp hạng FIFA
- Phân tích sự thay đổi vị trí của các đội tuyển
- Thay Đổi Quan Trọng Trên Bảng Xếp Hạng FIFA Tháng 8/2024
- Những đội tuyển thăng hạng mạnh mẽ
- Những đội tuyển tụt hạng đáng chú ý
- Các Đội Tuyển Châu Á Trên Bảng Xếp Hạng FIFA
- Vị trí của các đội tuyển châu Á như Nhật Bản, Hàn Quốc, Iran
- Đánh giá tiềm năng của các đội tuyển châu Á
- Ảnh Hưởng Của Bảng Xếp Hạng FIFA Đến Các Giải Đấu Quốc Tế
- Tác động đến việc phân hạng các đội tuyển trong các giải đấu lớn
- Cách bảng xếp hạng ảnh hưởng đến chiến lược thi đấu
- Dự Đoán Xu Hướng Thay Đổi Của Bảng Xếp Hạng FIFA
- Dự đoán về phong độ của các đội tuyển trong tương lai
- Những yếu tố có thể ảnh hưởng đến bảng xếp hạng
- Lịch Sử Phát Triển Của Bảng Xếp Hạng FIFA
- Quá trình phát triển từ khi thành lập đến nay
- Những thay đổi lớn trong quy tắc xếp hạng
- Phân Tích Chi Tiết Về Điểm Số Của Một Số Đội Tuyển Mới Thăng Hạng
- Phân tích sự thăng hạng của các đội tuyển mới nổi
- Yếu tố góp phần vào sự thành công của các đội tuyển này
- Những Đội Tuyển Quốc Gia Có Sự Tụt Hạng Lớn Trong Bảng Xếp Hạng FIFA
- Nguyên nhân tụt hạng của một số đội tuyển
- Ảnh hưởng của việc tụt hạng đến các đội tuyển
10 Dạng Bài Tập Về Toán Học
Dưới đây là 10 dạng bài tập toán học phổ biến, mỗi bài tập được thiết kế để rèn luyện các kỹ năng và tư duy toán học của học sinh ở các cấp độ khác nhau. Mỗi dạng bài tập đều có lời giải chi tiết để giúp người học hiểu rõ hơn về các khái niệm và phương pháp giải toán.
- Giải Phương Trình Tuyến Tính
Giải các phương trình dạng \( ax + b = 0 \) và các bài toán liên quan đến việc xác định nghiệm của phương trình tuyến tính.
- Tìm Cực Trị Của Hàm Số
Sử dụng đạo hàm để xác định điểm cực đại, cực tiểu của các hàm số đơn giản và phức tạp.
- Tính Tích Phân Bằng Phương Pháp Đổi Biến
Thực hành tính tích phân của các hàm số bằng cách sử dụng phương pháp đổi biến và các kỹ thuật tích phân cơ bản.
- Giải Hệ Phương Trình Tuyến Tính Nhiều Ẩn
Giải hệ phương trình có nhiều ẩn số bằng phương pháp cộng đại số và phương pháp Gauss.
- Giải Bất Đẳng Thức
Sử dụng các định lý và tính chất của bất đẳng thức để giải các bài toán bất đẳng thức cơ bản và nâng cao.
- Tính Xác Suất Trong Phép Thử Ngẫu Nhiên
Tính xác suất của các sự kiện trong một phép thử ngẫu nhiên, áp dụng lý thuyết xác suất vào các bài toán thực tế.
- Phân Tích Ma Trận Và Định Thức
Phân tích các ma trận, tính định thức và ứng dụng của chúng trong việc giải hệ phương trình tuyến tính.
- Giải Phương Trình Vi Phân Bậc Nhất
Giải các phương trình vi phân bậc nhất bằng phương pháp biến phân và phương pháp tách biến.
- Tìm Đạo Hàm Của Hàm Số Phức
Tính đạo hàm của các hàm số phức và giải các bài toán liên quan đến tính chất của hàm số phức.
- Phân Tích Dãy Số Và Tìm Tổng Dãy
Phân tích dãy số, tính tổng dãy và các bài toán liên quan đến dãy số trong toán học.

Bài Tập 1: Giải Hệ Phương Trình Tuyến Tính
Bài toán này yêu cầu bạn giải hệ phương trình tuyến tính với hai hoặc nhiều ẩn số. Hệ phương trình tuyến tính là một hệ gồm nhiều phương trình, trong đó mỗi phương trình đều là phương trình bậc nhất theo các ẩn.
Giả sử chúng ta có hệ phương trình tuyến tính sau:
Để giải hệ phương trình này, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Dưới đây là các bước chi tiết để giải hệ phương trình bằng phương pháp cộng đại số:
- Bước 1: Nhân các phương trình với các hệ số thích hợp để làm cho một trong các biến có cùng hệ số đối nhau (nghĩa là, cộng vào sẽ triệt tiêu biến đó).
- Bước 2: Cộng hoặc trừ hai phương trình để loại bỏ một biến, từ đó thu được một phương trình chỉ chứa một biến duy nhất.
- Bước 3: Giải phương trình đơn biến để tìm giá trị của biến đầu tiên.
- Bước 4: Thay giá trị của biến đầu tiên vừa tìm được vào một trong hai phương trình ban đầu để giải biến thứ hai.
- Bước 5: Viết nghiệm của hệ phương trình dưới dạng cặp \((x, y)\).
Ví dụ, với hệ phương trình:
Thực hiện các bước như trên sẽ giúp chúng ta tìm ra nghiệm của hệ phương trình là \((x, y) = (1, 1)\).

Bài Tập 2: Tính Tích Phân Bằng Phương Pháp Đổi Biến
Bài toán này yêu cầu bạn tính tích phân của một hàm số bằng phương pháp đổi biến. Phương pháp đổi biến giúp đơn giản hóa quá trình tính toán tích phân bằng cách thay thế biến số ban đầu bằng một biến số mới, làm cho hàm tích phân trở nên đơn giản hơn.
Giả sử chúng ta cần tính tích phân sau:
Để giải quyết bài toán này, ta có thể thực hiện các bước sau:
- Bước 1: Đặt \( u = x^2 + 1 \), do đó \( du = 2x \, dx \).
- Bước 2: Thay vào tích phân ban đầu để đơn giản hóa nó. Khi đó, tích phân trở thành: \[ \frac{1}{2} \int \sqrt{u} \, du \]
- Bước 3: Tính tích phân của hàm số mới: \[ \frac{1}{2} \cdot \frac{2}{3} u^{3/2} = \frac{1}{3} u^{3/2} \]
- Bước 4: Thay \( u \) bằng \( x^2 + 1 \) để trở về biến số ban đầu: \[ \frac{1}{3} (x^2 + 1)^{3/2} + C \]
- Bước 5: Ghi kết quả cuối cùng: \[ \int x \sqrt{x^2 + 1} \, dx = \frac{1}{3} (x^2 + 1)^{3/2} + C \]
Với các bước trên, ta đã hoàn thành việc tính tích phân của hàm số bằng phương pháp đổi biến.

Bài Tập 3: Giải Phương Trình Vi Phân Bậc Nhất
Bài toán này yêu cầu bạn giải phương trình vi phân bậc nhất. Phương trình vi phân bậc nhất có dạng tổng quát:
Trong đó, \( P(x) \) và \( Q(x) \) là các hàm số liên quan đến \( x \). Để giải phương trình này, ta có thể sử dụng phương pháp tích phân nhân, với các bước thực hiện như sau:
- Bước 1: Xác định hàm số tích phân nhân \( \mu(x) \) bằng cách tính: \[ \mu(x) = e^{\int P(x) \, dx} \]
- Bước 2: Nhân toàn bộ phương trình vi phân ban đầu với \( \mu(x) \) để phương trình trở thành: \[ \mu(x) \frac{dy}{dx} + \mu(x)P(x)y = \mu(x)Q(x) \]
- Bước 3: Nhận thấy rằng vế trái của phương trình là đạo hàm của tích \( \mu(x)y \), do đó ta viết lại phương trình dưới dạng: \[ \frac{d}{dx}[\mu(x)y] = \mu(x)Q(x) \]
- Bước 4: Tích phân cả hai vế của phương trình theo \( x \) để tìm \( y(x) \): \[ \mu(x)y = \int \mu(x)Q(x) \, dx + C \]
- Bước 5: Cuối cùng, ta giải được hàm số \( y(x) \) bằng cách chia cả hai vế cho \( \mu(x) \): \[ y(x) = \frac{1}{\mu(x)} \left[\int \mu(x)Q(x) \, dx + C \right] \]
Ví dụ, với phương trình vi phân:
Thực hiện các bước như trên sẽ giúp chúng ta tìm ra nghiệm của phương trình vi phân bậc nhất này.
XEM THÊM:
Bài Tập 4: Tìm Cực Trị Của Hàm Số
Trong toán học, việc tìm cực trị của hàm số là một trong những bài toán quan trọng và thường gặp. Cực trị của hàm số gồm có cực đại và cực tiểu. Để tìm cực trị của hàm số, chúng ta có thể thực hiện các bước sau đây:
-
Bước 1: Tính đạo hàm cấp 1 của hàm số
Giả sử hàm số cần tìm cực trị là \( f(x) \). Trước tiên, chúng ta cần tính đạo hàm cấp 1 của hàm số, ký hiệu là \( f'(x) \).
\[
f'(x) = \frac{d}{dx}f(x)
\] -
Bước 2: Tìm các điểm nghi ngờ là cực trị
Ta giải phương trình \( f'(x) = 0 \) để tìm các điểm mà tại đó đạo hàm bằng 0. Các điểm này là các điểm nghi ngờ có cực trị.
-
Bước 3: Xét dấu đạo hàm cấp 1 để xác định cực trị
Sau khi tìm được các điểm \( x_0 \) thỏa mãn \( f'(x_0) = 0 \), chúng ta xét dấu của đạo hàm cấp 1 \( f'(x) \) trước và sau các điểm này.
- Nếu \( f'(x) \) đổi dấu từ dương sang âm khi đi qua \( x_0 \), thì \( x_0 \) là điểm cực đại.
- Nếu \( f'(x) \) đổi dấu từ âm sang dương khi đi qua \( x_0 \), thì \( x_0 \) là điểm cực tiểu.
-
Bước 4: Tính giá trị cực trị
Cuối cùng, để tìm giá trị cực trị, ta thay giá trị của \( x_0 \) vào hàm số ban đầu \( f(x) \) để tìm giá trị \( y_0 = f(x_0) \).
Ví dụ minh họa: Tìm cực trị của hàm số \( f(x) = x^3 - 3x^2 + 4 \).
- Bước 1: Tính đạo hàm cấp 1:
\[
f'(x) = 3x^2 - 6x
\] - Bước 2: Tìm các điểm nghi ngờ là cực trị bằng cách giải phương trình:
\[
3x^2 - 6x = 0
\]Giải phương trình này ta được: \( x_1 = 0 \), \( x_2 = 2 \).
- Bước 3: Xét dấu của \( f'(x) \):
- Với \( x < 0 \), \( f'(x) > 0 \), hàm số đồng biến.
- Với \( 0 < x < 2 \), \( f'(x) < 0 \), hàm số nghịch biến.
- Với \( x > 2 \), \( f'(x) > 0 \), hàm số đồng biến.
Vậy \( x_1 = 0 \) là điểm cực đại, \( x_2 = 2 \) là điểm cực tiểu.
- Bước 4: Tính giá trị cực trị:
- Giá trị cực đại: \( y_1 = f(0) = 4 \).
- Giá trị cực tiểu: \( y_2 = f(2) = -4 \).

Bài Tập 5: Tính Đạo Hàm Của Hàm Số Phức
Trong bài tập này, chúng ta sẽ đi tìm hiểu cách tính đạo hàm của hàm số phức \(f(z)\), trong đó \(z = x + iy\) với \(x, y\) là các số thực và \(i\) là đơn vị ảo, \(i^2 = -1\).
Bước 1: Xác định hàm số phức
Giả sử hàm số phức \(f(z)\) được xác định bởi:
\[
f(z) = u(x, y) + iv(x, y)
\]
Trong đó, \(u(x, y)\) và \(v(x, y)\) là các hàm số thực của hai biến \(x\) và \(y\).
Bước 2: Điều kiện Cauchy-Riemann
Để hàm số phức \(f(z)\) có đạo hàm, các hàm số \(u(x, y)\) và \(v(x, y)\) phải thỏa mãn điều kiện Cauchy-Riemann:
\[
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \quad \text{và} \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
\]
Bước 3: Tính đạo hàm của hàm số phức
Nếu các điều kiện Cauchy-Riemann thỏa mãn, đạo hàm của hàm số phức \(f(z)\) tại điểm \(z_0\) được tính bằng:
\[
f'(z_0) = \lim_{\Delta z \to 0} \frac{f(z_0 + \Delta z) - f(z_0)}{\Delta z}
\]
Ví dụ:
Giả sử \(f(z) = z^2\), với \(z = x + iy\). Ta có:
\[
f(z) = (x + iy)^2 = x^2 - y^2 + 2ixy
\]
Ở đây, \(u(x, y) = x^2 - y^2\) và \(v(x, y) = 2xy\). Chúng ta kiểm tra điều kiện Cauchy-Riemann:
\[
\frac{\partial u}{\partial x} = 2x, \quad \frac{\partial v}{\partial y} = 2x
\]
\[
\frac{\partial u}{\partial y} = -2y, \quad \frac{\partial v}{\partial x} = 2y
\]
Điều kiện Cauchy-Riemann thỏa mãn, do đó hàm \(f(z)\) có đạo hàm và đạo hàm của nó là:
\[
f'(z) = 2z
\]
Vậy đạo hàm của hàm số phức \(f(z) = z^2\) là \(f'(z) = 2z\).

Bài Tập 6: Giải Phương Trình Bậc Hai
Trong toán học, phương trình bậc hai là một dạng phương trình đa thức có dạng tổng quát:
\[ ax^2 + bx + c = 0 \]
Trong đó:
- \(a\), \(b\), và \(c\) là các hệ số với \(a \neq 0\).
- \(x\) là biến cần tìm.
Để giải phương trình bậc hai, ta có thể sử dụng công thức nghiệm sau:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Quy trình giải phương trình bậc hai qua các bước cụ thể như sau:
- Xác định các hệ số \(a\), \(b\), và \(c\) từ phương trình.
- Tính discriminant \( \Delta = b^2 - 4ac \).
- Xét dấu của discriminant để tìm nghiệm:
- Nếu \( \Delta > 0 \): Phương trình có hai nghiệm phân biệt.
- Nếu \( \Delta = 0 \): Phương trình có một nghiệm kép.
- Nếu \( \Delta < 0 \): Phương trình vô nghiệm (trong tập số thực).
- Sử dụng công thức trên để tìm nghiệm tương ứng.
Ví dụ: Giải phương trình bậc hai sau:
\[ 2x^2 - 4x + 2 = 0 \]
- Xác định hệ số: \(a = 2\), \(b = -4\), và \(c = 2\).
- Tính discriminant: \( \Delta = (-4)^2 - 4(2)(2) = 16 - 16 = 0 \).
- Vì \( \Delta = 0 \), phương trình có một nghiệm kép.
- Tính nghiệm: \( x = \frac{-(-4)}{2(2)} = \frac{4}{4} = 1 \).
Kết luận: Phương trình \( 2x^2 - 4x + 2 = 0 \) có nghiệm kép \( x = 1 \).
Bài Tập 7: Tính Xác Suất Trong Phép Thử Ngẫu Nhiên
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính xác suất trong các phép thử ngẫu nhiên. Xác suất là một nhánh của toán học, giúp ta đo lường khả năng xảy ra của một sự kiện trong một phép thử ngẫu nhiên.
1. Định nghĩa xác suất
Xác suất của một sự kiện \( A \) trong một không gian mẫu \( S \) được định nghĩa là:
\[
P(A) = \frac{\text{Số kết quả thuận lợi cho } A}{\text{Tổng số kết quả có thể xảy ra trong không gian mẫu } S}
\]
Với \( 0 \leq P(A) \leq 1 \), trong đó:
- \( P(A) = 0 \): Sự kiện không bao giờ xảy ra.
- \( P(A) = 1 \): Sự kiện chắc chắn xảy ra.
2. Phép thử ngẫu nhiên
Một phép thử ngẫu nhiên là một thí nghiệm hoặc một quan sát mà kết quả không thể được dự đoán chắc chắn. Mỗi kết quả có thể xảy ra trong phép thử này gọi là một khả năng.
3. Các dạng xác suất thường gặp
- Xác suất cổ điển: Áp dụng cho các phép thử có số khả năng hữu hạn, với tất cả các khả năng đều có cơ hội xảy ra như nhau.
- Xác suất thống kê: Áp dụng khi tính xác suất dựa trên số liệu thực nghiệm, được tính bằng tỷ lệ của số lần sự kiện xảy ra so với tổng số lần thực hiện phép thử.
- Xác suất chủ quan: Được ước tính dựa trên kinh nghiệm hoặc phán đoán cá nhân.
4. Ví dụ minh họa
Giả sử chúng ta có một phép thử ngẫu nhiên là gieo một đồng xu cân đối. Không gian mẫu \( S \) bao gồm hai khả năng: \( \{ \text{Ngửa}, \text{Sấp} \} \). Nếu chúng ta muốn tính xác suất của sự kiện \( A \) là xuất hiện mặt ngửa, ta có:
\[
P(\text{Ngửa}) = \frac{1}{2} = 0.5
\]
Do đó, xác suất xuất hiện mặt ngửa khi gieo một đồng xu là 0.5.
5. Tính xác suất của các sự kiện phức tạp hơn
Đối với các sự kiện phức tạp hơn như sự kiện liên quan đến nhiều phép thử ngẫu nhiên, chúng ta có thể sử dụng các quy tắc như quy tắc cộng và quy tắc nhân của xác suất:
- Quy tắc cộng: Dùng để tính xác suất của sự kiện \( A \) hoặc \( B \) xảy ra, ký hiệu là \( P(A \cup B) \).
- Quy tắc nhân: Dùng để tính xác suất của sự kiện \( A \) và \( B \) cùng xảy ra, ký hiệu là \( P(A \cap B) \).
6. Bài tập thực hành
Áp dụng các quy tắc trên để giải quyết các bài toán xác suất phức tạp. Ví dụ: Tính xác suất xuất hiện ít nhất một mặt ngửa khi gieo hai đồng xu.
Giải:
Không gian mẫu cho phép thử này là \( S = \{ (\text{Ngửa}, \text{Ngửa}), (\text{Ngửa}, \text{Sấp}), (\text{Sấp}, \text{Ngửa}), (\text{Sấp}, \text{Sấp}) \} \). Có 3 kết quả thuận lợi cho sự kiện ít nhất một mặt ngửa:
\[
P(\text{ít nhất một mặt ngửa}) = \frac{3}{4} = 0.75
\]
Vậy xác suất xuất hiện ít nhất một mặt ngửa khi gieo hai đồng xu là 0.75.
Bài Tập 8: Giải Bất Đẳng Thức
Bất đẳng thức là một phần quan trọng trong toán học, đặc biệt trong các bài toán ứng dụng. Việc giải bất đẳng thức giúp chúng ta tìm ra các giá trị của biến số thoả mãn điều kiện cho trước. Dưới đây là các bước cơ bản để giải một bất đẳng thức.
- Xác định loại bất đẳng thức: Đầu tiên, bạn cần xác định bất đẳng thức thuộc loại nào, ví dụ như bất đẳng thức tuyến tính, bất đẳng thức bậc hai, hoặc bất đẳng thức chứa giá trị tuyệt đối.
- Chuyển đổi bất đẳng thức: Tương tự như giải phương trình, bạn cần thực hiện các phép biến đổi như cộng, trừ, nhân, chia hai vế của bất đẳng thức. Lưu ý, khi nhân hoặc chia cả hai vế của bất đẳng thức với một số âm, dấu của bất đẳng thức sẽ thay đổi.
- Tìm nghiệm: Giải bất đẳng thức bằng cách tìm các giá trị của biến số thoả mãn điều kiện của bất đẳng thức. Đối với bất đẳng thức bậc hai, bạn có thể dùng phương pháp phân tích thành nhân tử hoặc dùng công thức nghiệm.
- Biểu diễn nghiệm: Sau khi tìm được nghiệm, bạn nên biểu diễn nghiệm trên trục số hoặc dưới dạng khoảng (nếu có nhiều nghiệm).
Ví dụ, xét bất đẳng thức bậc hai:
Để giải, ta thực hiện các bước sau:
- Tính biệt thức (Δ): \(\Delta = b^2 - 4ac\). Nếu Δ > 0, bất đẳng thức có hai nghiệm phân biệt.
- Xác định khoảng nghiệm: Xác định các khoảng trên trục số mà bất đẳng thức thỏa mãn dựa trên dấu của tam thức.
- Kết luận: Đưa ra kết luận về nghiệm của bất đẳng thức.
Việc giải bất đẳng thức đòi hỏi sự chính xác trong từng bước biến đổi và tính toán. Hãy luôn kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.
Bài Tập 9: Phân Tích Ma Trận
Phân tích ma trận là một kỹ thuật quan trọng trong đại số tuyến tính, giúp giải quyết nhiều bài toán trong các lĩnh vực khác nhau như vật lý, kinh tế, và khoa học máy tính. Dưới đây là hướng dẫn chi tiết từng bước để giải một bài toán phân tích ma trận.
- Xác định ma trận cần phân tích:
Giả sử chúng ta có ma trận \( A \) cỡ \( m \times n \). Trước tiên, chúng ta cần xác định rõ ma trận này và kiểm tra các tính chất của nó, như định thức và hạng của ma trận.
- Phân tích thành ma trận thành các thành phần:
Ma trận có thể được phân tích thành các thành phần chính như sau:
- Phân tích LU: Ma trận \( A \) được phân tích thành tích của một ma trận tam giác dưới \( L \) và một ma trận tam giác trên \( U \), tức là \( A = LU \).
- Phân tích Cholesky: Nếu ma trận \( A \) là ma trận vuông và xác định dương, ta có thể phân tích nó thành tích của một ma trận tam giác dưới và ma trận chuyển vị của nó: \( A = LL^T \).
- Phân tích Eigen: Ma trận \( A \) có thể được phân tích thông qua các giá trị riêng và vector riêng: \( A = PDP^{-1} \), trong đó \( P \) là ma trận các vector riêng và \( D \) là ma trận chéo các giá trị riêng.
- Kiểm tra kết quả:
Sau khi thực hiện các bước phân tích, hãy kiểm tra lại kết quả bằng cách nhân các ma trận thành phần với nhau để đảm bảo rằng chúng khớp với ma trận ban đầu \( A \).
- Ứng dụng của phân tích ma trận:
Phân tích ma trận có nhiều ứng dụng trong thực tế, ví dụ như trong giải hệ phương trình tuyến tính, tối ưu hóa, và phân tích dữ liệu.
Phân tích ma trận là một công cụ mạnh mẽ, và hiểu rõ quy trình phân tích sẽ giúp bạn áp dụng nó một cách hiệu quả trong nhiều bài toán khác nhau.
Bài Tập 10: Tìm Dãy Số Tăng Dần
Tìm dãy số tăng dần là một bài toán cơ bản nhưng quan trọng trong toán học, đặc biệt là trong lĩnh vực tối ưu hóa và giải thuật. Dưới đây là hướng dẫn từng bước để tìm dãy số tăng dần từ một tập hợp số cho trước.
- Xác định dãy số ban đầu:
Cho một dãy số \( a_1, a_2, a_3, \dots, a_n \). Nhiệm vụ của chúng ta là tìm một dãy con gồm các phần tử của dãy này sao cho dãy con đó có thứ tự tăng dần.
- Áp dụng thuật toán tìm dãy con tăng dần dài nhất (LIS):
Thuật toán LIS (Longest Increasing Subsequence) là phương pháp hiệu quả nhất để tìm dãy con tăng dần dài nhất. Thuật toán có thể được thực hiện như sau:
- Bước 1: Khởi tạo một mảng \( \text{LIS}[n] \) với tất cả các giá trị ban đầu bằng 1. Mỗi phần tử \( \text{LIS}[i] \) sẽ lưu độ dài của dãy con tăng dần kết thúc tại vị trí \( i \).
- Bước 2: Duyệt qua dãy số từ trái sang phải, với mỗi phần tử \( a[i] \), kiểm tra tất cả các phần tử trước đó \( a[j] \) với \( j < i \). Nếu \( a[i] > a[j] \), cập nhật \( \text{LIS}[i] = \max(\text{LIS}[i], \text{LIS}[j] + 1) \).
- Bước 3: Giá trị lớn nhất trong mảng \( \text{LIS} \) chính là độ dài của dãy con tăng dần dài nhất.
- Truy xuất dãy số tăng dần:
Sau khi tìm được độ dài của dãy con tăng dần dài nhất, bạn có thể truy xuất dãy con này bằng cách duyệt ngược lại dãy số từ vị trí có giá trị LIS lớn nhất.
- Ví dụ minh họa:
Cho dãy số \( 3, 10, 2, 1, 20 \). Sử dụng thuật toán LIS:
- Bước 1: Khởi tạo \( \text{LIS}[ ] = [1, 1, 1, 1, 1] \).
- Bước 2: Duyệt qua các phần tử và cập nhật \( \text{LIS} \):
- Tại vị trí \( i=2 \) (giá trị 10): \( \text{LIS}[2] = 2 \) vì 10 > 3.
- Tại vị trí \( i=3 \) (giá trị 2): Không thay đổi vì 2 không lớn hơn các giá trị trước đó.
- Tại vị trí \( i=4 \) (giá trị 1): Không thay đổi.
- Tại vị trí \( i=5 \) (giá trị 20): \( \text{LIS}[5] = 3 \) vì 20 > 10.
- Bước 3: Dãy con tăng dần dài nhất là \( 3, 10, 20 \) với độ dài 3.
Phương pháp này giúp bạn không chỉ tìm dãy con tăng dần dài nhất mà còn hiểu rõ cách thức xử lý bài toán thông qua lập trình và thuật toán.