Chủ đề bóng rổ cao su: Bóng rổ cao su là sự lựa chọn hoàn hảo cho cả người mới bắt đầu và người chơi chuyên nghiệp. Với chất liệu bền bỉ, khả năng chống mài mòn và giá thành hợp lý, bóng rổ cao su mang lại trải nghiệm tuyệt vời trên sân. Tìm hiểu ngay các loại bóng rổ cao su tốt nhất trên thị trường để nâng cao kỹ năng chơi của bạn.
Mục lục
- Bóng Rổ Cao Su - Thông Tin Chi Tiết và Hữu Ích
- Mục Lục
- Bài Tập Thực Hành Toán Liên Quan Đến Bóng Rổ Cao Su
- Bài Tập 1: Tính diện tích mặt bóng rổ
- Bài Tập 2: Tính thể tích bóng rổ
- Bài Tập 3: Tính khối lượng của bóng rổ
- Bài Tập 4: So sánh tốc độ bay của các loại bóng rổ
- Bài Tập 5: Tính lực cản của không khí lên bóng rổ
- Bài Tập 6: Tính khoảng cách bay của bóng rổ
- Bài Tập 7: Tính thời gian bay của bóng rổ
- Bài Tập 8: Tính áp lực bên trong bóng rổ
- Bài Tập 9: Tính công suất khi ném bóng
- Bài Tập 10: Tính động năng của bóng rổ khi ném
Bóng Rổ Cao Su - Thông Tin Chi Tiết và Hữu Ích
Bóng rổ cao su là một sản phẩm phổ biến dành cho những người yêu thích môn bóng rổ, đặc biệt là trong môi trường tập luyện ngoài trời. Đây là một loại bóng được sản xuất từ cao su chất lượng cao, có khả năng chống mài mòn tốt và giá thành hợp lý. Các thương hiệu nổi tiếng như Molten, GeruStar, Peak thường cung cấp các loại bóng rổ cao su với nhiều kích thước khác nhau, từ số 5 đến số 7.
Các Đặc Điểm Nổi Bật Của Bóng Rổ Cao Su
- Chất liệu cao su bền bỉ, có khả năng chống mài mòn tốt, đặc biệt phù hợp với sân bê tông hoặc sân ngoài trời.
- Khả năng chống thấm nước, giúp bóng duy trì độ bền và độ nảy ổn định trong điều kiện ẩm ướt.
- Giá thành hợp lý, phù hợp với người mới tập luyện cũng như người chơi không chuyên.
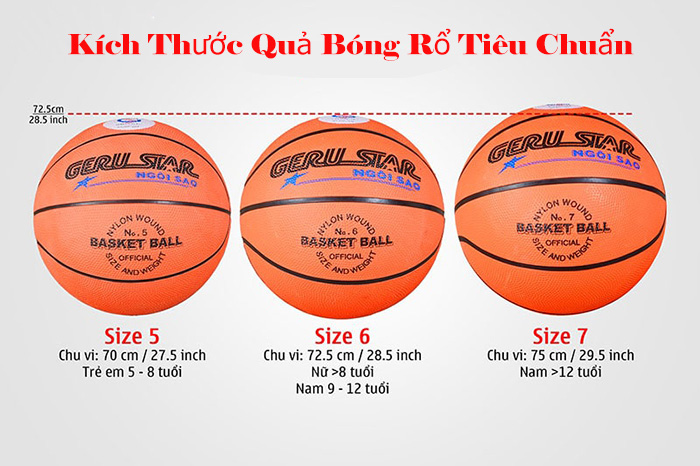
- Có nhiều kích thước khác nhau, phù hợp cho các độ tuổi và cấp độ người chơi: số 5 (trẻ em), số 6 (phụ nữ, thiếu niên), số 7 (nam giới, người chơi chuyên nghiệp).
Các Thương Hiệu Bóng Rổ Cao Su Nổi Tiếng
| Thương Hiệu | Giá Bán (VNĐ) | Đặc Điểm |
|---|---|---|
| Molten | 299,000 - 339,000 | Chất liệu cao su bền bỉ, chống thấm nước tốt. Được sử dụng rộng rãi trên toàn cầu. |
| GeruStar | 99,000 - 119,000 | Thương hiệu Việt Nam, chất lượng cao, giá thành hợp lý, phù hợp cho người mới tập chơi. |
| Peak | 449,000 | Sản phẩm cao cấp, thiết kế đẹp, bền và cho trải nghiệm chơi bóng tốt. |
Cách Chọn Bóng Rổ Cao Su Phù Hợp
Khi chọn bóng rổ cao su, bạn cần lưu ý đến các yếu tố sau:
- Kích thước bóng: Chọn đúng kích thước phù hợp với độ tuổi và giới tính của người chơi. Ví dụ, số 5 dành cho trẻ em, số 6 cho phụ nữ và thiếu niên, số 7 cho nam giới trưởng thành.
- Chất liệu: Bóng rổ cao su nên có độ đàn hồi tốt, khả năng chống thấm nước và độ bền cao để sử dụng trong các điều kiện sân ngoài trời.
- Thương hiệu: Nên chọn các thương hiệu uy tín như Molten, GeruStar để đảm bảo chất lượng.
- Giá cả: Phụ thuộc vào nhu cầu sử dụng và ngân sách cá nhân. Các sản phẩm có giá từ 100,000 đến 500,000 VNĐ đều có thể đáp ứng tốt cho tập luyện và thi đấu.
Lợi Ích Khi Sử Dụng Bóng Rổ Cao Su
- Giúp cải thiện kỹ năng chơi bóng, đặc biệt là khi tập luyện ngoài trời với điều kiện sân không hoàn hảo.
- Thúc đẩy sức khỏe và thể chất, đặc biệt là đối với giới trẻ và những người yêu thích thể thao.
- Dễ dàng mua sắm tại các cửa hàng thể thao hoặc trực tuyến với giá cả phải chăng.
Bóng rổ cao su là sự lựa chọn tuyệt vời cho người chơi không chuyên lẫn chuyên nghiệp. Hãy chọn cho mình một quả bóng chất lượng để trải nghiệm môn thể thao này một cách tốt nhất!

.png)
Mục Lục
Bóng Rổ Cao Su - Đặc Điểm và Ưu Điểm Nổi Bật
Các Loại Bóng Rổ Cao Su Phổ Biến Tại Việt Nam
So Sánh Bóng Rổ Cao Su và Bóng Rổ Da
Cách Chọn Mua Bóng Rổ Cao Su Phù Hợp
Giá Bán Của Bóng Rổ Cao Su Trên Thị Trường
Hướng Dẫn Bảo Quản Bóng Rổ Cao Su Để Dùng Lâu Bền
Bóng Rổ Cao Su Cho Người Mới Bắt Đầu - Cách Tập Luyện Hiệu Quả
Các Thương Hiệu Bóng Rổ Cao Su Hàng Đầu Tại Việt Nam
Mua Bóng Rổ Cao Su Ở Đâu Uy Tín Nhất?
Lợi Ích Sức Khỏe Khi Chơi Bóng Rổ Cao Su
Bóng rổ cao su là loại bóng được sản xuất từ chất liệu cao su bền bỉ, phù hợp với nhiều điều kiện sân chơi khác nhau, đặc biệt là sân ngoài trời.
Tìm hiểu về các dòng bóng rổ cao su đến từ các thương hiệu nổi tiếng như Molten, GeruStar, và Spalding.
Điểm khác biệt giữa bóng rổ cao su và bóng rổ da về giá cả, độ bền, cảm giác cầm nắm, và khả năng chơi trên sân.
Hướng dẫn chi tiết cách chọn kích cỡ bóng phù hợp cho từng độ tuổi, từ bóng rổ size 5 đến size 7.
Tổng hợp các mức giá phổ biến của bóng rổ cao su, từ các mẫu giá rẻ đến các dòng cao cấp.
Các mẹo và cách bảo quản bóng rổ cao su giúp duy trì độ nảy và độ bền trong thời gian dài.
Các bài tập cơ bản và nâng cao giúp người mới tập chơi bóng rổ cải thiện kỹ năng nhanh chóng.
Danh sách các thương hiệu bóng rổ cao su uy tín được người tiêu dùng ưa chuộng tại Việt Nam.
Hướng dẫn địa điểm mua bóng rổ cao su chính hãng từ các nhà phân phối và cửa hàng thể thao uy tín.
Những tác động tích cực của việc chơi bóng rổ cao su đến sức khỏe thể chất và tinh thần.
Bài Tập Thực Hành Toán Liên Quan Đến Bóng Rổ Cao Su
Trong phần này, chúng ta sẽ áp dụng các kiến thức toán học vào việc giải quyết các bài toán liên quan đến bóng rổ cao su, giúp nâng cao khả năng tính toán và tư duy logic.
Bài Tập 1: Tính Diện Tích Mặt Bóng Rổ
Giả sử quả bóng rổ có đường kính là 24 cm. Tính diện tích bề mặt của quả bóng.
Sử dụng công thức tính diện tích bề mặt của hình cầu:
\[
A = 4 \pi r^2
\]
Với bán kính \( r = \frac{24}{2} = 12 \) cm, ta có:
\[
A = 4 \pi (12)^2 = 4 \pi \times 144 = 576 \pi \ \text{cm}^2
\]
Bài Tập 2: Tính Thể Tích Bóng Rổ
Cho rằng quả bóng rổ có bán kính là 12 cm. Tính thể tích của quả bóng.
Sử dụng công thức tính thể tích hình cầu:
\[
V = \frac{4}{3} \pi r^3
\]
Với \( r = 12 \) cm, ta có:
\[
V = \frac{4}{3} \pi (12)^3 = \frac{4}{3} \pi \times 1728 = 2304 \pi \ \text{cm}^3
\]
Bài Tập 3: Tính Khối Lượng Bóng Rổ
Quả bóng rổ có thể tích 2304 cm³ và mật độ cao su là 0.92 g/cm³. Tính khối lượng của quả bóng.
Khối lượng được tính bằng công thức:
\[
M = \text{Thể tích} \times \text{Mật độ} = 2304 \times 0.92 = 2120.64 \ \text{g} = 2.12 \ \text{kg}
\]
Bài Tập 4: So Sánh Tốc Độ Giữa Hai Quả Bóng Rổ
Hai quả bóng rổ có khối lượng lần lượt là 600 g và 650 g. Nếu cùng một lực tác động, tính tỉ lệ tốc độ của hai quả bóng.
Sử dụng định luật bảo toàn động lượng, ta có:
\[
v_1 / v_2 = M_2 / M_1 = 650 / 600 = 1.083
\]
Vậy tỉ lệ tốc độ của quả bóng nhẹ hơn so với quả bóng nặng hơn là 1.083.
Bài Tập 5: Tính Lực Cản Không Khí Lên Bóng Rổ
Một quả bóng rổ có diện tích mặt cắt ngang là 0.045 m², di chuyển với vận tốc 10 m/s. Tính lực cản của không khí nếu hệ số cản là 0.47 và mật độ không khí là 1.225 kg/m³.
Sử dụng công thức tính lực cản:
\[
F = \frac{1}{2} C_d \rho v^2 A
\]
Thay số vào công thức:
\[
F = \frac{1}{2} \times 0.47 \times 1.225 \times (10)^2 \times 0.045 = 1.3 \ \text{N}
\]
Bài Tập 6: Tính Khoảng Cách Bay Của Bóng Rổ
Bóng rổ được ném với vận tốc ban đầu là 15 m/s ở góc 45 độ so với mặt đất. Tính khoảng cách bay của bóng.
Sử dụng công thức tính khoảng cách bay của vật ném xiên:
\[
d = \frac{v_0^2 \sin(2 \theta)}{g}
\]
Với \(v_0 = 15 \ \text{m/s}, \ \theta = 45^\circ\), ta có:
\[
d = \frac{(15)^2 \times \sin(90^\circ)}{9.81} = \frac{225}{9.81} \approx 22.93 \ \text{m}
\]
Bài Tập 7: Tính Thời Gian Bóng Rơi Xuống Đất
Bóng rổ được ném từ độ cao 2 m với vận tốc ban đầu 10 m/s. Tính thời gian bóng chạm đất.
Sử dụng công thức tính thời gian rơi:
\[
t = \frac{v_0 \sin(\theta) + \sqrt{(v_0 \sin(\theta))^2 + 2gh}}{g}
\]
Bài Tập 8: Tính Áp Suất Bên Trong Bóng Rổ
Áp suất bên trong quả bóng rổ là 0.8 atm và bán kính của bóng là 12 cm. Tính lực tác động lên mặt trong của bóng rổ.
Sử dụng công thức tính lực:
\[
F = p \times A
\]
Với \( p = 0.8 \ \text{atm} = 81000 \ \text{Pa}, A = 4 \pi r^2 \), thay vào ta có:
\[
F = 81000 \times 4 \pi (0.12)^2 \approx 14651 \ \text{N}
\]
Bài Tập 9: Tính Công Suất Khi Ném Bóng
Một người ném bóng rổ với lực là 200 N trong thời gian 0.5 giây. Tính công suất khi ném bóng.
Sử dụng công thức tính công suất:
\[
P = \frac{F \times d}{t}
\]
Bài Tập 10: Tính Động Năng Của Bóng Rổ
Quả bóng rổ có khối lượng 600 g, di chuyển với vận tốc 12 m/s. Tính động năng của bóng.
Sử dụng công thức tính động năng:
\[
E_k = \frac{1}{2} m v^2
\]
Với \( m = 0.6 \ \text{kg}, v = 12 \ \text{m/s}\), thay vào ta có:
\[
E_k = \frac{1}{2} \times 0.6 \times (12)^2 = 43.2 \ \text{J}
\]

Bài Tập 1: Tính diện tích mặt bóng rổ
Bài tập này yêu cầu bạn tính diện tích bề mặt của một quả bóng rổ có đường kính là 24 cm. Để giải quyết bài toán, chúng ta sẽ sử dụng công thức tính diện tích bề mặt của hình cầu.
Bước 1: Xác định bán kính của quả bóng
Quả bóng rổ có đường kính là 24 cm, do đó bán kính của quả bóng được tính như sau:
\[
r = \frac{24}{2} = 12 \ \text{cm}
\]
Bước 2: Sử dụng công thức tính diện tích mặt cầu
Công thức tính diện tích mặt cầu là:
\[
A = 4 \pi r^2
\]
Trong đó:
- \(A\) là diện tích mặt cầu
- \(r\) là bán kính quả bóng
- \(\pi\) là hằng số toán học xấp xỉ \(3.14159\)
Bước 3: Tính diện tích mặt bóng rổ
Thay giá trị bán kính \(r = 12 \ \text{cm}\) vào công thức, ta có:
\[
A = 4 \pi (12)^2 = 4 \pi \times 144 = 576 \pi \ \text{cm}^2
\]
Sử dụng giá trị xấp xỉ của \(\pi \approx 3.14159\), diện tích mặt bóng rổ được tính như sau:
\[
A \approx 576 \times 3.14159 = 1809.56 \ \text{cm}^2
\]
Kết luận
Vậy, diện tích bề mặt của quả bóng rổ có đường kính 24 cm là khoảng \(1809.56 \ \text{cm}^2\).
Bài Tập 2: Tính thể tích bóng rổ
Trong bài tập này, chúng ta sẽ tính thể tích của một quả bóng rổ có đường kính là 24 cm. Để tính thể tích của hình cầu, ta sẽ áp dụng công thức tính thể tích.
Bước 1: Xác định bán kính của quả bóng
Quả bóng rổ có đường kính là 24 cm, vì vậy bán kính của quả bóng là:
Bước 2: Sử dụng công thức tính thể tích hình cầu
Thể tích hình cầu được tính bằng công thức:
Trong đó:
- \(V\) là thể tích hình cầu
- \(r\) là bán kính của quả bóng
- \(\pi\) là hằng số toán học, xấp xỉ \(3.14159\)
Bước 3: Thay giá trị vào công thức
Thay bán kính \(r = 12 \ \text{cm}\) vào công thức, ta có:
Sử dụng giá trị xấp xỉ của \(\pi \approx 3.14159\), thể tích của quả bóng rổ được tính như sau:
Kết luận
Vậy, thể tích của quả bóng rổ có đường kính 24 cm là khoảng \(7238.23 \ \text{cm}^3\).

Bài Tập 3: Tính khối lượng của bóng rổ
Trong bài tập này, chúng ta sẽ tính khối lượng của một quả bóng rổ dựa trên thể tích của nó và mật độ cao su. Giả sử quả bóng rổ được làm từ cao su có mật độ nhất định.
Bước 1: Xác định các thông số cần thiết
Chúng ta đã biết rằng thể tích của quả bóng rổ được tính từ bài tập trước là:
Mật độ của cao su được giả định là \( \rho = 0.92 \ \text{g/cm}^3 \).
Bước 2: Sử dụng công thức tính khối lượng
Khối lượng của quả bóng rổ được tính bằng công thức:
Trong đó:
- \(M\) là khối lượng của quả bóng
- \(\rho\) là mật độ của cao su
- \(V\) là thể tích của quả bóng
Bước 3: Thay số liệu vào công thức
Thay các giá trị đã biết vào công thức:
Chuyển đổi khối lượng sang đơn vị kilogram:
Kết luận
Vậy, khối lượng của quả bóng rổ có thể tích 7238.23 cm³ và mật độ cao su là 0.92 g/cm³ sẽ là khoảng \( 6.67 \ \text{kg} \).
XEM THÊM:
Bài Tập 4: So sánh tốc độ bay của các loại bóng rổ
Trong môn bóng rổ, tốc độ bay của quả bóng đóng vai trò quan trọng trong việc xác định hiệu quả của các cú ném và chuyền. Tốc độ bay của bóng rổ có thể bị ảnh hưởng bởi nhiều yếu tố, bao gồm khối lượng của quả bóng, lực tác động, và cả đặc tính của vật liệu cấu tạo bóng. Dưới đây, chúng ta sẽ so sánh tốc độ bay của hai quả bóng rổ có khối lượng khác nhau khi chịu cùng một lực tác động.
Giả sử:
- Quả bóng rổ 1 có khối lượng \( M_1 = 600 \) g.
- Quả bóng rổ 2 có khối lượng \( M_2 = 650 \) g.
- Lực tác động lên cả hai quả bóng là như nhau.
Theo định luật bảo toàn động lượng, tốc độ bay của hai quả bóng có thể so sánh bằng công thức:
\[ \frac{v_1}{v_2} = \frac{M_2}{M_1} \]
Thay số vào công thức:
\[ \frac{v_1}{v_2} = \frac{650}{600} \approx 1.083 \]
Điều này có nghĩa là với cùng một lực tác động, quả bóng rổ 1 (600 g) sẽ bay nhanh hơn quả bóng rổ 2 (650 g) khoảng 8.3%. Nói cách khác, khối lượng càng nhỏ, tốc độ bay càng lớn khi lực tác động không đổi.
Việc hiểu rõ về mối quan hệ giữa khối lượng và tốc độ bay của bóng rổ không chỉ giúp cải thiện kỹ năng ném và chuyền bóng mà còn hỗ trợ trong việc lựa chọn quả bóng phù hợp với mục tiêu luyện tập và thi đấu.
Bài Tập 5: Tính lực cản của không khí lên bóng rổ
Khi quả bóng rổ di chuyển trong không khí, nó phải đối mặt với một lực cản từ môi trường xung quanh. Lực cản này phụ thuộc vào nhiều yếu tố như diện tích mặt cắt ngang của bóng, vận tốc di chuyển, mật độ không khí và hệ số cản khí động học của quả bóng.
Trong bài tập này, chúng ta sẽ tính toán lực cản của không khí lên quả bóng rổ dựa trên các thông số sau:
- Diện tích mặt cắt ngang của bóng (\(A\)): 0.045 m²
- Vận tốc di chuyển của bóng (\(v\)): 10 m/s
- Hệ số cản khí động học (\(C_d\)): 0.47
- Mật độ không khí (\(\rho\)): 1.225 kg/m³ (giá trị thông dụng ở mực nước biển)
Lực cản không khí (\(F\)) được tính bằng công thức:
Thay các giá trị vào công thức:
Thực hiện phép tính:
Vậy lực cản của không khí lên quả bóng rổ là khoảng 1.296 N.
Việc tính toán lực cản không khí giúp bạn hiểu rõ hơn về cách các yếu tố môi trường ảnh hưởng đến chuyển động của bóng rổ. Điều này không chỉ quan trọng trong việc tối ưu hóa hiệu suất trong các trận đấu, mà còn giúp bạn điều chỉnh các kỹ thuật ném bóng sao cho phù hợp nhất.

Bài Tập 6: Tính khoảng cách bay của bóng rổ
Trong bài tập này, chúng ta sẽ tính khoảng cách mà quả bóng rổ có thể bay được khi được ném với một vận tốc ban đầu nhất định và góc ném so với mặt đất. Để giải quyết bài toán này, chúng ta sẽ sử dụng công thức ném xiên trong vật lý.
Giả sử, một quả bóng rổ được ném với vận tốc ban đầu là \( v_0 = 15 \, \text{m/s} \) và góc ném so với mặt đất là \( \theta = 45^\circ \). Chúng ta cần tính khoảng cách bay xa nhất của bóng, bỏ qua lực cản của không khí.
Công thức tính khoảng cách bay xa \( d \) là:
\[
d = \frac{v_0^2 \sin(2\theta)}{g}
\]
Trong đó:
- \( v_0 \) là vận tốc ban đầu của bóng.
- \( \theta \) là góc ném so với mặt đất.
- \( g \) là gia tốc trọng trường, giá trị trung bình là \( 9.8 \, \text{m/s}^2 \).
Bây giờ, ta thay các giá trị vào công thức:
\[
d = \frac{15^2 \times \sin(2 \times 45^\circ)}{9.8}
\]
Ta có \( \sin(90^\circ) = 1 \), do đó:
\[
d = \frac{225 \times 1}{9.8} \approx 22.96 \, \text{m}
\]
Vậy, khoảng cách bay của quả bóng rổ trong điều kiện lý tưởng là khoảng 22.96 mét.
Đây là một bài tập cơ bản nhưng rất quan trọng để hiểu cách lực tác động và góc ném ảnh hưởng đến quỹ đạo bay của bóng rổ. Điều này cũng minh họa tầm quan trọng của việc lựa chọn góc ném phù hợp để đạt được khoảng cách bay tối đa trong thi đấu và luyện tập.
Bài Tập 7: Tính thời gian bay của bóng rổ
Trong bài tập này, chúng ta sẽ tính thời gian bay của quả bóng rổ khi được ném từ độ cao nhất định với một vận tốc ban đầu. Đây là bài tập thú vị giúp bạn hiểu rõ hơn về cách các yếu tố như độ cao, vận tốc và lực hấp dẫn ảnh hưởng đến quỹ đạo và thời gian bay của quả bóng.
Đề bài: Giả sử quả bóng rổ được ném từ độ cao 2 m so với mặt đất với vận tốc ban đầu là 12 m/s theo phương ngang. Hãy tính thời gian bóng rơi chạm đất.
Lời giải:
Bước 1: Xác định các thông số đã cho:
- Độ cao ban đầu, \( h_0 = 2 \, \text{m} \)
- Vận tốc ban đầu theo phương ngang, \( v_0 = 12 \, \text{m/s} \)
- Gia tốc trọng trường, \( g = 9.81 \, \text{m/s}^2 \)
Bước 2: Tính thời gian bóng rơi chạm đất:
Thời gian rơi tự do của bóng rổ chỉ phụ thuộc vào độ cao ban đầu và gia tốc trọng trường, không phụ thuộc vào vận tốc ban đầu theo phương ngang. Chúng ta sử dụng công thức sau:
\[
t = \sqrt{\frac{2h_0}{g}}
\]Thay các giá trị đã cho vào công thức:
\[
t = \sqrt{\frac{2 \times 2}{9.81}} \approx 0.64 \, \text{giây}
\]Bước 3: Kết luận:
Thời gian bay của quả bóng rổ là khoảng \( 0.64 \, \text{giây} \).
Như vậy, khi ném quả bóng rổ từ độ cao 2 m với vận tốc ban đầu 12 m/s, bóng sẽ rơi chạm đất sau khoảng 0.64 giây. Điều này minh họa rằng thời gian rơi tự do của vật không bị ảnh hưởng bởi vận tốc ngang của nó, mà chỉ phụ thuộc vào độ cao ban đầu và gia tốc trọng trường.
Bài Tập 8: Tính áp lực bên trong bóng rổ
Để tính áp lực bên trong quả bóng rổ, chúng ta cần biết áp suất bên trong quả bóng và diện tích bề mặt bên trong của nó. Giả sử áp suất bên trong quả bóng là 0.8 atm và bán kính của quả bóng là 12 cm.
Bước 1: Chuyển đổi áp suất từ đơn vị atm sang Pascal (Pa). Biết rằng 1 atm = 101325 Pa, ta có:
\[
p = 0.8 \times 101325 = 81060 \text{ Pa}
\]
Bước 2: Tính diện tích bề mặt của quả bóng rổ. Sử dụng công thức diện tích bề mặt của hình cầu:
\[
A = 4 \pi r^2
\]
với \( r = 12 \) cm = 0.12 m, ta có:
\[
A = 4 \times 3.1416 \times (0.12)^2 = 0.1809 \text{ m}^2
\]
Bước 3: Tính lực tác động lên mặt trong của bóng rổ bằng công thức:
\[
F = p \times A
\]
Thay giá trị vào công thức, ta được:
\[
F = 81060 \times 0.1809 = 14665.5 \text{ N}
\]
Vậy, lực tác động lên mặt trong của quả bóng rổ là khoảng 14665.5 Newton.
Bài Tập 9: Tính công suất khi ném bóng
Để tính toán công suất khi ném bóng rổ, chúng ta cần phải xem xét các yếu tố quan trọng như lực tác động, thời gian thực hiện ném bóng, và vận tốc của quả bóng ngay tại thời điểm vừa rời khỏi tay người ném.
-
Bước 1: Xác định lực tác động lên bóng rổ
Giả sử bạn đã biết khối lượng của quả bóng rổ (\(m\)) và vận tốc của bóng ngay tại thời điểm vừa rời tay (\(v\)). Lực tác động (\(F\)) có thể được tính toán thông qua công thức:
\[
F = m \times a
\]
trong đó, \(a\) là gia tốc của bóng rổ. -
Bước 2: Xác định thời gian ném bóng
Thời gian ném bóng (\(t\)) là khoảng thời gian từ lúc bạn bắt đầu ném cho đến khi bóng rời tay. Thời gian này có thể được đo đạc trực tiếp trong quá trình ném bóng.
-
Bước 3: Tính công suất
Công suất (\(P\)) được tính theo công thức:
\[
P = \frac{F \times d}{t}
\]
trong đó:
- \(F\) là lực tác động lên bóng rổ.
- \(d\) là khoảng cách mà lực này đã tác động trong thời gian \(t\).
- \(t\) là thời gian thực hiện ném bóng.
Ngoài ra, công suất còn có thể được tính bằng cách nhân lực tác động với vận tốc của quả bóng ngay tại thời điểm nó rời tay bạn:
\[
P = F \times v
\] -
Bước 4: Kiểm tra và điều chỉnh
Sau khi tính toán, hãy so sánh kết quả với thực tế. Nếu kết quả công suất không phù hợp với mong đợi, hãy xem xét lại các yếu tố như lực tác động hoặc vận tốc ban đầu của bóng.
Thực hành thường xuyên sẽ giúp bạn cải thiện độ chính xác trong việc ném bóng và hiểu rõ hơn về sự liên quan giữa lực tác động và công suất trong quá trình chơi bóng rổ.
Bài Tập 10: Tính động năng của bóng rổ khi ném
Trong bài tập này, chúng ta sẽ tính toán động năng của quả bóng rổ khi ném, dựa trên kiến thức về động học và năng lượng trong vật lý. Động năng là năng lượng mà một vật sở hữu do chuyển động của nó và được tính bằng công thức:
\[
E_k = \frac{1}{2} m v^2
\]
Trong đó:
- \(E_k\): Động năng (Joules, J)
- \(m\): Khối lượng của bóng rổ (kilograms, kg)
- \(v\): Vận tốc của bóng rổ khi ném (meters per second, m/s)
Để tính được động năng của quả bóng rổ, chúng ta cần biết các thông số sau:
- Khối lượng của quả bóng rổ. Thông thường, một quả bóng rổ có khối lượng khoảng 0.6 kg.
- Vận tốc của quả bóng rổ khi ném. Vận tốc này phụ thuộc vào người ném và kỹ thuật ném, nhưng thông thường có thể vào khoảng 8 m/s đến 12 m/s.
Ví dụ, nếu một quả bóng rổ có khối lượng 0.6 kg và được ném với vận tốc 10 m/s, động năng của nó sẽ được tính như sau:
\[
E_k = \frac{1}{2} \times 0.6 \, \text{kg} \times (10 \, \text{m/s})^2 = 30 \, \text{J}
\]
Vì vậy, động năng của quả bóng rổ trong trường hợp này là 30 Joules.
Trong quá trình thực hiện động tác ném bóng, việc duy trì một tư thế chuẩn xác và kiểm soát lực tay là điều rất quan trọng để tối ưu hóa vận tốc của bóng, qua đó tối đa hóa động năng và hiệu quả của cú ném.