Chủ đề đêm nay bóng đá mấy giờ: Đêm nay bóng đá mấy giờ? Hãy cùng chúng tôi cập nhật nhanh nhất lịch thi đấu các trận cầu đỉnh cao từ Ngoại Hạng Anh, La Liga, Serie A, đến Champions League và V-League. Đừng bỏ lỡ thông tin quan trọng về thời gian diễn ra các trận đấu để không bỏ qua những khoảnh khắc kịch tính nhất!
Mục lục
- Lịch Thi Đấu Bóng Đá Đêm Nay
- Mục Lục Tổng Hợp
- Dạng Bài Tập: Giải Toán Học Đặc Sắc
- Dạng Bài Tập: Lý Thuyết Vật Lý Quan Trọng
- Dạng Bài Tập: Phân Tích Ngữ Pháp Tiếng Anh
- Dạng Bài Tập: Giải Phương Trình Toán Cao Cấp
- Dạng Bài Tập: Bài Tập Tích Phân Và Ứng Dụng
- Dạng Bài Tập: Bài Tập Hình Học Không Gian
- Dạng Bài Tập: Bài Tập Vật Lý Cơ Học
- Dạng Bài Tập: Bài Tập Tiếng Anh Giao Tiếp
- Dạng Bài Tập: Giải Hệ Phương Trình Tuyến Tính
- Dạng Bài Tập: Bài Tập Số Phức Và Ứng Dụng
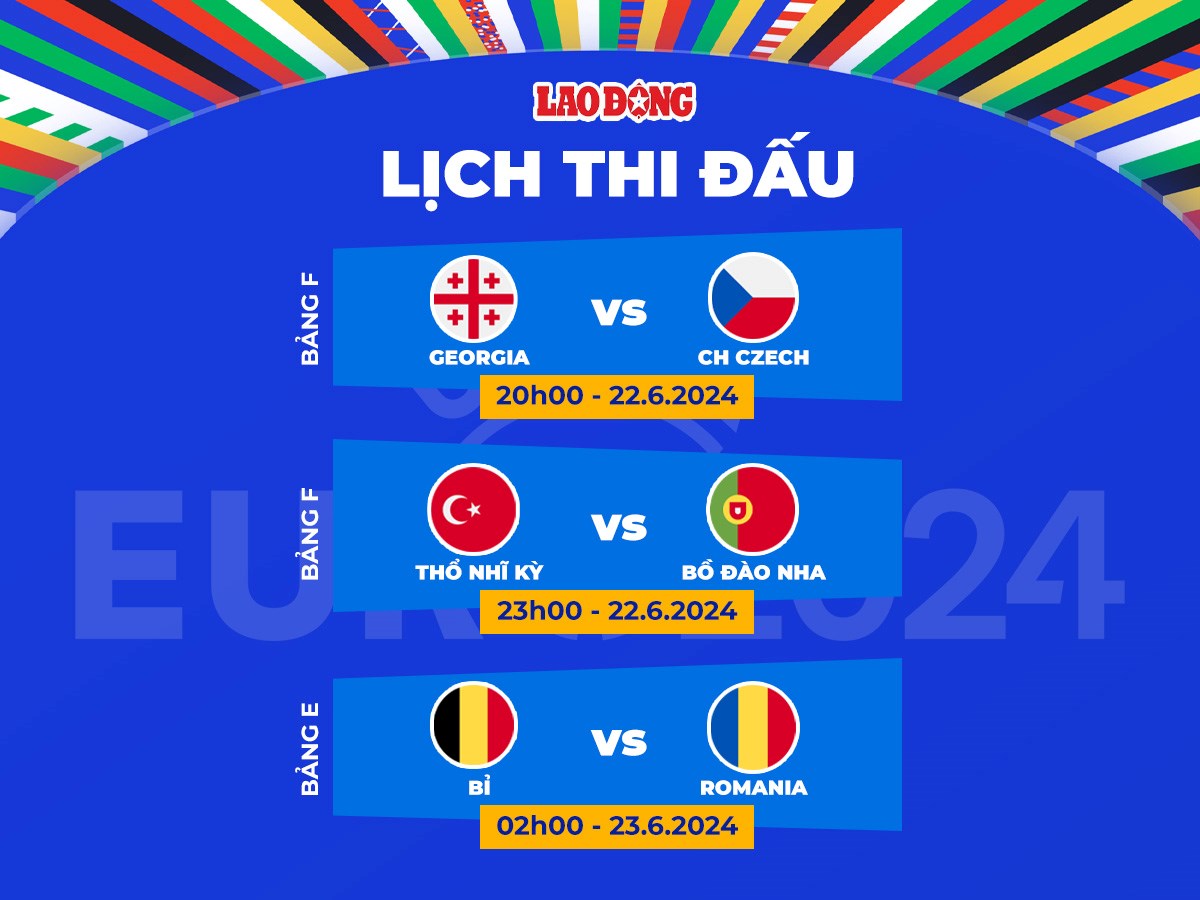
Lịch Thi Đấu Bóng Đá Đêm Nay
Dưới đây là thông tin chi tiết về lịch thi đấu bóng đá diễn ra vào đêm nay từ nhiều giải đấu khác nhau trên thế giới.
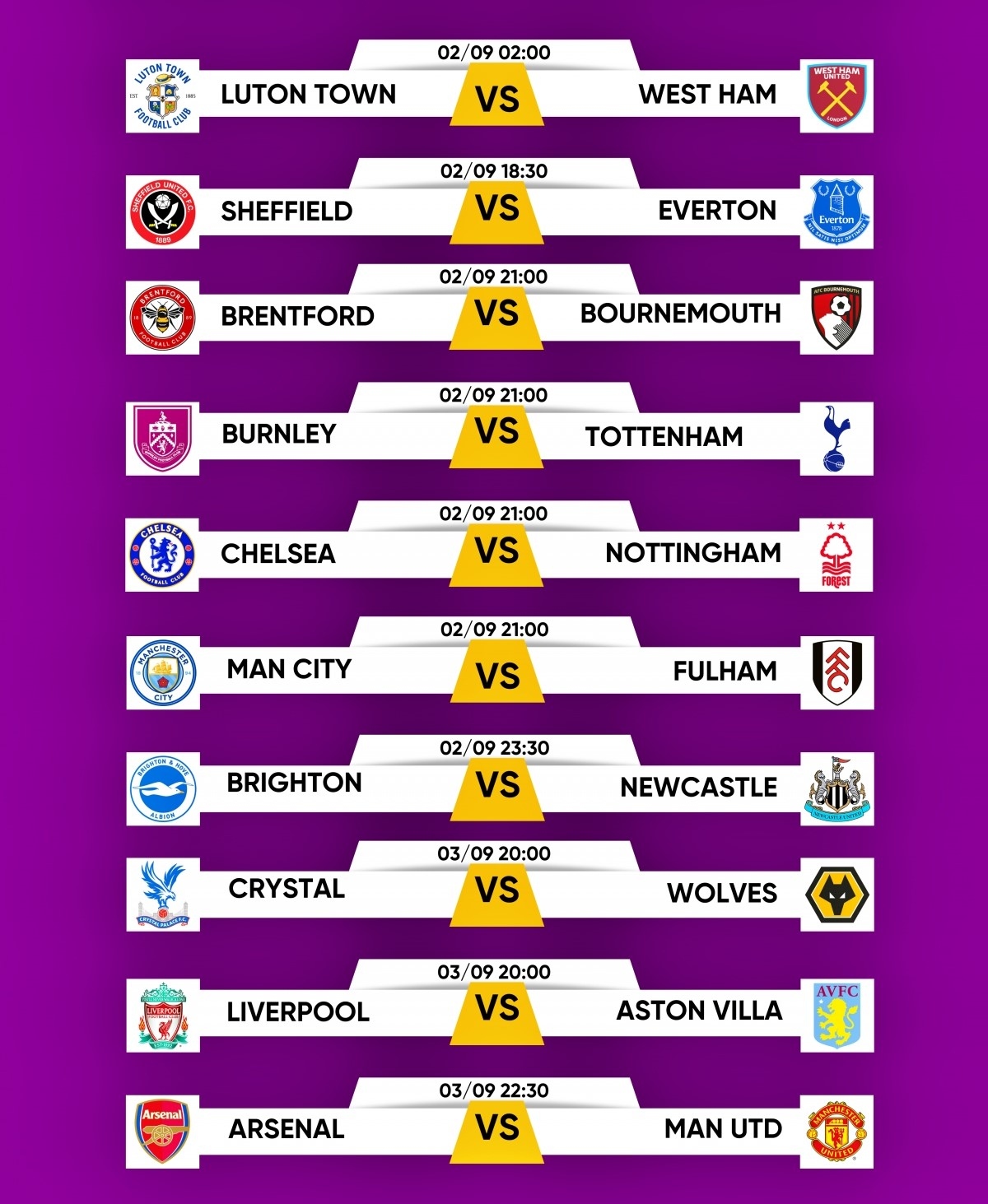
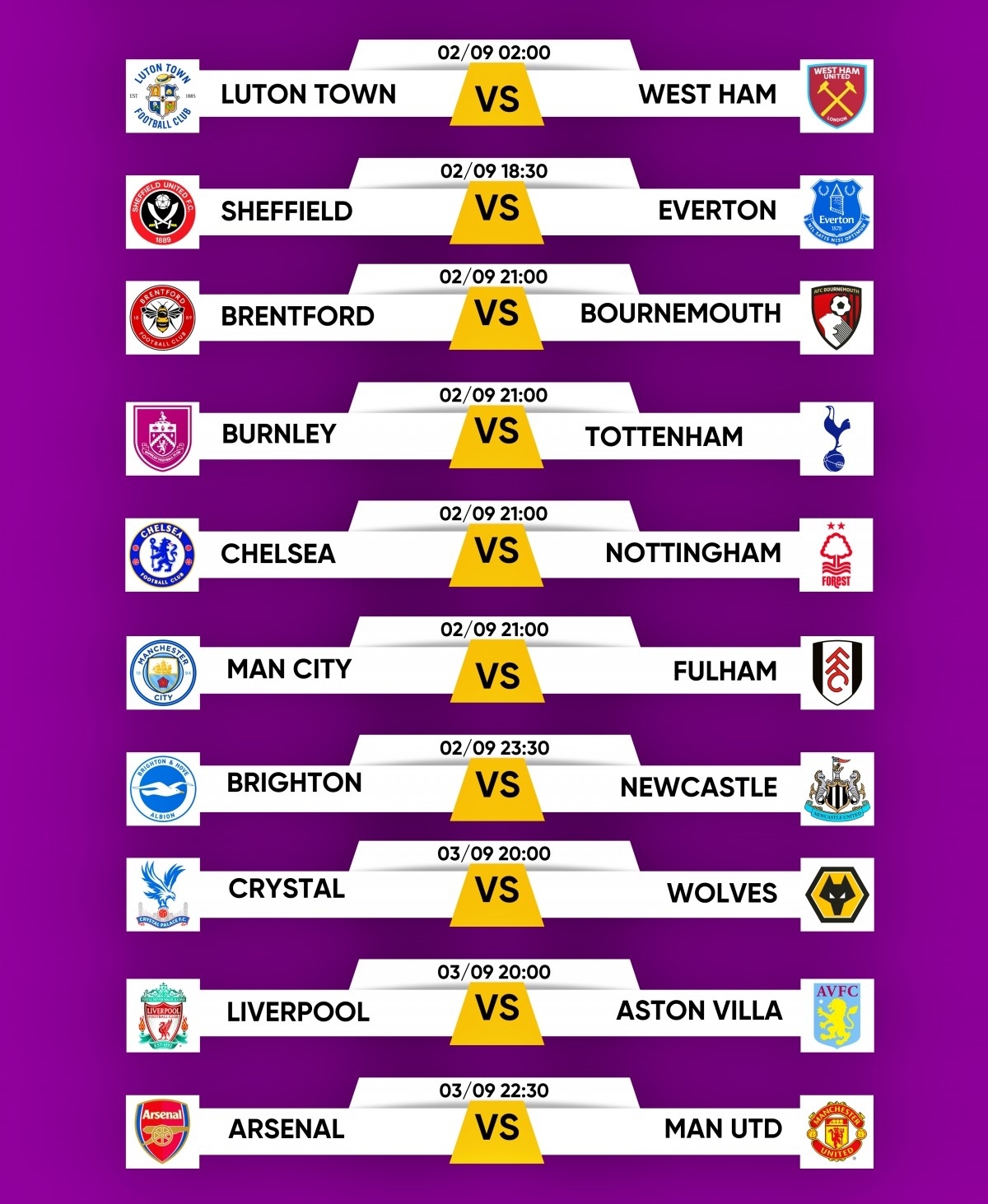
1. Ngoại Hạng Anh
- Brighton vs Manchester United: 18:30
- Manchester City vs Ipswich: 21:00
- Tottenham vs Everton: 21:00
- Aston Villa vs Arsenal: 23:30
2. Vô Địch Quốc Gia Tây Ban Nha (La Liga)
- Osasuna vs Mallorca: 22:00
- Barcelona vs Ath. Bilbao: 00:00
- Espanyol vs Real Sociedad: 02:30
3. Vô Địch Quốc Gia Ý (Serie A)
- Parma vs AC Milan: 23:30
- Inter Milan vs Lecce: 01:45
4. Vô Địch Quốc Gia Đức (Bundesliga)
- Bayern Munich vs RB Leipzig: 23:30
- Borussia Dortmund vs Hertha Berlin: 01:45
5. Champions League
Trận đấu tại vòng loại Champions League:
- Real Madrid vs PSG: 02:00
- Liverpool vs Bayern Munich: 02:00
6. Các Giải Đấu Khác
- V-League (Việt Nam): Nam Định vs Hà Nội: 19:15
- Hạng Nhất Quốc Gia: Long An vs Quảng Nam: 18:00
7. Xem Trực Tiếp
Để theo dõi các trận đấu này, bạn có thể xem trực tiếp trên các kênh truyền hình như K+SPORT 1, K+LIFE, SCTV 15 và nhiều nền tảng trực tuyến khác.
Chúc các bạn có một buổi tối thú vị cùng những trận cầu đỉnh cao!
.png)
Mục Lục Tổng Hợp
- 1. Giới Thiệu Lịch Thi Đấu Đêm Nay
- 2. Lịch Thi Đấu Ngoại Hạng Anh
- 3. Lịch Thi Đấu La Liga
- 4. Lịch Thi Đấu Serie A
- 5. Lịch Thi Đấu Bundesliga
- 6. Lịch Thi Đấu Ligue 1
- 7. Lịch Thi Đấu V-League
- 8. Các Trận Đấu Đáng Chú Ý
- 9. Kênh Truyền Hình Trực Tiếp
- 10. Cập Nhật Kết Quả Trực Tiếp
Cập nhật lịch thi đấu của các giải đấu hàng đầu như Ngoại Hạng Anh, La Liga, Serie A, và Bundesliga. Thông tin chi tiết về thời gian và đối thủ sẽ giúp bạn không bỏ lỡ bất kỳ trận cầu đỉnh cao nào.
Tìm hiểu giờ diễn ra các trận đấu hấp dẫn của Ngoại Hạng Anh đêm nay, bao gồm các đội bóng hàng đầu như Manchester United, Liverpool, Chelsea, và Arsenal.
Thông tin về thời gian và các cặp đấu đáng chú ý tại La Liga, giải đấu có sự góp mặt của Barcelona, Real Madrid và các đội bóng khác.
Cập nhật giờ thi đấu của các trận đấu ở Serie A, với sự hiện diện của AC Milan, Juventus, Inter Milan và những đội bóng mạnh khác.
Khám phá giờ thi đấu của các trận đấu thuộc Bundesliga, nơi Bayern Munich và Borussia Dortmund sẽ thi đấu.
Chi tiết giờ thi đấu của các trận đấu ở Ligue 1, giải đấu có sự góp mặt của Paris Saint-Germain và các câu lạc bộ nổi bật khác.
Cập nhật giờ thi đấu các trận đấu ở V-League, giải đấu hàng đầu Việt Nam với sự tham gia của các đội bóng mạnh như Hà Nội FC và Hoàng Anh Gia Lai.
Danh sách các trận đấu quan trọng nhất trong đêm nay mà bạn không thể bỏ lỡ, với những phân tích nhanh về từng trận đấu.
Thông tin về các kênh truyền hình trực tiếp, giúp bạn dễ dàng theo dõi các trận đấu hấp dẫn ngay tại nhà.
Cập nhật liên tục kết quả các trận đấu, bao gồm tỷ số và diễn biến chính.
Dạng Bài Tập: Giải Toán Học Đặc Sắc
Dưới đây là các bài tập toán học đặc sắc giúp bạn rèn luyện kỹ năng giải toán một cách toàn diện. Mỗi bài tập được thiết kế với độ khó tăng dần và cung cấp lời giải chi tiết để bạn có thể học hỏi và cải thiện khả năng tư duy toán học.
- Bài Tập 1: Giải phương trình bậc hai
Giải phương trình sau: \[ ax^2 + bx + c = 0 \]
- Bước 1: Tính Delta \(\Delta = b^2 - 4ac\)
- Bước 2: Xét các trường hợp \(\Delta > 0\), \(\Delta = 0\), \(\Delta < 0\) để tìm nghiệm
- Bước 3: Kết luận nghiệm của phương trình
- Bài Tập 2: Tính tích phân
Tính tích phân sau: \[ \int_0^1 x^2 \, dx \]
- Bước 1: Áp dụng công thức tính tích phân cơ bản \(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\)
- Bước 2: Tính kết quả tại các cận \([0, 1]\)
- Bước 3: Kết luận giá trị của tích phân
- Bài Tập 3: Giải hệ phương trình tuyến tính
Giải hệ phương trình sau:
\[
\begin{cases}
2x + 3y = 5 \\
4x - y = 1
\end{cases}
\]- Bước 1: Sử dụng phương pháp thế hoặc cộng đại số để tìm giá trị của \(x\) và \(y\)
- Bước 2: Kiểm tra lại nghiệm trong hệ phương trình ban đầu
- Bước 3: Kết luận nghiệm của hệ phương trình
- Bài Tập 4: Tính giới hạn
Tính giới hạn sau: \(\lim_{x \to 0} \frac{\sin x}{x}\)
- Bước 1: Áp dụng định lý giới hạn đặc biệt \(\lim_{x \to 0} \frac{\sin x}{x} = 1\)
- Bước 2: Kiểm tra các điều kiện của định lý
- Bước 3: Kết luận giá trị của giới hạn
- Bài Tập 5: Tìm đạo hàm
Tìm đạo hàm của hàm số \(f(x) = x^3 - 5x^2 + 2x - 1\)
- Bước 1: Áp dụng công thức đạo hàm cơ bản \(\frac{d}{dx}(x^n) = nx^{n-1}\)
- Bước 2: Tính đạo hàm từng hạng tử
- Bước 3: Kết luận đạo hàm của hàm số
- Bài Tập 6: Bài toán hình học không gian
Tính thể tích khối chóp có đáy là tam giác với các cạnh \(a, b, c\) và chiều cao \(h\)
- Bước 1: Áp dụng công thức tính thể tích khối chóp \(V = \frac{1}{3} \times S_{đáy} \times h\)
- Bước 2: Tính diện tích đáy tam giác \(S_{đáy}\) bằng công thức Heron
- Bước 3: Kết luận thể tích của khối chóp
- Bài Tập 7: Giải bất phương trình
Giải bất phương trình sau: \(x^2 - 4x + 3 > 0\)
- Bước 1: Tìm nghiệm của phương trình bậc hai tương ứng
- Bước 2: Xét dấu của biểu thức trong các khoảng nghiệm
- Bước 3: Kết luận tập nghiệm của bất phương trình
- Bài Tập 8: Bài toán dãy số
Tìm giới hạn của dãy số \(u_n = \frac{n^2 + 1}{2n^2 + 3}\) khi \(n \to \infty\)
- Bước 1: Rút gọn biểu thức \(u_n\) bằng cách chia cả tử và mẫu cho \(n^2\)
- Bước 2: Áp dụng định lý về giới hạn của dãy số
- Bước 3: Kết luận giới hạn của dãy số
- Bài Tập 9: Phương trình logarit
Giải phương trình: \(\log_2(x^2 - 4x + 4) = 3\)
- Bước 1: Đưa phương trình về dạng mũ \[x^2 - 4x + 4 = 8\]
- Bước 2: Giải phương trình bậc hai
- Bước 3: Kiểm tra điều kiện xác định và kết luận nghiệm
- Bài Tập 10: Phương trình lượng giác
Giải phương trình: \(\sin 2x = \cos x\)
- Bước 1: Sử dụng công thức lượng giác \(\sin 2x = 2\sin x \cos x\)
- Bước 2: Biến đổi phương trình về dạng cơ bản và tìm nghiệm
- Bước 3: Kết luận nghiệm của phương trình

Dạng Bài Tập: Lý Thuyết Vật Lý Quan Trọng
Dưới đây là các bài tập lý thuyết vật lý quan trọng, được thiết kế để giúp bạn nắm vững các khái niệm cơ bản và nâng cao trong vật lý. Mỗi bài tập đi kèm với lời giải chi tiết, giúp bạn dễ dàng hiểu và áp dụng vào các bài toán thực tế.
- Bài Tập 1: Định Luật Bảo Toàn Năng Lượng
Giải thích và áp dụng định luật bảo toàn năng lượng để giải bài toán sau:
- Một vật có khối lượng \(m = 2\) kg được thả rơi tự do từ độ cao \(h = 10\) m. Tính vận tốc của vật ngay trước khi chạm đất. Bỏ qua sức cản không khí.
- Bước 1: Áp dụng định luật bảo toàn năng lượng: \[ E_k + E_p = const \]
- Bước 2: Tính thế năng ban đầu \( E_p = mgh \)
- Bước 3: Tính động năng ngay trước khi chạm đất và tìm vận tốc \(v\).
- Bài Tập 2: Định Luật Newton Thứ Hai
Giải thích định luật Newton thứ hai và áp dụng để giải bài toán:
- Một lực \(F = 10\) N tác dụng lên một vật có khối lượng \(m = 2\) kg. Tính gia tốc của vật.
- Bước 1: Viết phương trình chuyển động dựa trên định luật Newton thứ hai: \[ F = ma \]
- Bước 2: Tính gia tốc \(a\).
- Bước 3: Giải thích ý nghĩa của kết quả.
- Bài Tập 3: Định Luật Ohm
Áp dụng định luật Ohm để giải bài toán sau:
- Một mạch điện có điện trở \(R = 5\) Ω và hiệu điện thế \(U = 10\) V. Tính cường độ dòng điện chạy qua mạch.
- Bước 1: Sử dụng định luật Ohm: \[ I = \frac{U}{R} \]
- Bước 2: Tính cường độ dòng điện \(I\).
- Bước 3: Đưa ra nhận xét về kết quả.
- Bài Tập 4: Định Luật Bảo Toàn Động Lượng
Áp dụng định luật bảo toàn động lượng để giải bài toán:
- Hai vật có khối lượng \(m_1 = 3\) kg và \(m_2 = 2\) kg va chạm đàn hồi. Vận tốc ban đầu của \(m_1\) là 4 m/s và của \(m_2\) là -2 m/s. Tính vận tốc của hai vật sau va chạm.
- Bước 1: Viết phương trình bảo toàn động lượng: \[ m_1v_1 + m_2v_2 = m_1v_1' + m_2v_2' \]
- Bước 2: Áp dụng điều kiện va chạm đàn hồi và giải hệ phương trình để tìm \(v_1'\) và \(v_2'\).
- Bài Tập 5: Nguyên Lý Bất Định Heisenberg
Giải thích và áp dụng nguyên lý bất định Heisenberg:
- Một hạt có khối lượng rất nhỏ đang di chuyển với vận tốc không xác định chính xác. Giải thích sự bất định trong vị trí và động lượng của hạt.
- Bước 1: Trình bày nguyên lý bất định Heisenberg: \[ \Delta x \cdot \Delta p \geq \frac{h}{4\pi} \]
- Bước 2: Phân tích sự liên quan giữa vị trí và động lượng của hạt.
- Bài Tập 6: Thuyết Tương Đối Hẹp của Einstein
Áp dụng thuyết tương đối hẹp để giải bài toán sau:
- Một tàu vũ trụ di chuyển với vận tốc gần bằng vận tốc ánh sáng. Tính thời gian trôi chậm đi đối với phi hành gia so với người trên Trái Đất.
- Bước 1: Sử dụng công thức giãn nở thời gian: \[ t' = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}} \]
- Bước 2: Tính thời gian giãn nở \( t' \).
- Bài Tập 7: Định Luật Coulomb
Áp dụng định luật Coulomb để giải bài toán sau:
- Hai điện tích \(q_1 = 3 \times 10^{-6}\) C và \(q_2 = 2 \times 10^{-6}\) C đặt cách nhau 0,1 m trong chân không. Tính lực tương tác giữa hai điện tích.
- Bước 1: Sử dụng định luật Coulomb: \[ F = k \frac{|q_1 q_2|}{r^2} \]
- Bước 2: Tính lực \(F\).
- Bài Tập 8: Thuyết Lượng Tử Ánh Sáng
Áp dụng thuyết lượng tử ánh sáng để giải bài toán:
- Tính năng lượng của một photon ánh sáng có bước sóng 500 nm.
- Bước 1: Sử dụng công thức tính năng lượng: \[ E = \frac{hc}{\lambda} \]
- Bước 2: Tính năng lượng \(E\) của photon.
- Bài Tập 9: Định Luật Khúc Xạ Ánh Sáng
Áp dụng định luật khúc xạ ánh sáng để giải bài toán:
- Một tia sáng truyền từ không khí vào nước với góc tới 30°. Tính góc khúc xạ trong nước. Chỉ số khúc xạ của nước là 1,33.
- Bước 1: Sử dụng định luật Snell: \[ n_1 \sin \theta_1 = n_2 \sin \theta_2 \]
- Bước 2: Tính góc khúc xạ \(\theta_2\).
- Bài Tập 10: Nguyên Lý Bảo Toàn Khối Lượng và Năng Lượng
Áp dụng nguyên lý bảo toàn khối lượng và năng lượng để giải bài toán:
- Trong một phản ứng hạt nhân, một hạt nhân U-235 phân hủy thành hai mảnh nhỏ hơn và giải phóng một lượng năng lượng \(E = 200\) MeV. Tính khối lượng bị mất trong quá trình này.
- Bước 1: Sử dụng công thức Einstein: \[ E = \Delta m \cdot c^2 \]
- Bước 2: Tính khối lượng bị mất \(\Delta m\).
Dạng Bài Tập: Phân Tích Ngữ Pháp Tiếng Anh
Dưới đây là các bài tập phân tích ngữ pháp tiếng Anh giúp bạn củng cố kiến thức và nâng cao kỹ năng ngữ pháp. Mỗi bài tập được thiết kế với lời giải chi tiết, giúp bạn hiểu rõ hơn về cấu trúc ngữ pháp và cách sử dụng chúng trong các tình huống khác nhau.
- Bài Tập 1: Phân Tích Câu Trúc Chủ Ngữ - Vị Ngữ
Xác định và phân tích cấu trúc chủ ngữ và vị ngữ trong câu sau:
- "The quick brown fox jumps over the lazy dog."
- Bước 1: Xác định chủ ngữ của câu.
- Bước 2: Xác định vị ngữ và động từ chính trong câu.
- Bước 3: Phân tích mối quan hệ giữa chủ ngữ và vị ngữ.
- Bài Tập 2: Phân Tích Các Loại Từ (Parts of Speech)
Phân loại các từ trong câu sau:
- "She quickly finished her homework before going out."
- Bước 1: Xác định động từ chính và các từ bổ nghĩa.
- Bước 2: Phân loại các từ thành danh từ, động từ, tính từ, trạng từ, liên từ, giới từ, và đại từ.
- Bước 3: Phân tích chức năng của mỗi từ trong câu.
- Bài Tập 3: Phân Tích Thì Động Từ (Verb Tenses)
Xác định thì động từ và phân tích ý nghĩa của chúng trong câu sau:
- "They have been studying for three hours."
- Bước 1: Xác định động từ chính và các thành phần thì (have, been, studying).
- Bước 2: Xác định thì của động từ (Present Perfect Continuous).
- Bước 3: Phân tích ý nghĩa của thì động từ trong ngữ cảnh.
- Bài Tập 4: Phân Tích Cấu Trúc Câu Phức (Complex Sentences)
Phân tích các mệnh đề chính và phụ trong câu sau:
- "Although it was raining, we decided to go for a walk."
- Bước 1: Xác định mệnh đề chính và mệnh đề phụ.
- Bước 2: Phân tích từ nối và chức năng của nó.
- Bước 3: Giải thích cách mệnh đề phụ ảnh hưởng đến nghĩa của mệnh đề chính.
- Bài Tập 5: Phân Tích Câu Bị Động (Passive Voice)
Chuyển câu chủ động sau sang câu bị động và phân tích sự thay đổi:
- "The chef cooked a delicious meal."
- Bước 1: Xác định tân ngữ trong câu chủ động.
- Bước 2: Chuyển tân ngữ thành chủ ngữ trong câu bị động.
- Bước 3: Phân tích cấu trúc câu bị động và so sánh với câu chủ động.
- Bài Tập 6: Phân Tích Câu Điều Kiện (Conditional Sentences)
Xác định loại câu điều kiện và phân tích cấu trúc của câu sau:
- "If I had known about the party, I would have attended."
- Bước 1: Xác định các mệnh đề điều kiện và kết quả.
- Bước 2: Xác định loại câu điều kiện (Type 3).
- Bước 3: Phân tích ý nghĩa và ngữ cảnh sử dụng câu điều kiện.
- Bài Tập 7: Phân Tích Câu Hỏi Đuôi (Tag Questions)
Phân tích cấu trúc câu hỏi đuôi và sử dụng đúng ngữ pháp:
- "She can swim, can't she?"
- Bước 1: Xác định mệnh đề chính và động từ trong câu.
- Bước 2: Xác định động từ và chủ ngữ trong câu hỏi đuôi.
- Bước 3: Giải thích ngữ pháp và ngữ nghĩa của câu hỏi đuôi.
- Bài Tập 8: Phân Tích Mệnh Đề Quan Hệ (Relative Clauses)
Xác định và phân tích mệnh đề quan hệ trong câu sau:
- "The book that you gave me was really interesting."
- Bước 1: Xác định mệnh đề chính và mệnh đề quan hệ.
- Bước 2: Phân tích chức năng của từ nối trong mệnh đề quan hệ (that).
- Bước 3: Phân tích vai trò của mệnh đề quan hệ trong câu.
- Bài Tập 9: Phân Tích Liên Từ (Conjunctions)
Phân tích chức năng của các liên từ trong câu phức sau:
- "She didn't go to the party because she was tired."
- Bước 1: Xác định mệnh đề chính và phụ.
- Bước 2: Xác định và phân tích chức năng của liên từ (because).
- Bước 3: Phân tích cách liên từ kết nối và ảnh hưởng đến nghĩa của các mệnh đề.
- Bài Tập 10: Phân Tích Sự Phối Hợp Thì (Sequence of Tenses)
Xác định và phân tích sự phối hợp thì trong câu sau:
- "He said that he had finished his homework before he went out."
- Bước 1: Xác định các động từ và thì trong từng mệnh đề.
- Bước 2: Phân tích sự phối hợp thì giữa các mệnh đề.
- Bước 3: Giải thích cách sự phối hợp thì ảnh hưởng đến nghĩa của câu.

Dạng Bài Tập: Giải Phương Trình Toán Cao Cấp
Dưới đây là các bài tập giải phương trình toán cao cấp với các dạng bài phổ biến như phương trình vi phân, phương trình bậc cao, và phương trình đại số. Các bài tập được thiết kế để giúp bạn củng cố và nâng cao kỹ năng giải phương trình, với các bước giải chi tiết để bạn dễ dàng theo dõi.
- Bài Tập 1: Giải Phương Trình Vi Phân Bậc Nhất
Giải phương trình vi phân bậc nhất sau:
- \(\frac{dy}{dx} + 3y = e^{2x}\)
- Bước 1: Xác định hàm số tích phân.
- Bước 2: Tìm nghiệm tổng quát của phương trình.
- Bước 3: Áp dụng điều kiện ban đầu để tìm nghiệm cụ thể (nếu có).
- Bài Tập 2: Giải Phương Trình Đạo Hàm Riêng
Giải phương trình đạo hàm riêng sau:
- \(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0\) (Phương trình Laplace)
- Bước 1: Xác định điều kiện biên và phương pháp giải.
- Bước 2: Sử dụng phương pháp phân tách biến để giải phương trình.
- Bước 3: Tìm nghiệm tổng quát và áp dụng điều kiện biên.
- Bài Tập 3: Giải Phương Trình Đại Số Bậc Bốn
Giải phương trình đại số bậc bốn sau:
- \(x^4 - 5x^2 + 6 = 0\)
- Bước 1: Sử dụng phương pháp đặt ẩn phụ để đưa phương trình về dạng bậc hai.
- Bước 2: Giải phương trình bậc hai và tìm nghiệm của phương trình bậc bốn ban đầu.
- Bài Tập 4: Giải Phương Trình Ma Trận
Giải phương trình ma trận sau:
- \(\mathbf{AX} = \mathbf{B}\), với \(\mathbf{A}\) là ma trận \(3x3\) và \(\mathbf{B}\) là vector cột.
- Bước 1: Tìm ma trận nghịch đảo của \(\mathbf{A}\) (nếu có).
- Bước 2: Nhân ma trận nghịch đảo với \(\mathbf{B}\) để tìm vector nghiệm \(\mathbf{X}\).
- Bài Tập 5: Giải Phương Trình Đặc Trưng Của Hệ Phương Trình Tuyến Tính
Giải phương trình đặc trưng của hệ phương trình tuyến tính:
- Tìm các giá trị riêng (eigenvalues) của ma trận hệ số.
- Bước 1: Tìm định thức của ma trận hệ số trừ đi ma trận đơn vị nhân với biến \(\lambda\).
- Bước 2: Giải phương trình đa thức đặc trưng để tìm các giá trị riêng.
- Bước 3: Tìm vector riêng tương ứng với từng giá trị riêng.
- Bài Tập 6: Giải Phương Trình Đạo Hàm Toàn Phần
Giải phương trình đạo hàm toàn phần:
- \(\frac{\partial z}{\partial x} + x \frac{\partial z}{\partial y} = 0\)
- Bước 1: Sử dụng phương pháp đặc biệt (ví dụ: phương pháp biến phân) để giải phương trình.
- Bước 2: Tìm nghiệm tổng quát và phân tích điều kiện ban đầu (nếu có).
- Bài Tập 7: Giải Phương Trình Vi Phân Bậc Hai Tuyến Tính
Giải phương trình vi phân bậc hai sau:
- \(y'' - 4y' + 4y = 0\)
- Bước 1: Xác định phương trình đặc trưng liên quan đến phương trình vi phân.
- Bước 2: Tìm nghiệm của phương trình đặc trưng và từ đó tìm nghiệm của phương trình vi phân.
- Bài Tập 8: Giải Phương Trình Euler-Cauchy
Giải phương trình Euler-Cauchy sau:
- \(x^2 y'' - 3x y' + 4y = 0\)
- Bước 1: Đặt \(y = x^m\) và tìm phương trình bậc hai cho \(m\).
- Bước 2: Giải phương trình cho \(m\) và tìm nghiệm tổng quát.
- Bài Tập 9: Giải Phương Trình Đạo Hàm Riêng Phi Tuyến
Giải phương trình đạo hàm riêng phi tuyến sau:
- \(\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0\)
- Bước 1: Sử dụng phương pháp đặc biệt (ví dụ: phương pháp tuyến tính hóa) để giải.
- Bước 2: Tìm nghiệm tổng quát và phân tích điều kiện ban đầu.
- Bài Tập 10: Giải Phương Trình Schrodinger
Giải phương trình Schrodinger cho hạt trong hộp tiềm năng:
- \(-\frac{\hbar^2}{2m} \frac{\partial^2 \psi}{\partial x^2} + V(x)\psi = E\psi\)
- Bước 1: Giải phương trình trong vùng không có thế (V(x) = 0).
- Bước 2: Áp dụng điều kiện biên để tìm các nghiệm cụ thể.
XEM THÊM:
Dạng Bài Tập: Bài Tập Tích Phân Và Ứng Dụng
Tích phân là một khái niệm quan trọng trong giải tích, thường được áp dụng vào nhiều lĩnh vực như vật lý, kinh tế, và kỹ thuật. Dưới đây là một số bài tập liên quan đến tích phân và ứng dụng của nó.
1. Tính Tích Phân Cơ Bản
Hãy tính các tích phân sau:
- \(\int_0^1 x^2 \, dx\)
- \(\int_0^\pi \sin(x) \, dx\)
- \(\int_{-1}^1 e^x \, dx\)
2. Ứng Dụng Tích Phân Tính Diện Tích Hình Phẳng
Tích phân có thể được sử dụng để tính diện tích của các hình phẳng. Hãy tính diện tích vùng giới hạn bởi các đường cong sau:
- Đường cong \(y = x^2\) và trục hoành từ \(x = 0\) đến \(x = 2\).
- Đường cong \(y = \sin(x)\) và trục hoành từ \(x = 0\) đến \(x = \pi\).
3. Ứng Dụng Tích Phân Trong Vật Lý
Tích phân thường được sử dụng trong vật lý để tính toán công, năng lượng, và động lượng. Giả sử một vật chuyển động với vận tốc \(v(t) = 3t^2\), hãy tính quãng đường mà vật đi được từ \(t = 0\) đến \(t = 2\).
Giải:
Quãng đường đi được là tích phân của vận tốc theo thời gian:
Tính kết quả:
Vậy quãng đường đi được là 8 đơn vị.
4. Bài Tập Thực Hành Nâng Cao
Thử thách bản thân với các bài tập tích phân khó hơn:
- \(\int_0^1 \frac{1}{1+x^2} \, dx\)
- \(\int_1^e \ln(x) \, dx\)
- \(\int_0^\infty e^{-x^2} \, dx\) (tích phân Gauss)
Hãy thực hành và ứng dụng tích phân để làm chủ kiến thức và phát triển kỹ năng giải toán của bạn!

Dạng Bài Tập: Bài Tập Hình Học Không Gian
Bài tập hình học không gian thường yêu cầu kiến thức về các khái niệm cơ bản như mặt phẳng, đường thẳng, hình khối và góc trong không gian ba chiều. Để giải quyết những bài toán này, cần áp dụng các công thức tính toán diện tích, thể tích và mối quan hệ giữa các phần tử trong không gian. Dưới đây là một số bài tập mẫu kèm theo hướng dẫn giải chi tiết.
-
Bài tập 1: Tính thể tích của hình chóp
Cho hình chóp tam giác có đáy là tam giác đều cạnh \(a\), chiều cao \(h\). Tính thể tích của hình chóp.
Hướng dẫn giải:
- Diện tích đáy \(S\) của tam giác đều cạnh \(a\) là: \[ S = \frac{a^2 \cdot \sqrt{3}}{4} \]
- Thể tích \(V\) của hình chóp được tính bằng công thức: \[ V = \frac{1}{3} \cdot S \cdot h \]
- Thay số vào công thức để tính ra kết quả cuối cùng.
-
Bài tập 2: Tính diện tích xung quanh của hình nón
Cho hình nón có bán kính đáy là \(r\) và chiều cao là \(h\). Tính diện tích xung quanh của hình nón.
Hướng dẫn giải:
- Đường sinh \(l\) của hình nón được tính bằng: \[ l = \sqrt{r^2 + h^2} \]
- Diện tích xung quanh của hình nón là: \[ S_{xq} = \pi \cdot r \cdot l \]
- Thay số vào công thức để tính diện tích xung quanh.
-
Bài tập 3: Tính thể tích của hình cầu
Cho hình cầu có bán kính \(r\). Tính thể tích của hình cầu.
Hướng dẫn giải:
- Thể tích \(V\) của hình cầu được tính bằng công thức: \[ V = \frac{4}{3} \cdot \pi \cdot r^3 \]
- Thay số vào công thức để tính thể tích.
Những bài tập trên giúp củng cố kiến thức về hình học không gian và khả năng áp dụng công thức vào thực tiễn. Hãy thực hành thường xuyên để nâng cao kỹ năng giải toán của bạn.

Dạng Bài Tập: Bài Tập Vật Lý Cơ Học
Trong phần này, chúng ta sẽ cùng nhau ôn luyện các bài tập liên quan đến Vật Lý Cơ Học, tập trung vào các chủ đề cơ bản như chuyển động, lực, và năng lượng. Các dạng bài tập được thiết kế để giúp học sinh củng cố kiến thức và phát triển kỹ năng giải quyết vấn đề. Dưới đây là các bài tập mẫu:
-
Bài tập 1: Chuyển động thẳng đều
Một xe ô tô di chuyển thẳng đều với vận tốc 60 km/h. Tính quãng đường mà xe đi được trong 2 giờ.
Lời giải: Sử dụng công thức tính quãng đường \( S = v \times t \).
Quãng đường \( S = 60 \, \text{km/h} \times 2 \, \text{h} = 120 \, \text{km} \).
-
Bài tập 2: Chuyển động thẳng biến đổi đều
Một xe máy bắt đầu chuyển động từ trạng thái nghỉ với gia tốc \( a = 2 \, \text{m/s}^2 \). Tính vận tốc của xe sau 5 giây và quãng đường mà xe đi được trong thời gian đó.
Lời giải: Sử dụng công thức tính vận tốc \( v = a \times t \) và quãng đường \( S = \frac{1}{2} a t^2 \).
Vận tốc \( v = 2 \, \text{m/s}^2 \times 5 \, \text{s} = 10 \, \text{m/s} \).
Quãng đường \( S = \frac{1}{2} \times 2 \, \text{m/s}^2 \times (5 \, \text{s})^2 = 25 \, \text{m} \).
-
Bài tập 3: Định luật II Newton
Một vật có khối lượng 5 kg chịu tác dụng của lực \( F = 15 \, \text{N} \). Tính gia tốc của vật.
Lời giải: Sử dụng công thức định luật II Newton \( F = m \times a \).
Gia tốc \( a = \frac{F}{m} = \frac{15 \, \text{N}}{5 \, \text{kg}} = 3 \, \text{m/s}^2 \).
-
Bài tập 4: Công và năng lượng
Một vật có khối lượng 10 kg được kéo lên với lực kéo 100 N trên quãng đường 5 m. Tính công của lực kéo.
Lời giải: Sử dụng công thức tính công \( W = F \times S \times \cos(\theta) \), với \( \theta = 0^\circ \).
Công \( W = 100 \, \text{N} \times 5 \, \text{m} \times \cos(0^\circ) = 500 \, \text{J} \).
Các bài tập này sẽ giúp các bạn nắm vững các khái niệm cơ bản của vật lý cơ học, bao gồm chuyển động, lực, và năng lượng, từ đó phát triển khả năng tư duy và giải quyết các bài toán phức tạp hơn.
Dạng Bài Tập: Bài Tập Tiếng Anh Giao Tiếp
Trong phần này, chúng ta sẽ tập trung vào các bài tập tiếng Anh giao tiếp, giúp bạn nâng cao khả năng sử dụng ngôn ngữ trong các tình huống thực tế. Các bài tập được thiết kế đa dạng và phù hợp với nhiều cấp độ khác nhau, từ cơ bản đến nâng cao. Hãy luyện tập hàng ngày để cải thiện kỹ năng của mình!
Bài tập 1: Tình huống tại sân bay
- Hoàn thành đoạn hội thoại giữa một hành khách và nhân viên sân bay:
- Passenger: "Excuse me, where is the check-in counter for flight VN123?"
- Staff: "The check-in counter is over there, next to Gate 5."
- Passenger: "Thank you! What time does the boarding start?"
- Staff: "Boarding starts at 6:30 PM."
Bài tập 2: Đặt câu hỏi và trả lời trong nhà hàng
- Tạo các câu hỏi thích hợp cho các tình huống giao tiếp tại nhà hàng và trả lời chúng:
- Khách hàng hỏi về thực đơn hôm nay.
- Nhân viên trả lời về món ăn đặc biệt.
Bài tập 3: Giao tiếp tại cửa hàng mua sắm
- Đóng vai người mua hàng và nhân viên bán hàng, thực hành các mẫu câu sau:
- Customer: "Do you have this shirt in a smaller size?"
- Staff: "Yes, let me check for you."
Hãy luyện tập các tình huống giao tiếp này thường xuyên để cải thiện khả năng nói tiếng Anh của bạn. Giao tiếp tự tin, lưu loát sẽ giúp bạn thành công trong học tập và công việc.

Dạng Bài Tập: Giải Hệ Phương Trình Tuyến Tính
Trong phần này, chúng ta sẽ cùng tìm hiểu cách giải hệ phương trình tuyến tính, một trong những kiến thức quan trọng trong Toán học đại cương. Bài tập này sẽ bao gồm việc áp dụng các phương pháp giải hệ phương trình tuyến tính như phương pháp cộng đại số, phương pháp thế và phương pháp ma trận.
Ví dụ 1: Giải hệ phương trình tuyến tính đơn giản sau:
- Bước 1: Sử dụng phương pháp thế. Từ phương trình thứ hai, ta có: \[ y = 4x - 6 \]
- Bước 2: Thế giá trị của \(y\) vào phương trình thứ nhất: \[ 2x + 3(4x - 6) = 5 \] Giải phương trình trên, ta có: \[ 2x + 12x - 18 = 5 \quad \Rightarrow \quad 14x = 23 \quad \Rightarrow \quad x = \frac{23}{14} \]
- Bước 3: Thay giá trị của \(x\) vào phương trình đã thế: \[ y = 4\left(\frac{23}{14}\right) - 6 = \frac{92}{14} - 6 = \frac{92}{14} - \frac{84}{14} = \frac{8}{14} = \frac{4}{7} \]
- Vậy, nghiệm của hệ phương trình là: \[ x = \frac{23}{14}, \quad y = \frac{4}{7} \]
Ví dụ 2: Sử dụng phương pháp ma trận để giải hệ phương trình sau:
- Bước 1: Viết hệ phương trình dưới dạng ma trận: \[ A = \begin{pmatrix} 1 & 1 & 1 \\ 2 & -1 & 3 \\ 3 & 4 & 2 \end{pmatrix}, \quad \mathbf{b} = \begin{pmatrix} 6 \\ 14 \\ 18 \end{pmatrix} \]
- Bước 2: Tính nghịch đảo của ma trận \(A\), nếu có, và giải phương trình \(\mathbf{x} = A^{-1} \mathbf{b}\).
- Bước 3: Tìm ra nghiệm của hệ phương trình sau khi tính toán.
Những phương pháp này giúp giải quyết hiệu quả các bài toán hệ phương trình tuyến tính từ đơn giản đến phức tạp.
Dạng Bài Tập: Bài Tập Số Phức Và Ứng Dụng
Số phức là một khái niệm cơ bản trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực như điện tử, cơ học lượng tử, và lý thuyết điều khiển. Dưới đây là một số dạng bài tập về số phức và cách áp dụng chúng trong thực tế.
-
Bài tập 1: Tính tổng và hiệu của hai số phức.
Cho hai số phức \( z_1 = 3 + 4i \) và \( z_2 = 1 - 2i \). Tính:
- Tổng: \( z_1 + z_2 \)
- Hiệu: \( z_1 - z_2 \)
Hướng dẫn: Sử dụng tính chất cộng và trừ các phần thực và phần ảo của số phức.
-
Bài tập 2: Tính tích và thương của hai số phức.
Cho hai số phức \( z_1 = 2 + 3i \) và \( z_2 = 4 - i \). Tính:
- Tích: \( z_1 \times z_2 \)
- Thương: \( \frac{z_1}{z_2} \)
Hướng dẫn: Sử dụng công thức nhân và chia số phức, chú ý đến việc nhân liên hợp khi tính thương.
-
Bài tập 3: Tìm mô-đun và số liên hợp của số phức.
Cho số phức \( z = 5 + 12i \). Tìm:
- Mô-đun của \( z \): \( |z| \)
- Số liên hợp của \( z \): \( \overline{z} \)
Hướng dẫn: Mô-đun của số phức được tính bằng công thức \( |z| = \sqrt{x^2 + y^2} \), trong đó \( z = x + yi \).
-
Bài tập 4: Ứng dụng của số phức trong điện xoay chiều.
Trong mạch điện xoay chiều, điện áp và dòng điện thường được biểu diễn dưới dạng số phức. Cho biết một điện áp \( V = 220\cos(100\pi t) \) được biểu diễn dưới dạng số phức là \( V = 220e^{i100\pi t} \). Tính dòng điện nếu trở kháng của mạch là \( Z = 10 + 5i \) ohm.
Hướng dẫn: Sử dụng định luật Ohm dưới dạng số phức: \( I = \frac{V}{Z} \).
Qua các bài tập trên, học sinh có thể hiểu rõ hơn về cách làm việc với số phức cũng như những ứng dụng thực tiễn của chúng trong các lĩnh vực kỹ thuật và khoa học.