Chủ đề lịch thi đấu bóng đá ngoại hạng anh vòng 6: Lịch thi đấu bóng đá Ngoại hạng Anh vòng 6 đang được người hâm mộ háo hức chờ đợi. Bài viết này cung cấp thông tin chi tiết về các trận đấu, thời gian, địa điểm, và nhận định chuyên sâu. Hãy cùng theo dõi để không bỏ lỡ bất kỳ diễn biến nào của vòng đấu kịch tính này!
Mục lục
- Lịch Thi Đấu Bóng Đá Ngoại Hạng Anh Vòng 6
- Tổng Quan Về Lịch Thi Đấu Vòng 6
- Bài Tập Toán: Giải Phương Trình Bậc Hai
- Bài Tập Toán: Tính Đạo Hàm
- Bài Tập Toán: Tìm Giá Trị Cực Đại, Cực Tiểu
- Bài Tập Toán: Tích Phân Bất Định
- Bài Tập Toán: Giải Hệ Phương Trình Tuyến Tính
- Bài Tập Toán: Hình Học Không Gian
- Bài Tập Toán: Tính Diện Tích Hình Phẳng
- Bài Tập Toán: Lý Thuyết Tập Hợp
- Bài Tập Toán: Xác Suất Thống Kê
- Bài Tập Toán: Số Phức
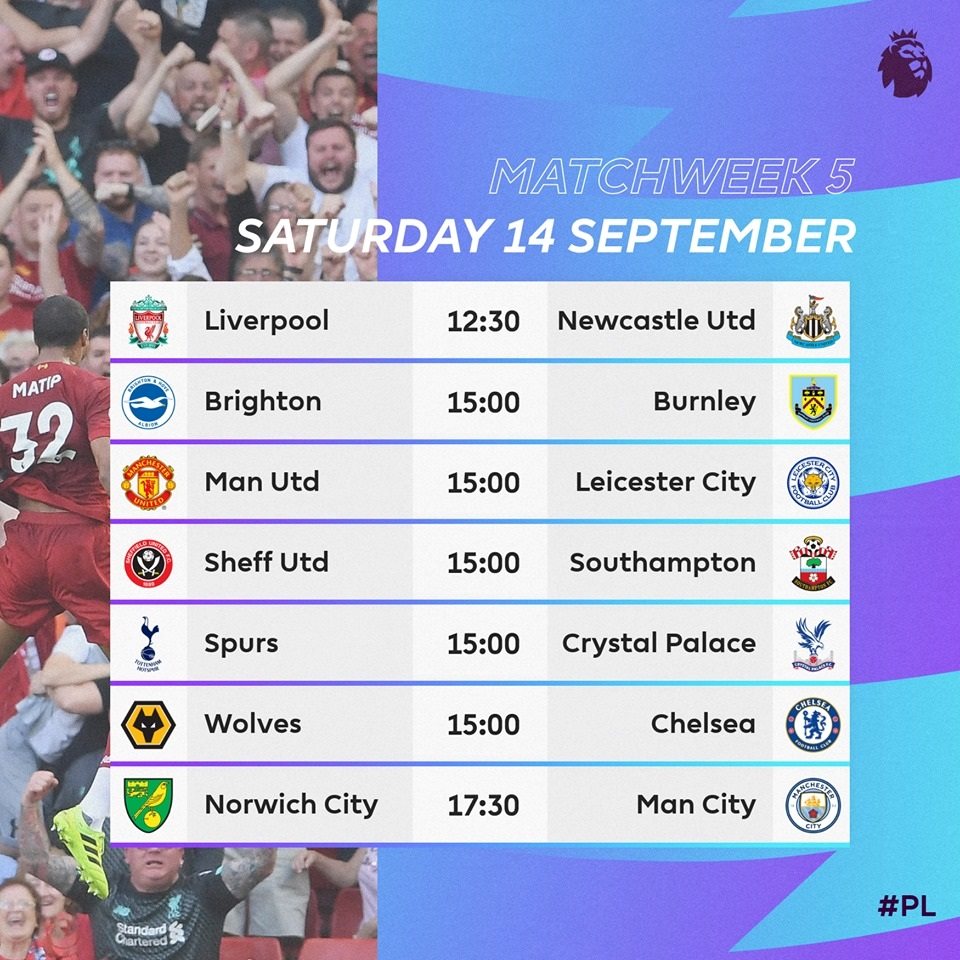
Lịch Thi Đấu Bóng Đá Ngoại Hạng Anh Vòng 6
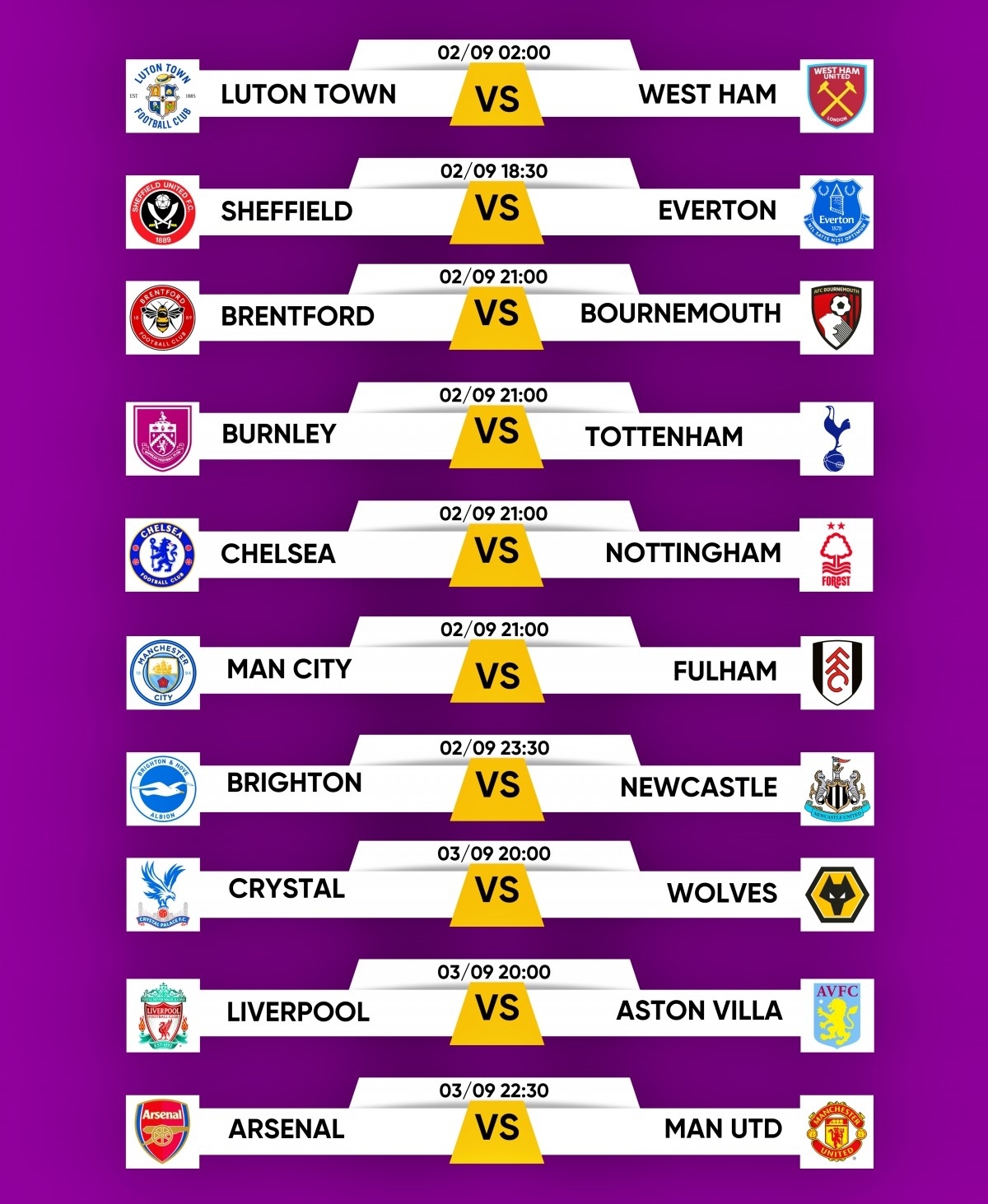
Dưới đây là thông tin chi tiết về lịch thi đấu của vòng 6 giải Ngoại hạng Anh, với những trận đấu hấp dẫn được mong đợi từ người hâm mộ.
Danh Sách Các Trận Đấu
Thời Gian Và Địa Điểm
| Trận đấu | Thời gian | Địa điểm |
|---|---|---|
| Manchester United vs Liverpool | 19:00, 23/08/2024 | Old Trafford |
| Chelsea vs Arsenal | 21:30, 23/08/2024 | Stamford Bridge |
| Manchester City vs Tottenham Hotspur | 23:00, 23/08/2024 | Etihad Stadium |
| Leicester City vs West Ham United | 01:30, 24/08/2024 | King Power Stadium |
| Everton vs Leeds United | 19:00, 24/08/2024 | Goodison Park |
| Wolves vs Aston Villa | 21:30, 24/08/2024 | Molineux Stadium |
| Southampton vs Brighton & Hove Albion | 23:00, 24/08/2024 | St. Mary's Stadium |
| Crystal Palace vs Newcastle United | 01:30, 25/08/2024 | Selhurst Park |
| Burnley vs Brentford | 19:00, 25/08/2024 | Turf Moor |
| Norwich City vs Watford | 21:30, 25/08/2024 | Carrow Road |
Dự Đoán Kết Quả
Người hâm mộ có thể kỳ vọng vào những cuộc đối đầu đầy kịch tính và những bàn thắng đẹp mắt tại vòng đấu này. Các đội bóng lớn như Manchester United, Liverpool, Chelsea và Arsenal đều đang ở trong phong độ cao, hứa hẹn sẽ mang đến những trận đấu đáng nhớ.
Các trận đấu tại vòng 6 sẽ diễn ra trên các sân vận động nổi tiếng, tạo điều kiện cho người hâm mộ theo dõi trực tiếp hoặc qua truyền hình. Hãy đón xem và cổ vũ cho đội bóng yêu thích của bạn!

.png)
Tổng Quan Về Lịch Thi Đấu Vòng 6
Vòng 6 của giải Ngoại hạng Anh hứa hẹn mang đến những trận cầu hấp dẫn với sự tham gia của các đội bóng hàng đầu. Đây là thời điểm mà mỗi trận đấu đều có thể ảnh hưởng lớn đến thứ hạng trên bảng xếp hạng. Dưới đây là tổng quan về các trận đấu trong vòng 6:
- Manchester United vs Liverpool: Trận đấu kinh điển giữa hai kỳ phùng địch thủ. Sự căng thẳng và kịch tính luôn là điểm nhấn mỗi khi hai đội gặp nhau.
- Chelsea vs Arsenal: Cuộc đối đầu giữa hai đội bóng thành London luôn là tâm điểm chú ý, với nhiều yếu tố bất ngờ và những khoảnh khắc thăng hoa.
- Manchester City vs Tottenham Hotspur: Trận đấu giữa hai đội bóng có lối chơi tấn công mạnh mẽ, hứa hẹn nhiều bàn thắng đẹp mắt.
- Leicester City vs West Ham United: Cả hai đội đều đang có phong độ cao và trận đấu này có thể là cuộc chiến giành suất dự cúp châu Âu.
- Everton vs Leeds United: Cuộc đối đầu giữa hai đội bóng có lịch sử lâu đời và phong cách chơi cống hiến.
- Wolves vs Aston Villa: Trận derby vùng Midlands luôn mang đến sự gay cấn và quyết liệt.
- Southampton vs Brighton & Hove Albion: Cả hai đội đều đang tìm kiếm điểm số quan trọng để củng cố vị trí của mình trên bảng xếp hạng.
- Crystal Palace vs Newcastle United: Trận đấu giữa hai đội bóng đang nỗ lực để thoát khỏi khu vực nguy hiểm.
- Burnley vs Brentford: Cuộc chạm trán giữa hai đội bóng có lối chơi phòng ngự kín kẽ, hứa hẹn một trận đấu chặt chẽ và chiến thuật.
- Norwich City vs Watford: Trận đấu quan trọng cho cả hai đội trong cuộc đua trụ hạng, không đội nào muốn bỏ lỡ cơ hội giành 3 điểm.
Với những trận đấu hấp dẫn như vậy, vòng 6 của giải Ngoại hạng Anh chắc chắn sẽ mang đến cho người hâm mộ nhiều cảm xúc và kịch tính. Đây là thời điểm mà các đội bóng lớn cần khẳng định sức mạnh, trong khi các đội bóng nhỏ hơn cần tận dụng cơ hội để cải thiện vị trí của mình.
Bài Tập Toán: Giải Phương Trình Bậc Hai
Phương trình bậc hai có dạng tổng quát:
Với \(a\), \(b\), và \(c\) là các hệ số thực, \(a \neq 0\). Để giải phương trình bậc hai, chúng ta có thể sử dụng công thức nghiệm:
Trong đó:
- \(b^2 - 4ac\) là delta (\(\Delta\)), được gọi là biệt thức của phương trình.
- Khi \(\Delta > 0\): Phương trình có hai nghiệm phân biệt.
- Khi \(\Delta = 0\): Phương trình có một nghiệm kép.
- Khi \(\Delta < 0\): Phương trình vô nghiệm trong tập số thực.
Ví dụ: Giải phương trình bậc hai sau:
Bước 1: Xác định các hệ số \(a = 2\), \(b = -4\), \(c = -6\).
Bước 2: Tính \(\Delta\):
Bước 3: Tính các nghiệm theo công thức:
Vậy phương trình có hai nghiệm là \(x_1 = 3\) và \(x_2 = -1\).

Bài Tập Toán: Tính Đạo Hàm
Đạo hàm của một hàm số tại một điểm thể hiện tốc độ thay đổi của hàm số tại điểm đó. Trong phần này, chúng ta sẽ xem xét cách tính đạo hàm của một số hàm cơ bản.
Ví dụ 1: Tính đạo hàm của hàm số \(f(x) = 3x^2 + 5x - 7\).
Bước 1: Xác định đạo hàm của từng hạng tử:
- \(\frac{d}{dx}(3x^2) = 6x\)
- \(\frac{d}{dx}(5x) = 5\)
- \(\frac{d}{dx}(-7) = 0\)
Bước 2: Tổng hợp các kết quả để có đạo hàm của hàm số:
Ví dụ 2: Tính đạo hàm của hàm số \(g(x) = \sin(x) + \cos(x)\).
Bước 1: Xác định đạo hàm của từng hạng tử:
- \(\frac{d}{dx}(\sin(x)) = \cos(x)\)
- \(\frac{d}{dx}(\cos(x)) = -\sin(x)\)
Bước 2: Tổng hợp các kết quả để có đạo hàm của hàm số:
Ví dụ 3: Tính đạo hàm của hàm số \(h(x) = e^{2x}\).
Bước 1: Sử dụng quy tắc chuỗi, ta có:
Như vậy, với những bước đơn giản, chúng ta đã tính được đạo hàm của các hàm số cơ bản. Đạo hàm là một công cụ mạnh mẽ trong toán học, được sử dụng rộng rãi trong các bài toán tối ưu hóa và nghiên cứu sự biến thiên của hàm số.

Bài Tập Toán: Tìm Giá Trị Cực Đại, Cực Tiểu
Trong toán học, việc tìm giá trị cực đại và cực tiểu của một hàm số là một trong những ứng dụng quan trọng của đạo hàm. Giá trị cực đại là giá trị lớn nhất của hàm số trong một khoảng, còn giá trị cực tiểu là giá trị nhỏ nhất. Dưới đây là quy trình tìm giá trị cực đại, cực tiểu của một hàm số.
Ví dụ: Tìm giá trị cực đại, cực tiểu của hàm số \(f(x) = -2x^3 + 3x^2 + 36x + 1\).
Bước 1: Tính đạo hàm bậc nhất của hàm số:
Bước 2: Tìm các điểm tới hạn bằng cách giải phương trình \(f'(x) = 0\):
Giải phương trình bậc hai:
Bước 3: Tính đạo hàm bậc hai của hàm số:
Bước 4: Xác định giá trị cực đại và cực tiểu:
- Tại \(x_1 = 3\): \(f''(3) = -12(3) + 6 = -30\) (Âm) → Hàm số đạt cực đại tại \(x = 3\).
- Tại \(x_2 = -2\): \(f''(-2) = -12(-2) + 6 = 30\) (Dương) → Hàm số đạt cực tiểu tại \(x = -2\).
Bước 5: Tính giá trị cực đại và cực tiểu tương ứng:
Vậy, giá trị cực đại của hàm số là \(82\) tại \(x = 3\), và giá trị cực tiểu là \(-43\) tại \(x = -2\).

Bài Tập Toán: Tích Phân Bất Định
Tích phân bất định là một khái niệm quan trọng trong giải tích, liên quan đến việc tìm nguyên hàm của một hàm số. Dưới đây là một số ví dụ và bài tập giúp bạn hiểu rõ hơn về tích phân bất định.
1. Khái niệm cơ bản
Tích phân bất định của một hàm số \(f(x)\) được ký hiệu là:
\[
\int f(x) \, dx
\]
và nó biểu thị tất cả các nguyên hàm của \(f(x)\). Tích phân bất định thường được viết kèm với một hằng số tùy ý \(C\), vì nguyên hàm của một hàm số không phải là duy nhất.
2. Ví dụ về tích phân bất định
- \(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\) (với \(n \neq -1\))
- \(\int e^x \, dx = e^x + C\)
- \(\int \sin(x) \, dx = -\cos(x) + C\)
- \(\int \cos(x) \, dx = \sin(x) + C\)
- \(\int \frac{1}{x} \, dx = \ln|x| + C\) (với \(x \neq 0\))
3. Bài tập thực hành
- Tính tích phân bất định của hàm số \(f(x) = 2x^3 - 3x^2 + 4x - 5\).
- Tính tích phân bất định của hàm số \(f(x) = \frac{1}{x^2 + 1}\).
- Tính tích phân bất định của hàm số \(f(x) = \cos(2x)\).
- Tính tích phân bất định của hàm số \(f(x) = e^{3x}\).
- Tìm nguyên hàm của hàm số \(f(x) = \frac{2x}{\sqrt{x^2 + 1}}\).
4. Hướng dẫn giải bài tập
-
Hàm số \(f(x) = 2x^3 - 3x^2 + 4x - 5\) có tích phân bất định là:
\[
\int (2x^3 - 3x^2 + 4x - 5) \, dx = \frac{2x^4}{4} - \frac{3x^3}{3} + \frac{4x^2}{2} - 5x + C
\]Kết quả là:
\[
\frac{x^4}{2} - x^3 + 2x^2 - 5x + C
\] -
Tích phân của hàm số \(f(x) = \frac{1}{x^2 + 1}\) là:
\[
\int \frac{1}{x^2 + 1} \, dx = \arctan(x) + C
\] -
Hàm số \(f(x) = \cos(2x)\) có tích phân bất định là:
\[
\int \cos(2x) \, dx = \frac{\sin(2x)}{2} + C
\] -
Hàm số \(f(x) = e^{3x}\) có tích phân bất định là:
\[
\int e^{3x} \, dx = \frac{e^{3x}}{3} + C
\] -
Để tìm nguyên hàm của hàm số \(f(x) = \frac{2x}{\sqrt{x^2 + 1}}\), ta có thể đặt \(u = x^2 + 1\), sau đó tính tích phân:
\[
\int \frac{2x}{\sqrt{x^2 + 1}} \, dx = \int \frac{du}{\sqrt{u}} = 2\sqrt{u} + C = 2\sqrt{x^2 + 1} + C
\]
5. Lưu ý khi tính tích phân bất định
- Luôn nhớ thêm hằng số \(C\) vào kết quả cuối cùng của tích phân bất định.
- Sử dụng các phương pháp như đổi biến số, tích phân từng phần để giải các bài toán phức tạp hơn.
- Kiểm tra kết quả bằng cách lấy đạo hàm của nguyên hàm vừa tìm được để xác nhận có khớp với hàm ban đầu hay không.
XEM THÊM:
Bài Tập Toán: Giải Hệ Phương Trình Tuyến Tính
Trong toán học, hệ phương trình tuyến tính là một tập hợp gồm nhiều phương trình tuyến tính, được biểu diễn dưới dạng:
\[
\begin{cases}
a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\
a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2 \\
\vdots \\
a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m
\end{cases}
\]
Với:
- \(a_{ij}\): Hệ số của biến \(x_j\) trong phương trình thứ \(i\).
- \(x_j\): Biến số cần tìm.
- \(b_i\): Hằng số tự do trong phương trình thứ \(i\).
Để giải hệ phương trình này, ta có thể sử dụng nhiều phương pháp khác nhau như:
- Phương pháp thế: Biểu diễn một biến theo các biến khác từ một phương trình, sau đó thay thế vào các phương trình còn lại.
- Phương pháp cộng đại số: Cộng hoặc trừ các phương trình để loại bỏ một biến và giải dần dần cho các biến còn lại.
- Phương pháp ma trận: Biểu diễn hệ phương trình dưới dạng ma trận, sau đó sử dụng phép biến đổi ma trận để giải.
Dưới đây là một ví dụ về hệ phương trình tuyến tính:
\[
\begin{cases}
2x + 3y = 5 \\
4x - y = 1
\end{cases}
\]
Ta có thể giải hệ phương trình này bằng phương pháp cộng đại số như sau:
- Nhân phương trình thứ hai với \(3\) để có hệ số của \(y\) bằng nhau: \[ \begin{cases} 2x + 3y = 5 \\ 12x - 3y = 3 \end{cases} \]
- Cộng hai phương trình: \[ 14x = 8 \Rightarrow x = \frac{8}{14} = \frac{4}{7} \]
- Thay \(x = \frac{4}{7}\) vào một trong hai phương trình ban đầu để tìm \(y\): \[ 2\left(\frac{4}{7}\right) + 3y = 5 \Rightarrow 3y = 5 - \frac{8}{7} = \frac{27}{7} \Rightarrow y = \frac{9}{7} \]
Vậy nghiệm của hệ phương trình là \(x = \frac{4}{7}, y = \frac{9}{7}\).

Bài Tập Toán: Hình Học Không Gian
Hình học không gian là một lĩnh vực toán học tập trung vào việc nghiên cứu các hình khối trong không gian ba chiều, bao gồm các khối đa diện, khối tròn xoay, và các hình dạng phức tạp hơn. Để giải quyết bài tập hình học không gian, ta cần nắm vững các khái niệm về điểm, đường thẳng, mặt phẳng, và các phép tính liên quan đến diện tích, thể tích.
Dưới đây là một ví dụ về bài toán hình học không gian cơ bản:
Ví dụ 1: Tính thể tích khối lăng trụ
Giả sử bạn có một khối lăng trụ đứng tam giác ABC với chiều cao \( h = 12 \, \text{cm} \) và diện tích đáy \( S_{đáy} = 30 \, \text{cm}^2 \). Hãy tính thể tích của khối lăng trụ này.
Giải:
Thể tích của khối lăng trụ được tính theo công thức:
Thay các giá trị đã biết vào công thức:
Vậy, thể tích của khối lăng trụ là \( 360 \, \text{cm}^3 \).
Ví dụ 2: Tính diện tích toàn phần của hình nón
Một hình nón có bán kính đáy \( r = 5 \, \text{cm} \) và đường sinh \( l = 13 \, \text{cm} \). Tính diện tích toàn phần của hình nón này.
Giải:
Diện tích toàn phần của hình nón được tính theo công thức:
Thay các giá trị vào công thức:
Vậy, diện tích toàn phần của hình nón là \( 90\pi \, \text{cm}^2 \).
Bài Tập Tự Giải
- Tính thể tích của một hình chóp tứ giác đều có cạnh đáy dài 6 cm và chiều cao 10 cm.
- Tìm diện tích xung quanh của một hình trụ có chiều cao 8 cm và bán kính đáy 4 cm.
- Một hình cầu có bán kính 7 cm. Hãy tính thể tích và diện tích mặt cầu.

Bài Tập Toán: Tính Diện Tích Hình Phẳng
Trong toán học, diện tích của một hình phẳng có thể được tính thông qua tích phân xác định. Đây là một phần quan trọng trong giải tích và thường được áp dụng trong nhiều bài toán thực tế. Để tính diện tích của một vùng được giới hạn bởi các đường cong, ta cần thực hiện theo các bước sau:
- Xác định hàm số \(f(x)\) biểu diễn đường cong phía trên và hàm số \(g(x)\) biểu diễn đường cong phía dưới.
- Xác định các điểm giao nhau của hai đường cong bằng cách giải phương trình \(f(x) = g(x)\). Các điểm giao này sẽ xác định cận tích phân từ \(a\) đến \(b\).
- Tính diện tích \(A\) bằng cách lấy tích phân của hiệu \(f(x) - g(x)\) trên đoạn \([a, b]\): \[ A = \int_{a}^{b} \left( f(x) - g(x) \right) dx \]
Ví dụ: Tính diện tích hình phẳng giới hạn bởi hai đường cong \(y = x^2\) và \(y = x + 2\).
- Trước tiên, ta xác định hai hàm số \(f(x) = x + 2\) và \(g(x) = x^2\).
- Giải phương trình \(x + 2 = x^2\) để tìm các điểm giao nhau: \[ x^2 - x - 2 = 0 \] Phương trình này có nghiệm là \(x = -1\) và \(x = 2\). Vì vậy, cận tích phân sẽ là từ \(-1\) đến \(2\).
- Diện tích \(A\) được tính bằng: \[ A = \int_{-1}^{2} \left( (x + 2) - x^2 \right) dx \]
- Tính tích phân: \[ A = \int_{-1}^{2} \left( x + 2 - x^2 \right) dx = \left[ \frac{x^2}{2} + 2x - \frac{x^3}{3} \right]_{-1}^{2} \]
- Thay các giá trị cận vào để có kết quả cuối cùng: \[ A = \left( \frac{2^2}{2} + 2(2) - \frac{2^3}{3} \right) - \left( \frac{(-1)^2}{2} + 2(-1) - \frac{(-1)^3}{3} \right) \] \[ = \left( 2 + 4 - \frac{8}{3} \right) - \left( \frac{1}{2} - 2 + \frac{1}{3} \right) \] \[ = \frac{9}{2} - \left( -\frac{11}{6} \right) = \frac{45}{6} + \frac{11}{6} = \frac{56}{6} = \frac{28}{3} \] Vậy diện tích của hình phẳng là \(\frac{28}{3}\) đơn vị diện tích.
Bài Tập Toán: Lý Thuyết Tập Hợp
Lý thuyết tập hợp là một trong những nền tảng quan trọng của toán học, được sử dụng để xác định và phân tích các tập hợp đối tượng, phần tử và mối quan hệ giữa chúng. Dưới đây là một số bài tập cơ bản về lý thuyết tập hợp, kèm theo các bước giải chi tiết.
-
Bài tập 1: Xác định tập hợp con
Cho tập hợp \( A = \{1, 2, 3\} \). Liệt kê tất cả các tập hợp con của \( A \).
Giải:
- Tập hợp rỗng: \( \emptyset \)
- Các tập hợp con có 1 phần tử: \( \{1\}, \{2\}, \{3\} \)
- Các tập hợp con có 2 phần tử: \( \{1, 2\}, \{1, 3\}, \{2, 3\} \)
- Tập hợp con có 3 phần tử: \( \{1, 2, 3\} \)
Vậy tổng số tập hợp con của \( A \) là \( 2^3 = 8 \) tập hợp.
-
Bài tập 2: Phép giao và phép hợp của tập hợp
Cho hai tập hợp \( B = \{1, 2, 3, 4\} \) và \( C = \{3, 4, 5, 6\} \). Tìm:
Phép hợp: \( B \cup C \)
Phép giao: \( B \cap C \)
Giải:
- Phép hợp: \( B \cup C = \{1, 2, 3, 4, 5, 6\} \)
- Phép giao: \( B \cap C = \{3, 4\} \)
-
Bài tập 3: Tìm hiệu của hai tập hợp
Cho hai tập hợp \( D = \{a, b, c\} \) và \( E = \{b, c, d\} \). Tìm:
Hiệu: \( D \setminus E \)
Hiệu: \( E \setminus D \)
Giải:
- Hiệu: \( D \setminus E = \{a\} \)
- Hiệu: \( E \setminus D = \{d\} \)
-
Bài tập 4: Xác định phần bù của tập hợp
Cho tập hợp \( F = \{x \in \mathbb{N} | x \leq 5\} \) và tập hợp \( G = \{1, 2, 3\} \). Tìm phần bù của \( G \) trong \( F \).
Giải:
- Tập hợp \( F = \{1, 2, 3, 4, 5\} \)
- Phần bù của \( G \) trong \( F \): \( F \setminus G = \{4, 5\} \)
Các bài tập trên đây cung cấp những kiến thức cơ bản về lý thuyết tập hợp. Hãy cố gắng giải quyết từng bài tập để nắm vững các khái niệm quan trọng và áp dụng chúng vào những bài toán phức tạp hơn.
Bài Tập Toán: Xác Suất Thống Kê
Xác suất thống kê là một lĩnh vực quan trọng trong toán học, giúp chúng ta hiểu và phân tích các hiện tượng ngẫu nhiên. Dưới đây là một số bài tập cơ bản về xác suất thống kê để bạn luyện tập và nắm vững kiến thức.
Bài Tập 1: Tính Xác Suất
Cho một hộp có 5 viên bi đỏ và 3 viên bi xanh. Một viên bi được rút ngẫu nhiên từ hộp. Hãy tính xác suất để:
- Viên bi được rút ra là màu đỏ.
- Viên bi được rút ra là màu xanh.
Gợi ý: Sử dụng công thức xác suất cơ bản:
\[
P(A) = \frac{\text{số kết quả thuận lợi}}{\text{tổng số kết quả có thể xảy ra}}
\]
Bài Tập 2: Xác Suất Có Điều Kiện
Trong một lớp học, có 10 học sinh nam và 15 học sinh nữ. Một học sinh được chọn ngẫu nhiên. Giả sử học sinh này là nam, hãy tính xác suất để học sinh này có điểm toán trên 8, biết rằng có 4 học sinh nam đạt điều kiện này.
Gợi ý: Áp dụng công thức xác suất có điều kiện:
\[
P(A|B) = \frac{P(A \cap B)}{P(B)}
\]
Bài Tập 3: Phân Phối Xác Suất
Giả sử thời gian chờ xe buýt tại một trạm xe buýt tuân theo phân phối đều trên khoảng từ 0 đến 15 phút. Hãy tính xác suất để thời gian chờ là ít hơn 5 phút.
Gợi ý: Sử dụng kiến thức về phân phối đều:
\[
P(a \leq X \leq b) = \frac{b-a}{B-A}
\]
Bài Tập 4: Phân Phối Nhị Thức
Trong một kỳ thi, xác suất để một học sinh trả lời đúng một câu hỏi là 0.7. Nếu đề thi gồm 10 câu hỏi, hãy tính xác suất để học sinh trả lời đúng ít nhất 8 câu.
Gợi ý: Sử dụng công thức của phân phối nhị thức:
\[
P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}
\]
Bài Tập 5: Định Luật Số Lớn
Một đồng xu được tung 1000 lần. Hãy ước lượng xác suất để số lần xuất hiện mặt ngửa lớn hơn 520 lần.
Gợi ý: Sử dụng định luật số lớn và công thức xác suất gần đúng:
\[
P\left(\left|\frac{S_n}{n} - p\right| < \epsilon\right) \approx 1
\]
Những bài tập trên giúp bạn rèn luyện kỹ năng phân tích và tính toán trong xác suất thống kê. Hãy làm từng bài cẩn thận và kiểm tra lại kết quả của mình để nắm vững kiến thức.
Bài Tập Toán: Số Phức
Số phức là một khái niệm mở rộng của số thực, được biểu diễn dưới dạng \( z = a + bi \) trong đó \( a \) và \( b \) là các số thực, và \( i \) là đơn vị ảo thỏa mãn \( i^2 = -1 \). Dưới đây là một số bài tập để bạn rèn luyện kỹ năng giải quyết các vấn đề liên quan đến số phức.
Bài Tập 1: Tìm Mô-đun và Số Phức Liên Hợp
Cho số phức \( z = 3 - 4i \). Hãy tính mô-đun của số phức và số phức liên hợp của nó.
- Mô-đun của số phức được tính bằng công thức: \(\lvert z \rvert = \sqrt{a^2 + b^2}\)
- Số phức liên hợp được xác định bởi: \(\overline{z} = a - bi\)
Áp dụng công thức:
\[
\lvert z \rvert = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
Số phức liên hợp của \( z \) là \( \overline{z} = 3 + 4i \).
Bài Tập 2: Cộng và Trừ Số Phức
Thực hiện phép tính với các số phức sau: \( z_1 = 2 + 3i \) và \( z_2 = 1 - 4i \). Hãy tính:
- \( z_1 + z_2 \)
- \( z_1 - z_2 \)
Kết quả:
- \( z_1 + z_2 = (2 + 1) + (3i - 4i) = 3 - i \)
- \( z_1 - z_2 = (2 - 1) + (3i + 4i) = 1 + 7i \)
Bài Tập 3: Nhân và Chia Số Phức
Cho \( z_1 = 2 + 2i \) và \( z_2 = 1 + i \). Hãy tính:
- \( z_1 \times z_2 \)
- \( \frac{z_1}{z_2} \)
Kết quả:
- \( z_1 \times z_2 = (2 + 2i)(1 + i) = 2 + 2i + 2i + 2i^2 = 2 + 4i - 2 = 4i \)
- \( \frac{z_1}{z_2} = \frac{(2 + 2i)(1 - i)}{(1 + i)(1 - i)} = \frac{2 - 2i + 2i - 2i^2}{1 - i^2} = \frac{2 + 2}{1 + 1} = \frac{4}{2} = 2 \)
Bài Tập 4: Biểu Diễn Hình Học
Biểu diễn số phức \( z = -3 + 4i \) trên mặt phẳng tọa độ phức.
Điểm tương ứng với số phức \( z = -3 + 4i \) sẽ có tọa độ là \( (-3, 4) \) trên mặt phẳng phức.
Bài Tập 5: Phương Trình Bậc Hai Với Số Phức
Giải phương trình bậc hai \( z^2 + 2z + 5 = 0 \).
Áp dụng công thức nghiệm:
\[
z = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Trong trường hợp này, \( a = 1 \), \( b = 2 \), và \( c = 5 \). Ta có:
\[
z = \frac{-2 \pm \sqrt{2^2 - 4(1)(5)}}{2(1)} = \frac{-2 \pm \sqrt{4 - 20}}{2} = \frac{-2 \pm \sqrt{-16}}{2}
\]
Vì \( \sqrt{-16} = 4i \), ta có:
\[
z = \frac{-2 \pm 4i}{2} = -1 \pm 2i
\]
Vậy nghiệm của phương trình là \( z_1 = -1 + 2i \) và \( z_2 = -1 - 2i \).