Chủ đề giải bóng đá ngoại hạng anh đêm nay: Giải bóng đá Ngoại hạng Anh đêm nay hứa hẹn sẽ mang đến những trận cầu đầy kịch tính với sự tham gia của các đội bóng hàng đầu. Khám phá lịch thi đấu chi tiết, nhận định chuyên sâu và cập nhật tình hình lực lượng của các đội bóng trước giờ bóng lăn. Đừng bỏ lỡ cơ hội theo dõi những khoảnh khắc đáng nhớ của mùa giải!
Mục lục
- Kết quả tìm kiếm về "Giải bóng đá Ngoại hạng Anh đêm nay"
- Mục lục tổng hợp nội dung các bài viết
- Bài tập Toán học
- Bài tập 1: Giải hệ phương trình bậc nhất
- Bài tập 2: Tính giới hạn của dãy số
- Bài tập 3: Tìm nghiệm của phương trình bậc hai
- Bài tập 4: Tính diện tích hình học phẳng
- Bài tập 5: Đạo hàm và ứng dụng trong bài toán cực trị
- Bài tập 6: Tích phân và diện tích hình phẳng
- Bài tập 7: Giải bất phương trình
- Bài tập 8: Phân tích đa thức thành nhân tử
- Bài tập 9: Tính chu vi và diện tích của hình tròn
- Bài tập 10: Tính thể tích của hình khối không gian
Kết quả tìm kiếm về "Giải bóng đá Ngoại hạng Anh đêm nay"
Giải bóng đá Ngoại hạng Anh luôn thu hút sự quan tâm lớn từ người hâm mộ với những trận đấu hấp dẫn diễn ra hàng tuần. Dưới đây là thông tin chi tiết về các trận đấu diễn ra đêm nay:
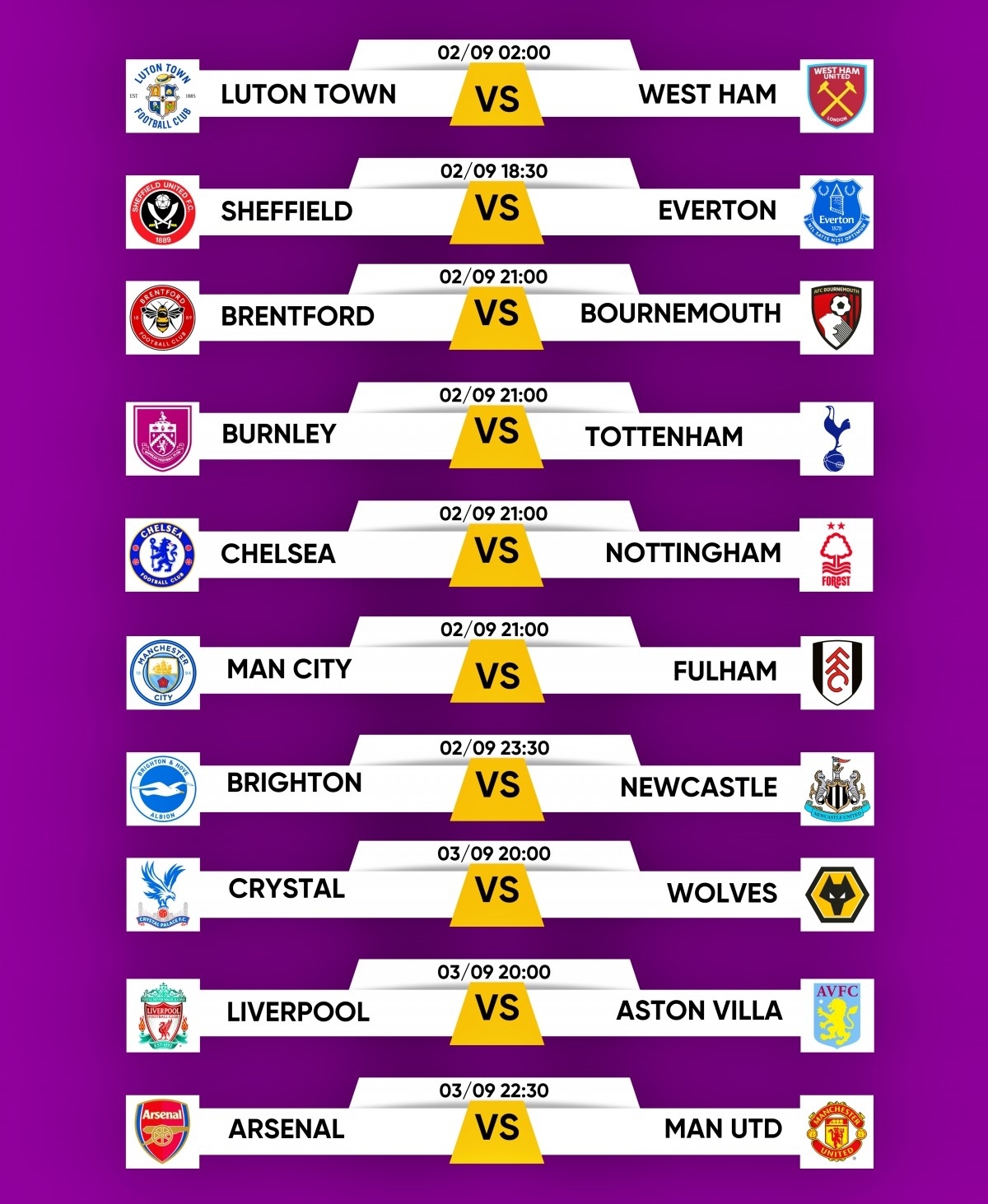
1. Lịch thi đấu
- Trận đấu tâm điểm: Cuộc đối đầu giữa Chelsea và Liverpool diễn ra vào lúc 23:30 trên sân Stamford Bridge.
- Các trận đấu khác:
- Everton vs Manchester City - 21:00
- Arsenal vs Tottenham - 19:30
- Brighton vs Newcastle - 21:00
2. Tình hình lực lượng
Cả Chelsea và Liverpool đều gặp khó khăn với danh sách chấn thương dài. Chelsea thiếu vắng các cầu thủ chủ chốt như Reece James và Ben Chilwell, trong khi Liverpool không có sự phục vụ của Andy Robertson và Thiago Alcantara.
3. Bảng xếp hạng
Trước các trận đấu đêm nay, thứ hạng của các đội trong nhóm dẫn đầu như sau:
| Đội | Trận | Điểm |
| 1. Manchester City | 4 | 12 |
| 2. Arsenal | 4 | 10 |
| 3. Liverpool | 4 | 10 |
4. Dự đoán kết quả
Trận đấu giữa Chelsea và Liverpool được dự đoán sẽ rất kịch tính. Chuyên gia đánh giá khả năng chiến thắng của Liverpool là cao hơn dựa trên phong độ hiện tại và lịch sử đối đầu.
5. Đón xem
Người hâm mộ có thể theo dõi trực tiếp các trận đấu trên các kênh thể thao phổ biến hoặc qua các nền tảng trực tuyến như VTV Go và K+.
.png)
Mục lục tổng hợp nội dung các bài viết
- Lịch thi đấu và thời gian các trận đấu: Cập nhật chi tiết về lịch thi đấu đêm nay, bao gồm các trận đấu quan trọng như Chelsea vs Liverpool và các trận đấu khác.
- Nhận định và phân tích trước trận đấu: Đánh giá cơ hội chiến thắng, phân tích chiến thuật của các đội và dự đoán kết quả trận đấu.
- Tình hình lực lượng các đội: Thông tin về chấn thương, án phạt và đội hình dự kiến của các đội bóng trước khi ra sân.
- Bảng xếp hạng hiện tại: Cập nhật thứ hạng các đội bóng trước loạt trận đêm nay, bao gồm điểm số và vị trí của các đội trong bảng xếp hạng.
- Lịch sử đối đầu và phong độ gần đây: So sánh kết quả đối đầu giữa các đội bóng, cùng với phong độ trong 5 trận gần nhất.
- Những cầu thủ nổi bật: Danh sách các cầu thủ có phong độ cao, đóng vai trò quan trọng trong trận đấu.
- Kênh phát sóng và cách theo dõi trực tiếp: Hướng dẫn xem trực tiếp các trận đấu trên các kênh truyền hình và nền tảng trực tuyến.
- Tin tức bên lề: Các thông tin thú vị liên quan đến giải đấu như chuyển nhượng, phát ngôn của huấn luyện viên và cầu thủ.
- Thống kê và thành tích: Thống kê về số bàn thắng, số lần giữ sạch lưới và các chỉ số quan trọng khác của các đội.
- Dự đoán tỷ số từ chuyên gia: Ý kiến và dự đoán tỷ số từ các chuyên gia bóng đá hàng đầu.
Bài tập Toán học
- Bài tập 1: Giải hệ phương trình tuyến tính
Cho hệ phương trình sau:
\[ \begin{cases} 2x + 3y = 5 \\ 4x - y = 11 \end{cases} \]Giải hệ phương trình trên và tìm giá trị của \(x\) và \(y\).
- Bài tập 2: Tính giới hạn của dãy số
Tính giới hạn của dãy số sau khi \(n \to \infty\):
\[ a_n = \frac{3n^2 + 2n + 1}{2n^2 + n + 4} \] - Bài tập 3: Tìm nghiệm của phương trình bậc hai
Giải phương trình bậc hai sau:
\[ x^2 - 5x + 6 = 0 \]Xác định các nghiệm của phương trình.
- Bài tập 4: Tính diện tích hình học phẳng
Cho tam giác có các đỉnh \(A(1,2)\), \(B(4,6)\), \(C(6,3)\). Tính diện tích của tam giác.
- Bài tập 5: Đạo hàm và ứng dụng trong bài toán cực trị
Tìm giá trị lớn nhất và nhỏ nhất của hàm số:
\[ f(x) = x^3 - 3x^2 + 4 \]trên đoạn \([0, 3]\).
- Bài tập 6: Tích phân và diện tích hình phẳng
Tính tích phân sau:
\[ \int_{0}^{2} (2x^2 - 3x + 1) \, dx \]và tìm diện tích hình phẳng giới hạn bởi đồ thị của hàm số và trục hoành.
- Bài tập 7: Giải bất phương trình
Giải bất phương trình sau:
\[ 2x + 1 > 3x - 2 \] - Bài tập 8: Phân tích đa thức thành nhân tử
Phân tích đa thức sau thành nhân tử:
\[ x^3 - 6x^2 + 11x - 6 \] - Bài tập 9: Tính chu vi và diện tích của hình tròn
Tính chu vi và diện tích của hình tròn có bán kính \(r = 5\).
- Bài tập 10: Tính thể tích của hình khối không gian
Tính thể tích của hình nón có chiều cao \(h = 10\) và bán kính đáy \(r = 3\).

Bài tập 1: Giải hệ phương trình bậc nhất
Cho hệ phương trình tuyến tính sau:
Để giải hệ phương trình này, chúng ta thực hiện các bước sau:
- Bước 1: Biểu diễn y từ phương trình thứ hai
Từ phương trình \(4x - y = 7\), ta biểu diễn y như sau:
\[ y = 4x - 7 \] - Bước 2: Thay giá trị của y vào phương trình thứ nhất
Thay \(y = 4x - 7\) vào phương trình đầu tiên \(3x + 2y = 5\), ta có:
\[ 3x + 2(4x - 7) = 5 \]Giải phương trình này để tìm x:
\[ 3x + 8x - 14 = 5 \\ 11x = 19 \\ x = \frac{19}{11} \] - Bước 3: Tìm y bằng cách thay giá trị của x vào phương trình đã biểu diễn y
Thay \(x = \frac{19}{11}\) vào phương trình \(y = 4x - 7\):
\[ y = 4\left(\frac{19}{11}\right) - 7 \\ y = \frac{76}{11} - \frac{77}{11} \\ y = -\frac{1}{11} \] - Bước 4: Kết luận
Vậy nghiệm của hệ phương trình là:
\[ x = \frac{19}{11}, \quad y = -\frac{1}{11} \]
Bài tập 2: Tính giới hạn của dãy số
Cho dãy số \(a_n\) với biểu thức sau:
Để tính giới hạn của dãy số khi \(n \to \infty\), ta thực hiện các bước sau:
- Bước 1: Chia cả tử và mẫu của biểu thức cho \(n^2\)
Chia cả tử và mẫu cho \(n^2\) để đơn giản hóa biểu thức:
\[ a_n = \frac{\frac{5n^2}{n^2} + \frac{3n}{n^2} + \frac{2}{n^2}}{\frac{2n^2}{n^2} + \frac{n}{n^2} + \frac{1}{n^2}} = \frac{5 + \frac{3}{n} + \frac{2}{n^2}}{2 + \frac{1}{n} + \frac{1}{n^2}} \] - Bước 2: Tính giới hạn khi \(n \to \infty\)
Khi \(n \to \infty\), các thành phần chứa \( \frac{1}{n} \) và \( \frac{1}{n^2} \) trong tử số và mẫu số sẽ tiến dần về 0, do đó ta có:
\[ \lim_{n \to \infty} a_n = \frac{5 + 0 + 0}{2 + 0 + 0} = \frac{5}{2} \] - Bước 3: Kết luận
Giới hạn của dãy số \(a_n\) khi \(n \to \infty\) là:
\[ \lim_{n \to \infty} a_n = \frac{5}{2} \]

Bài tập 3: Tìm nghiệm của phương trình bậc hai
Phương trình bậc hai có dạng tổng quát là:
\[ ax^2 + bx + c = 0 \]
Trong đó:
- \( a, b, c \) là các hệ số của phương trình, với \( a \neq 0 \).
Để tìm nghiệm của phương trình bậc hai, ta sử dụng công thức nghiệm sau:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Quy trình tìm nghiệm gồm các bước sau:
- Bước 1: Xác định các hệ số \( a, b, c \) từ phương trình đã cho.
- Bước 2: Tính delta \( \Delta = b^2 - 4ac \).
- Bước 3: Xét giá trị của \( \Delta \):
- Nếu \( \Delta > 0 \): Phương trình có hai nghiệm phân biệt.
- Nếu \( \Delta = 0 \): Phương trình có một nghiệm kép.
- Nếu \( \Delta < 0 \): Phương trình vô nghiệm trong tập số thực.
- Bước 4: Sử dụng công thức nghiệm để tìm giá trị của \( x_1 \) và \( x_2 \) (nếu có).
Ví dụ, giải phương trình bậc hai sau:
\[ 2x^2 - 4x + 1 = 0 \]
Ta có:
- \( a = 2 \)
- \( b = -4 \)
- \( c = 1 \)
Delta:
\[ \Delta = (-4)^2 - 4 \times 2 \times 1 = 16 - 8 = 8 \]
Vì \( \Delta > 0 \), phương trình có hai nghiệm phân biệt:
\[ x_1 = \frac{-(-4) + \sqrt{8}}{2 \times 2} = \frac{4 + 2\sqrt{2}}{4} = 1 + \frac{\sqrt{2}}{2} \]
\[ x_2 = \frac{-(-4) - \sqrt{8}}{2 \times 2} = \frac{4 - 2\sqrt{2}}{4} = 1 - \frac{\sqrt{2}}{2} \]
Vậy, nghiệm của phương trình là \( x_1 = 1 + \frac{\sqrt{2}}{2} \) và \( x_2 = 1 - \frac{\sqrt{2}}{2} \).
XEM THÊM:
Bài tập 4: Tính diện tích hình học phẳng
Trong toán học, việc tính diện tích của các hình học phẳng là một trong những bài toán cơ bản nhưng rất quan trọng. Chúng ta sẽ cùng tìm hiểu cách tính diện tích của một số hình học cơ bản như hình chữ nhật, hình tam giác, hình tròn và hình thang.
1. Hình chữ nhật
Diện tích của hình chữ nhật được tính bằng công thức:
\[ S = a \times b \]
Trong đó:
- \( S \) là diện tích của hình chữ nhật
- \( a \) là chiều dài
- \( b \) là chiều rộng
2. Hình tam giác
Diện tích của hình tam giác được tính bằng công thức:
\[ S = \frac{1}{2} \times a \times h \]
Trong đó:
- \( S \) là diện tích của hình tam giác
- \( a \) là độ dài của đáy
- \( h \) là chiều cao ứng với đáy
3. Hình tròn
Diện tích của hình tròn được tính bằng công thức:
\[ S = \pi \times r^2 \]
Trong đó:
- \( S \) là diện tích của hình tròn
- \( r \) là bán kính của hình tròn
- \( \pi \) là hằng số Pi (khoảng 3.14159)
4. Hình thang
Diện tích của hình thang được tính bằng công thức:
\[ S = \frac{(a + b) \times h}{2} \]
Trong đó:
- \( S \) là diện tích của hình thang
- \( a \) và \( b \) là độ dài của hai đáy
- \( h \) là chiều cao
5. Ví dụ minh họa
Giả sử bạn cần tính diện tích của một hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm. Áp dụng công thức:
\[ S = 5 \times 3 = 15 \text{ cm}^2 \]
Vậy diện tích của hình chữ nhật này là 15 cm2.
Bài tập 5: Đạo hàm và ứng dụng trong bài toán cực trị
Trong toán học, đạo hàm là một khái niệm cơ bản trong giải tích, được sử dụng để xác định tốc độ thay đổi của một hàm số khi biến số thay đổi. Đạo hàm còn là công cụ quan trọng trong việc giải quyết các bài toán cực trị, nơi mà ta cần tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số.
1. Khái niệm cơ bản về đạo hàm
- Đạo hàm của hàm số \(f(x)\) tại điểm \(x_0\) được định nghĩa là giới hạn: \[ f'(x_0) = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \]
- Đạo hàm còn được ký hiệu là \(f'(x)\), \(\frac{dy}{dx}\), hoặc \(Df(x)\).
2. Ứng dụng của đạo hàm trong bài toán cực trị
Đạo hàm có vai trò quan trọng trong việc tìm cực trị của hàm số. Để tìm các điểm cực trị (cực đại hoặc cực tiểu) của hàm số \(f(x)\), ta cần thực hiện các bước sau:
Bước 1: Tính đạo hàm bậc nhất
Đầu tiên, ta tính đạo hàm bậc nhất \(f'(x)\) của hàm số.
Bước 2: Giải phương trình \(f'(x) = 0\)
Giải phương trình \(f'(x) = 0\) để tìm các điểm \(x_0\) mà tại đó hàm số có thể đạt cực trị.
Bước 3: Xác định tính chất của điểm cực trị
Để xác định tính chất của các điểm tìm được từ Bước 2, ta cần xem xét dấu của đạo hàm bậc hai \(f''(x)\) tại các điểm đó:
- Nếu \(f''(x_0) > 0\), thì \(x_0\) là điểm cực tiểu.
- Nếu \(f''(x_0) < 0\), thì \(x_0\) là điểm cực đại.
- Nếu \(f''(x_0) = 0\), cần xem xét kỹ hơn hoặc sử dụng phương pháp khác để xác định tính chất của điểm đó.
3. Ví dụ minh họa
Cho hàm số \(f(x) = x^3 - 3x^2 + 2\), ta thực hiện các bước sau để tìm cực trị:
- Tính đạo hàm: \[ f'(x) = 3x^2 - 6x \]
- Giải phương trình: \[ 3x^2 - 6x = 0 \Rightarrow x(3x - 6) = 0 \Rightarrow x = 0 \text{ hoặc } x = 2 \]
- Xác định tính chất của các điểm:
- Tại \(x = 0\), ta có \(f''(0) = -6 < 0\) nên \(x = 0\) là điểm cực đại.
- Tại \(x = 2\), ta có \(f''(2) = 6 > 0\) nên \(x = 2\) là điểm cực tiểu.
Do đó, hàm số có cực đại tại \(x = 0\) và cực tiểu tại \(x = 2\).

Bài tập 6: Tích phân và diện tích hình phẳng
Trong bài tập này, chúng ta sẽ tìm hiểu về cách tính diện tích của một vùng hình phẳng giới hạn bởi các đường cong bằng phương pháp tích phân. Đây là một ứng dụng quan trọng của tích phân trong Toán học và có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau.
1. Định nghĩa tích phân xác định
Tích phân xác định của hàm số \(f(x)\) trên đoạn \([a, b]\) được định nghĩa là:
\[
\int_{a}^{b} f(x) \,dx
\]
Tích phân này biểu diễn diện tích của vùng dưới đồ thị của hàm số \(f(x)\) từ \(x = a\) đến \(x = b\).
2. Tính diện tích của một hình phẳng
Để tính diện tích hình phẳng giới hạn bởi các đường cong \(y = f(x)\), \(y = g(x)\), và các đường thẳng \(x = a\), \(x = b\), ta sử dụng công thức:
\[
A = \int_{a}^{b} |f(x) - g(x)| \,dx
\]
Ở đây, \(f(x)\) và \(g(x)\) là hai hàm số liên tục trên đoạn \([a, b]\), và ta lấy giá trị tuyệt đối của hiệu giữa chúng để đảm bảo kết quả tích phân là diện tích dương.
3. Ví dụ cụ thể
Giả sử chúng ta cần tính diện tích hình phẳng giới hạn bởi đường cong \(y = x^2\) và đường thẳng \(y = x + 2\) từ \(x = -1\) đến \(x = 2\). Đầu tiên, chúng ta tính hiệu của hai hàm số:
\[
A = \int_{-1}^{2} |x + 2 - x^2| \,dx
\]
Sau khi tính tích phân này, ta sẽ có được diện tích của vùng hình phẳng cần tìm.
4. Kết luận
Phương pháp tích phân là công cụ mạnh mẽ để tính toán diện tích của các hình phẳng phức tạp. Việc hiểu rõ và áp dụng đúng các công thức tích phân giúp chúng ta giải quyết các bài toán một cách chính xác và hiệu quả.
Bài tập 7: Giải bất phương trình
Bất phương trình là một phần quan trọng trong toán học, giúp xác định các giá trị của biến mà làm cho một bất đẳng thức trở thành đúng. Dưới đây là các bước chi tiết để giải một bài toán bất phương trình.
-
Xác định bất phương trình: Trước tiên, ta cần xác định rõ ràng bất phương trình cần giải. Bất phương trình có dạng tổng quát là:
\[ ax + b > 0 \]
hoặc có thể là dạng phức tạp hơn như:
\[ ax^2 + bx + c \leq 0 \]
-
Biến đổi tương đương: Sử dụng các phép biến đổi tương đương như cộng, trừ, nhân, chia cả hai vế của bất phương trình với một số hoặc biểu thức phù hợp. Chú ý rằng nếu nhân hoặc chia với một số âm, dấu bất phương trình phải được đảo ngược.
-
Phân tích nghiệm: Sau khi biến đổi tương đương, ta sẽ thu được một bất phương trình đơn giản hơn. Bước tiếp theo là phân tích để tìm ra nghiệm của bất phương trình này.
Ví dụ, giải bất phương trình sau:
\[ x^2 - 4x + 3 < 0 \]
Chúng ta có thể phân tích thành:
\[ (x - 1)(x - 3) < 0 \]
-
Xác định khoảng nghiệm: Từ phép phân tích trên, xác định các khoảng giá trị của biến \(x\) để thỏa mãn bất phương trình. Trong ví dụ trên, nghiệm của bất phương trình là:
\[ 1 < x < 3 \]
-
Biểu diễn kết quả: Cuối cùng, nghiệm của bất phương trình thường được biểu diễn dưới dạng tập hợp các khoảng giá trị, có thể là dưới dạng biểu thức hoặc trên trục số.
Để làm chủ kỹ năng giải bất phương trình, học sinh cần luyện tập nhiều và nắm vững các quy tắc cơ bản, cũng như biết cách xử lý các trường hợp đặc biệt. Chúc các bạn học tốt!

Bài tập 8: Phân tích đa thức thành nhân tử
Trong bài học này, chúng ta sẽ cùng tìm hiểu về phương pháp phân tích đa thức thành nhân tử. Đây là một kỹ năng cơ bản nhưng rất quan trọng trong toán học, giúp chúng ta giải quyết nhiều bài toán phức tạp một cách dễ dàng hơn. Phân tích đa thức thành nhân tử có thể thực hiện bằng nhiều phương pháp khác nhau, dưới đây là một số phương pháp thường gặp:
- Phương pháp đặt nhân tử chung: Đây là phương pháp đơn giản nhất. Ta sẽ tìm nhân tử chung của các hạng tử trong đa thức rồi đặt nó ra ngoài.
- Phương pháp nhóm hạng tử: Ta nhóm các hạng tử có nhân tử chung lại với nhau rồi áp dụng phương pháp đặt nhân tử chung.
- Phương pháp dùng hằng đẳng thức: Sử dụng các hằng đẳng thức quen thuộc như \((a + b)^2 = a^2 + 2ab + b^2\), \((a - b)^2 = a^2 - 2ab + b^2\), hay \((a + b)(a - b) = a^2 - b^2\) để phân tích.
- Phương pháp phân tích đa thức bậc ba: Đối với các đa thức bậc ba, ta có thể sử dụng công thức nghiệm hoặc thử các giá trị của biến để tìm ra một nghiệm đơn giản, sau đó phân tích thành nhân tử.
Ví dụ: \[2x^3 + 4x^2 + 6x = 2x(x^2 + 2x + 3)\]
Ví dụ: \[x^3 + 3x^2 + 2x + 6 = (x^3 + 3x^2) + (2x + 6) = x^2(x + 3) + 2(x + 3) = (x^2 + 2)(x + 3)\]
Ví dụ: \[x^2 - 9 = (x - 3)(x + 3)\]
Ví dụ: \[x^3 - 6x^2 + 11x - 6 = (x - 1)(x - 2)(x - 3)\]
Việc thành thạo các phương pháp trên sẽ giúp bạn xử lý các bài toán phân tích đa thức thành nhân tử một cách nhanh chóng và hiệu quả. Hãy luyện tập thật nhiều để nắm vững kiến thức này!
Bài tập 9: Tính chu vi và diện tích của hình tròn
Trong bài học này, chúng ta sẽ học cách tính chu vi và diện tích của một hình tròn. Đây là một trong những bài toán cơ bản nhưng rất quan trọng trong hình học phẳng. Để bắt đầu, chúng ta cần hiểu rõ các công thức liên quan đến hình tròn:
- Chu vi của hình tròn: Chu vi của một hình tròn được tính bằng công thức \[C = 2\pi r\], trong đó \(r\) là bán kính của hình tròn và \(\pi\) là hằng số Pi, xấp xỉ bằng 3.14159.
- Diện tích của hình tròn: Diện tích của một hình tròn được tính bằng công thức \[A = \pi r^2\], trong đó \(r\) là bán kính của hình tròn.
Hãy cùng thực hiện một ví dụ cụ thể:
- Giả sử chúng ta có một hình tròn với bán kính \(r = 5\) cm.
- Tính chu vi: Áp dụng công thức tính chu vi:
\[
C = 2\pi r = 2 \times 3.14159 \times 5 \approx 31.4159 \, \text{cm}
\] - Tính diện tích: Áp dụng công thức tính diện tích:
\[
A = \pi r^2 = 3.14159 \times 5^2 = 3.14159 \times 25 \approx 78.53975 \, \text{cm}^2
\]
Qua ví dụ trên, chúng ta có thể thấy rằng việc tính chu vi và diện tích của một hình tròn khá đơn giản nếu như chúng ta nắm vững các công thức cơ bản. Hãy luyện tập nhiều hơn với các giá trị bán kính khác nhau để thuần thục kỹ năng này!
Bài tập 10: Tính thể tích của hình khối không gian
Trong toán học không gian, tính thể tích của các hình khối là một kỹ năng quan trọng giúp chúng ta hiểu rõ hơn về đặc tính ba chiều của các vật thể. Dưới đây là các công thức cơ bản để tính thể tích của một số hình khối phổ biến:
- Thể tích của hình lập phương: Hình lập phương có các cạnh bằng nhau, thể tích được tính bằng công thức \[V = a^3\], trong đó \(a\) là độ dài cạnh của hình lập phương.
- Thể tích của hình hộp chữ nhật: Thể tích của hình hộp chữ nhật được tính bằng công thức \[V = l \times w \times h\], trong đó \(l\) là chiều dài, \(w\) là chiều rộng, và \(h\) là chiều cao.
- Thể tích của hình trụ: Hình trụ có thể tích được tính bằng công thức \[V = \pi r^2 h\], trong đó \(r\) là bán kính đáy và \(h\) là chiều cao của hình trụ.
- Thể tích của hình cầu: Thể tích của hình cầu được tính bằng công thức \[V = \frac{4}{3} \pi r^3\], trong đó \(r\) là bán kính của hình cầu.
- Thể tích của hình nón: Thể tích của hình nón được tính bằng công thức \[V = \frac{1}{3} \pi r^2 h\], trong đó \(r\) là bán kính đáy và \(h\) là chiều cao của hình nón.
Ví dụ: Giả sử chúng ta có một hình trụ với bán kính đáy \(r = 3\) cm và chiều cao \(h = 10\) cm. Hãy tính thể tích của hình trụ này:
- Áp dụng công thức tính thể tích cho hình trụ:
\[
V = \pi r^2 h = \pi \times 3^2 \times 10 = \pi \times 9 \times 10 = 90\pi \, \text{cm}^3
\] - Với \(\pi \approx 3.14159\), thể tích của hình trụ là:
\[
V \approx 90 \times 3.14159 = 282.743 \, \text{cm}^3
\]
Qua ví dụ trên, chúng ta thấy rằng việc tính thể tích của các hình khối không gian yêu cầu nắm vững các công thức cơ bản. Hãy tiếp tục luyện tập với các bài toán khác để thành thạo kỹ năng này!