Chủ đề kết quả lịch thi đấu bóng đá việt nam: Kết quả lịch thi đấu bóng đá Việt Nam được cập nhật nhanh chóng và chính xác nhất. Bài viết này mang đến thông tin mới nhất về các trận đấu, kết quả, và lịch thi đấu của đội tuyển Việt Nam, giúp người hâm mộ không bỏ lỡ bất kỳ trận đấu quan trọng nào.
Mục lục
- Kết quả và Lịch thi đấu bóng đá Việt Nam
- Mục lục tổng hợp thông tin về kết quả và lịch thi đấu bóng đá Việt Nam
- Dạng bài tập Toán học: Giải phương trình bậc hai
- Dạng bài tập Vật lý: Tính vận tốc trong chuyển động đều
- Dạng bài tập Tiếng Anh: Sử dụng thì quá khứ đơn
- Dạng bài tập Toán học: Phân tích đa thức thành nhân tử
- Dạng bài tập Vật lý: Định luật Bảo toàn năng lượng
- Dạng bài tập Tiếng Anh: Viết lại câu sử dụng câu điều kiện loại 1
- Dạng bài tập Toán học: Giải hệ phương trình bậc nhất hai ẩn
- Dạng bài tập Vật lý: Tính lực trong các hệ cân bằng
- Dạng bài tập Tiếng Anh: Hoàn thành câu với từ cho trước
- Dạng bài tập Toán học: Giải phương trình vô tỉ
Kết quả và Lịch thi đấu bóng đá Việt Nam
Trang này cung cấp thông tin chi tiết về kết quả và lịch thi đấu bóng đá của các đội tuyển Việt Nam, bao gồm các giải đấu quốc nội và quốc tế. Các dữ liệu được cập nhật liên tục, giúp người hâm mộ dễ dàng theo dõi và nắm bắt tình hình thi đấu của các đội tuyển yêu thích.
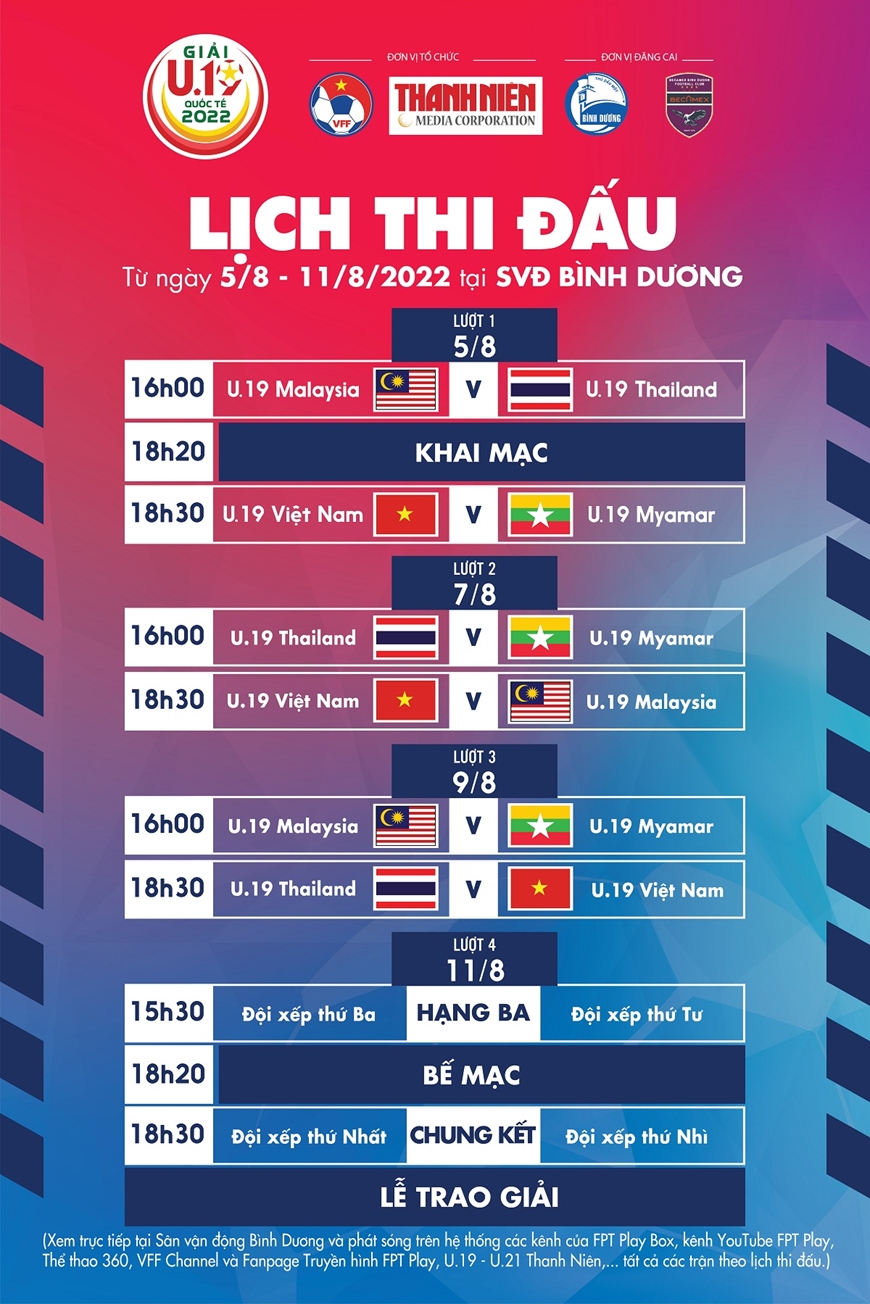
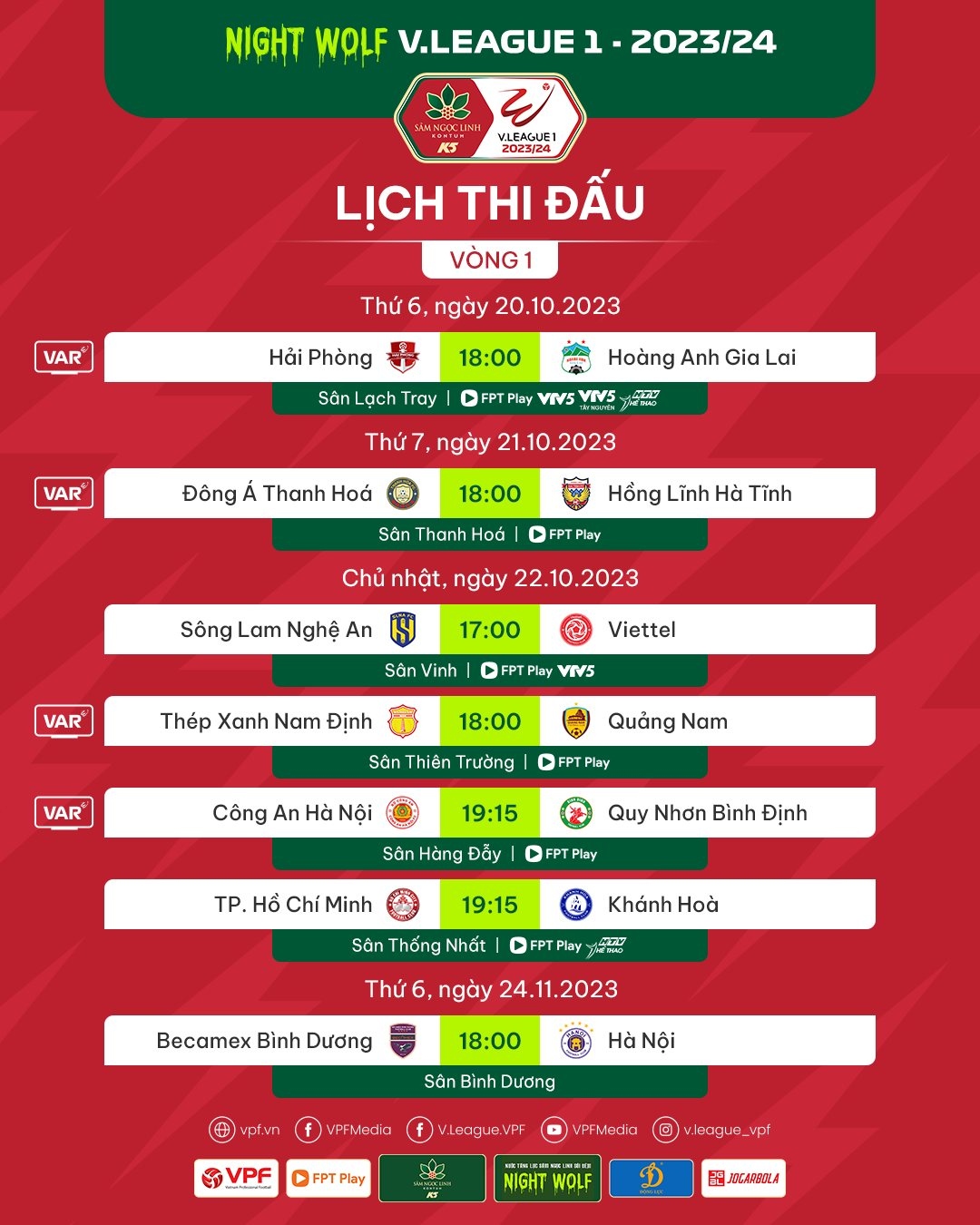
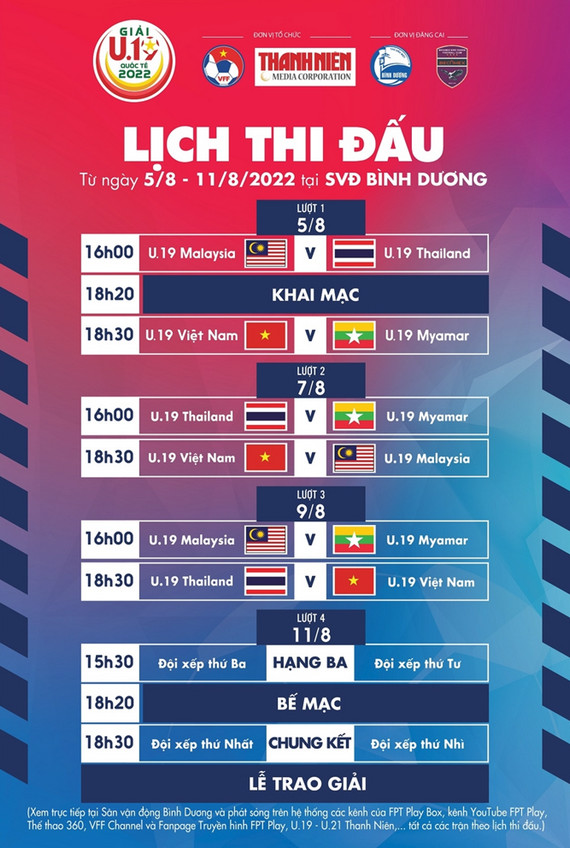
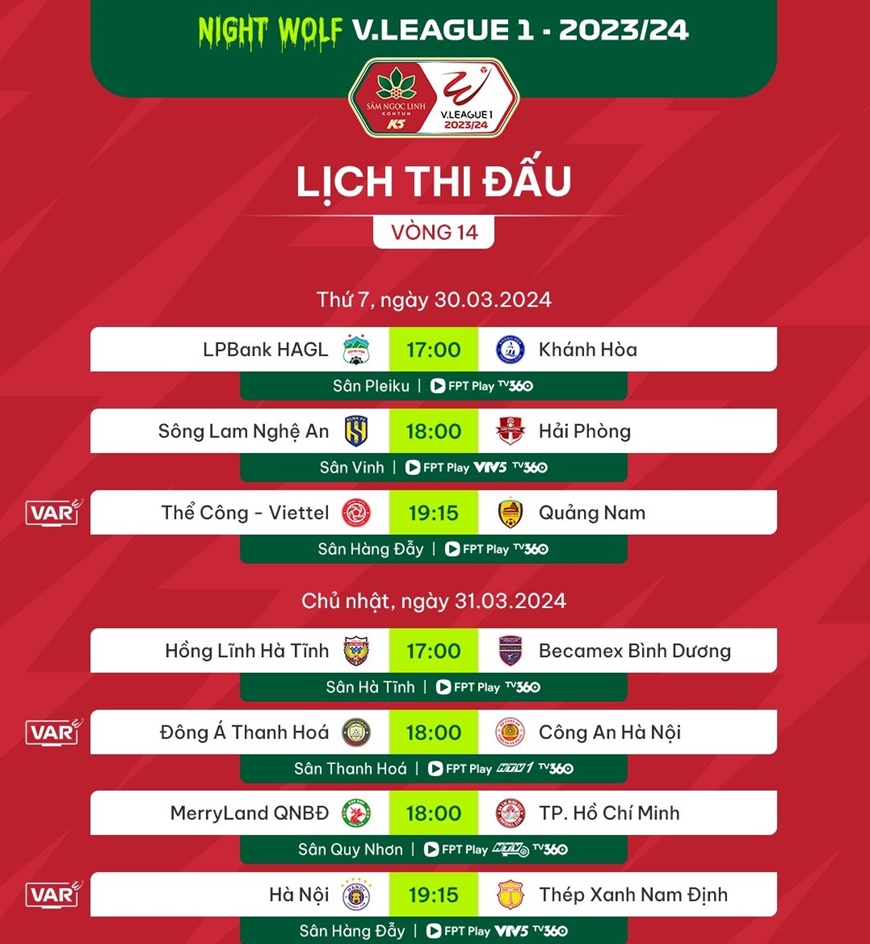
Lịch Thi Đấu
- Ngày 01/08/2024: Việt Nam vs Thái Lan - Giải Vô Địch Quốc Gia
- Ngày 02/08/2024: Việt Nam vs Malaysia - Vòng loại World Cup
- Ngày 03/08/2024: Việt Nam vs Indonesia - Giải AFF Cup
- Ngày 04/08/2024: Việt Nam vs Nga - Giao hữu quốc tế
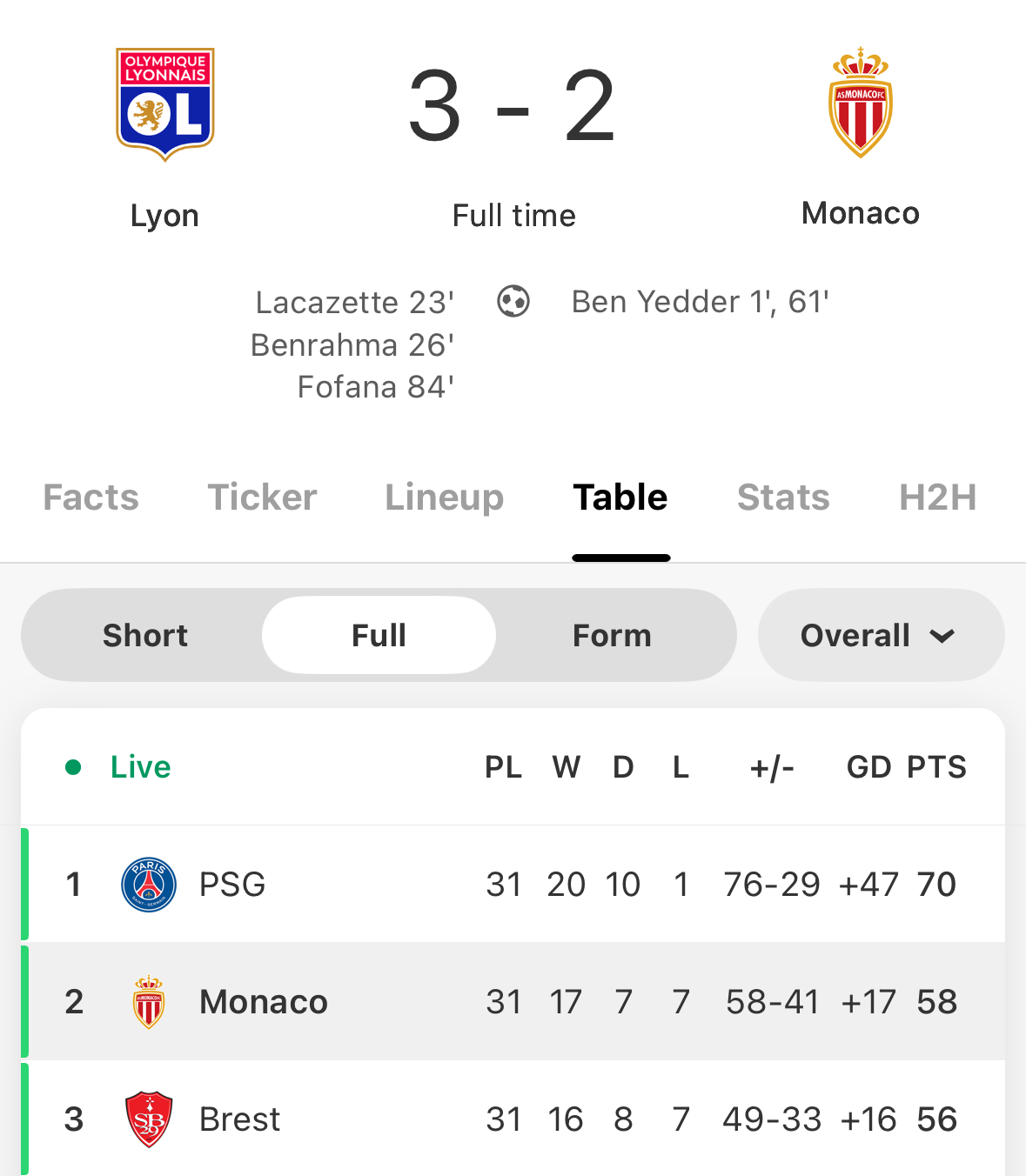
Kết Quả Các Trận Đấu Gần Đây
| Ngày | Trận Đấu | Kết Quả |
|---|---|---|
| 28/07/2024 | Việt Nam vs Thái Lan | 2 - 1 |
| 25/07/2024 | Việt Nam vs Malaysia | 1 - 0 |
| 21/07/2024 | Việt Nam vs Indonesia | 3 - 2 |
| 15/07/2024 | Việt Nam vs Philippines | 4 - 1 |
Các Giải Đấu Chính
- V.League: Giải đấu cấp cao nhất của Việt Nam với sự tham gia của các câu lạc bộ hàng đầu.
- Vòng loại World Cup: Đội tuyển Việt Nam thi đấu để giành vé tham dự World Cup.
- AFF Cup: Giải vô địch bóng đá Đông Nam Á, nơi Việt Nam thường là ứng cử viên nặng ký.
- Giao hữu quốc tế: Các trận đấu giao hữu với các đội tuyển quốc gia khác.
Tỷ lệ Kèo và Soi Kèo
Người hâm mộ có thể cập nhật thông tin tỷ lệ kèo mới nhất và các nhận định chuyên sâu về các trận đấu sắp tới để đưa ra những dự đoán chính xác.
Để theo dõi chi tiết hơn, vui lòng truy cập các trang web thể thao uy tín để nhận được thông tin cập nhật liên tục và chính xác nhất.

.png)
Mục lục tổng hợp thông tin về kết quả và lịch thi đấu bóng đá Việt Nam
Trang này cung cấp thông tin tổng hợp về kết quả và lịch thi đấu bóng đá Việt Nam, bao gồm các giải đấu quan trọng và các trận đấu nổi bật. Người hâm mộ có thể dễ dàng theo dõi các trận đấu của đội tuyển Việt Nam, các giải đấu trong nước cũng như quốc tế. Dưới đây là mục lục chi tiết:
- Lịch thi đấu bóng đá Việt Nam mới nhất: Thông tin chi tiết về lịch thi đấu của các giải đấu quốc nội và quốc tế có sự góp mặt của các đội tuyển Việt Nam, bao gồm cả đội tuyển quốc gia và các câu lạc bộ.
- Kết quả các trận đấu gần đây: Cập nhật kết quả các trận đấu đã diễn ra, bao gồm tỉ số, diễn biến chính và thông tin nổi bật.
- Tỷ lệ kèo và dự đoán kết quả: Thông tin về tỷ lệ kèo nhà cái, dự đoán kết quả trận đấu dựa trên phong độ hiện tại và lịch sử đối đầu của các đội bóng.
- Phân tích và bình luận sau trận đấu: Các bài phân tích chuyên sâu về diễn biến trận đấu, chiến thuật sử dụng, và các yếu tố quyết định kết quả cuối cùng.
- Danh sách cầu thủ và phong độ thi đấu: Thông tin về danh sách cầu thủ tham gia, tình hình chấn thương, phong độ hiện tại và những gương mặt nổi bật trong đội hình.
- Lịch sử đối đầu và thành tích thi đấu: Thống kê chi tiết về lịch sử đối đầu giữa các đội tuyển, thành tích đạt được tại các giải đấu trước đây.
- Tin tức chuyển nhượng và tình hình nội bộ: Cập nhật các thông tin chuyển nhượng cầu thủ, thay đổi trong ban huấn luyện và các tin tức nội bộ liên quan đến đội bóng.
- Nhận định trước trận đấu: Các dự đoán về kết quả trận đấu sắp tới dựa trên phân tích chuyên sâu, bao gồm các yếu tố như sân nhà, phong độ đội hình, và chiến thuật.
Hãy theo dõi để cập nhật những thông tin mới nhất về bóng đá Việt Nam và không bỏ lỡ bất kỳ trận đấu quan trọng nào!
Dạng bài tập Toán học: Giải phương trình bậc hai
Phương trình bậc hai là một trong những dạng phương trình cơ bản và quan trọng trong toán học. Dạng tổng quát của phương trình bậc hai có dạng:
Trong đó:
- \(a\), \(b\), \(c\) là các hệ số, với \(a \neq 0\).
- \(x\) là ẩn số cần tìm.
Để giải phương trình bậc hai, ta thực hiện các bước sau:
- Xác định các hệ số: Xác định giá trị của \(a\), \(b\), \(c\) từ phương trình.
- Tính biệt thức (delta): Tính giá trị của biệt thức theo công thức: \[ \Delta = b^2 - 4ac \]
- Xét dấu của biệt thức:
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm phân biệt được tính theo công thức: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép được tính theo công thức: \[ x = \frac{-b}{2a} \]
- Nếu \(\Delta < 0\): Phương trình vô nghiệm (không có nghiệm thực).
- Kết luận: Dựa vào giá trị của \(\Delta\) và các công thức trên, kết luận về nghiệm của phương trình.
Ví dụ: Giải phương trình \(2x^2 - 4x + 2 = 0\).
- Xác định các hệ số: \(a = 2\), \(b = -4\), \(c = 2\).
- Tính biệt thức: \[ \Delta = (-4)^2 - 4 \cdot 2 \cdot 2 = 16 - 16 = 0 \]
- Vì \(\Delta = 0\), phương trình có nghiệm kép: \[ x = \frac{-(-4)}{2 \cdot 2} = \frac{4}{4} = 1 \]
- Kết luận: Phương trình có nghiệm kép \(x = 1\).

Dạng bài tập Vật lý: Tính vận tốc trong chuyển động đều
Chuyển động đều là một dạng chuyển động mà vật di chuyển với vận tốc không đổi trên một quãng đường thẳng. Vận tốc trong chuyển động đều được tính bằng công thức cơ bản:
Trong đó:
- \(v\) là vận tốc của vật (đơn vị: m/s).
- \(s\) là quãng đường vật đã đi được (đơn vị: mét).
- \(t\) là thời gian vật di chuyển (đơn vị: giây).
Để giải bài tập tính vận tốc trong chuyển động đều, ta thực hiện các bước sau:
- Xác định các đại lượng đã biết: Xác định giá trị của quãng đường \(s\) và thời gian \(t\) từ đề bài.
- Áp dụng công thức: Sử dụng công thức \(v = \frac{s}{t}\) để tính vận tốc \(v\).
- Đơn vị tính: Đảm bảo các đại lượng \(s\) và \(t\) được sử dụng đúng đơn vị trước khi tính toán. Kết quả vận tốc sẽ có đơn vị là m/s.
- Kết luận: Đưa ra kết quả cuối cùng về vận tốc của vật.
Ví dụ: Một chiếc xe di chuyển quãng đường 100 mét trong thời gian 20 giây. Tính vận tốc của xe.
- Quãng đường \(s = 100\) mét.
- Thời gian \(t = 20\) giây.
- Vận tốc của xe được tính như sau: \[ v = \frac{100}{20} = 5 \, \text{m/s} \]
- Kết luận: Vận tốc của xe là 5 m/s.

Dạng bài tập Tiếng Anh: Sử dụng thì quá khứ đơn
Thì quá khứ đơn (Simple Past) là một trong những thì cơ bản và quan trọng trong tiếng Anh, thường được sử dụng để diễn tả một hành động đã xảy ra và kết thúc trong quá khứ. Công thức chung của thì quá khứ đơn là:
- Khẳng định: Chủ ngữ + Động từ quá khứ (V2) + (Tân ngữ)
- Phủ định: Chủ ngữ + did not + Động từ nguyên mẫu (V1) + (Tân ngữ)
- Nghi vấn: Did + Chủ ngữ + Động từ nguyên mẫu (V1) + (Tân ngữ)?
Để nắm vững thì quá khứ đơn, bạn cần thực hiện các bước sau:
- Xác định động từ: Động từ trong câu cần được chuyển sang dạng quá khứ, thường là thêm đuôi "-ed" với động từ có quy tắc, hoặc dạng bất quy tắc với các động từ không tuân theo quy tắc.
- Phân biệt cách sử dụng: Thì quá khứ đơn được dùng để diễn tả một hành động đã hoàn thành trong quá khứ. Ví dụ: "She visited her grandmother last weekend."
- Luyện tập qua ví dụ: Thực hiện các bài tập chuyển câu từ thì hiện tại đơn sang thì quá khứ đơn, và ngược lại để củng cố kiến thức.
- Phân biệt với các thì khác: Thì quá khứ đơn cần được phân biệt với thì hiện tại hoàn thành (Present Perfect) và thì quá khứ tiếp diễn (Past Continuous) để tránh nhầm lẫn khi sử dụng.
Ví dụ: Chuyển câu "He goes to school every day" sang thì quá khứ đơn.
- Câu đã chuyển: "He went to school yesterday."
- Phân tích: Động từ "goes" chuyển thành "went" để phù hợp với thì quá khứ đơn.

Dạng bài tập Toán học: Phân tích đa thức thành nhân tử
Phân tích đa thức thành nhân tử là một kỹ năng quan trọng trong toán học, giúp đơn giản hóa các biểu thức đại số và giải quyết các bài toán phức tạp. Phương pháp này dựa trên việc đưa một đa thức về tích của các nhân tử bậc thấp hơn. Dưới đây là các bước cơ bản để phân tích đa thức thành nhân tử:
- Tìm nhân tử chung: Nếu tất cả các hạng tử của đa thức đều có một nhân tử chung, hãy đặt nhân tử chung đó ra ngoài dấu ngoặc.
- Ví dụ: Với đa thức \(6x^3 + 9x^2\), nhân tử chung là \(3x^2\), ta có thể viết lại thành \(3x^2(2x + 3)\).
- Sử dụng hằng đẳng thức: Áp dụng các hằng đẳng thức để phân tích đa thức.
- Ví dụ: Sử dụng hằng đẳng thức \(a^2 - b^2 = (a - b)(a + b)\) để phân tích đa thức \(x^2 - 9\) thành \((x - 3)(x + 3)\).
- Nhóm các hạng tử: Khi đa thức có nhiều hơn ba hạng tử, ta có thể nhóm các hạng tử sao cho chúng có nhân tử chung.
- Ví dụ: Đa thức \(x^3 - x^2 + 2x - 2\) có thể được nhóm thành \((x^2(x - 1) + 2(x - 1))\) và sau đó là \((x^2 + 2)(x - 1)\).
- Phương pháp tách hạng tử: Với các đa thức bậc hai, phương pháp tách hạng tử có thể được áp dụng để tìm các nhân tử.
- Ví dụ: Đối với phương trình \(x^2 + 5x + 6\), ta có thể tách thành \(x^2 + 2x + 3x + 6\), rồi phân tích thành \((x + 2)(x + 3)\).
- Sử dụng nghiệm của phương trình: Nếu biết nghiệm của phương trình, ta có thể phân tích đa thức tương ứng thành nhân tử.
- Ví dụ: Nếu phương trình \(x^2 - 5x + 6 = 0\) có nghiệm là \(x = 2\) và \(x = 3\), ta có thể phân tích thành \( (x - 2)(x - 3)\).
Phân tích đa thức thành nhân tử là một kỹ năng cần thiết trong toán học, giúp đơn giản hóa các bài toán và dễ dàng tìm ra các nghiệm của phương trình.
XEM THÊM:
Dạng bài tập Vật lý: Định luật Bảo toàn năng lượng
Định luật Bảo toàn năng lượng là một trong những nguyên lý cơ bản trong vật lý học, phát biểu rằng năng lượng không tự sinh ra hay mất đi, mà chỉ chuyển từ dạng này sang dạng khác hoặc truyền từ vật này sang vật khác. Dạng bài tập liên quan đến định luật này thường yêu cầu học sinh tính toán sự biến đổi năng lượng trong các hệ vật lý. Dưới đây là các bước cụ thể để giải quyết bài tập liên quan đến định luật Bảo toàn năng lượng.
-
Xác định hệ thống cần phân tích:
Trước tiên, bạn cần xác định rõ hệ thống đang xét, bao gồm các vật thể tham gia và các loại năng lượng liên quan như thế năng, động năng, nhiệt năng, v.v.
-
Viết biểu thức năng lượng ban đầu và năng lượng cuối cùng:
Sử dụng các công thức tương ứng cho từng loại năng lượng, bạn sẽ viết biểu thức tổng quát cho năng lượng ban đầu và năng lượng cuối cùng của hệ thống.
- Thế năng: \[ E_{\text{thế}} = mgh \]
- Động năng: \[ E_{\text{động}} = \frac{1}{2}mv^2 \]
-
Áp dụng định luật Bảo toàn năng lượng:
Theo định luật Bảo toàn năng lượng, năng lượng ban đầu bằng năng lượng cuối cùng:
\[ E_{\text{ban đầu}} = E_{\text{cuối cùng}} \]
Từ đó, bạn có thể thiết lập phương trình để giải các đại lượng cần tìm.
-
Giải phương trình:
Sau khi có phương trình, bạn giải phương trình này để tìm các giá trị chưa biết như vận tốc, độ cao, hay các thông số khác tùy thuộc vào yêu cầu của bài tập.
-
Kết luận và kiểm tra kết quả:
Cuối cùng, hãy kiểm tra lại kết quả để đảm bảo tính hợp lý và phù hợp với các điều kiện ban đầu của bài toán. Đảm bảo rằng kết quả thỏa mãn định luật Bảo toàn năng lượng.
Dưới đây là một ví dụ cụ thể:
Bài toán: Một vật có khối lượng \( m = 2 \, \text{kg} \) rơi từ độ cao \( h = 10 \, \text{m} \). Tính vận tốc của vật ngay trước khi chạm đất. Bỏ qua sức cản không khí.
Giải:
- Xác định hệ thống và năng lượng liên quan:
- Năng lượng ban đầu là thế năng: \[ E_{\text{thế}} = mgh = 2 \times 9.8 \times 10 = 196 \, \text{J} \]
- Năng lượng cuối cùng là động năng: \[ E_{\text{động}} = \frac{1}{2}mv^2 \]
- Áp dụng định luật Bảo toàn năng lượng:
\[ mgh = \frac{1}{2}mv^2 \]
- Giải phương trình để tìm vận tốc \( v \):
\[ 196 = \frac{1}{2} \times 2 \times v^2 \]
\[ v^2 = 196 \]
\[ v = \sqrt{196} \approx 14 \, \text{m/s} \]
- Kết luận: Vận tốc của vật ngay trước khi chạm đất là \( v \approx 14 \, \text{m/s} \).
Dạng bài tập Tiếng Anh: Viết lại câu sử dụng câu điều kiện loại 1
Trong Tiếng Anh, câu điều kiện loại 1 (First Conditional) được sử dụng để nói về những sự việc có khả năng xảy ra trong tương lai nếu một điều kiện cụ thể được đáp ứng. Dưới đây là một số bước chi tiết và ví dụ để giúp bạn viết lại câu sử dụng câu điều kiện loại 1.
Bước 1: Cấu trúc câu điều kiện loại 1
- Điều kiện: If + S + V (hiện tại đơn)
- Kết quả: S + will + V (nguyên thể)
Ví dụ: If it rains, we will stay at home.
Bước 2: Chuyển câu từ thì hiện tại sang câu điều kiện loại 1
Để viết lại câu, bạn cần xác định điều kiện và kết quả có thể xảy ra trong tương lai. Sau đó, áp dụng cấu trúc của câu điều kiện loại 1.
Ví dụ:
- Câu gốc: You study hard. You pass the exam.
Câu điều kiện loại 1: If you study hard, you will pass the exam. - Câu gốc: He comes early. We go to the cinema.
Câu điều kiện loại 1: If he comes early, we will go to the cinema. - Câu gốc: She finishes her homework. She can watch TV.
Câu điều kiện loại 1: If she finishes her homework, she will be able to watch TV.
Bước 3: Luyện tập thêm
Hãy thử viết lại các câu sau sử dụng câu điều kiện loại 1:
- It gets colder. We wear warmer clothes.
- You work hard. You get a promotion.
- They arrive on time. We start the meeting.
Bảng động từ thường sử dụng trong câu điều kiện loại 1:
| Động từ | Dạng hiện tại | Dạng tương lai (will + V) |
|---|---|---|
| Study | Study | Will study |
| Come | Come | Will come |
| Finish | Finish | Will finish |
| Go | Go | Will go |
| Get | Get | Will get |

Dạng bài tập Toán học: Giải hệ phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn là một dạng bài toán cơ bản trong chương trình Toán học cấp trung học. Dưới đây là hướng dẫn chi tiết cách giải một hệ phương trình bậc nhất hai ẩn:
- Bước 1: Viết hệ phương trình dạng tổng quát: \[ \begin{cases} a_1 x + b_1 y = c_1 \\ a_2 x + b_2 y = c_2 \end{cases} \] Trong đó: \( a_1, a_2, b_1, b_2, c_1, c_2 \) là các hằng số đã biết, và \( x, y \) là ẩn số cần tìm.
- Bước 2: Phương pháp thế:
- Giải phương trình thứ nhất theo một ẩn (ví dụ: \( x \)): \[ x = \frac{c_1 - b_1 y}{a_1} \]
- Thế giá trị \( x \) vào phương trình thứ hai để tìm ẩn \( y \): \[ a_2 \left( \frac{c_1 - b_1 y}{a_1} \right) + b_2 y = c_2 \]
- Giải phương trình trên để tìm \( y \).
- Sau khi tìm được \( y \), thế ngược lại vào phương trình đã giải ở bước đầu để tìm \( x \).
- Bước 3: Phương pháp cộng đại số:
- Nhân các phương trình với các hệ số phù hợp để các ẩn số có cùng hệ số, rồi trừ (hoặc cộng) hai phương trình để khử một ẩn.
- Giải phương trình còn lại để tìm giá trị của ẩn kia.
- Thế giá trị vừa tìm được vào một trong các phương trình ban đầu để tìm giá trị của ẩn còn lại.
- Bước 4: Kiểm tra lại kết quả bằng cách thay các giá trị của \( x \) và \( y \) vào cả hai phương trình ban đầu.
Ví dụ: Giải hệ phương trình sau:
\[
\begin{cases}
2x + 3y = 7 \\
4x - y = 5
\end{cases}
\]
- Giải phương trình thứ nhất theo \( x \): \[ x = \frac{7 - 3y}{2} \]
- Thế giá trị này vào phương trình thứ hai: \[ 4 \left( \frac{7 - 3y}{2} \right) - y = 5 \] Sau khi giải phương trình, ta tìm được \( y = 1 \).
- Thế \( y = 1 \) vào phương trình thứ nhất: \[ 2x + 3(1) = 7 \quad \Rightarrow \quad 2x = 4 \quad \Rightarrow \quad x = 2 \]
Kết quả: Hệ phương trình có nghiệm là \( x = 2 \) và \( y = 1 \).
Giải hệ phương trình bậc nhất hai ẩn không chỉ là kỹ năng cơ bản mà còn là nền tảng quan trọng trong các bài toán phức tạp hơn trong tương lai.
Dạng bài tập Vật lý: Tính lực trong các hệ cân bằng
Trong vật lý, hệ cân bằng là một hệ trong đó tổng hợp lực tác động lên các vật bằng không, dẫn đến trạng thái nghỉ hoặc chuyển động đều. Để tính lực trong các hệ cân bằng, ta áp dụng điều kiện cân bằng của vật rắn: tổng các lực và tổng các mô men tác dụng lên vật phải bằng 0.
Ví dụ, xét một hệ gồm một thanh ngang dài \( L \) được đặt trên hai điểm tựa \( A \) và \( B \). Trên thanh tác dụng lực \( F_1 \) tại điểm cách \( A \) một khoảng \( d_1 \) và lực \( F_2 \) tại điểm cách \( B \) một khoảng \( d_2 \).
Công thức tính lực trong hệ cân bằng:
- Điều kiện cân bằng về lực: \[ \sum F = 0 \quad \Rightarrow \quad F_1 + F_2 = F_3 + F_4 \]
- Điều kiện cân bằng về mô men: \[ \sum M = 0 \quad \Rightarrow \quad F_1 \cdot d_1 = F_2 \cdot d_2 \]
Để giải quyết bài toán, hãy làm theo các bước sau:
- Xác định tất cả các lực tác dụng lên hệ.
- Chọn một điểm để tính mô men (thường là một trong các điểm tựa).
- Áp dụng các điều kiện cân bằng lực và cân bằng mô men để thiết lập phương trình.
- Giải các phương trình để tìm các lực chưa biết.
Ví dụ thực hành:
Xét một thanh ngang dài 4m đặt trên hai điểm tựa \( A \) và \( B \) cách nhau 3m. Tại điểm cách \( A \) 1m, tác dụng một lực \( F_1 = 200 \, N \). Tại điểm cách \( B \) 2m, tác dụng một lực \( F_2 = 150 \, N \). Tìm các lực tác dụng lên điểm tựa \( A \) và \( B \).
Áp dụng điều kiện cân bằng lực:
\[
F_A + F_B = F_1 + F_2 = 200 + 150 = 350 \, N
\]
Áp dụng điều kiện cân bằng mô men quanh điểm \( A \):
\[
F_B \cdot 3 = 200 \cdot 1 + 150 \cdot 2 = 200 + 300 = 500 \, N \cdot m
\quad \Rightarrow \quad F_B = \frac{500}{3} \approx 166.67 \, N
\]
Thay vào phương trình cân bằng lực:
\[
F_A = 350 - 166.67 = 183.33 \, N
\]
Kết quả: Lực tác dụng lên điểm tựa \( A \) là \( 183.33 \, N \), và lên điểm tựa \( B \) là \( 166.67 \, N \).

Dạng bài tập Tiếng Anh: Hoàn thành câu với từ cho trước
Trong dạng bài tập này, học sinh sẽ được cung cấp các từ hoặc cụm từ và phải hoàn thành câu sao cho hợp lý và đúng ngữ pháp. Đây là một dạng bài tập phổ biến giúp củng cố kiến thức ngữ pháp, từ vựng, và kỹ năng viết câu.
Các bước thực hiện:
- Đọc kỹ yêu cầu đề bài: Xem xét kỹ từ hoặc cụm từ được cung cấp và xác định cách thức mà chúng cần được sử dụng trong câu.
- Xác định thì của câu: Dựa trên ngữ cảnh, xác định thì của câu và chỉnh sửa động từ hoặc cấu trúc câu cho phù hợp.
- Hoàn thiện câu: Sau khi xác định được cấu trúc ngữ pháp và ngữ nghĩa cần thiết, học sinh sẽ điền từ hoặc cụm từ được cho vào vị trí thích hợp trong câu.
Ví dụ:
Hoàn thành các câu dưới đây với từ được cho trong ngoặc:
- She will call you if she _____ (get) home early.
- If it _____ (rain) tomorrow, we will cancel the trip.
- We will go out for dinner if he _____ (finish) his work on time.
- They _____ (not come) to the party if they are too tired.
Đáp án tham khảo:
- She will call you if she gets home early.
- If it rains tomorrow, we will cancel the trip.
- We will go out for dinner if he finishes his work on time.
- They will not come to the party if they are too tired.
Những lưu ý:
- Cần chú ý tới động từ trong câu điều kiện loại 1, thường sử dụng thì hiện tại đơn ở mệnh đề điều kiện (if) và thì tương lai đơn ở mệnh đề chính.
- Câu điều kiện loại 1 được sử dụng để nói về những sự việc có khả năng xảy ra trong tương lai nếu điều kiện được đáp ứng.
Qua các bài tập này, học sinh sẽ nắm vững hơn về cấu trúc câu điều kiện loại 1 và cách sử dụng trong giao tiếp hàng ngày.
Dạng bài tập Toán học: Giải phương trình vô tỉ
Phương trình vô tỉ là những phương trình có chứa ẩn số dưới dấu căn. Để giải loại phương trình này, ta cần biến đổi sao cho loại bỏ được dấu căn và giải phương trình còn lại. Dưới đây là các bước cơ bản để giải một phương trình vô tỉ.
- Bước 1: Phân tích và xác định điều kiện xác định của phương trình. Điều kiện xác định là những giá trị của biến mà biểu thức dưới dấu căn phải không âm.
- Bước 2: Bình phương hai vế của phương trình để loại bỏ dấu căn.
- Bước 3: Giải phương trình vừa thu được sau khi bình phương.
- Bước 4: Kiểm tra lại điều kiện xác định.
Ví dụ: Với phương trình \(\sqrt{x - 1} = 2\), điều kiện là \(x - 1 \geq 0\), tức là \(x \geq 1\).
Bình phương hai vế của phương trình vô tỉ sẽ giúp loại bỏ căn bậc hai. Ví dụ, với phương trình \(\sqrt{x - 1} = 2\), ta bình phương hai vế được:
\[ (\sqrt{x - 1})^2 = 2^2 \quad \Rightarrow \quad x - 1 = 4 \]Từ phương trình \(x - 1 = 4\), ta giải được:
\[ x = 4 + 1 = 5 \]Cuối cùng, ta kiểm tra lại nghiệm vừa tìm được có thỏa mãn điều kiện xác định ban đầu hay không. Với \(x = 5\), ta thấy \(x \geq 1\), do đó nghiệm này thỏa mãn điều kiện và là nghiệm đúng của phương trình.
Như vậy, nghiệm của phương trình là \(x = 5\).
Lưu ý: Đối với một số phương trình vô tỉ phức tạp hơn, sau khi bình phương có thể dẫn tới phương trình bậc hai hoặc bậc cao hơn. Trong những trường hợp này, cần sử dụng các phương pháp giải phương trình thích hợp như nhân phân tích, nghiệm thử, hoặc các công thức giải phương trình bậc hai.
Ví dụ khác:
Giải phương trình \(\sqrt{2x + 3} = x + 1\).
- Bước 1: Điều kiện xác định: \(2x + 3 \geq 0\), tức là \(x \geq -\frac{3}{2}\).
- Bước 2: Bình phương hai vế: \[ (\sqrt{2x + 3})^2 = (x + 1)^2 \quad \Rightarrow \quad 2x + 3 = x^2 + 2x + 1 \]
- Bước 3: Giải phương trình bậc hai: \[ x^2 + 2x + 1 - 2x - 3 = 0 \quad \Rightarrow \quad x^2 - 2 = 0 \quad \Rightarrow \quad x = \pm\sqrt{2} \]
- Bước 4: Kiểm tra điều kiện xác định:
Với \(x = \sqrt{2}\), nghiệm thỏa mãn điều kiện \(x \geq -\frac{3}{2}\).
Với \(x = -\sqrt{2}\), nghiệm không thỏa mãn điều kiện \(x \geq -\frac{3}{2}\).
Kết luận: Nghiệm của phương trình là \(x = \sqrt{2}\).