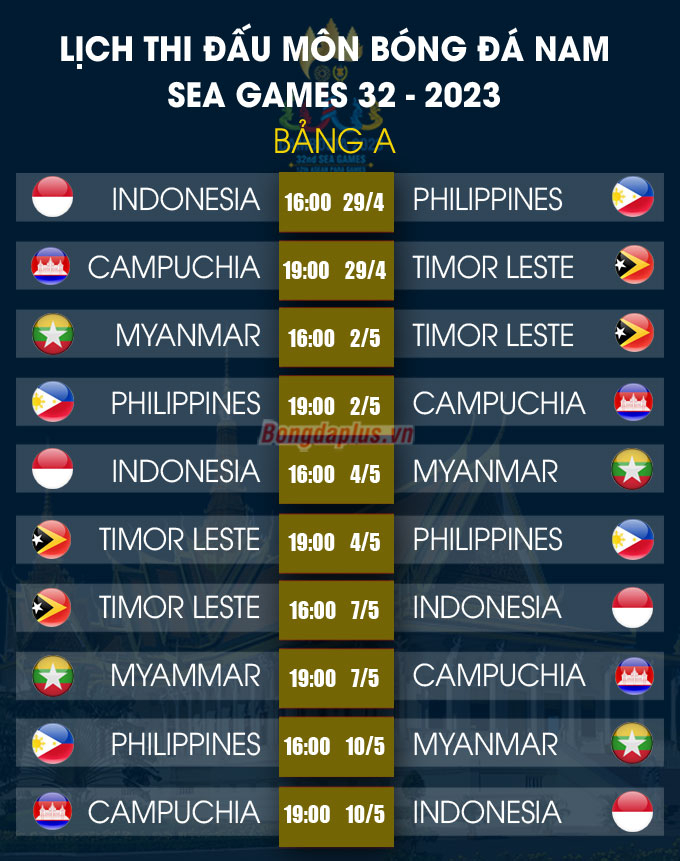
Chủ đề lịch thi đấu bóng đá 4/8: Lịch thi đấu bóng đá ngày 4/8 hứa hẹn sẽ mang đến cho người hâm mộ những trận cầu kịch tính từ các giải đấu lớn như Europa League, Vô Địch Quốc Gia Thụy Điển, và nhiều giải đấu hấp dẫn khác. Cùng khám phá chi tiết lịch thi đấu và đừng bỏ lỡ bất kỳ cuộc đối đầu đỉnh cao nào!
Mục lục
- Lịch Thi Đấu Bóng Đá Ngày 4/8
- Mục Lục Tổng Hợp Lịch Thi Đấu Bóng Đá Ngày 4/8
- Bài Tập Toán: Giải Hệ Phương Trình
- Bài Tập Lý: Tính Toán Điện Trở Tổng
- Bài Tập Tiếng Anh: Hoàn Thành Câu Sử Dụng Thì Hiện Tại Hoàn Thành
- Bài Tập Toán: Tính Tích Phân
- Bài Tập Lý: Phân Tích Chuyển Động Ném Ngang
- Bài Tập Tiếng Anh: Chọn Đáp Án Đúng Trong Các Câu Điều Kiện
- Bài Tập Toán: Giải Bất Phương Trình Bậc Hai
- Bài Tập Lý: Tính Lực Ma Sát
- Bài Tập Tiếng Anh: Sắp Xếp Từ Thành Câu Hoàn Chỉnh
- Bài Tập Toán: Tính Xác Suất
Lịch Thi Đấu Bóng Đá Ngày 4/8
Dưới đây là thông tin chi tiết về lịch thi đấu bóng đá ngày 4/8 từ nhiều giải đấu quốc tế và quốc gia:
1. Giải Vô Địch Quốc Gia Thụy Điển
- 19:00 - Värnamo vs Sirius
- 21:30 - Kalmar vs Hammarby
2. Giải Vô Địch Quốc Gia Thụy Sĩ
- 19:15 - Lausanne vs St.Gallen
- 21:30 - Winterthur vs Yverdon
- 21:30 - Young Boys vs Zürich
3. Giải Vô Địch Quốc Gia Uruguay
- 01:00 (5/8) - Nacional vs Peñarol
4. Europa League
- 22:30 - AEK Larnaca vs Partizan
- 00:00 (5/8) - Malmö vs F91 Dudelange
- 00:00 (5/8) - Fenerbahce vs Slovacko
- 01:15 (5/8) - Maribor vs HJK
- 01:45 (5/8) - Linfield vs Zürich
- 02:00 (5/8) - Shamrock Rovers vs Shkupi
- 02:00 (5/8) - Olympiakos vs Slovan Bratislava
5. Europa Conference League
- 23:00 - Rigas FS vs Hibernians
- 23:00 - KuPS vs Young Boys
- 23:30 - Spartak Trnava vs Rakow Czestochowa
- 23:45 - Paide vs Anderlecht
- 00:00 (5/8) - CSKA Sofia vs St Patrick's Athletic
- 00:00 (5/8) - AIK vs Shkendija
- 00:00 (5/8) - APOEL vs Kyzyl-Zhar
- 00:00 (5/8) - Maccabi Tel Aviv vs Aris
- 00:00 (5/8) - Lillestrøm vs Antwerp
- 00:00 (5/8) - Neftchi Baku vs Rapid Vienna
- 00:00 (5/8) - Shakhtyor vs CFR Cluj
- 00:00 (5/8) - Slavia Prague vs Panathinaikos
- 00:00 (5/8) - Molde vs Kisvárda
- 00:00 (5/8) - Viking vs Sligo Rovers
- 00:30 (5/8) - Zorya vs Universitatea Craiova
- 01:00 (5/8) - Lugano vs Hapoel Be'er Sheva
- 01:00 (5/8) - Cukaricki vs Twente
- 01:00 (5/8) - Hamrun Spartans vs Levski Sofia
- 01:00 (5/8) - Ballkani vs KÍ
- 01:00 (5/8) - Sepsi vs Djurgården
- 01:00 (5/8) - Vaduz vs Konyaspor
- 01:30 (5/8) - Brøndby vs Basel
- 01:45 (5/8) - Víkingur Reykjavík vs Lech Poznań
Đây là danh sách các trận đấu sẽ diễn ra vào ngày 4/8 từ các giải đấu hàng đầu châu Âu và Nam Mỹ. Các trận đấu này sẽ được cập nhật liên tục để người hâm mộ không bỏ lỡ bất kỳ trận cầu hấp dẫn nào.

.png)
Mục Lục Tổng Hợp Lịch Thi Đấu Bóng Đá Ngày 4/8
-
1. Lịch Thi Đấu Giải Vô Địch Quốc Gia Thụy Điển
- 19:00 - Värnamo vs Sirius
- 21:30 - Kalmar vs Hammarby
-
2. Lịch Thi Đấu Giải Vô Địch Quốc Gia Thụy Sĩ
- 19:15 - Lausanne vs St.Gallen
- 21:30 - Winterthur vs Yverdon
- 21:30 - Young Boys vs Zürich
-
3. Lịch Thi Đấu Giải Vô Địch Quốc Gia Uruguay
- 01:00 (5/8) - Nacional vs Peñarol
-
4. Lịch Thi Đấu Europa League Ngày 4/8
- 22:30 - AEK Larnaca vs Partizan
- 00:00 (5/8) - Malmö vs F91 Dudelange
- 00:00 (5/8) - Fenerbahce vs Slovacko
- 01:15 (5/8) - Maribor vs HJK
- 01:45 (5/8) - Linfield vs Zürich
- 02:00 (5/8) - Shamrock Rovers vs Shkupi
- 02:00 (5/8) - Olympiakos vs Slovan Bratislava
-
5. Lịch Thi Đấu Europa Conference League Ngày 4/8
- 23:00 - Rigas FS vs Hibernians
- 23:00 - KuPS vs Young Boys
- 23:30 - Spartak Trnava vs Rakow Czestochowa
- 23:45 - Paide vs Anderlecht
- 00:00 (5/8) - CSKA Sofia vs St Patrick's Athletic
- 00:00 (5/8) - AIK vs Shkendija
- 00:00 (5/8) - APOEL vs Kyzyl-Zhar
- 00:00 (5/8) - Maccabi Tel Aviv vs Aris
- 00:00 (5/8) - Lillestrøm vs Antwerp
- 00:00 (5/8) - Neftchi Baku vs Rapid Vienna
- 00:00 (5/8) - Shakhtyor vs CFR Cluj
- 00:00 (5/8) - Slavia Prague vs Panathinaikos
- 00:00 (5/8) - Molde vs Kisvárda
- 00:00 (5/8) - Viking vs Sligo Rovers
- 00:30 (5/8) - Zorya vs Universitatea Craiova
- 01:00 (5/8) - Lugano vs Hapoel Be'er Sheva
- 01:00 (5/8) - Cukaricki vs Twente
- 01:00 (5/8) - Hamrun Spartans vs Levski Sofia
- 01:00 (5/8) - Ballkani vs KÍ
- 01:00 (5/8) - Sepsi vs Djurgården
- 01:00 (5/8) - Vaduz vs Konyaspor
- 01:30 (5/8) - Brøndby vs Basel
- 01:45 (5/8) - Víkingur Reykjavík vs Lech Poznań
-
6. Lịch Thi Đấu Giải Bóng Đá U16 Đông Nam Á
- 16:00 - Thái Lan U16 vs Philippines U16
- 19:00 - Indonesia U16 vs Singapore U16
-
7. Lịch Thi Đấu Giải Cúp Nam Mỹ Ngày 4/8
- 05:00 - Internacional vs Colo Colo
- 07:30 - Fortaleza vs Estudiantes
-
8. Lịch Thi Đấu Giải Vô Địch Quốc Gia Brazil
- 02:00 (5/8) - Botafogo vs Ceará
- 02:00 (5/8) - Juventude vs América-MG
-
9. Lịch Thi Đấu Giải Vô Địch Quốc Gia Argentina
- 05:00 - Racing Club vs Arsenal Sarandí
- 07:15 - Platense vs Central Córdoba
-
10. Lịch Thi Đấu Giao Hữu Quốc Tế Ngày 4/8
- 20:00 - Ajax vs Celtic
- 21:30 - PSG vs Kawasaki Frontale
Bài Tập Toán: Giải Hệ Phương Trình
Trong bài tập này, chúng ta sẽ giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số. Bài toán yêu cầu tìm nghiệm của hệ phương trình sau:
- Bước 1: Giải phương trình thứ hai theo \(y\).
Ta có phương trình:
\[ 4x - y = 1 \Rightarrow y = 4x - 1 \] - Bước 2: Thế giá trị của \(y\) vào phương trình thứ nhất.
Ta thay \(y = 4x - 1\) vào phương trình thứ nhất:
\[ 2x + 3(4x - 1) = 7 \]Sau khi nhân và thu gọn, ta được:
\[ 2x + 12x - 3 = 7 \Rightarrow 14x = 10 \Rightarrow x = \frac{5}{7} \] - Bước 3: Tìm giá trị của \(y\) bằng cách thay giá trị \(x\) vào phương trình đã giải theo \(y\).
Ta có:
\[ y = 4x - 1 = 4\left(\frac{5}{7}\right) - 1 = \frac{20}{7} - \frac{7}{7} = \frac{13}{7} \] - Kết luận: Vậy nghiệm của hệ phương trình là: \[ x = \frac{5}{7}, y = \frac{13}{7} \]
Đây là cách giải hệ phương trình cơ bản, phù hợp cho các bài toán yêu cầu tìm nghiệm chính xác. Chúc các bạn luyện tập và nắm vững phương pháp này!

Bài Tập Lý: Tính Toán Điện Trở Tổng
Trong bài tập này, chúng ta sẽ tính toán điện trở tổng của một mạch điện với các điện trở mắc nối tiếp và song song. Bài toán được mô tả như sau:
Giả sử chúng ta có ba điện trở \(R_1\), \(R_2\), và \(R_3\) được mắc trong mạch như sau:
- Điện trở \(R_1 = 2 \, \Omega\) mắc nối tiếp với điện trở \(R_2 = 3 \, \Omega\).
- Điện trở \(R_3 = 6 \, \Omega\) mắc song song với tổ hợp \(R_1\) và \(R_2\).
Yêu cầu: Tính điện trở tổng \(R_{tổng}\) của mạch điện.
- Bước 1: Tính điện trở tương đương của \(R_1\) và \(R_2\) mắc nối tiếp.
Điện trở tương đương \(R_{12}\) của hai điện trở mắc nối tiếp được tính bằng:
\[ R_{12} = R_1 + R_2 = 2 \, \Omega + 3 \, \Omega = 5 \, \Omega \] - Bước 2: Tính điện trở tổng \(R_{tổng}\) của mạch với \(R_{12}\) mắc song song với \(R_3\).
Điện trở tổng của hai điện trở mắc song song được tính bằng:
\[ \frac{1}{R_{tổng}} = \frac{1}{R_{12}} + \frac{1}{R_3} = \frac{1}{5 \, \Omega} + \frac{1}{6 \, \Omega} \]Tiếp tục tính toán:
\[ \frac{1}{R_{tổng}} = \frac{6 + 5}{30} = \frac{11}{30} \]Suy ra:
\[ R_{tổng} = \frac{30}{11} \approx 2.73 \, \Omega \] - Kết luận: Điện trở tổng của mạch là: \[ R_{tổng} \approx 2.73 \, \Omega \]
Bài tập trên giúp chúng ta hiểu cách tính toán điện trở tổng của một mạch điện có các điện trở mắc nối tiếp và song song. Đây là một dạng bài tập cơ bản trong vật lý điện học, giúp củng cố kiến thức về nguyên lý mắc điện trở.

Bài Tập Tiếng Anh: Hoàn Thành Câu Sử Dụng Thì Hiện Tại Hoàn Thành
Trong bài tập này, chúng ta sẽ thực hành hoàn thành các câu sử dụng thì hiện tại hoàn thành. Đây là thì dùng để diễn tả một hành động đã hoàn thành tại một thời điểm không xác định trong quá khứ và vẫn còn ảnh hưởng đến hiện tại.
- Bước 1: Xem xét câu cần hoàn thành và xác định động từ chính.
Ví dụ: I ______ (visit) Paris three times.
- Bước 2: Sử dụng cấu trúc của thì hiện tại hoàn thành:
have/has + V(past participle)
Ví dụ: I have visited Paris three times.
- Bước 3: Hoàn thành câu với dạng đúng của động từ.
Ví dụ: She ______ (finish) her homework.
Sau khi áp dụng công thức: She has finished her homework.
- Bước 4: Kiểm tra lại câu để đảm bảo sử dụng đúng thì.
Chúng ta cũng cần xem xét các từ chỉ thời gian phù hợp với thì hiện tại hoàn thành như "ever," "never," "already," "yet," và "just".
Việc luyện tập với thì hiện tại hoàn thành giúp bạn làm chủ cấu trúc câu phức tạp hơn trong tiếng Anh, từ đó cải thiện kỹ năng giao tiếp và viết một cách tự nhiên hơn.

Bài Tập Toán: Tính Tích Phân
Trong bài tập này, chúng ta sẽ tính tích phân của một hàm số cụ thể trong khoảng cho trước. Bài toán được mô tả như sau:
Giả sử chúng ta cần tính tích phân của hàm số \(f(x) = x^2 + 2x + 1\) trong khoảng từ \(x = 0\) đến \(x = 2\).
- Bước 1: Xác định hàm số cần tính tích phân.
Hàm số cần tính tích phân là \(f(x) = x^2 + 2x + 1\).
- Bước 2: Viết công thức tích phân cần tính.
Công thức tích phân xác định là:
\[ \int_{0}^{2} (x^2 + 2x + 1) \, dx \] - Bước 3: Tính nguyên hàm của hàm số.
Nguyên hàm của \(f(x)\) là:
\[ \int (x^2 + 2x + 1) \, dx = \frac{x^3}{3} + x^2 + x + C \]Với \(C\) là hằng số tích phân.
- Bước 4: Thay cận vào để tính giá trị tích phân.
Chúng ta tính giá trị tích phân bằng cách thay cận:
\[ \left[ \frac{x^3}{3} + x^2 + x \right]_{0}^{2} = \left( \frac{2^3}{3} + 2^2 + 2 \right) - \left( \frac{0^3}{3} + 0^2 + 0 \right) \]Tiếp tục tính toán:
\[ \frac{8}{3} + 4 + 2 = \frac{8}{3} + \frac{12}{3} + \frac{6}{3} = \frac{26}{3} \] - Kết luận: Giá trị của tích phân là: \[ \int_{0}^{2} (x^2 + 2x + 1) \, dx = \frac{26}{3} \]
Bài tập này giúp chúng ta củng cố kiến thức về tính tích phân của hàm số, một công cụ quan trọng trong toán học để tính diện tích dưới đường cong, tổng đại số, và nhiều ứng dụng khác.
XEM THÊM:
Bài Tập Lý: Phân Tích Chuyển Động Ném Ngang
Chuyển động ném ngang là một dạng chuyển động của vật thể khi nó được phóng ngang với vận tốc ban đầu \(v_0\) từ một độ cao nhất định so với mặt đất. Chuyển động này có thể được phân tích thành hai chuyển động độc lập: chuyển động ngang đều và chuyển động rơi tự do.
1. Phân tích chuyển động theo phương ngang:
Vì không có lực tác động theo phương ngang (nếu bỏ qua lực cản của không khí), vận tốc theo phương ngang sẽ không đổi:
- Vận tốc theo phương ngang: \(v_x = v_0\)
- Quãng đường đi được theo phương ngang sau thời gian \(t\): \(x = v_0 \cdot t\)
2. Phân tích chuyển động theo phương thẳng đứng:
Theo phương thẳng đứng, vật chịu tác dụng của trọng lực \(g\), nên nó sẽ rơi tự do với gia tốc \(g\). Lúc này, ta có:
- Vận tốc theo phương thẳng đứng sau thời gian \(t\): \(v_y = g \cdot t\)
- Quãng đường rơi theo phương thẳng đứng: \(y = \frac{1}{2} g \cdot t^2\)
3. Phương trình quỹ đạo:
Quỹ đạo của vật là đường cong parabol, có phương trình liên hệ giữa \(x\) và \(y\) như sau:
\[
y = \frac{g}{2v_0^2} x^2
\]
4. Thời gian rơi và tầm ném xa:
- Thời gian rơi: \(t_r = \sqrt{\frac{2h}{g}}\), trong đó \(h\) là độ cao ban đầu so với mặt đất.
- Tầm ném xa (quãng đường đi được theo phương ngang cho đến khi chạm đất): \(L = v_0 \cdot t_r\)
5. Ví dụ minh họa:
Giả sử một vật được ném ngang từ độ cao \(h = 20 \, \text{m}\) với vận tốc ban đầu \(v_0 = 10 \, \text{m/s}\). Hãy tính thời gian rơi và tầm ném xa của vật.
Ta có:
- Thời gian rơi: \(t_r = \sqrt{\frac{2 \cdot 20}{9.8}} \approx 2.02 \, \text{giây}\)
- Tầm ném xa: \(L = 10 \cdot 2.02 \approx 20.2 \, \text{m}\)
Vậy, vật sẽ rơi xuống mặt đất sau khoảng 2.02 giây và chạm đất ở khoảng cách 20.2 mét tính từ vị trí ném ban đầu.

Bài Tập Tiếng Anh: Chọn Đáp Án Đúng Trong Các Câu Điều Kiện
Dưới đây là một số bài tập về câu điều kiện để giúp bạn nắm vững kiến thức:
Bài tập 1: Câu Điều Kiện Loại 1
Chọn đáp án đúng cho mỗi câu sau:
- If it (rain), I (stay) at home.
- A. rains / will stay
- B. rained / would stay
- C. will rain / stay
- D. rains / stay
- If she (study) hard, she (pass) the exam.
- A. study / will pass
- B. studies / will pass
- C. studied / would pass
- D. studies / pass
Đáp án:
Đáp án:
Bài tập 2: Câu Điều Kiện Loại 2
Điền vào chỗ trống với động từ thích hợp:
- If I (be) you, I (not go) there.
- If they (have) enough time, they (travel) around the world.
Đáp án:
- If I were you, I wouldn't go there.
- If they had enough time, they would travel around the world.
Bài tập 3: Câu Điều Kiện Loại 3
Chọn đáp án đúng cho mỗi câu sau:
- If they (listen) to me, they (not have) problems.
- A. listen / would not have
- B. had listened / would not have had
- C. listened / would not have
- D. have listened / would not have had
- If you (leave) earlier, you (catch) the train.
- A. leave / would catch
- B. left / would have caught
- C. had left / would have caught
- D. had left / would catch
Đáp án:
Đáp án:
Ghi chú
Các câu điều kiện thường được sử dụng để diễn tả một tình huống có thể xảy ra, không có thật hoặc đã không xảy ra trong quá khứ. Hãy chú ý đến sự khác biệt giữa các loại câu điều kiện để chọn đáp án đúng.

Bài Tập Toán: Giải Bất Phương Trình Bậc Hai
Trong bài tập này, chúng ta sẽ cùng ôn lại và thực hành cách giải bất phương trình bậc hai. Bất phương trình bậc hai có dạng tổng quát như sau:
Hoặc:
Trong đó \(a\), \(b\), và \(c\) là các hệ số thực, với \(a \neq 0\). Để giải bất phương trình bậc hai, chúng ta thực hiện theo các bước sau:
- Tính biệt thức (Delta):
Đầu tiên, chúng ta tính giá trị của biệt thức Delta (Δ) theo công thức:
\[ \Delta = b^2 - 4ac \]Giá trị của Δ sẽ quyết định số nghiệm của phương trình bậc hai liên quan.
- Xác định nghiệm của phương trình bậc hai:
Dựa vào giá trị của Δ, chúng ta sẽ có:
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm phân biệt \(x_1\) và \(x_2\).
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép \(x_1 = x_2\).
- Nếu \(\Delta < 0\): Phương trình vô nghiệm thực (không có nghiệm trên tập số thực).
Công thức tính nghiệm trong trường hợp có nghiệm:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} \] - Vẽ bảng xét dấu:
Chúng ta lập bảng xét dấu của tam thức bậc hai trên từng khoảng nghiệm tìm được (nếu có). Điều này giúp xác định khoảng giá trị của \(x\) thỏa mãn bất phương trình.
- Kết luận tập nghiệm:
Dựa trên bảng xét dấu, kết luận tập nghiệm của bất phương trình. Kết quả có thể là các khoảng giá trị của \(x\) hoặc kết hợp các khoảng giá trị.
Ví dụ:
Giải bất phương trình sau:
Bước 1: Tính Delta:
Bước 2: Tìm nghiệm:
Bước 3: Lập bảng xét dấu:
| Khoảng | (-\(\infty\), 0.5) | (0.5, 1) | (1, \(\infty\)) |
| Dấu của \(2x^2 - 3x + 1\) | + | - | + |
Bước 4: Kết luận:
Bất phương trình \(2x^2 - 3x + 1 > 0\) có nghiệm là:
Hy vọng bài tập trên giúp bạn nắm vững phương pháp giải bất phương trình bậc hai. Hãy luyện tập thêm để cải thiện kỹ năng của mình!
Bài Tập Lý: Tính Lực Ma Sát
Trong bài tập này, chúng ta sẽ tính lực ma sát tác dụng lên một vật khi nó chuyển động trên bề mặt phẳng nằm ngang. Lực ma sát có thể được tính dựa trên định luật về ma sát, với công thức như sau:
\[
F_{ms} = \mu \cdot N
\]
Trong đó:
- \(F_{ms}\) là lực ma sát (đơn vị: Newton, N).
- \(\mu\) là hệ số ma sát giữa hai bề mặt (không có đơn vị).
- \(N\) là lực pháp tuyến tác dụng lên vật (đơn vị: Newton, N).
Bước 1: Xác định các lực tác dụng lên vật.
Khi vật nằm trên bề mặt phẳng nằm ngang, lực pháp tuyến \(N\) sẽ bằng trọng lực của vật, tức là:
\[
N = m \cdot g
\]
Trong đó:
- \(m\) là khối lượng của vật (đơn vị: kilogram, kg).
- \(g\) là gia tốc trọng trường, thường lấy giá trị \(g \approx 9.8 \, m/s^2\).
Bước 2: Tính lực ma sát.
Thay giá trị của \(N\) vào công thức lực ma sát, ta có:
\[
F_{ms} = \mu \cdot m \cdot g
\]
Ví dụ, nếu vật có khối lượng \(m = 10 \, kg\) và hệ số ma sát giữa vật và bề mặt là \(\mu = 0.3\), thì lực ma sát sẽ được tính như sau:
\[
F_{ms} = 0.3 \cdot 10 \, kg \cdot 9.8 \, m/s^2 = 29.4 \, N
\]
Do đó, lực ma sát tác dụng lên vật là \(29.4 \, N\).
Bước 3: Phân tích kết quả và áp dụng vào bài tập thực tế.
Với công thức và cách tính trên, bạn có thể áp dụng vào các bài tập khác nhau để tính toán lực ma sát, từ đó hiểu rõ hơn về các yếu tố ảnh hưởng đến lực này và cách nó ảnh hưởng đến chuyển động của vật.
Bài Tập Tiếng Anh: Sắp Xếp Từ Thành Câu Hoàn Chỉnh
Trong bài tập này, bạn sẽ được cung cấp một số từ hoặc cụm từ, và nhiệm vụ của bạn là sắp xếp chúng thành một câu hoàn chỉnh và có nghĩa trong tiếng Anh. Dưới đây là các bước hướng dẫn chi tiết:
- Đọc kỹ các từ hoặc cụm từ: Trước tiên, bạn cần đọc qua tất cả các từ hoặc cụm từ được cung cấp. Điều này giúp bạn xác định từ nào có thể là chủ ngữ, động từ, tân ngữ, trạng từ, hay các thành phần khác của câu.
- Xác định chủ ngữ và động từ chính: Tìm từ có chức năng làm chủ ngữ (subject) và động từ chính (main verb) trong câu. Thông thường, chủ ngữ là một danh từ hoặc đại từ, còn động từ chính là hành động hoặc trạng thái mà chủ ngữ thực hiện.
- Sắp xếp các thành phần phụ: Sau khi xác định được chủ ngữ và động từ, tiếp tục sắp xếp các thành phần phụ như tân ngữ (object), trạng từ (adverb), giới từ (preposition), tính từ (adjective), và các từ nối khác để tạo thành câu hoàn chỉnh.
- Kiểm tra lại trật tự từ: Sau khi sắp xếp, hãy đọc lại câu vừa hoàn thành để đảm bảo rằng nó có nghĩa và tuân theo ngữ pháp tiếng Anh.
Dưới đây là một ví dụ cụ thể:
Các từ được cung cấp: beautiful / a / she / flower / in / picked / the / garden
Thực hiện:
- Bước 1: Xác định chủ ngữ: she
- Bước 2: Xác định động từ: picked
- Bước 3: Xác định tân ngữ và trạng từ: a beautiful flower in the garden
Kết quả: She picked a beautiful flower in the garden.
Hãy thử làm một vài ví dụ khác để luyện tập và củng cố kỹ năng sắp xếp từ của bạn!
Bài Tập Toán: Tính Xác Suất
Xác suất là một trong những khái niệm cơ bản trong toán học và được áp dụng rộng rãi trong nhiều lĩnh vực. Để tính xác suất của một sự kiện xảy ra, ta cần làm theo các bước sau:
Xác định không gian mẫu: Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của một phép thử. Ký hiệu là \( S \).
Xác định sự kiện: Một sự kiện là một tập con của không gian mẫu. Giả sử sự kiện cần tính xác suất là \( A \).
Tính số phần tử của không gian mẫu: Ký hiệu số phần tử của không gian mẫu là \( n(S) \).
Tính số phần tử của sự kiện: Ký hiệu số phần tử của sự kiện là \( n(A) \).
Tính xác suất: Xác suất của sự kiện \( A \) xảy ra được tính bằng công thức:
\[
P(A) = \frac{n(A)}{n(S)}
\]
Ví dụ: Trong một hộp có 5 viên bi đỏ và 3 viên bi xanh, nếu rút ngẫu nhiên một viên bi thì xác suất để rút được viên bi đỏ là bao nhiêu?
Không gian mẫu: Tất cả các viên bi trong hộp, \( n(S) = 5 + 3 = 8 \) viên bi.
Sự kiện rút được viên bi đỏ, \( n(A) = 5 \).
Xác suất rút được viên bi đỏ:
\[
P(A) = \frac{5}{8} = 0.625
\]
Như vậy, xác suất để rút được một viên bi đỏ từ hộp là 0.625.