Chủ đề lịch thi đấu bóng đá ngoại hạng anh mu: Lịch thi đấu bóng đá Ngoại hạng Anh của Manchester United mùa giải 2024/2025 mang đến những trận đấu hấp dẫn, đầy kịch tính. Cùng cập nhật chi tiết từng trận đấu, thời gian và đối thủ của MU để không bỏ lỡ bất kỳ khoảnh khắc nào. Hãy theo dõi ngay để cổ vũ cho đội bóng yêu thích của bạn trong hành trình chinh phục ngôi vương!
Mục lục
- Lịch Thi Đấu Bóng Đá Ngoại Hạng Anh của Manchester United
- Lịch Thi Đấu Chi Tiết Của Manchester United Tại Ngoại Hạng Anh 2024/2025
- Các Trận Đấu Đáng Chú Ý Của Manchester United Tại Ngoại Hạng Anh 2024/2025
- Những Lưu Ý Trước Mùa Giải 2024/2025 Của Manchester United
- Phân Tích Và Dự Đoán Mùa Giải 2024/2025 Của Manchester United
- Dạng Bài Tập Toán (Ví Dụ Thêm Cho Chủ Đề Liên Quan)
- Dạng Bài Tập 1: Giải Phương Trình Bậc Hai
- Dạng Bài Tập 2: Tính Tích Phân Cơ Bản
- Dạng Bài Tập 3: Định Lý Hàm Số Liên Tục
- Dạng Bài Tập 4: Tìm Giá Trị Lớn Nhất Và Nhỏ Nhất Của Hàm Số
- Dạng Bài Tập 5: Ứng Dụng Đạo Hàm Để Khảo Sát Hàm Số
- Dạng Bài Tập 6: Giải Hệ Phương Trình Tuyến Tính
- Dạng Bài Tập 7: Bài Toán Thực Tế Sử Dụng Đạo Hàm
- Dạng Bài Tập 8: Tìm Chu Kỳ Của Hàm Số
- Dạng Bài Tập 9: Bài Toán Lãi Suất Trong Toán Tài Chính
- Dạng Bài Tập 10: Xác Suất Trong Biến Cố Độc Lập
Lịch Thi Đấu Bóng Đá Ngoại Hạng Anh của Manchester United
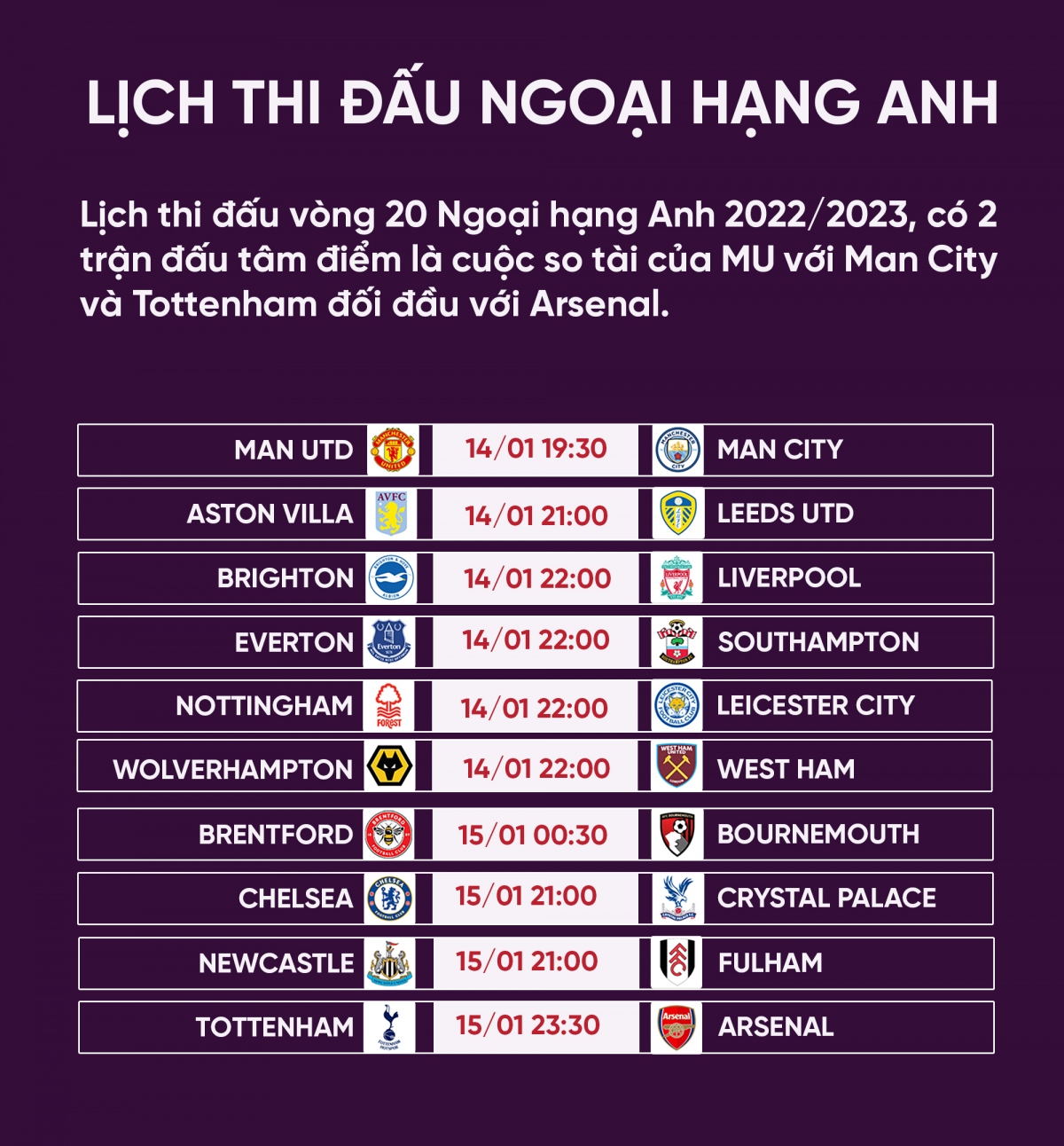
Lịch thi đấu của Manchester United (MU) trong mùa giải Ngoại Hạng Anh luôn được người hâm mộ bóng đá quan tâm đặc biệt. Dưới đây là tổng hợp lịch thi đấu chi tiết của MU trong thời gian tới.
1. Lịch Thi Đấu Chi Tiết
| Ngày | Thời gian | Đối thủ | Sân vận động |
|---|---|---|---|
| 02/09/2024 | 20:00 | Liverpool | Old Trafford |
| 09/09/2024 | 22:30 | Arsenal | Emirates |
| 16/09/2024 | 19:30 | Tottenham Hotspur | Old Trafford |
| 23/09/2024 | 21:00 | Chelsea | Stamford Bridge |
2. Các Trận Đấu Quan Trọng
- Manchester United vs Liverpool: Trận đấu kinh điển giữa hai đội bóng hàng đầu nước Anh, hứa hẹn mang đến nhiều cảm xúc cho người hâm mộ.
- Manchester United vs Arsenal: Cuộc đối đầu giữa hai đối thủ truyền kiếp sẽ mang lại những pha bóng kịch tính.
- Manchester United vs Chelsea: Trận đấu có thể ảnh hưởng lớn đến vị trí của MU trên bảng xếp hạng.
3. Cơ Hội Vô Địch
Manchester United đang có phong độ ổn định và được đánh giá là một trong những ứng cử viên hàng đầu cho chức vô địch Ngoại Hạng Anh mùa này. Với sự dẫn dắt của HLV tài ba và đội hình chất lượng, MU hoàn toàn có thể cạnh tranh sòng phẳng với các đối thủ khác.
Hãy cùng đón chờ những trận cầu đỉnh cao và cổ vũ cho Manchester United trong hành trình chinh phục ngôi vương mùa giải này!

.png)
Lịch Thi Đấu Chi Tiết Của Manchester United Tại Ngoại Hạng Anh 2024/2025
Dưới đây là lịch thi đấu chi tiết của Manchester United tại Ngoại hạng Anh mùa giải 2024/2025. Hãy cùng theo dõi để không bỏ lỡ bất kỳ trận đấu nào của Quỷ Đỏ.
| Vòng đấu | Ngày | Đối thủ | Địa điểm |
|---|---|---|---|
| Vòng 1 | 12/08/2024 | Brighton | Old Trafford |
| Vòng 2 | 19/08/2024 | Man City | Etihad Stadium |
| Vòng 3 | 26/08/2024 | Liverpool | Anfield |
| Vòng 4 | 02/09/2024 | Chelsea | Old Trafford |
| Vòng 5 | 16/09/2024 | Arsenal | Emirates Stadium |
| Vòng 6 | 23/09/2024 | Tottenham | Old Trafford |
| Vòng 7 | 30/09/2024 | Newcastle | St. James' Park |
Manchester United sẽ mở đầu mùa giải với trận đấu trên sân nhà Old Trafford trước Brighton. Tiếp đó, họ sẽ có trận derby thành Manchester đầy căng thẳng với Man City tại Etihad. Những trận đấu quan trọng khác bao gồm cuộc chạm trán với Liverpool tại Anfield và đối đầu với Chelsea trên sân nhà. Đừng bỏ lỡ những trận đấu này!
Các Trận Đấu Đáng Chú Ý Của Manchester United Tại Ngoại Hạng Anh 2024/2025
Mùa giải 2024/2025 hứa hẹn mang đến cho người hâm mộ những trận cầu đỉnh cao, nơi Manchester United sẽ phải đối đầu với nhiều đối thủ đáng gờm. Dưới đây là các trận đấu quan trọng nhất của MU trong mùa giải này.
- Derby Manchester: Trận đấu giữa Manchester United và Manchester City luôn là tâm điểm của sự chú ý. Vào vòng 2, MU sẽ đến làm khách tại sân Etihad, nơi họ sẽ cần thể hiện sức mạnh để giành điểm trước đối thủ cùng thành phố.
- Đối đầu Liverpool: Cuộc đối đầu giữa Manchester United và Liverpool tại Anfield vào vòng 3 luôn mang đến những cảm xúc mãnh liệt cho cả hai đội. Đây là trận đấu không chỉ vì 3 điểm mà còn vì danh dự.
- Chạm trán Arsenal: Vòng 5 sẽ chứng kiến Manchester United đối đầu với Arsenal tại sân Emirates. Đây là trận đấu quan trọng, ảnh hưởng trực tiếp đến cuộc đua top 4 của cả hai đội.
- Cuộc đọ sức với Chelsea: Tại vòng 4, Manchester United sẽ tiếp đón Chelsea trên sân nhà Old Trafford. Đây là một trong những trận đấu được mong đợi nhất mùa giải, khi hai đội bóng lớn tranh tài.
- Trận gặp Tottenham: MU sẽ đối đầu với Tottenham tại sân nhà Old Trafford vào vòng 6. Đây là trận đấu mà Quỷ Đỏ cần giành chiến thắng để duy trì vị thế trong cuộc đua vô địch.
Các trận đấu này không chỉ quan trọng về mặt điểm số mà còn ảnh hưởng lớn đến tâm lý và phong độ của đội bóng. Người hâm mộ hãy sẵn sàng để cổ vũ cho MU trong hành trình chinh phục Ngoại hạng Anh mùa này!

Những Lưu Ý Trước Mùa Giải 2024/2025 Của Manchester United
Mùa giải 2024/2025 đang đến gần, và Manchester United cần chuẩn bị kỹ lưỡng để đạt được thành công. Dưới đây là một số lưu ý quan trọng mà đội bóng và người hâm mộ cần ghi nhớ trước khi bước vào mùa giải mới.
- Những Gương Mặt Mới: Manchester United đã bổ sung thêm nhiều cầu thủ chất lượng trong kỳ chuyển nhượng. Việc làm quen và hòa nhập nhanh chóng của các tân binh sẽ quyết định sự thành công của đội bóng trong giai đoạn đầu mùa giải.
- Chiến Thuật Dự Kiến: HLV Erik ten Hag dự kiến sẽ tiếp tục sử dụng sơ đồ 4-2-3-1, nhấn mạnh vào việc kiểm soát bóng và chơi pressing cao. Tuy nhiên, sự linh hoạt trong chiến thuật là yếu tố cần thiết để đối phó với các đối thủ khác nhau.
- Lịch Thi Đấu Dày Đặc: Với việc tham gia nhiều giải đấu khác nhau, lịch thi đấu của MU sẽ rất dày đặc. Quản lý thể lực và xoay tua đội hình là chìa khóa để tránh chấn thương và đảm bảo phong độ ổn định trong suốt mùa giải.
- Tinh Thần Đồng Đội: Sự gắn kết trong đội hình sẽ là yếu tố quan trọng giúp MU vượt qua những thời điểm khó khăn. Tinh thần chiến đấu và sự đoàn kết sẽ là nền tảng vững chắc cho thành công của đội bóng.
Với sự chuẩn bị kỹ lưỡng và chiến thuật phù hợp, Manchester United hoàn toàn có thể kỳ vọng vào một mùa giải 2024/2025 đầy ấn tượng. Người hâm mộ hãy sẵn sàng để cổ vũ cho đội bóng trong hành trình chinh phục các danh hiệu!
Phân Tích Và Dự Đoán Mùa Giải 2024/2025 Của Manchester United
Mùa giải 2024/2025 hứa hẹn sẽ là một chặng đường đầy thử thách cho Manchester United. Dưới đây là những phân tích và dự đoán về khả năng thi đấu và thành tích của đội bóng trong mùa giải này.
- Cơ Hội Cạnh Tranh Chức Vô Địch: Với sự bổ sung lực lượng và chiến thuật ổn định, Manchester United được kỳ vọng sẽ là một trong những ứng cử viên nặng ký cho chức vô địch. Sự ổn định của các trụ cột và khả năng xoay tua đội hình sẽ quyết định thành bại của mùa giải.
- Những Đối Thủ Khó Chơi: Man City, Liverpool, và Arsenal là những đối thủ cạnh tranh trực tiếp với MU cho các vị trí dẫn đầu. Trận đấu với những đội này sẽ mang tính quyết định đến thứ hạng của Manchester United.
- Hiệu Suất Tấn Công: MU sở hữu nhiều cầu thủ tấn công tài năng như Rashford, Bruno Fernandes và tân binh mới gia nhập. Khả năng ghi bàn và sự linh hoạt trong lối chơi tấn công sẽ là điểm mạnh giúp đội bóng giành chiến thắng trong nhiều trận đấu quan trọng.
- Phong Độ Sân Nhà: Old Trafford luôn là pháo đài vững chắc, nơi mà Manchester United thường có những trận đấu thành công. Duy trì phong độ tốt tại sân nhà sẽ là yếu tố then chốt giúp đội bóng đạt được mục tiêu mùa giải.
- Dự Đoán Vị Trí Chung Cuộc: Với sự chuẩn bị kỹ lưỡng và tinh thần thi đấu quyết tâm, Manchester United có thể kết thúc mùa giải trong top 3, và nếu duy trì sự ổn định, cơ hội vô địch là hoàn toàn có thể.
Tóm lại, mùa giải 2024/2025 sẽ là một cuộc đua căng thẳng nhưng đầy hứa hẹn cho Manchester United. Với chiến lược đúng đắn và phong độ ổn định, Quỷ Đỏ có thể đạt được những thành công lớn trong mùa giải này.

Dạng Bài Tập Toán (Ví Dụ Thêm Cho Chủ Đề Liên Quan)
Dưới đây là một số dạng bài tập toán tiêu biểu kèm theo hướng dẫn giải chi tiết, giúp học sinh luyện tập và củng cố kiến thức liên quan.
- Bài Tập 1: Tính tổng các số tự nhiên từ 1 đến 100. Hướng dẫn: Sử dụng công thức tính tổng của cấp số cộng \(\sum_{i=1}^{n} i = \frac{n(n+1)}{2}\).
- Bài Tập 2: Giải phương trình bậc hai: \(ax^2 + bx + c = 0\). Hướng dẫn: Sử dụng công thức nghiệm \(\Delta = b^2 - 4ac\), nếu \(\Delta \geq 0\) thì tính nghiệm theo công thức \(x = \frac{-b \pm \sqrt{\Delta}}{2a}\).
- Bài Tập 3: Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(y = -2x^2 + 3x + 1\) trên đoạn \([0, 2]\). Hướng dẫn: Tính đạo hàm \(y'\) để tìm cực trị, sau đó so sánh giá trị của hàm số tại các điểm đầu đoạn và các điểm cực trị.
- Bài Tập 4: Tính diện tích hình tam giác biết ba cạnh \(a = 3\), \(b = 4\), \(c = 5\). Hướng dẫn: Sử dụng công thức Heron \(S = \sqrt{p(p-a)(p-b)(p-c)}\) với \(p = \frac{a+b+c}{2}\).
- Bài Tập 5: Tính thể tích khối cầu có bán kính \(r = 3\). Hướng dẫn: Sử dụng công thức tính thể tích khối cầu \(V = \frac{4}{3}\pi r^3\).
- Bài Tập 6: Tìm tập hợp nghiệm của bất phương trình \(2x - 3 > 0\). Hướng dẫn: Giải bất phương trình bằng cách chuyển vế và chia hai vế cho hệ số của \(x\).
- Bài Tập 7: Giải hệ phương trình \(\begin{cases} x + y = 5 \\ 2x - y = 1 \end{cases}\). Hướng dẫn: Sử dụng phương pháp thế hoặc phương pháp cộng đại số để tìm nghiệm.
- Bài Tập 8: Tính tích phân \(\int_0^1 (3x^2 + 2x + 1) \, dx\). Hướng dẫn: Sử dụng công thức tính tích phân cơ bản để giải.
- Bài Tập 9: Tính giới hạn \(\lim_{x \to 0} \frac{\sin x}{x}\). Hướng dẫn: Sử dụng kết quả giới hạn đặc biệt và định lý L'Hopital nếu cần.
- Bài Tập 10: Chứng minh rằng số \(2^{10} - 1\) là số chia hết cho 3. Hướng dẫn: Sử dụng tính chất của số mũ và phương pháp chia đa thức để chứng minh.
XEM THÊM:
Dạng Bài Tập 1: Giải Phương Trình Bậc Hai
Phương trình bậc hai là dạng toán cơ bản nhưng rất quan trọng trong chương trình học phổ thông. Dưới đây là hướng dẫn chi tiết cách giải phương trình bậc hai bằng cách sử dụng công thức nghiệm.
- Bước 1: Xác định các hệ số \(a\), \(b\), và \(c\) trong phương trình bậc hai có dạng tổng quát: \[ ax^2 + bx + c = 0 \] Ví dụ: Với phương trình \(2x^2 - 4x + 1 = 0\), ta có \(a = 2\), \(b = -4\), \(c = 1\).
- Bước 2: Tính biệt thức \(\Delta\) (Delta): \[ \Delta = b^2 - 4ac \] Ví dụ: Với \(a = 2\), \(b = -4\), \(c = 1\), ta có: \[ \Delta = (-4)^2 - 4 \times 2 \times 1 = 16 - 8 = 8 \]
- Bước 3: Dựa vào giá trị của \(\Delta\), xác định số nghiệm của phương trình:
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép.
- Nếu \(\Delta < 0\): Phương trình vô nghiệm thực.
- Bước 4: Tính nghiệm của phương trình bằng công thức: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \] Ví dụ: \[ x_1 = \frac{-(-4) + \sqrt{8}}{2 \times 2} = \frac{4 + 2\sqrt{2}}{4} = 1 + \frac{\sqrt{2}}{2} \] \[ x_2 = \frac{-(-4) - \sqrt{8}}{2 \times 2} = \frac{4 - 2\sqrt{2}}{4} = 1 - \frac{\sqrt{2}}{2} \]
- Bước 5: Kết luận và trình bày nghiệm của phương trình:
Phương trình \(2x^2 - 4x + 1 = 0\) có hai nghiệm phân biệt là:
\[ x_1 = 1 + \frac{\sqrt{2}}{2}, \quad x_2 = 1 - \frac{\sqrt{2}}{2} \]

Dạng Bài Tập 2: Tính Tích Phân Cơ Bản
Tính tích phân cơ bản là một dạng bài tập thường gặp trong chương trình toán học. Dưới đây là hướng dẫn chi tiết để giải bài toán tính tích phân của một hàm số trên một đoạn nhất định.
- Bước 1: Xác định hàm số cần tính tích phân và khoảng giới hạn tích phân. Ví dụ, với bài toán tính tích phân của hàm số \(f(x) = 3x^2 + 2x + 1\) trên đoạn \([0, 2]\), ta có: \[ \int_{0}^{2} (3x^2 + 2x + 1) \, dx \]
- Bước 2: Tính nguyên hàm của hàm số \(f(x)\). Để tính nguyên hàm, áp dụng các công thức cơ bản: \[ \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \] Với ví dụ trên, nguyên hàm của \(f(x)\) là: \[ \int (3x^2) \, dx = x^3, \quad \int (2x) \, dx = x^2, \quad \int 1 \, dx = x \] Vậy nguyên hàm của \(f(x)\) là: \[ F(x) = x^3 + x^2 + x \]
- Bước 3: Tính giá trị của nguyên hàm tại các điểm giới hạn trên và dưới:
- Giá trị tại \(x = 2\): \[ F(2) = 2^3 + 2^2 + 2 = 8 + 4 + 2 = 14 \]
- Giá trị tại \(x = 0\): \[ F(0) = 0^3 + 0^2 + 0 = 0 \]
- Bước 4: Tính giá trị tích phân bằng cách lấy hiệu giá trị của nguyên hàm tại giới hạn trên và giới hạn dưới: \[ \int_{0}^{2} (3x^2 + 2x + 1) \, dx = F(2) - F(0) = 14 - 0 = 14 \]
- Bước 5: Kết luận, tích phân của hàm số \(f(x) = 3x^2 + 2x + 1\) trên đoạn \([0, 2]\) bằng 14.

Dạng Bài Tập 3: Định Lý Hàm Số Liên Tục
Định lý hàm số liên tục là một trong những định lý cơ bản trong giải tích. Để hiểu rõ định lý này, chúng ta cần nắm vững một số khái niệm liên quan như giới hạn của hàm số và tính liên tục tại một điểm. Dưới đây là các bước cụ thể để giải quyết bài tập về định lý hàm số liên tục.
-
Nhắc lại định nghĩa hàm số liên tục:
Một hàm số \( f(x) \) được gọi là liên tục tại điểm \( x_0 \) nếu thỏa mãn ba điều kiện sau:
- \( f(x_0) \) được xác định.
- \( \lim_{x \to x_0} f(x) \) tồn tại.
- \( \lim_{x \to x_0} f(x) = f(x_0) \).
-
Xét tính liên tục của hàm số tại một điểm:
Giả sử cho hàm số \( f(x) = \frac{x^2 - 4}{x - 2} \) và cần kiểm tra xem hàm số có liên tục tại \( x = 2 \) hay không.
Bước 1: Xét hàm số tại \( x = 2 \): \( f(2) = \frac{2^2 - 4}{2 - 2} = \frac{0}{0} \), do đó không xác định trực tiếp.
Bước 2: Tìm giới hạn của hàm số khi \( x \) tiến đến 2:
\[ \lim_{x \to 2} \frac{x^2 - 4}{x - 2} = \lim_{x \to 2} \frac{(x-2)(x+2)}{x-2} = \lim_{x \to 2} (x + 2) = 4 \]Bước 3: Kết luận: Vì \( f(x) \) không xác định tại \( x = 2 \) nhưng giới hạn tồn tại, do đó hàm số không liên tục tại điểm này.
-
Sử dụng định lý giá trị trung bình để chứng minh tính liên tục:
Định lý giá trị trung bình phát biểu rằng nếu một hàm số liên tục trên đoạn \([a, b]\) thì tồn tại ít nhất một điểm \( c \) trong đoạn \((a, b)\) sao cho:
\[ f'(c) = \frac{f(b) - f(a)}{b - a} \]Ví dụ, xét hàm số \( f(x) = x^3 - 3x + 1 \) trên đoạn \([-1, 2]\). Ta cần chứng minh rằng hàm số này có ít nhất một điểm \( c \) trong đoạn này mà tại đó đạo hàm bằng giá trị trung bình của hàm số trên đoạn.
Bước 1: Tính giá trị hàm số tại hai đầu đoạn:
- \( f(-1) = (-1)^3 - 3(-1) + 1 = 3 \)
- \( f(2) = 2^3 - 3(2) + 1 = 3 \)
Bước 2: Tính giá trị trung bình:
\[ \frac{f(2) - f(-1)}{2 - (-1)} = \frac{3 - 3}{3} = 0 \]Bước 3: Đạo hàm của hàm số \( f'(x) = 3x^2 - 3 \). Ta cần tìm \( c \) sao cho \( 3c^2 - 3 = 0 \). Điều này dẫn đến \( c = 1 \).
Vậy hàm số thỏa mãn định lý giá trị trung bình và liên tục trên đoạn đã cho.
Dạng Bài Tập 4: Tìm Giá Trị Lớn Nhất Và Nhỏ Nhất Của Hàm Số
Trong giải tích, việc tìm giá trị lớn nhất và nhỏ nhất của một hàm số là một kỹ năng quan trọng. Đây là quá trình xác định các giá trị mà hàm số đạt được tại các điểm đặc biệt, như điểm cực đại, cực tiểu, hoặc tại các biên của miền xác định.
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f(x)\), chúng ta cần thực hiện các bước sau:
- Tính đạo hàm của hàm số:
Tính đạo hàm bậc nhất của hàm số \(f(x)\), tức là tìm \(f'(x)\).
\[ f'(x) = \frac{d}{dx} f(x) \] - Tìm các điểm tới hạn:
Giải phương trình \(f'(x) = 0\) để tìm các giá trị \(x\) tại đó đạo hàm bằng 0, hoặc tìm các điểm mà tại đó đạo hàm không xác định.
\[ f'(x) = 0 \quad \text{hoặc} \quad f'(x) \text{ không xác định} \] - Xác định giá trị lớn nhất và nhỏ nhất:
Đánh giá hàm số tại các điểm tới hạn vừa tìm được, và tại các biên (nếu có) của miền xác định.
So sánh các giá trị của hàm số tại các điểm này để xác định giá trị lớn nhất và nhỏ nhất.
Ví dụ, xét hàm số đơn giản:
- Bước 1: Tính đạo hàm của hàm số: \[ f'(x) = 3x^2 - 6x \]
- Bước 2: Tìm các điểm tới hạn bằng cách giải phương trình \(f'(x) = 0\):
\[
3x^2 - 6x = 0 \quad \Rightarrow \quad x(x - 2) = 0
\]
Vậy, ta có hai điểm tới hạn là \(x = 0\) và \(x = 2\).
- Bước 3: Đánh giá hàm số tại các điểm này:
- Với \(x = 0\): \[ f(0) = 0^3 - 3(0)^2 + 4 = 4 \]
- Với \(x = 2\): \[ f(2) = 2^3 - 3(2)^2 + 4 = 8 - 12 + 4 = 0
So sánh các giá trị này, ta thấy giá trị lớn nhất của hàm số là 4 tại \(x = 0\) và giá trị nhỏ nhất là 0 tại \(x = 2\).
Phương pháp này có thể áp dụng cho bất kỳ hàm số nào miễn là chúng ta có thể tính được đạo hàm của nó và tìm được các điểm tới hạn. Đây là một kỹ năng cơ bản nhưng quan trọng trong việc phân tích và tối ưu hóa hàm số.

Dạng Bài Tập 5: Ứng Dụng Đạo Hàm Để Khảo Sát Hàm Số
Trong toán học, đạo hàm là công cụ mạnh mẽ giúp chúng ta phân tích sự biến thiên của hàm số. Việc sử dụng đạo hàm để khảo sát hàm số là một phần quan trọng trong các bài toán liên quan đến cực trị, tiệm cận, và đồ thị hàm số.
Để khảo sát hàm số bằng đạo hàm, chúng ta cần thực hiện các bước sau:
- Xác định tập xác định của hàm số: Trước tiên, ta cần xác định tập xác định \(D\) của hàm số \(f(x)\). Đây là tập hợp tất cả các giá trị của \(x\) mà tại đó hàm số được định nghĩa.
- Tính đạo hàm \(f'(x)\) của hàm số: Đạo hàm \(f'(x)\) cho biết tốc độ thay đổi của hàm số tại mỗi điểm. Công thức tính đạo hàm phụ thuộc vào dạng của hàm số ban đầu.
- Tìm các điểm tới hạn: Các điểm tới hạn là những giá trị của \(x\) tại đó \(f'(x) = 0\) hoặc \(f'(x)\) không xác định. Đây là các điểm mà tại đó hàm số có thể đạt cực đại, cực tiểu hoặc điểm uốn.
- Khảo sát dấu của đạo hàm \(f'(x)\): Dấu của \(f'(x)\) giúp ta xác định khoảng tăng, giảm của hàm số. Cụ thể:
- Nếu \(f'(x) > 0\) trên một khoảng, thì hàm số đồng biến (tăng) trên khoảng đó.
- Nếu \(f'(x) < 0\) trên một khoảng, thì hàm số nghịch biến (giảm) trên khoảng đó.
- Xác định cực trị: Dựa vào việc khảo sát dấu của \(f'(x)\), ta có thể xác định các điểm cực đại và cực tiểu của hàm số. Nếu hàm số chuyển từ đồng biến sang nghịch biến tại một điểm, thì đó là điểm cực đại. Ngược lại, nếu hàm số chuyển từ nghịch biến sang đồng biến, thì đó là điểm cực tiểu.
- Khảo sát đạo hàm bậc hai (nếu cần): Đạo hàm bậc hai \(f''(x)\) giúp ta xác định tính lồi, lõm của đồ thị hàm số và kiểm tra tính chất cực trị của các điểm tới hạn. Cụ thể:
- Nếu \(f''(x) > 0\), đồ thị hàm số lồi và điểm tới hạn là cực tiểu.
- Nếu \(f''(x) < 0\), đồ thị hàm số lõm và điểm tới hạn là cực đại.
- Lập bảng biến thiên và vẽ đồ thị hàm số: Từ các thông tin đã thu thập được, ta lập bảng biến thiên, xác định các đặc điểm của đồ thị như khoảng đồng biến, nghịch biến, cực trị, điểm uốn và cuối cùng là vẽ đồ thị của hàm số.
Ví dụ, xét hàm số \(f(x) = x^3 - 3x^2 + 2x + 1\). Chúng ta sẽ thực hiện các bước trên để khảo sát và vẽ đồ thị của hàm số này.
Dạng Bài Tập 6: Giải Hệ Phương Trình Tuyến Tính
Giải hệ phương trình tuyến tính là một trong những dạng bài toán cơ bản và quan trọng trong đại số tuyến tính. Một hệ phương trình tuyến tính bao gồm nhiều phương trình tuyến tính với các biến số chung, và nhiệm vụ của chúng ta là tìm ra các giá trị của các biến sao cho tất cả các phương trình trong hệ đều được thỏa mãn.
Để giải hệ phương trình tuyến tính, chúng ta có thể áp dụng các phương pháp sau:
- Phương pháp thế: Đây là phương pháp đơn giản nhất để giải hệ hai phương trình hai ẩn. Ta sẽ biến đổi một phương trình thành dạng biểu thức của một ẩn theo ẩn còn lại, rồi thế vào phương trình thứ hai để tìm giá trị của các ẩn.
- Phương pháp cộng đại số: Trong phương pháp này, ta cộng hoặc trừ hai phương trình của hệ để loại bỏ một ẩn, từ đó rút gọn hệ và tìm được giá trị của các biến. Phương pháp này đặc biệt hiệu quả khi hệ có nhiều phương trình và biến.
- Phương pháp ma trận: Đối với hệ phương trình nhiều biến, phương pháp ma trận là công cụ mạnh mẽ. Ta biểu diễn hệ phương trình dưới dạng ma trận và sử dụng các phép biến đổi ma trận để đưa ma trận về dạng tam giác hoặc dạng bậc thang, từ đó dễ dàng tìm ra nghiệm của hệ.
- Phương pháp Cramer: Nếu hệ phương trình có số phương trình bằng số ẩn và định thức của ma trận hệ số khác không, ta có thể sử dụng định lý Cramer để tìm nghiệm. Mỗi nghiệm được xác định thông qua tỉ số của các định thức con.
Dưới đây là một ví dụ minh họa:
Xét hệ phương trình tuyến tính:
Sử dụng phương pháp thế:
- Biến đổi phương trình thứ nhất để tìm \( y \) theo \( x \): \[ y = \frac{5 - 2x}{3} \]
- Thế giá trị của \( y \) vào phương trình thứ hai: \[ 4x - \frac{5 - 2x}{3} = 6 \] Nhân cả hai vế với 3 để loại mẫu: \[ 12x - (5 - 2x) = 18 \] Rút gọn phương trình: \[ 14x = 23 \quad \Rightarrow \quad x = \frac{23}{14} \]
- Thế giá trị của \( x \) vào biểu thức tìm được ở bước 1: \[ y = \frac{5 - 2 \times \frac{23}{14}}{3} = \frac{1}{42} \]
Vậy nghiệm của hệ là \( x = \frac{23}{14} \) và \( y = \frac{1}{42} \).
Dạng Bài Tập 7: Bài Toán Thực Tế Sử Dụng Đạo Hàm
Trong dạng bài tập này, chúng ta sẽ ứng dụng đạo hàm để giải quyết các bài toán thực tế. Đây là một phần quan trọng trong giải tích, giúp chúng ta không chỉ hiểu rõ lý thuyết mà còn áp dụng vào các vấn đề trong đời sống.
1. Xác định các bài toán thực tế
Trước hết, ta cần nhận diện các bài toán thực tế có thể giải quyết bằng cách sử dụng đạo hàm. Các bài toán này thường liên quan đến:
- Tối ưu hóa: Tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số, chẳng hạn như tối đa hóa lợi nhuận hoặc tối thiểu hóa chi phí.
- Chuyển động: Xác định vận tốc tức thời hoặc gia tốc tại một thời điểm nào đó.
- Chi phí và lợi nhuận: Phân tích mối quan hệ giữa chi phí sản xuất và lợi nhuận để đưa ra quyết định kinh doanh hợp lý.
2. Ví dụ minh họa
Xét bài toán sau: Một công ty muốn sản xuất một sản phẩm sao cho chi phí sản xuất là thấp nhất. Giả sử hàm chi phí \(C(x)\) là một hàm số bậc hai theo sản lượng \(x\), có dạng:
Nhiệm vụ của chúng ta là tìm giá trị \(x\) sao cho chi phí \(C(x)\) là nhỏ nhất.
3. Giải quyết bài toán
- Bước 1: Tính đạo hàm của hàm chi phí \(C(x)\): \[ C'(x) = 2ax + b \]
- Bước 2: Tìm giá trị \(x\) sao cho đạo hàm \(C'(x) = 0\): \[ 2ax + b = 0 \Rightarrow x = -\frac{b}{2a} \]
- Bước 3: Xác định giá trị nhỏ nhất của chi phí bằng cách thay \(x\) vừa tìm được vào hàm chi phí \(C(x)\).
4. Kết luận
Qua bài toán trên, chúng ta thấy rằng việc sử dụng đạo hàm để giải quyết các bài toán thực tế không chỉ giúp tối ưu hóa các quá trình sản xuất và kinh doanh mà còn giúp hiểu rõ hơn về mối quan hệ giữa các biến số trong một bài toán. Đây là một ứng dụng rất mạnh mẽ và thiết thực của toán học trong cuộc sống hàng ngày.
Dạng Bài Tập 8: Tìm Chu Kỳ Của Hàm Số
Chu kỳ của một hàm số là một trong những tính chất quan trọng, đặc biệt khi khảo sát các hàm lượng giác hoặc các hàm số có tính chất tuần hoàn. Việc xác định chu kỳ giúp ta hiểu rõ hơn về hành vi của hàm số khi nó lặp lại theo thời gian.
Dưới đây là quy trình cơ bản để tìm chu kỳ của một hàm số:
-
Bước 1: Xác định dạng của hàm số
Hàm số cần tìm chu kỳ có thể là các hàm lượng giác như \( \sin(x) \), \( \cos(x) \), hoặc các hàm số tuần hoàn khác. Trước hết, ta cần xác định dạng chính xác của hàm số.
-
Bước 2: Tìm chu kỳ cơ bản
Nếu hàm số là hàm lượng giác cơ bản, như \( \sin(x) \) hoặc \( \cos(x) \), thì chu kỳ cơ bản của chúng là \( 2\pi \). Nếu hàm số là \( \tan(x) \) hoặc \( \cot(x) \), chu kỳ cơ bản sẽ là \( \pi \).
-
Bước 3: Xác định chu kỳ tổng quát
Nếu hàm số có dạng \( y = a \cdot f(bx + c) + d \), thì chu kỳ của hàm số sẽ là:
\[ T = \frac{T_0}{|b|} \]
Trong đó, \( T_0 \) là chu kỳ cơ bản của hàm \( f(x) \), và \( b \) là hệ số của biến \( x \) trong hàm số đã cho.
-
Bước 4: Kiểm tra và xác nhận
Sau khi tính toán được chu kỳ, ta cần kiểm tra lại bằng cách thay các giá trị vào hàm số và xác nhận rằng hàm số lặp lại sau mỗi chu kỳ đã tìm.
Ví dụ, xét hàm số \( y = 3\sin(2x) + 5 \). Ta có:
- Chu kỳ cơ bản của \( \sin(x) \) là \( 2\pi \).
- Hệ số \( b = 2 \) nên chu kỳ của hàm số là \( \frac{2\pi}{2} = \pi \).
Vậy, chu kỳ của hàm số \( y = 3\sin(2x) + 5 \) là \( \pi \).
Dạng Bài Tập 9: Bài Toán Lãi Suất Trong Toán Tài Chính
Bài toán lãi suất là một trong những ứng dụng quan trọng của toán tài chính. Để giải quyết những bài toán này, ta cần hiểu rõ các khái niệm về lãi đơn, lãi kép, và cách tính giá trị tương lai của các khoản đầu tư.
Dưới đây là các bước cơ bản để giải quyết một bài toán về lãi suất:
-
Xác định loại lãi suất: Đầu tiên, xác định xem bài toán yêu cầu tính lãi đơn hay lãi kép. Lãi đơn chỉ tính lãi trên số vốn ban đầu, trong khi lãi kép tính lãi trên cả vốn và lãi phát sinh.
-
Công thức tính lãi suất: Sử dụng các công thức sau tùy thuộc vào loại lãi suất:
- Lãi đơn: \[ A = P(1 + rt) \] trong đó \( P \) là số tiền gốc, \( r \) là lãi suất, và \( t \) là thời gian.
- Lãi kép: \[ A = P(1 + \frac{r}{n})^{nt} \] trong đó \( n \) là số lần gộp lãi trong một năm.
Tính giá trị tương lai: Áp dụng công thức tương ứng để tìm giá trị tương lai của khoản đầu tư sau một thời gian \( t \).
-
So sánh kết quả: Cuối cùng, nếu bài toán yêu cầu, so sánh giá trị tương lai với các phương án khác nhau để đưa ra quyết định tối ưu.
Ví dụ: Giả sử bạn đầu tư 10 triệu đồng với lãi suất 5%/năm, tính lãi kép hàng quý trong 3 năm. Áp dụng công thức trên, ta có:
\[ A = 10,000,000 \times \left(1 + \frac{0.05}{4}\right)^{4 \times 3} = 10,000,000 \times \left(1.0125\right)^{12} \approx 11,616,068 \, \text{đồng} \]
Như vậy, sau 3 năm, bạn sẽ có khoảng 11,616,068 đồng.
Dạng Bài Tập 10: Xác Suất Trong Biến Cố Độc Lập
Xác suất trong các biến cố độc lập là một khái niệm quan trọng trong xác suất thống kê. Biến cố độc lập là những biến cố mà xác suất xảy ra của một biến cố không bị ảnh hưởng bởi sự xảy ra hay không xảy ra của các biến cố khác.
Dưới đây là cách tiếp cận để giải quyết các bài toán xác suất trong biến cố độc lập:
-
Xác định các biến cố: Đầu tiên, xác định rõ ràng các biến cố tham gia trong bài toán. Kiểm tra xem chúng có độc lập với nhau hay không.
-
Sử dụng công thức xác suất cho biến cố độc lập: Nếu các biến cố là độc lập, xác suất của biến cố tổng hợp sẽ bằng tích các xác suất của từng biến cố. Công thức là:
\[
P(A \cap B) = P(A) \times P(B)
\] -
Tính xác suất: Thay các giá trị xác suất đã biết vào công thức và tính toán kết quả. Ví dụ, nếu \( P(A) = 0.5 \) và \( P(B) = 0.4 \), thì:
\[
P(A \cap B) = 0.5 \times 0.4 = 0.2
\] -
Kiểm tra kết quả: Đảm bảo rằng kết quả nằm trong khoảng từ 0 đến 1, vì xác suất không bao giờ vượt quá các giá trị này.
Ví dụ thực tế: Giả sử bạn tung hai con xúc xắc, mỗi con có xác suất xuất hiện mặt 6 là \( \frac{1}{6} \). Vì các lần tung xúc xắc là độc lập, xác suất để cả hai con xúc xắc đều xuất hiện mặt 6 là:
\[
P(\text{Xúc xắc 1 ra 6} \cap \text{Xúc xắc 2 ra 6}) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36}
\]
Vì vậy, xác suất để cả hai con xúc xắc đều ra mặt 6 là \( \frac{1}{36} \).