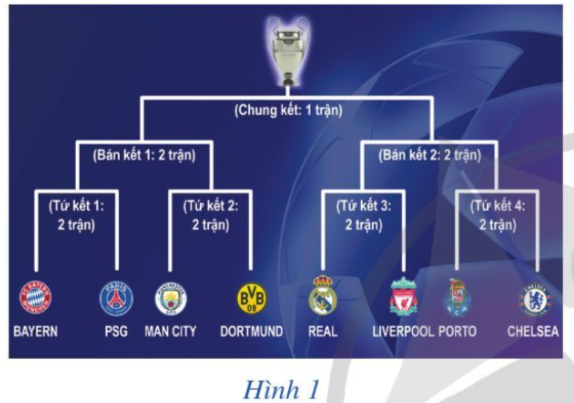
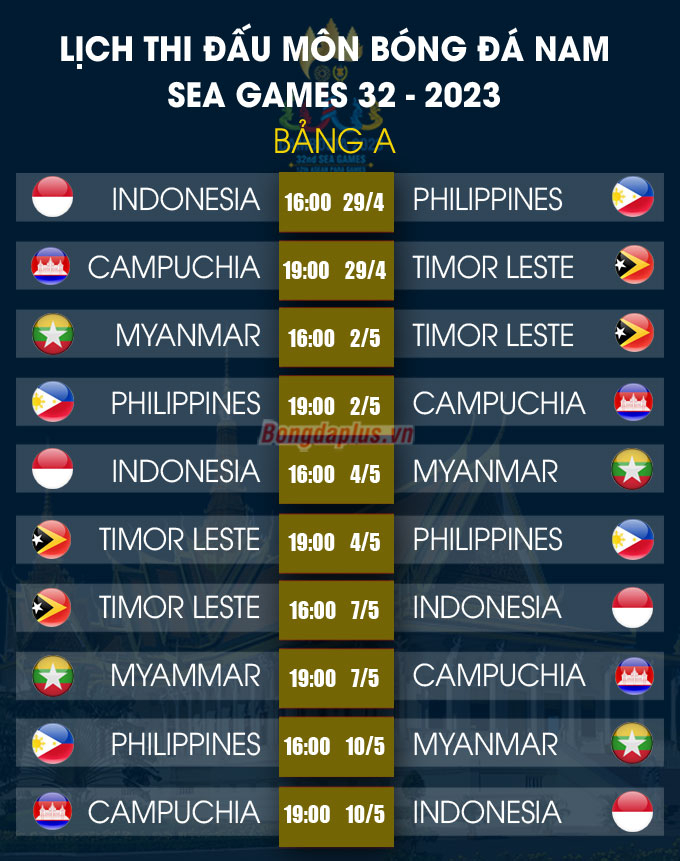
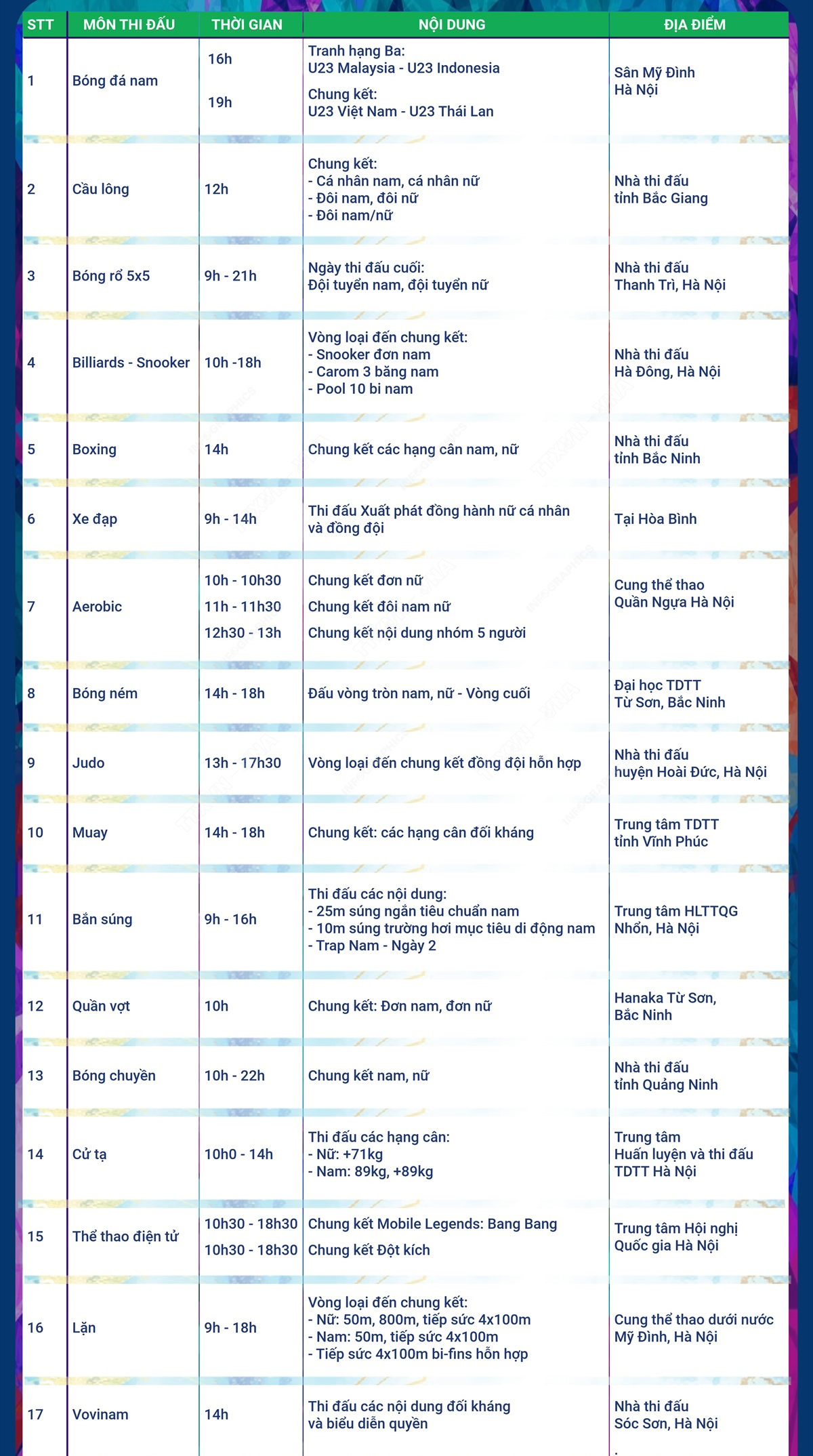
Chủ đề lịch thi đấu bóng đá tháng 8: Lịch thi đấu bóng đá tháng 8 hứa hẹn mang đến những trận cầu sôi động và kịch tính từ các giải đấu hàng đầu thế giới. Cập nhật chi tiết lịch thi đấu, thông tin về các đội bóng và nhận định chuyên gia giúp bạn không bỏ lỡ bất kỳ trận đấu nào trong tháng 8 này.
Mục lục
- Lịch Thi Đấu Bóng Đá Tháng 8
- 4. Lịch Thi Đấu Giải Bundesliga
- 5. Lịch Thi Đấu Giải Ligue 1
- 6. Lịch Thi Đấu Cúp C1 Châu Âu
- 7. Lịch Thi Đấu Các Giải Quốc Gia Khác
- 8. Lịch Thi Đấu Đội Tuyển Việt Nam
- 9. Lịch Thi Đấu Bóng Đá Nữ
- 10. Lịch Thi Đấu Các Giải Trẻ
- 11. Bài Tập Toán: Giải Hệ Phương Trình
- 12. Bài Tập Lý: Động Lực Học Chất Điểm
- 13. Bài Tập Toán: Tích Phân Bất Định
- 14. Bài Tập Lý: Điện Tích và Điện Trường
- 15. Bài Tập Tiếng Anh: Chia Thì Động Từ
- 16. Bài Tập Toán: Giải Bất Đẳng Thức
- 17. Bài Tập Lý: Nhiệt Học
- 18. Bài Tập Tiếng Anh: Câu Điều Kiện
- 19. Bài Tập Toán: Đạo Hàm và Ứng Dụng
- 20. Bài Tập Lý: Từ Trường và Ứng Dụng
Lịch Thi Đấu Bóng Đá Tháng 8
Tháng 8 là thời điểm khởi động của nhiều giải đấu bóng đá quan trọng trên thế giới như Ngoại hạng Anh, La Liga, Serie A, và nhiều giải đấu khác. Dưới đây là tổng hợp chi tiết lịch thi đấu bóng đá trong tháng 8.
1. Lịch Thi Đấu Giải Ngoại Hạng Anh
- Vòng 1:
- Ngày 12/08: Manchester City vs Burnley
- Ngày 13/08: Chelsea vs Liverpool
- Ngày 13/08: Manchester United vs Wolverhampton
- Vòng 2:
- Ngày 19/08: Arsenal vs Fulham
- Ngày 20/08: Tottenham vs Brentford
- Ngày 21/08: Newcastle vs Aston Villa
2. Lịch Thi Đấu Giải La Liga
- Ngày 12/08: Barcelona vs Real Sociedad
- Ngày 13/08: Real Madrid vs Athletic Bilbao
- Ngày 14/08: Valencia vs Sevilla
- Ngày 19/08: Atlético Madrid vs Rayo Vallecano
- Ngày 20/08: Villarreal vs Getafe
- Ngày 21/08: Betis vs Celta Vigo
3. Lịch Thi Đấu Giải Serie A
- Ngày 12/08: Inter Milan vs Napoli
- Ngày 13/08: Juventus vs Lazio
- Ngày 14/08: AC Milan vs Roma
- Ngày 19/08: Fiorentina vs Sassuolo
- Ngày 20/08: Torino vs Bologna
- Ngày 21/08: Sampdoria vs Genoa
4. Các Giải Đấu Khác
- Ligue 1:
- Ngày 12/08: PSG vs Marseille
- Ngày 13/08: Lyon vs Monaco
- Ngày 14/08: Lille vs Rennes
- Bundesliga:
- Ngày 12/08: Bayern Munich vs Borussia Dortmund
- Ngày 13/08: RB Leipzig vs Bayer Leverkusen
- Ngày 14/08: Schalke 04 vs Eintracht Frankfurt
5. Đặc Điểm Nổi Bật
Tháng 8 chứng kiến sự khởi động đầy sôi động của các giải đấu lớn. Đây là giai đoạn quan trọng để các câu lạc bộ thể hiện sức mạnh, chuẩn bị cho một mùa giải mới đầy cạnh tranh. Ngoài các giải đấu lớn, nhiều trận đấu trong khuôn khổ các giải quốc nội và quốc tế cũng diễn ra, mang lại nhiều cơ hội thưởng thức bóng đá đỉnh cao cho người hâm mộ.
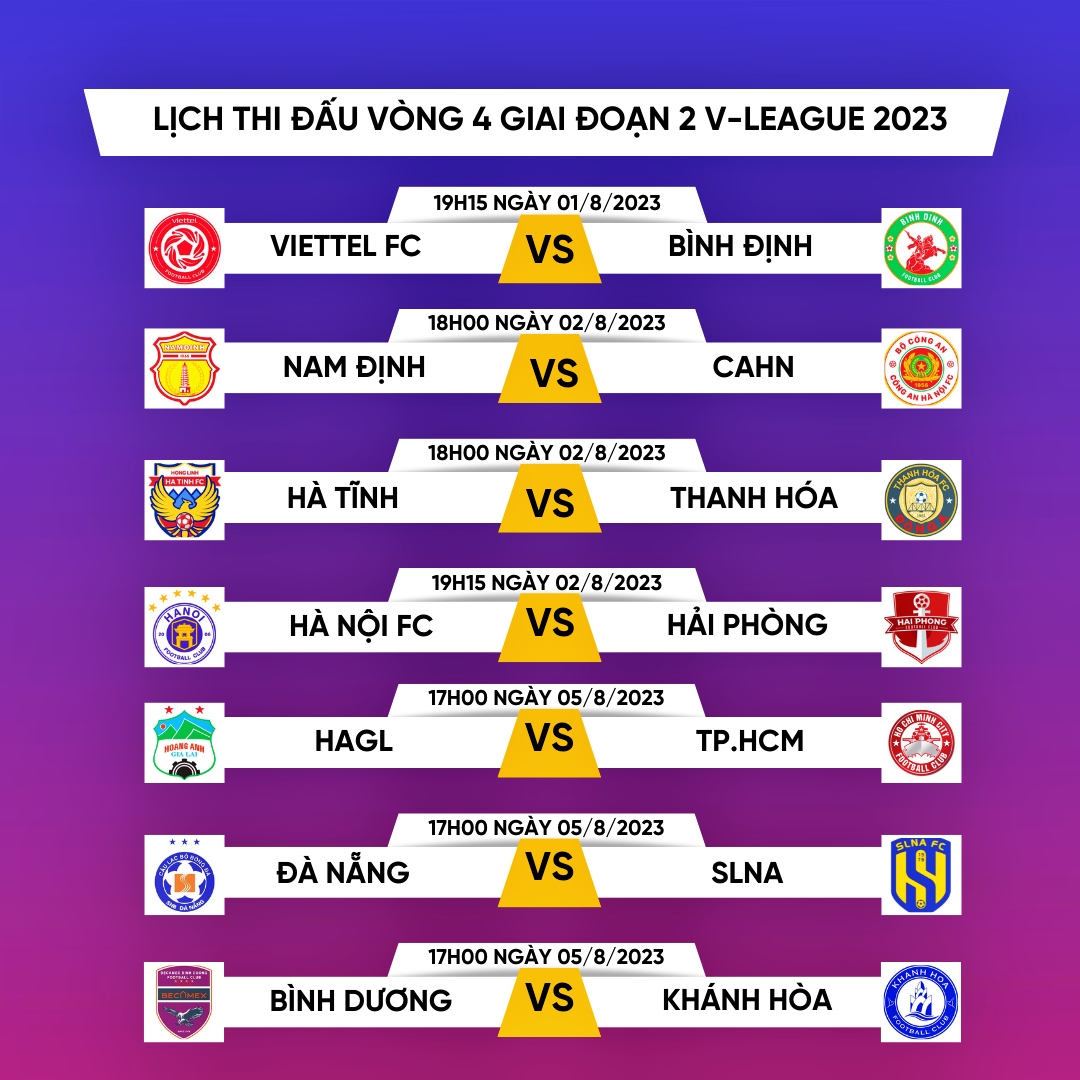
.png)
4. Lịch Thi Đấu Giải Bundesliga
Tháng 8 này, Bundesliga bắt đầu với những trận đấu sôi động, nơi các đội bóng như Bayern Munich, Borussia Dortmund và RB Leipzig sẽ cạnh tranh gay gắt. Dưới đây là lịch thi đấu chi tiết của các vòng đấu trong tháng 8:
- Vòng 1:
- Ngày 18/08: Bayern Munich vs Werder Bremen
- Ngày 19/08: Borussia Dortmund vs Mainz
- Ngày 20/08: RB Leipzig vs Stuttgart
- Ngày 21/08: Union Berlin vs Bayer Leverkusen
- Vòng 2:
- Ngày 25/08: Borussia Mönchengladbach vs Bayern Munich
- Ngày 26/08: VfL Wolfsburg vs Borussia Dortmund
- Ngày 27/08: Eintracht Frankfurt vs RB Leipzig
- Ngày 28/08: SC Freiburg vs Hoffenheim
- Vòng 3:
- Ngày 01/09: Bayern Munich vs Augsburg
- Ngày 02/09: Borussia Dortmund vs SC Freiburg
- Ngày 03/09: Bayer Leverkusen vs Eintracht Frankfurt
- Ngày 04/09: RB Leipzig vs Union Berlin
Bundesliga tháng 8 hứa hẹn sẽ mang đến những trận đấu đầy cảm xúc với những màn trình diễn đỉnh cao từ các câu lạc bộ lớn. Bayern Munich và Borussia Dortmund sẽ tiếp tục cuộc đua vô địch, trong khi các đội bóng khác như RB Leipzig và Union Berlin cũng sẽ nỗ lực để tạo bất ngờ.
5. Lịch Thi Đấu Giải Ligue 1
Giải đấu Ligue 1 tháng 8 khởi động với sự tham gia của những đội bóng mạnh nhất nước Pháp như Paris Saint-Germain (PSG), Olympique Lyon, và Marseille. Dưới đây là lịch thi đấu chi tiết của các vòng đấu trong tháng 8:
- Vòng 1:
- Ngày 12/08: Paris Saint-Germain vs Lorient
- Ngày 13/08: Marseille vs Reims
- Ngày 14/08: Lyon vs Brest
- Ngày 15/08: Lille vs Nantes
- Vòng 2:
- Ngày 19/08: Monaco vs Strasbourg
- Ngày 20/08: Rennes vs Le Havre
- Ngày 21/08: Montpellier vs Toulouse
- Ngày 22/08: Nice vs Marseille
- Vòng 3:
- Ngày 26/08: Paris Saint-Germain vs Lens
- Ngày 27/08: Lyon vs Saint-Étienne
- Ngày 28/08: Marseille vs Metz
- Ngày 29/08: Lille vs Angers
Ligue 1 tháng 8 hứa hẹn sẽ mang lại nhiều bất ngờ với sự cạnh tranh khốc liệt giữa các đội bóng hàng đầu. PSG, với đội hình mạnh mẽ, sẽ tiếp tục hành trình bảo vệ ngôi vương, trong khi các đội như Lyon và Marseille sẽ nỗ lực hết mình để gây khó khăn cho họ.

6. Lịch Thi Đấu Cúp C1 Châu Âu
Tháng 8 năm 2024, Cúp C1 Châu Âu (UEFA Champions League) bước vào giai đoạn vòng sơ loại đầy căng thẳng và quyết liệt, nhằm xác định những đội bóng cuối cùng tham dự vòng bảng. Đây là thời điểm mà các đội bóng từ các giải đấu lớn nhỏ khắp châu Âu thi đấu với nhau để giành quyền bước vào giai đoạn tiếp theo của giải đấu danh giá này.
Trong tháng này, các trận đấu vòng sơ loại sẽ diễn ra theo lịch trình cụ thể như sau:
- Vòng sơ loại thứ ba: Diễn ra vào ngày 6-7 tháng 8 (lượt đi) và ngày 13-14 tháng 8 (lượt về). Đây là vòng đấu quy tụ nhiều đội bóng mạnh từ các quốc gia có thứ hạng cao trong hệ số UEFA.
- Vòng play-off: Diễn ra vào ngày 20-21 tháng 8 (lượt đi) và ngày 27-28 tháng 8 (lượt về). Các đội chiến thắng ở vòng này sẽ chính thức giành vé vào vòng bảng UEFA Champions League 2024-2025.
Đáng chú ý trong tháng này, người hâm mộ sẽ được chứng kiến những màn đối đầu nảy lửa giữa các đội bóng đến từ các giải đấu hàng đầu châu Âu như Premier League, La Liga, Bundesliga, Serie A và Ligue 1. Đây là cơ hội để các đội bóng khẳng định mình và giành tấm vé danh giá vào vòng bảng, nơi mà những siêu sao hàng đầu thế giới sẽ tiếp tục tranh tài.
Bên cạnh đó, các trận đấu play-off hứa hẹn mang đến những cuộc so tài hấp dẫn với sự tham gia của các đội bóng như Ajax, Benfica, và Celtic, những đội bóng luôn có truyền thống mạnh mẽ tại đấu trường châu lục.
Người hâm mộ bóng đá không nên bỏ lỡ bất kỳ trận đấu nào trong giai đoạn này, bởi mỗi trận đấu đều là một cuộc chiến khốc liệt quyết định tấm vé vào vòng bảng Cúp C1 Châu Âu mùa giải 2024-2025.

7. Lịch Thi Đấu Các Giải Quốc Gia Khác
Tháng 8 là thời điểm các giải VĐQG trên khắp châu Âu và thế giới bắt đầu sôi động trở lại. Dưới đây là lịch thi đấu của một số giải VĐQG nổi bật ngoài 5 giải đấu lớn:
- Giải VĐQG Bồ Đào Nha (Primeira Liga):
- Giải VĐQG Hà Lan (Eredivisie):
- Giải VĐQG Nga (Russian Premier League):
- Giải VĐQG Bỉ (Belgian Pro League):
- Giải VĐQG Thổ Nhĩ Kỳ (Süper Lig):
Tháng 8 đánh dấu sự khởi động của Primeira Liga, nơi các đội bóng như FC Porto, Benfica, và Sporting CP sẽ tranh tài để giành ngôi vị quán quân. Các trận đấu đáng chú ý bao gồm cuộc đối đầu giữa Benfica và FC Porto vào cuối tháng.
Eredivisie cũng trở lại với những trận cầu sôi động. Ajax, PSV Eindhoven, và Feyenoord là những đội bóng mạnh mẽ nhất của giải đấu, với lịch thi đấu dày đặc trong tháng 8. Trận đấu giữa Ajax và PSV Eindhoven hứa hẹn sẽ là điểm nhấn lớn.
Giải đấu này sẽ chứng kiến các đội bóng như Zenit Saint Petersburg, CSKA Moscow, và Spartak Moscow cạnh tranh gay gắt. Zenit Saint Petersburg, nhà đương kim vô địch, sẽ có một loạt trận đấu quan trọng vào tháng 8.
Trong tháng 8, các trận đấu giữa Club Brugge, Anderlecht, và KRC Genk sẽ thu hút nhiều sự chú ý. Club Brugge, với lịch thi đấu khá thuận lợi, sẽ cố gắng giữ vững ngôi đầu bảng.
Galatasaray, Fenerbahçe và Beşiktaş là những ứng viên nặng ký của Süper Lig mùa này. Các trận đấu giữa những đội bóng này vào tháng 8 sẽ rất đáng xem, đặc biệt là trận derby giữa Fenerbahçe và Galatasaray.
Bên cạnh đó, người hâm mộ cũng có thể theo dõi các giải VĐQG khác như Giải VĐQG Scotland, Giải VĐQG Áo, và Giải VĐQG Ukraine. Mỗi giải đấu đều có những trận cầu hấp dẫn, hứa hẹn mang lại những trải nghiệm bóng đá đầy kịch tính cho khán giả.

8. Lịch Thi Đấu Đội Tuyển Việt Nam
Trong tháng 8 và đầu tháng 9 năm 2024, Đội tuyển bóng đá Việt Nam sẽ có những trận đấu đáng chú ý tại giải giao hữu quốc tế LPBank Cup, nơi đội tuyển sẽ đối đầu với các đối thủ mạnh như Nga và Thái Lan. Đây là cơ hội để đội tuyển thể hiện khả năng và rèn luyện trước thềm các giải đấu lớn sắp tới.
Lịch thi đấu cụ thể của Đội tuyển Việt Nam:
- Ngày 5/9/2024, 20:00: Việt Nam vs Nga
- Ngày 10/9/2024, 20:00: Việt Nam vs Thái Lan
Các trận đấu này sẽ diễn ra tại Sân vận động Quốc gia Mỹ Đình và được truyền hình trực tiếp trên kênh FPT Play. Đây là một chuỗi trận đấu hứa hẹn nhiều cảm xúc, khi Đội tuyển Việt Nam sẽ đối mặt với những đối thủ có sức mạnh vượt trội, tạo cơ hội để các cầu thủ kiểm chứng sức mạnh và chiến thuật của mình trước sự ủng hộ nhiệt tình của khán giả nhà.
XEM THÊM:
9. Lịch Thi Đấu Bóng Đá Nữ
Trong tháng 8, đội tuyển bóng đá nữ Việt Nam sẽ tiếp tục tham gia nhiều giải đấu quốc tế quan trọng, bao gồm vòng loại thứ hai Olympic Paris 2024 và các trận đấu giao hữu quốc tế. Đây là thời điểm quan trọng để đội tuyển nữ thể hiện phong độ và cải thiện vị trí trên bảng xếp hạng FIFA.
Lịch Thi Đấu Vòng Loại Thứ Hai Olympic Paris 2024
- Việt Nam vs Uzbekistan: 19h00 ngày 26/10
- Ấn Độ vs Việt Nam: 17h00 ngày 29/10
- Nhật Bản vs Việt Nam: 17h00 ngày 1/11
Đây là những trận đấu quyết định trong bảng C, nơi đội tuyển Việt Nam phải đối đầu với các đối thủ mạnh như Nhật Bản và Uzbekistan. Mục tiêu của đội là giành vé vào vòng bảng Olympic Paris 2024, một thử thách không hề dễ dàng.
Trận Đấu Giao Hữu Quốc Tế
Để chuẩn bị tốt nhất cho vòng loại Olympic, đội tuyển nữ Việt Nam sẽ tham gia một số trận đấu giao hữu quốc tế nhằm rèn luyện kỹ năng và chiến thuật. Các trận đấu này sẽ là cơ hội để HLV Mai Đức Chung thử nghiệm đội hình và cải thiện khả năng phối hợp của các cầu thủ.
Những Trận Đấu Then Chốt
Trong quá trình chuẩn bị, những trận đấu với các đối thủ mạnh sẽ giúp đội tuyển nữ đánh giá được sức mạnh và khả năng của mình trước khi bước vào vòng loại. Đội tuyển sẽ cần phải chắt chiu từng cơ hội và duy trì tinh thần chiến đấu cao nhất.
Thành Tích Đáng Chú Ý
Đội tuyển nữ Việt Nam đã có nhiều tiến bộ vượt bậc trong thời gian qua, đặc biệt là sau khi giành quyền tham dự World Cup 2023. Đội hình hiện tại đang rất đồng đều và sẵn sàng chinh phục các thử thách mới, với sự dẫn dắt của những cầu thủ kỳ cựu như Huỳnh Như và Chương Thị Kiều.
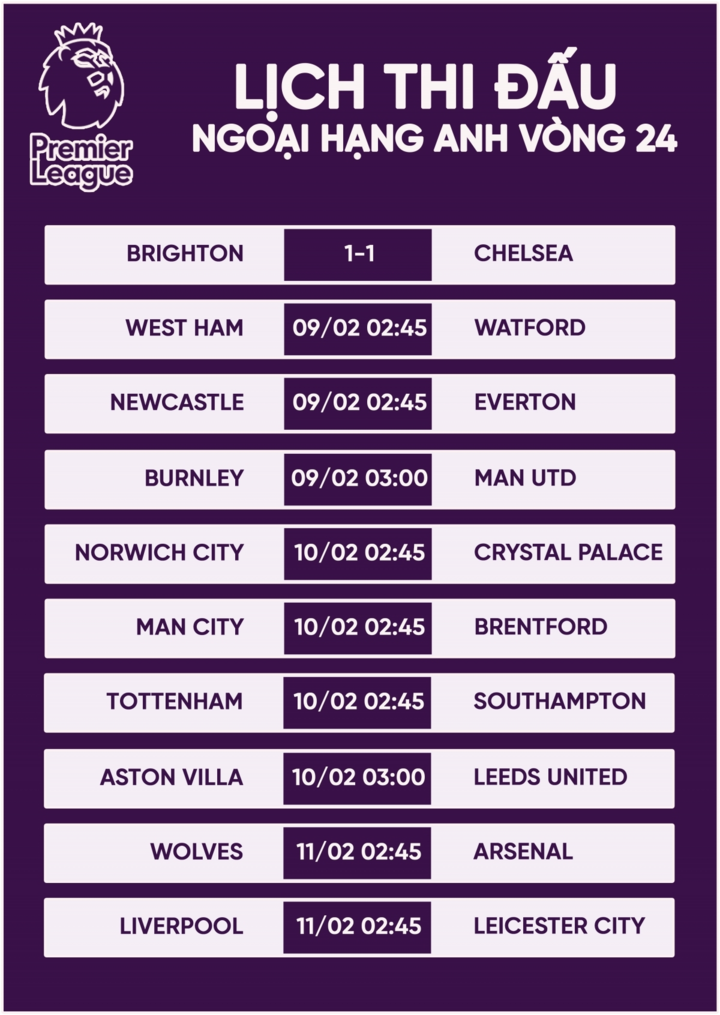
10. Lịch Thi Đấu Các Giải Trẻ
Tháng 8 này, bóng đá trẻ Việt Nam sẽ chứng kiến những trận đấu hấp dẫn và quan trọng, đặc biệt là các giải đấu dành cho lứa U16 và U19. Đây là cơ hội quý báu để các cầu thủ trẻ thể hiện tài năng và rèn luyện kinh nghiệm thi đấu quốc tế. Dưới đây là lịch thi đấu chi tiết của một số giải trẻ:
- Giải U16 Peace Cup 2024:
- Ngày 23/08: U16 Việt Nam vs U16 Hàn Quốc
- Ngày 25/08: U16 Việt Nam vs U16 Nhật Bản
- Ngày 27/08: U16 Việt Nam vs U16 Trung Quốc
Giải đấu này là bước đệm quan trọng cho đội tuyển U16 Việt Nam chuẩn bị cho vòng loại U17 châu Á 2025 diễn ra vào tháng 10 tới.
- Giải U19 Quốc gia 2024:
- Ngày 05/08: U19 Hà Nội vs U19 PVF
- Ngày 10/08: U19 SHB Đà Nẵng vs U19 Bình Dương
- Ngày 15/08: U19 Hoàng Anh Gia Lai vs U19 Sài Gòn
Giải đấu hứa hẹn sẽ mang đến những cuộc tranh tài nảy lửa, nơi các tài năng trẻ có cơ hội phát triển và khẳng định bản thân.
- Giải Hạng Nhì Quốc Gia 2024:
- Ngày 12/08: Trẻ Hà Nội vs Đắk Lắk
- Ngày 19/08: Trẻ TP.HCM vs Lâm Đồng
- Ngày 26/08: Bắc Ninh vs Trẻ SHB Đà Nẵng
Giải Hạng Nhì Quốc Gia cũng là sân chơi để các cầu thủ trẻ thể hiện khả năng trước khi bước vào những sân chơi lớn hơn.
Đây là một mùa giải đầy hứa hẹn cho bóng đá trẻ Việt Nam, với hy vọng những cầu thủ tài năng sẽ trưởng thành và đóng góp cho nền bóng đá nước nhà trong tương lai.

11. Bài Tập Toán: Giải Hệ Phương Trình
Giải hệ phương trình là một phần quan trọng trong toán học, đặc biệt là trong các kỳ thi. Dưới đây là một số bài tập giải hệ phương trình từ cơ bản đến nâng cao.
Bài Tập 1: Hệ Phương Trình Tuyến Tính 2 Ẩn
Giải hệ phương trình sau:
Hướng dẫn giải:
- Bước 1: Giải phương trình thứ nhất để tìm biểu thức của \(y\) theo \(x\).
- Bước 2: Thay giá trị \(y\) vào phương trình thứ hai để tìm giá trị của \(x\).
- Bước 3: Thay giá trị của \(x\) vào phương trình \(y\) đã tìm ở bước 1 để tìm giá trị của \(y\).
- Kết quả: \(x = 2\), \(y = 3\).
Bài Tập 2: Hệ Phương Trình Bậc Hai
Giải hệ phương trình sau:
Hướng dẫn giải:
- Bước 1: Giải phương trình thứ hai để tìm \(x\) theo \(y\).
- Bước 2: Thay giá trị của \(x\) vào phương trình thứ nhất và giải phương trình bậc hai thu được để tìm \(y\).
- Bước 3: Thay giá trị \(y\) đã tìm được vào phương trình thứ hai để tìm \(x\).
- Kết quả: Có hai cặp nghiệm \(x = 4, y = 1\) và \(x = -4, y = -1\).
Bài Tập 3: Hệ Phương Trình Đối Xứng
Giải hệ phương trình sau:
Hướng dẫn giải:
- Bước 1: Sử dụng định lý Viète để biểu diễn tổng và tích các nghiệm.
- Bước 2: Áp dụng phương pháp đại số để biến đổi hệ phương trình.
- Bước 3: Giải các phương trình phụ thu được để tìm các giá trị của \(x\), \(y\), và \(z\).
- Kết quả: \(x = 1\), \(y = 1\), \(z = -1\).
12. Bài Tập Lý: Động Lực Học Chất Điểm
Động lực học chất điểm là một phần quan trọng trong chương trình vật lý, liên quan đến việc phân tích chuyển động của các đối tượng. Để giúp bạn hiểu rõ hơn về chủ đề này, dưới đây là một số bài tập cơ bản kèm theo hướng dẫn giải chi tiết.
12.1. Bài Tập 1: Xác Định Gia Tốc
Cho một vật có khối lượng \( m = 5 \, \text{kg} \) chuyển động với lực tác dụng \( F = 20 \, \text{N} \). Hãy tính gia tốc \( a \) của vật.
- Bước 1: Áp dụng định luật II Newton: \[ F = ma \]
- Bước 2: Tính toán gia tốc: \[ a = \frac{F}{m} = \frac{20 \, \text{N}}{5 \, \text{kg}} = 4 \, \text{m/s}^2 \]
- Kết quả: Gia tốc của vật là \( 4 \, \text{m/s}^2 \).
12.2. Bài Tập 2: Phân Tích Chuyển Động Trên Mặt Phẳng Nghiêng
Một vật có khối lượng \( m = 10 \, \text{kg} \) được đặt trên một mặt phẳng nghiêng góc \( \theta = 30^\circ \) so với phương ngang. Hệ số ma sát giữa vật và mặt phẳng là \( \mu = 0.2 \). Hãy tính gia tốc của vật khi nó bắt đầu trượt xuống.
- Bước 1: Phân tích các lực tác dụng lên vật: trọng lực, lực ma sát, và lực pháp tuyến.
- Bước 2: Áp dụng định luật II Newton theo phương song song với mặt phẳng nghiêng:
- Lực kéo: \( F_k = mg \sin \theta \)
- Lực ma sát: \( F_m = \mu mg \cos \theta \)
- Gia tốc: \[ a = \frac{F_k - F_m}{m} = g(\sin \theta - \mu \cos \theta) \]
- Bước 3: Tính toán: \[ a = 9.8 \, \text{m/s}^2 (\sin 30^\circ - 0.2 \cos 30^\circ) \approx 2.94 \, \text{m/s}^2 \]
- Kết quả: Gia tốc của vật khi trượt xuống là \( 2.94 \, \text{m/s}^2 \).
12.3. Bài Tập 3: Chuyển Động Tròn
Một vật có khối lượng \( m = 2 \, \text{kg} \) chuyển động tròn đều với bán kính \( r = 0.5 \, \text{m} \) và tốc độ góc \( \omega = 4 \, \text{rad/s} \). Hãy tính lực hướng tâm tác dụng lên vật.
- Bước 1: Áp dụng công thức lực hướng tâm: \[ F_{ht} = m \omega^2 r \]
- Bước 2: Tính toán lực hướng tâm: \[ F_{ht} = 2 \, \text{kg} \times (4 \, \text{rad/s})^2 \times 0.5 \, \text{m} = 16 \, \text{N} \]
- Kết quả: Lực hướng tâm tác dụng lên vật là \( 16 \, \text{N} \).
Những bài tập trên giúp bạn củng cố kiến thức về động lực học chất điểm, đồng thời rèn luyện kỹ năng giải quyết các vấn đề liên quan đến lực và chuyển động. Hãy thực hành nhiều hơn để nắm vững kiến thức này.

13. Bài Tập Toán: Tích Phân Bất Định
Tích phân bất định là một phần quan trọng trong giải tích, giúp tìm hiểu nguyên hàm của các hàm số. Dưới đây là một số bài tập cơ bản về tích phân bất định kèm theo hướng dẫn giải chi tiết.
13.1. Bài Tập 1: Tìm Nguyên Hàm Của Hàm Số Đơn Giản
Tìm tích phân bất định của hàm số \( f(x) = 2x + 3 \).
- Bước 1: Áp dụng công thức cơ bản của tích phân: \(\int f(x) \, dx = F(x) + C\), trong đó \( C \) là hằng số tích phân.
- Bước 2: Tính toán tích phân: \[ \int (2x + 3) \, dx = \int 2x \, dx + \int 3 \, dx \]
- Bước 3: Tìm nguyên hàm: \[ F(x) = x^2 + 3x + C \]
- Kết quả: Tích phân bất định của hàm số \( f(x) \) là \( x^2 + 3x + C \).
13.2. Bài Tập 2: Tích Phân Hàm Số Mũ
Tìm tích phân bất định của hàm số \( f(x) = e^{2x} \).
- Bước 1: Áp dụng công thức tích phân: \(\int e^{ax} \, dx = \frac{1}{a}e^{ax} + C\).
- Bước 2: Tính tích phân: \[ \int e^{2x} \, dx = \frac{1}{2}e^{2x} + C \]
- Kết quả: Tích phân bất định của hàm số \( f(x) = e^{2x} \) là \( \frac{1}{2}e^{2x} + C \).
13.3. Bài Tập 3: Tích Phân Hàm Số Lượng Giác
Tìm tích phân bất định của hàm số \( f(x) = \sin(x) + \cos(x) \).
- Bước 1: Sử dụng công thức tích phân của các hàm số lượng giác: \(\int \sin(x) \, dx = -\cos(x) + C\) và \(\int \cos(x) \, dx = \sin(x) + C\).
- Bước 2: Tính toán tích phân: \[ \int (\sin(x) + \cos(x)) \, dx = -\cos(x) + \sin(x) + C \]
- Kết quả: Tích phân bất định của hàm số \( f(x) \) là \( -\cos(x) + \sin(x) + C \).
Các bài tập trên giúp bạn làm quen với phương pháp tính tích phân bất định cho các hàm số cơ bản. Hãy luyện tập nhiều hơn để nâng cao kỹ năng của mình trong việc giải quyết các bài toán tích phân.
14. Bài Tập Lý: Điện Tích và Điện Trường
Trong chương Điện Tích và Điện Trường, chúng ta sẽ tìm hiểu và áp dụng các công thức để giải quyết các bài tập liên quan đến điện tích, điện trường, và lực tương tác giữa các điện tích. Dưới đây là một số bài tập cụ thể để bạn luyện tập.
-
Bài 1: Hai điện tích điểm \( q_1 = 3 \, \mu C \) và \( q_2 = -5 \, \mu C \) đặt cách nhau một khoảng \( r = 2 \, m \) trong chân không. Tính lực tương tác giữa hai điện tích này.
Hướng dẫn:
Áp dụng công thức lực Coulomb:
\[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Với \( k = 9 \times 10^9 \, N \cdot m^2 / C^2 \), bạn có thể thay số vào để tính lực \( F \).
-
Bài 2: Điện tích \( q_1 \) đặt tại gốc tọa độ, điện tích \( q_2 \) đặt tại điểm \( (1, 0, 0) \), và điện tích \( q_3 \) đặt tại điểm \( (0, 1, 0) \). Biết \( q_1 = 2 \, \mu C \), \( q_2 = -1 \, \mu C \), và \( q_3 = 4 \, \mu C \). Hãy tính điện trường tại điểm \( (0, 0, 1) \).
Hướng dẫn:
Sử dụng nguyên lý chồng chất điện trường:
\[ \vec{E} = \vec{E_1} + \vec{E_2} + \vec{E_3} \]Tính từng điện trường \( \vec{E_1}, \vec{E_2}, \vec{E_3} \) rồi cộng chúng lại để có được kết quả cuối cùng.
-
Bài 3: Một điện tích điểm \( q = 1 \, C \) di chuyển dọc theo trục \( x \) trong một điện trường đều \( E = 100 \, N/C \). Tính công mà lực điện trường thực hiện khi điện tích này di chuyển từ \( x = 0 \, m \) đến \( x = 5 \, m \).
Hướng dẫn:
Công của lực điện trường được tính bằng:
\[ A = q \cdot E \cdot d \]Trong đó \( d = x_2 - x_1 = 5 \, m \).
-
Bài 4: Một điện tích \( q = 1 \, \mu C \) được đặt trong điện trường đều có cường độ \( E = 500 \, N/C \). Tính lực điện tác dụng lên điện tích này.
Hướng dẫn:
Áp dụng công thức:
\[ F = q \cdot E \]
Hãy hoàn thành các bài tập trên để củng cố kiến thức về điện tích và điện trường. Chúc bạn học tốt!
15. Bài Tập Tiếng Anh: Chia Thì Động Từ
Kỹ năng chia thì động từ trong tiếng Anh là một trong những kỹ năng cơ bản nhưng vô cùng quan trọng. Để giúp bạn nắm vững và luyện tập, dưới đây là một số dạng bài tập về chia thì động từ. Mỗi dạng bài tập đều được thiết kế để bạn hiểu rõ cách sử dụng và phân biệt các thì khác nhau trong tiếng Anh.
1. Bài tập nhận diện thì động từ
Điền thì đúng của động từ trong ngoặc để hoàn thành các câu sau:
- She (go) to school every day.
- We (watch) a movie last night.
- By the time you arrive, I (finish) my homework.
- They (play) football since 3 PM.
- I (meet) him at the party tomorrow.
2. Bài tập chia thì đúng
Chia động từ trong ngoặc đúng với thì thích hợp:
- I (read) a book when she (call) me.
- She (not/finish) her homework yet.
- They (live) in London for 5 years before moving to New York.
- By next month, we (graduate) from university.
- Look! The cat (chase) a mouse.
3. Bài tập chọn thì phù hợp
Chọn thì đúng để hoàn thành câu:
- When I was young, I (dream) of becoming a teacher.
- She (work) at this company since 2010.
- Tomorrow, we (have) a meeting at 9 AM.
- He usually (play) tennis on Sundays.
- By the time we got to the station, the train (leave).
4. Bài tập viết lại câu
Viết lại các câu sau bằng cách sử dụng thì khác:
- They have already eaten dinner. (Past Simple)
- She was reading a book when I called. (Present Continuous)
- We will go to the concert next week. (Future Perfect)
- He plays football every Sunday. (Past Continuous)
- I had finished my homework before he arrived. (Present Perfect)
5. Bài tập hoàn thành câu
Hoàn thành các câu sau với dạng đúng của động từ trong ngoặc:
- If you (study) hard, you will pass the exam.
- I wish I (know) the answer to this question.
- If it (rain) tomorrow, we will stay at home.
- He (play) guitar since he was a child.
- By next year, I (move) to a new house.

16. Bài Tập Toán: Giải Bất Đẳng Thức
Trong toán học, bất đẳng thức là một khái niệm quan trọng, thường xuyên xuất hiện trong các bài toán từ cơ bản đến nâng cao. Dưới đây là các dạng bài tập và phương pháp giải chi tiết để bạn đọc có thể luyện tập và nâng cao kỹ năng của mình.
16.1. Dạng 1: Bất Đẳng Thức Cơ Bản
Ví dụ: Giải bất đẳng thức sau:
\[
2x - 3 > 5
\]
Giải:
- Thêm 3 vào cả hai vế của bất đẳng thức: \[ 2x - 3 + 3 > 5 + 3 \Rightarrow 2x > 8 \]
- Chia cả hai vế cho 2: \[ \frac{2x}{2} > \frac{8}{2} \Rightarrow x > 4 \]
Vậy nghiệm của bất đẳng thức là \( x > 4 \).
16.2. Dạng 2: Bất Đẳng Thức Có Chứa Ẩn Ở Mẫu
Ví dụ: Giải bất đẳng thức sau:
\[
\frac{3x + 1}{x - 2} \geq 2
\]
Giải:
- Trừ 2 từ cả hai vế và đưa về một mẫu số chung: \[ \frac{3x + 1}{x - 2} - 2 \geq 0 \Rightarrow \frac{3x + 1 - 2(x - 2)}{x - 2} \geq 0 \]
- Rút gọn tử số: \[ \frac{3x + 1 - 2x + 4}{x - 2} \geq 0 \Rightarrow \frac{x + 5}{x - 2} \geq 0 \]
- Xét dấu của biểu thức:
- Tử số \( x + 5 = 0 \) tại \( x = -5 \).
- Mẫu số \( x - 2 = 0 \) tại \( x = 2 \).
- Lập bảng xét dấu và tìm khoảng nghiệm:
Khoảng \( (-\infty, -5) \) \( (-5, 2) \) \( (2, \infty) \) Dấu của \( \frac{x + 5}{x - 2} \) - + - Vậy nghiệm của bất đẳng thức là \( x \in [-5, 2) \).
16.3. Dạng 3: Bất Đẳng Thức Bậc Hai
Ví dụ: Giải bất đẳng thức sau:
\[
x^2 - 5x + 6 \leq 0
\]
Giải:
- Giải phương trình bậc hai tương ứng:
\[
x^2 - 5x + 6 = 0 \Rightarrow (x - 2)(x - 3) = 0
\]
Nghiệm của phương trình là \( x = 2 \) và \( x = 3 \).
- Lập bảng xét dấu và tìm khoảng nghiệm:
Khoảng \( (-\infty, 2) \) \( [2, 3] \) \( (3, \infty) \) Dấu của \( x^2 - 5x + 6 \) + - + Vậy nghiệm của bất đẳng thức là \( x \in [2, 3] \).
16.4. Luyện Tập
Hãy giải các bài tập sau để củng cố kiến thức:
- Giải bất đẳng thức: \[4x - 7 < 9\]
- Giải bất đẳng thức: \[\frac{5x + 2}{x - 1} \leq 3\]
- Giải bất đẳng thức: \[x^2 - 4x - 5 > 0\]
17. Bài Tập Lý: Nhiệt Học
Nhiệt học là một phân môn quan trọng trong vật lý, nghiên cứu về các hiện tượng liên quan đến nhiệt độ, nhiệt năng, và quá trình truyền nhiệt. Dưới đây là một số bài tập liên quan đến chủ đề này.
Bài 1: Xác định nhiệt lượng
Một thanh sắt có khối lượng \(m = 2 \, kg\) được nung nóng từ \(20^\circ C\) lên \(100^\circ C\). Xác định nhiệt lượng cần thiết để thực hiện quá trình này, biết nhiệt dung riêng của sắt là \(c = 460 \, J/(kg \cdot K)\).
- Phương trình tính nhiệt lượng: \[ Q = m \cdot c \cdot \Delta T \]
- Trong đó:
- \(Q\): Nhiệt lượng cần truyền vào (J)
- \(m\): Khối lượng vật (kg)
- \(c\): Nhiệt dung riêng của vật liệu (J/(kg·K))
- \(\Delta T\): Độ biến thiên nhiệt độ (\(K\))
- Thay số: \[ Q = 2 \times 460 \times (100 - 20) = 73600 \, J \]
Bài 2: Truyền nhiệt giữa hai vật
Một thanh đồng và một thanh nhôm có khối lượng lần lượt là \(m_1 = 1 \, kg\) và \(m_2 = 1.5 \, kg\), được nung nóng đến nhiệt độ ban đầu là \(T_1 = 80^\circ C\) và \(T_2 = 20^\circ C\). Khi đặt chúng tiếp xúc với nhau, nhiệt độ cuối cùng của hệ là \(T = 50^\circ C\). Xác định nhiệt dung riêng của nhôm biết nhiệt dung riêng của đồng là \(c_1 = 390 \, J/(kg \cdot K)\).
- Phương trình cân bằng nhiệt: \[ m_1 \cdot c_1 \cdot (T_1 - T) = m_2 \cdot c_2 \cdot (T - T_2) \]
- Thay số và giải phương trình để tìm \(c_2\) (nhiệt dung riêng của nhôm).
Bài 3: Quá trình nhiệt động lực học
Một hệ khí lý tưởng được giữ trong bình có dung tích cố định. Nhiệt độ của khí tăng từ \(T_1 = 300 \, K\) lên \(T_2 = 600 \, K\). Xác định sự biến thiên năng lượng nội của hệ khí, biết rằng khí là đơn nguyên tử và có số mol \(n = 2 \, mol\).
- Phương trình năng lượng nội: \[ \Delta U = \frac{3}{2} \cdot n \cdot R \cdot \Delta T \]
- Trong đó:
- \(\Delta U\): Sự biến thiên năng lượng nội (J)
- \(n\): Số mol khí (mol)
- \(R\): Hằng số khí lý tưởng (\(8.314 \, J/(mol \cdot K)\))
- \(\Delta T\): Độ biến thiên nhiệt độ (\(K\))
- Thay số và tính toán \(\Delta U\).
Các bài tập trên sẽ giúp bạn nắm vững hơn về các khái niệm cơ bản trong nhiệt học và áp dụng chúng vào việc giải quyết các bài toán thực tế.
18. Bài Tập Tiếng Anh: Câu Điều Kiện
Câu điều kiện là một phần quan trọng trong ngữ pháp tiếng Anh, thường được sử dụng để diễn tả một điều kiện và kết quả của điều kiện đó. Bài tập này sẽ giúp bạn ôn tập và nắm vững các loại câu điều kiện, từ cơ bản đến nâng cao.
Loại 1: Câu Điều Kiện Loại 0
Câu điều kiện loại 0 diễn tả một sự thật hiển nhiên, một sự việc luôn luôn đúng.
- Cấu trúc: If + S + V (hiện tại đơn), S + V (hiện tại đơn)
- Ví dụ: If you heat water to 100°C, it boils. (Nếu bạn đun nước đến 100°C, nó sẽ sôi.)
Loại 2: Câu Điều Kiện Loại 1
Câu điều kiện loại 1 diễn tả một điều kiện có thật ở hiện tại hoặc tương lai và kết quả có thể xảy ra.
- Cấu trúc: If + S + V (hiện tại đơn), S + will + V (nguyên mẫu)
- Ví dụ: If it rains tomorrow, we will stay at home. (Nếu ngày mai trời mưa, chúng tôi sẽ ở nhà.)
Loại 3: Câu Điều Kiện Loại 2
Câu điều kiện loại 2 dùng để nói về những điều kiện không có thật ở hiện tại hoặc tương lai và kết quả giả định.
- Cấu trúc: If + S + V (quá khứ đơn), S + would + V (nguyên mẫu)
- Ví dụ: If I were you, I would study harder. (Nếu tôi là bạn, tôi sẽ học chăm chỉ hơn.)
Loại 4: Câu Điều Kiện Loại 3
Câu điều kiện loại 3 diễn tả một điều kiện không có thật trong quá khứ và kết quả không có thật trong quá khứ.
- Cấu trúc: If + S + had + V3/ed, S + would have + V3/ed
- Ví dụ: If I had known about the meeting, I would have attended it. (Nếu tôi biết về cuộc họp, tôi đã tham dự nó.)
Bài Tập Thực Hành
- Điền từ thích hợp vào chỗ trống: If I _______ (have) time, I would travel more.
- Chuyển câu sau sang dạng điều kiện loại 3: He didn't pass the exam because he didn't study hard.
- Viết lại câu sau sử dụng câu điều kiện loại 1: You don’t water the plants, so they die.
Hãy làm những bài tập này để củng cố kiến thức và gửi lại cho giáo viên của bạn để được nhận xét và chấm điểm.

19. Bài Tập Toán: Đạo Hàm và Ứng Dụng
Đạo hàm là một khái niệm cơ bản trong toán học, đặc biệt trong giải tích, được sử dụng để tìm tốc độ thay đổi của một hàm số. Bài tập này sẽ giúp bạn củng cố kiến thức về đạo hàm và cách ứng dụng nó trong việc giải các bài toán thực tế.
1. Tính Đạo Hàm Của Hàm Số
Hãy tính đạo hàm của các hàm số sau:
- \[ f(x) = 3x^2 + 5x - 7 \]
- \[ g(x) = \sin(x) + \cos(x) \]
- \[ h(x) = e^x \cdot \ln(x) \]
Gợi ý: Sử dụng các quy tắc đạo hàm cơ bản như quy tắc tổng, quy tắc nhân, và quy tắc chuỗi.
2. Ứng Dụng Của Đạo Hàm Trong Việc Tìm Cực Trị
Hãy tìm các điểm cực trị của hàm số sau và xác định loại cực trị (cực đại, cực tiểu hay điểm yên ngựa):
- \[ f(x) = x^3 - 6x^2 + 9x + 2 \]
Gợi ý: Tính đạo hàm bậc nhất để tìm các điểm có đạo hàm bằng 0, sau đó sử dụng đạo hàm bậc hai để xác định loại cực trị.
3. Tính Đạo Hàm Của Hàm Số Ẩn
Cho phương trình \[ x^2 + y^2 = 1 \], hãy tính \(\frac{dy}{dx}\).
Gợi ý: Sử dụng phương pháp đạo hàm ẩn để giải quyết bài toán này.
4. Ứng Dụng Của Đạo Hàm Trong Tính Tốc Độ Thay Đổi
Một chiếc xe đang di chuyển theo đường thẳng với phương trình quãng đường \[ s(t) = t^3 - 6t^2 + 9t + 4 \] (trong đó \(s\) tính bằng mét và \(t\) tính bằng giây). Hãy tính tốc độ và gia tốc của xe tại thời điểm \(t = 2\) giây.
Gợi ý: Tốc độ là đạo hàm bậc nhất của hàm số \(s(t)\), còn gia tốc là đạo hàm bậc hai của \(s(t)\).
5. Bài Toán Thực Tế Về Đạo Hàm
Một doanh nghiệp sản xuất có hàm chi phí \(C(x) = 100 + 5x - 0.01x^2\), trong đó \(x\) là số lượng sản phẩm sản xuất. Hãy tìm số lượng sản phẩm mà chi phí biên là nhỏ nhất.
Gợi ý: Tính đạo hàm của hàm chi phí để tìm hàm chi phí biên, sau đó tìm giá trị \(x\) tối ưu.
Hãy thực hiện các bài tập trên và kiểm tra kết quả của bạn để nắm vững hơn về khái niệm đạo hàm và ứng dụng của nó trong các bài toán thực tế.
20. Bài Tập Lý: Từ Trường và Ứng Dụng
Bài tập 1: Tính cường độ từ trường của dòng điện
- Một dây dẫn thẳng dài mang dòng điện \( I = 10A \). Tính cường độ từ trường \( B \) tại một điểm cách dây dẫn một khoảng \( r = 0.2m \).
Giải:
Công thức tính cường độ từ trường của dòng điện thẳng dài là:
\[ B = \frac{\mu_0 I}{2\pi r} \]
Với:
- \(\mu_0\): Hằng số từ trường trong chân không, \(\mu_0 = 4\pi \times 10^{-7} T\cdot m/A \)
- I: Cường độ dòng điện (A)
- r: Khoảng cách từ dây dẫn đến điểm cần tính (m)
Thay số vào công thức:
\[ B = \frac{4\pi \times 10^{-7} \times 10}{2\pi \times 0.2} = 1 \times 10^{-5} T \]
Vậy cường độ từ trường tại điểm cách dây dẫn 0.2m là \( 10^{-5} T \).
Bài tập 2: Lực từ tác dụng lên đoạn dây dẫn mang dòng điện
- Một đoạn dây dẫn dài 0.5m mang dòng điện \( I = 2A \) được đặt trong từ trường đều có cường độ \( B = 0.01T \). Tính lực từ tác dụng lên đoạn dây dẫn nếu dây vuông góc với từ trường.
Giải:
Công thức tính lực từ là:
\[ F = BIL \sin\theta \]
Với:
- B: Cường độ từ trường (T)
- I: Cường độ dòng điện (A)
- L: Chiều dài đoạn dây dẫn (m)
- \(\theta\): Góc giữa dây dẫn và từ trường, ở đây \(\theta = 90^\circ\), do đó \(\sin\theta = 1\)
Thay số vào công thức:
\[ F = 0.01 \times 2 \times 0.5 \times 1 = 0.01N \]
Vậy lực từ tác dụng lên đoạn dây dẫn là 0.01N.
Bài tập 3: Ứng dụng của từ trường trong động cơ điện
- Trình bày nguyên lý hoạt động của động cơ điện một chiều và vai trò của từ trường trong động cơ này.
Giải:
Động cơ điện một chiều hoạt động dựa trên nguyên lý lực từ tác dụng lên đoạn dây dẫn mang dòng điện đặt trong từ trường. Khi dòng điện chạy qua cuộn dây trong từ trường, lực từ sẽ tác dụng lên cuộn dây, làm cho nó quay. Chuyển động quay của cuộn dây được truyền ra ngoài qua trục quay, tạo thành cơ năng.
Từ trường đóng vai trò quan trọng trong việc tạo ra lực từ để làm quay cuộn dây, giúp chuyển đổi năng lượng điện thành cơ năng.