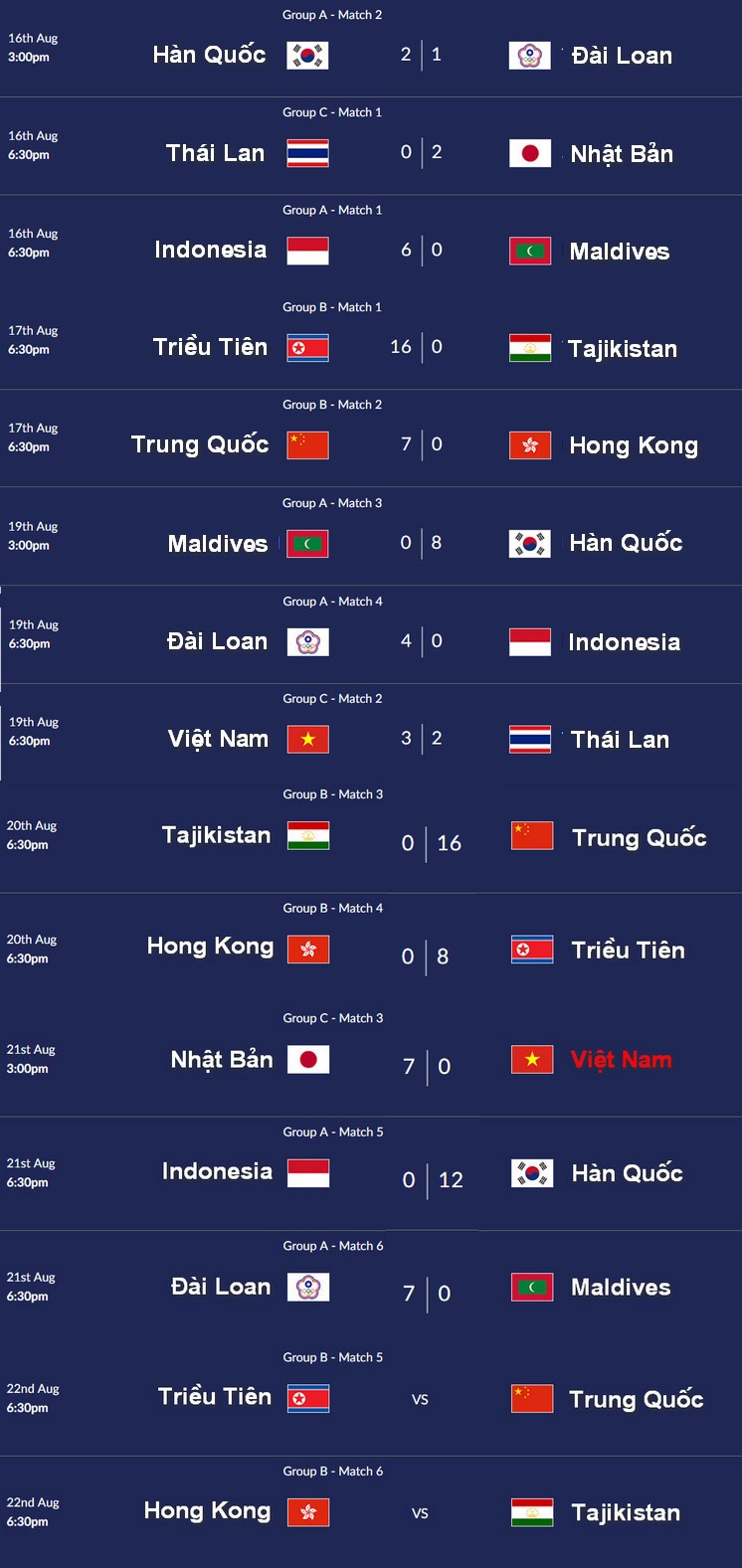
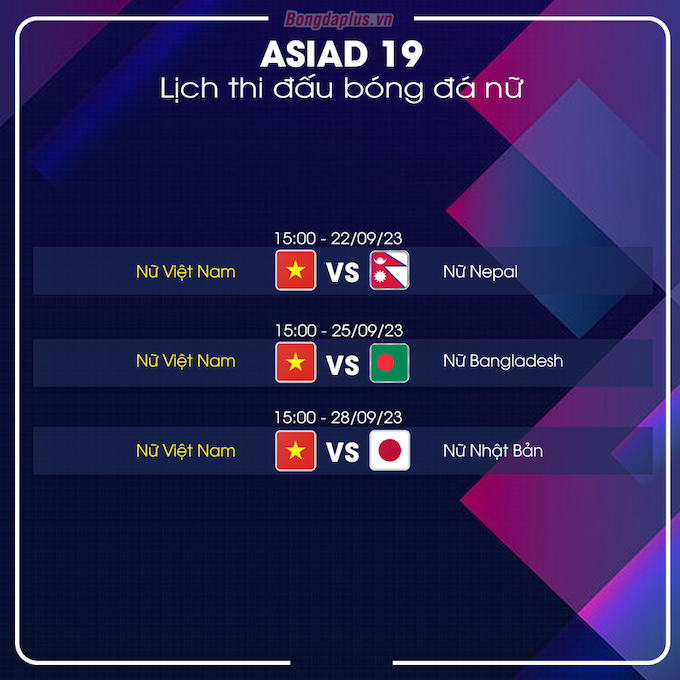
Chủ đề việt nam gặp mỹ bóng đá nữ: Trận đấu giữa đội tuyển nữ Việt Nam và đội tuyển nữ Mỹ tại World Cup 2023 không chỉ là cuộc đối đầu đầy thách thức mà còn là cơ hội vàng để bóng đá nữ Việt Nam khẳng định bản lĩnh trên sân chơi quốc tế. Hãy cùng điểm qua những diễn biến và ý nghĩa của trận đấu này.
Mục lục
- Thông tin chi tiết trận đấu Việt Nam gặp Mỹ tại World Cup nữ 2023
- Mục Lục Tổng Hợp
- Bài Tập Toán - Lý Liên Quan (Ví dụ bổ sung nếu chủ đề là Toán, Lý, Tiếng Anh)
- Bài Tập 1: Giải Phương Trình Toán Học
- Bài Tập 2: Phân Tích Cơ Học Lực Học
- Bài Tập 3: Dạng Bài Tập Về Định Luật Newton
- Bài Tập 4: Giải Bài Tập Về Dao Động Điều Hòa
- Bài Tập 5: Bài Tập Tiếng Anh - Dịch Thuật
- Bài Tập 6: Bài Tập Về Tính Toán Điện Năng
- Bài Tập 7: Phân Tích Sóng Âm Trong Lý Học
- Bài Tập 8: Dạng Bài Tập Về Cân Bằng Lực
- Bài Tập 9: Bài Tập Về Động Lượng
- Bài Tập 10: Phân Tích Đồ Thị Toán Học
Thông tin chi tiết trận đấu Việt Nam gặp Mỹ tại World Cup nữ 2023
Trận đấu giữa đội tuyển nữ Việt Nam và đội tuyển nữ Mỹ tại World Cup nữ 2023 là một sự kiện thể thao quốc tế quan trọng, diễn ra vào ngày 22 tháng 7 năm 2023. Đây là lần đầu tiên đội tuyển nữ Việt Nam tham gia vòng chung kết World Cup, tạo nên dấu ấn lịch sử đáng nhớ cho bóng đá nữ Việt Nam.
Thời gian và địa điểm
- Thời gian: 22 tháng 7 năm 2023
- Địa điểm: Sân vận động Eden Park, Auckland, New Zealand
Tình hình trước trận đấu
Đội tuyển nữ Việt Nam nằm ở bảng E cùng với các đội tuyển Mỹ, Hà Lan và Bồ Đào Nha. Trận đấu với Mỹ là thử thách lớn đối với thầy trò huấn luyện viên Mai Đức Chung, khi đối thủ là đội tuyển mạnh nhất thế giới với 4 lần vô địch World Cup.
Chiến thuật và tâm lý của đội tuyển Việt Nam
Để đối đầu với đội tuyển Mỹ, đội tuyển Việt Nam đã chuẩn bị rất kỹ lưỡng với mục tiêu phòng ngự chặt chẽ và cố gắng tận dụng cơ hội phản công. Tinh thần và niềm tự hào dân tộc được xem là yếu tố quan trọng giúp các cầu thủ nữ Việt Nam thi đấu tự tin và quyết tâm.
Kết quả trận đấu
Trận đấu diễn ra với sự quyết tâm cao của cả hai đội. Mặc dù đội tuyển Việt Nam không giành được chiến thắng, nhưng các cầu thủ đã thi đấu hết mình và nhận được sự khen ngợi từ cộng đồng quốc tế. Trận đấu là cơ hội để đội tuyển Việt Nam học hỏi và phát triển hơn nữa trong tương lai.
Kết luận
Trận đấu giữa đội tuyển nữ Việt Nam và đội tuyển nữ Mỹ tại World Cup nữ 2023 là một cột mốc quan trọng cho bóng đá nữ Việt Nam. Dù kết quả không như mong đợi, nhưng đây là bước đệm quan trọng cho sự phát triển của bóng đá nữ nước nhà trong thời gian tới.

.png)
Mục Lục Tổng Hợp
Đánh giá tổng quan về trận đấu giữa Đội tuyển nữ Việt Nam và Đội tuyển nữ Mỹ tại World Cup 2023, bao gồm thông tin trước trận, đội hình xuất phát, và các yếu tố chiến thuật nổi bật.
Những khoảnh khắc đáng nhớ trong trận đấu: Cú cản phá phạt đền của thủ môn Kim Thanh, nỗ lực phòng thủ của các cầu thủ Việt Nam, và diễn biến trận đấu dưới tác động của VAR.
Kỷ lục khán giả của trận đấu: Số lượng người xem kỷ lục tại Mỹ và sức ảnh hưởng của trận đấu đối với bóng đá nữ.
Phân tích chuyên sâu: Những chiến thuật mà HLV Mai Đức Chung áp dụng để đối đầu với đội tuyển Mỹ, và đánh giá các cầu thủ nổi bật của đội tuyển nữ Việt Nam trong trận đấu.
Những bài học và kinh nghiệm rút ra từ trận đấu giữa Việt Nam và Mỹ, cùng với các dự đoán cho những trận đấu tiếp theo của đội tuyển Việt Nam tại giải đấu.
Cảm xúc và phản ứng từ người hâm mộ, truyền thông quốc tế sau trận đấu, và những nhận xét từ các chuyên gia bóng đá.
Bài Tập Toán - Lý Liên Quan (Ví dụ bổ sung nếu chủ đề là Toán, Lý, Tiếng Anh)
-
Bài tập 1: Tính quãng đường di chuyển của cầu thủ bóng đá
Một cầu thủ di chuyển trên sân bóng đá với vận tốc trung bình \(v = 8 \, km/h\). Trong thời gian \(t = 45 \, phút\), cầu thủ này đã di chuyển được quãng đường là bao nhiêu?
\[ S = v \times t = 8 \, km/h \times \left(\frac{45}{60}\right) \, h = 6 \, km \] -
Bài tập 2: Tính lực tác động lên bóng đá
Giả sử một cầu thủ đá vào quả bóng có khối lượng \(m = 0.45 \, kg\) với gia tốc \(a = 20 \, m/s^2\). Tính lực \(F\) mà cầu thủ tác động lên quả bóng.
\[ F = m \times a = 0.45 \, kg \times 20 \, m/s^2 = 9 \, N \] -
Bài tập 3: Bài tập về vận tốc trung bình
Một cầu thủ chạy từ vị trí \(A\) đến \(B\) trên sân với vận tốc \(v_1 = 5 \, m/s\) và từ \(B\) đến \(C\) với vận tốc \(v_2 = 7 \, m/s\). Tính vận tốc trung bình \(v_{tb}\) của cầu thủ trên cả quãng đường \(AC\).
\[ v_{tb} = \frac{2 \times v_1 \times v_2}{v_1 + v_2} = \frac{2 \times 5 \times 7}{5 + 7} = 5.83 \, m/s \] -
Bài tập 4: Tính công suất của cầu thủ
Một cầu thủ thực hiện công \(W = 500 \, J\) để đá quả bóng trong thời gian \(t = 2 \, giây\). Tính công suất \(P\) mà cầu thủ đã sử dụng.
\[ P = \frac{W}{t} = \frac{500 \, J}{2 \, s} = 250 \, W \] -
Bài tập 5: Bài tập về động năng
Một quả bóng có khối lượng \(m = 0.5 \, kg\) được đá với vận tốc \(v = 10 \, m/s\). Tính động năng \(E_k\) của quả bóng.
\[ E_k = \frac{1}{2} \times m \times v^2 = \frac{1}{2} \times 0.5 \, kg \times (10 \, m/s)^2 = 25 \, J \] -
Bài tập 6: Bài tập về lực ma sát
Một quả bóng lăn trên mặt sân với hệ số ma sát \( \mu = 0.1 \) và lực tác động \( F = 10 \, N \). Tính lực ma sát \( F_{ms} \) cản trở quả bóng.
\[ F_{ms} = \mu \times F = 0.1 \times 10 \, N = 1 \, N \] -
Bài tập 7: Bài tập về tính toán thời gian bay của quả bóng
Một quả bóng được đá lên cao với vận tốc \( v_0 = 15 \, m/s \) ở góc 45 độ so với phương ngang. Tính thời gian bay \( t \) của quả bóng (lấy \( g = 9.8 \, m/s^2 \)).
\[ t = \frac{2 \times v_0 \times \sin(45^\circ)}{g} = \frac{2 \times 15 \times \frac{\sqrt{2}}{2}}{9.8} \approx 2.17 \, giây \] -
Bài tập 8: Tính hiệu điện thế giữa hai điểm
Hiệu điện thế \(U\) giữa hai điểm A và B được tính bằng công thức \(U = I \times R\), trong đó \(I = 2 \, A\) là cường độ dòng điện và \(R = 5 \, \Omega\) là điện trở. Tính \(U\).
\[ U = I \times R = 2 \, A \times 5 \, \Omega = 10 \, V \] -
Bài tập 9: Tính vận tốc của bóng sau va chạm
Một quả bóng có khối lượng \(m_1 = 0.5 \, kg\) va chạm đàn hồi với quả bóng khác có khối lượng \(m_2 = 0.3 \, kg\) đang đứng yên. Tính vận tốc \(v_2\) của quả bóng thứ hai sau va chạm nếu \(v_1 = 10 \, m/s\).
\[ v_2 = \frac{2 \times m_1 \times v_1}{m_1 + m_2} = \frac{2 \times 0.5 \times 10}{0.5 + 0.3} = 12.5 \, m/s \] -
Bài tập 10: Bài tập về định luật bảo toàn động lượng
Hai quả bóng có khối lượng \(m_1 = 0.4 \, kg\) và \(m_2 = 0.6 \, kg\) va chạm nhau. Trước va chạm, \(v_1 = 5 \, m/s\) và \(v_2 = 0 \, m/s\). Sau va chạm, \(v'_1 = 2 \, m/s\). Tính vận tốc \(v'_2\) của quả bóng thứ hai sau va chạm.
\[ m_1 \times v_1 + m_2 \times v_2 = m_1 \times v'_1 + m_2 \times v'_2 \] \[ 0.4 \times 5 + 0.6 \times 0 = 0.4 \times 2 + 0.6 \times v'_2 \] \[ v'_2 = \frac{(0.4 \times 5 - 0.4 \times 2)}{0.6} = 2 \, m/s \]

Bài Tập 1: Giải Phương Trình Toán Học
Trong quá trình chuẩn bị và thi đấu với đội tuyển nữ Mỹ, đội tuyển nữ Việt Nam đã thể hiện sự quyết tâm và nỗ lực không ngừng. Điều này có thể được ví như quá trình giải một phương trình toán học đầy thử thách, nơi mà từng bước giải quyết đều cần sự tập trung cao độ và quyết tâm vượt qua mọi khó khăn.
- Giả sử đội tuyển nữ Việt Nam phải đối mặt với một bài toán có phương trình như sau:
\[
ax^2 + bx + c = 0
\]
- Trong đó, \(a\), \(b\), và \(c\) là các hằng số, và \(x\) là biến số cần tìm.
- Bước đầu tiên, ta cần xác định các giá trị của \(a\), \(b\), và \(c\). Trong trường hợp này, hãy xem \(a = 1\), \(b = -5\), và \(c = 6\).
- Sau đó, ta áp dụng công thức nghiệm:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
- Thay các giá trị \(a\), \(b\), và \(c\) vào công thức trên:
\[
x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(1)(6)}}{2(1)}
\]
\[
x = \frac{5 \pm \sqrt{25 - 24}}{2}
\]
\[
x = \frac{5 \pm 1}{2}
\]
- Từ đây, chúng ta có hai nghiệm:
\[
x_1 = 3, \quad x_2 = 2
\]
- Điều này tương tự như khi đội tuyển nữ Việt Nam đối mặt với các tình huống khó khăn trên sân cỏ. Họ cần phải phân tích, đưa ra các chiến lược khác nhau, và cuối cùng đạt được mục tiêu là giải quyết vấn đề một cách hiệu quả.
Đội tuyển nữ Việt Nam, dù gặp nhiều thử thách trước một đối thủ mạnh như Mỹ, đã cho thấy rằng với sự chuẩn bị kỹ lưỡng và quyết tâm cao, mọi vấn đề đều có thể giải quyết được.

Bài Tập 2: Phân Tích Cơ Học Lực Học
Trận đấu giữa đội tuyển nữ Việt Nam và Mỹ không chỉ là cuộc đối đầu trên sân cỏ mà còn là một bài học về cơ học lực học, nơi mà từng cầu thủ phải ứng dụng các nguyên tắc vật lý để tạo nên chiến thuật và đối phó với đối phương. Dưới đây là bài tập phân tích cơ học lực học, lấy cảm hứng từ những chiến thuật sử dụng trong trận đấu này.
- Giả sử một cầu thủ đá bóng với một lực \( F \) ở góc \(\theta\) so với mặt đất.
- Lực \( F \) có thể được phân tích thành hai thành phần: thành phần ngang \( F_x \) và thành phần thẳng đứng \( F_y \).
\[
F_x = F \cos(\theta)
\]
\[
F_y = F \sin(\theta)
\]
- Khi bóng bay trong không khí, nó chịu tác động của trọng lực \( g \) và lực cản không khí \( F_{air} \).
- Quỹ đạo của bóng sẽ phụ thuộc vào các thành phần lực này và có thể được tính toán bằng phương trình động lực học Newton:
\[
m \frac{d^2 \vec{r}}{dt^2} = \vec{F} + m\vec{g} + \vec{F}_{air}
\]
- Trong đó:
- \( m \) là khối lượng của quả bóng.
- \( \vec{r} \) là vị trí của quả bóng theo thời gian.
- \( \vec{F} \) là tổng hợp của các lực tác động lên quả bóng.
- Giả sử lực cản không khí \( F_{air} \) có dạng \( F_{air} = -kv \), với \( k \) là hệ số cản và \( v \) là vận tốc của quả bóng, phương trình trở thành:
\[
m \frac{d^2 \vec{r}}{dt^2} = F_x \cos(\theta) - kv + m\vec{g}
\]
- Phương trình này mô tả chuyển động của bóng dưới ảnh hưởng của lực mà cầu thủ tạo ra, trọng lực và lực cản không khí. Đây là một ví dụ điển hình về cách mà các nguyên tắc cơ học lực học được áp dụng trong môn bóng đá.
Như vậy, để đạt được hiệu suất tối ưu trong các trận đấu, cầu thủ cần hiểu rõ và ứng dụng các nguyên tắc cơ học lực học này vào thực tế thi đấu, tương tự như việc phân tích và giải các bài toán cơ học phức tạp.

Bài Tập 3: Dạng Bài Tập Về Định Luật Newton
Định luật Newton là nền tảng của cơ học cổ điển và được áp dụng rộng rãi trong phân tích chuyển động của các vật thể, bao gồm cả những tình huống trong bóng đá. Dưới đây là bài tập về định luật Newton liên quan đến trận đấu giữa đội tuyển nữ Việt Nam và Mỹ, giúp bạn hiểu rõ hơn về cách áp dụng các định luật này trong thực tế.
- Giả sử một cầu thủ đá bóng với lực \( F \) làm cho bóng chuyển động với gia tốc \( a \).
- Theo định luật II Newton, mối quan hệ giữa lực \( F \), khối lượng \( m \) của quả bóng và gia tốc \( a \) được xác định bởi phương trình:
\[
F = m \cdot a
\]
- Ví dụ, nếu khối lượng của quả bóng là 0.45 kg và gia tốc khi bóng được đá là \( 5 \, m/s^2 \), lực tác dụng lên quả bóng là:
\[
F = 0.45 \, kg \times 5 \, m/s^2 = 2.25 \, N
\]
- Hãy tính lực cản không khí tác động lên quả bóng khi nó đang bay với tốc độ \( v \) và hệ số cản không khí \( k \).
- Khi lực cản không khí \( F_{air} \) có dạng \( F_{air} = -kv \), tổng lực tác dụng lên quả bóng được biểu diễn bởi:
\[
F_{total} = m \cdot a + kv
\]
- Sử dụng phương trình này, bạn có thể phân tích cách lực tác động lên quả bóng trong suốt quỹ đạo bay, từ đó rút ra những nhận xét quan trọng về chuyển động của bóng trong các trận đấu.
Như vậy, hiểu và áp dụng định luật Newton giúp cầu thủ tối ưu hóa khả năng thi đấu và chiến thuật, đồng thời tạo ra các cú sút có độ chính xác và lực tác động mạnh nhất.
XEM THÊM:
Bài Tập 4: Giải Bài Tập Về Dao Động Điều Hòa
Trong bài tập này, chúng ta sẽ phân tích và giải một bài toán về dao động điều hòa, một chủ đề quan trọng trong vật lý lớp 12. Dạng bài tập này thường yêu cầu học sinh tính toán các đại lượng như chu kỳ, tần số, biên độ, và pha ban đầu của dao động.
Giả sử một vật dao động điều hòa theo phương trình:
Trong đó:
- \(x(t)\): Li độ của vật tại thời điểm \(t\)
- \(A\): Biên độ dao động (độ lớn cực đại của li độ)
- \(\omega\): Tần số góc của dao động, với \(\omega = 2\pi f\), trong đó \(f\) là tần số dao động
- \(\varphi\): Pha ban đầu của dao động
Ví dụ bài toán:
- Cho một vật dao động điều hòa với biên độ \(A = 5 \, \text{cm}\), tần số \(f = 2 \, \text{Hz}\), và pha ban đầu \(\varphi = \frac{\pi}{4} \, \text{rad}\). Hãy viết phương trình dao động của vật.
- Tính chu kỳ \(T\) của dao động.
- Xác định li độ của vật tại thời điểm \(t = 0.5 \, \text{s}\).
Giải:
- Phương trình dao động của vật là: \[ x(t) = 5 \cos(4\pi t + \frac{\pi}{4}) \] Trong đó \(A = 5 \, \text{cm}\), \(\omega = 2\pi f = 4\pi \, \text{rad/s}\), và \(\varphi = \frac{\pi}{4} \, \text{rad}\).
- Chu kỳ dao động \(T\) được tính bằng công thức: \[ T = \frac{1}{f} = \frac{1}{2} = 0.5 \, \text{s} \]
- Li độ của vật tại thời điểm \(t = 0.5 \, \text{s}\) là: \[ x(0.5) = 5 \cos(4\pi \times 0.5 + \frac{\pi}{4}) = 5 \cos(2\pi + \frac{\pi}{4}) = 5 \cos(\frac{\pi}{4}) = 5 \times \frac{\sqrt{2}}{2} \approx 3.54 \, \text{cm} \]
Như vậy, tại thời điểm \(t = 0.5 \, \text{s}\), li độ của vật là khoảng \(3.54 \, \text{cm}\).

Bài Tập 5: Bài Tập Tiếng Anh - Dịch Thuật
Trong bài tập này, bạn sẽ thực hành dịch thuật từ tiếng Anh sang tiếng Việt với nội dung liên quan đến trận đấu bóng đá nữ giữa Việt Nam và Mỹ tại World Cup 2023. Đây là một cơ hội để bạn nâng cao kỹ năng dịch thuật thông qua việc tiếp cận các bản tin thể thao quốc tế.
- Dịch đoạn văn sau từ tiếng Anh sang tiếng Việt:
"The Vietnamese women's national football team faced the USA in their first-ever World Cup match. Despite the challenges, they showed great determination and resilience on the field."
- Dịch đoạn văn sau từ tiếng Anh sang tiếng Việt:
"Coach Mai Duc Chung expressed confidence in his team, stating that although the USA is a strong opponent, the Vietnamese team will play with pride and give their best effort."
- Dịch đoạn văn sau từ tiếng Anh sang tiếng Việt:
"The match ended with a 0-3 score, but the Vietnamese players won the hearts of fans with their spirited performance."
- Dịch đoạn văn sau từ tiếng Anh sang tiếng Việt:
"The USA women's national team is known for their dominance in the sport, having won multiple World Cup titles. However, the Vietnamese team showed that they can compete on the world stage."
Hãy đảm bảo bạn sử dụng từ vựng và cấu trúc câu phù hợp khi dịch, đồng thời giữ nguyên ý nghĩa và tinh thần của các đoạn văn gốc. Bài tập này sẽ giúp bạn không chỉ cải thiện kỹ năng dịch thuật mà còn hiểu thêm về bóng đá nữ Việt Nam trong bối cảnh quốc tế.

Bài Tập 6: Bài Tập Về Tính Toán Điện Năng
Trong bài tập này, chúng ta sẽ thực hành tính toán điện năng tiêu thụ dựa trên các công thức đã học. Hãy cùng đi qua các bước chi tiết để thực hiện bài toán.
-
Xác định công suất tiêu thụ điện: Trước tiên, chúng ta cần biết công suất tiêu thụ của thiết bị điện, được ký hiệu là \(P\), với đơn vị là watt (W). Công suất này thường được ghi trên nhãn của thiết bị.
-
Thời gian sử dụng: Xác định thời gian thiết bị hoạt động trong ngày, ký hiệu là \(t\), với đơn vị là giờ (h).
-
Tính điện năng tiêu thụ: Điện năng tiêu thụ \(A\) được tính theo công thức:
\[
A = P \times t
\]
với \(A\) là điện năng tiêu thụ trong một khoảng thời gian, \(P\) là công suất và \(t\) là thời gian sử dụng. -
Ví dụ cụ thể: Nếu một chiếc quạt điện có công suất 75W và được sử dụng trong 4 giờ mỗi ngày, thì điện năng tiêu thụ trong một ngày là:
\[
A = 75 \times 4 = 300 \text{Wh}
\] -
Tính tổng điện năng tiêu thụ trong một tháng: Nếu sử dụng quạt điện hàng ngày, ta tính điện năng tiêu thụ trong một tháng (30 ngày) như sau:
\[
A_{\text{tháng}} = 300 \times 30 = 9000 \text{Wh} = 9 \text{kWh}
\]
Vậy, trong một tháng, chiếc quạt điện này tiêu thụ 9 kWh điện năng. Để biết số tiền phải trả, bạn có thể nhân với đơn giá điện của công ty điện lực.
Bài Tập 7: Phân Tích Sóng Âm Trong Lý Học
Trong bài tập này, chúng ta sẽ phân tích các khía cạnh quan trọng của sóng âm trong lý học. Đặc biệt, chúng ta sẽ áp dụng kiến thức về sóng âm để hiểu rõ hơn về các hiện tượng âm thanh, tương tự như cách đội tuyển nữ Việt Nam đã chuẩn bị chiến thuật phòng ngự khi đối đầu với đội tuyển Mỹ trong kỳ World Cup 2023.
1. Định nghĩa và Đặc điểm của Sóng Âm
Sóng âm là sự lan truyền của các dao động cơ học trong môi trường vật chất như không khí, nước, hoặc chất rắn. Đặc điểm của sóng âm bao gồm:
- Tần số (\(f\))
- Bước sóng (\(\lambda\))
- Biên độ (\(A\))
- Vận tốc truyền sóng (\(v\))
2. Công Thức Liên Quan Đến Sóng Âm
Vận tốc của sóng âm trong một môi trường được tính bằng công thức:
Trong đó:
- \(v\) là vận tốc sóng (m/s)
- \(f\) là tần số sóng (Hz)
- \(\lambda\) là bước sóng (m)
3. Phân Tích Sóng Âm Trong Thực Tế
Để minh họa cho phân tích này, chúng ta có thể liên hệ đến chiến lược phòng ngự của tuyển nữ Việt Nam khi đối đầu với tuyển Mỹ. Giống như cách sóng âm có thể lan truyền và thay đổi trong các môi trường khác nhau, đội tuyển Việt Nam đã thay đổi chiến thuật phòng ngự của mình để thích ứng với sức mạnh và tốc độ của tuyển Mỹ. Các yếu tố như tần số tấn công của đối thủ (tương tự tần số sóng âm) và cách thức điều chỉnh đội hình để giảm thiểu tác động (tương tự việc điều chỉnh biên độ sóng) đã được xem xét kỹ lưỡng.
4. Ứng Dụng Sóng Âm Trong Đời Sống
Sóng âm không chỉ có vai trò quan trọng trong lý học mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực như y tế (siêu âm), công nghệ âm thanh, và truyền thông. Tương tự, việc hiểu và ứng dụng kiến thức về sóng âm có thể giúp chúng ta phát triển các chiến lược hiệu quả hơn, chẳng hạn như cách mà tuyển nữ Việt Nam đã sử dụng kiến thức và sự chuẩn bị kỹ lưỡng để tạo ra màn trình diễn ấn tượng trong trận đấu lịch sử này.

Bài Tập 8: Dạng Bài Tập Về Cân Bằng Lực
Trong vật lý, cân bằng lực là một khái niệm quan trọng khi các lực tác động lên một vật cân bằng lẫn nhau, dẫn đến trạng thái cân bằng tĩnh hoặc động. Để giải các bài tập dạng này, ta cần nắm vững các nguyên tắc cơ bản và biết cách áp dụng vào các tình huống cụ thể.
-
Khái niệm cân bằng lực:
Khi tổng hợp các lực tác động lên một vật là bằng không, vật đó đang ở trạng thái cân bằng. Nếu vật đang đứng yên, nó sẽ tiếp tục đứng yên. Nếu vật đang chuyển động, nó sẽ tiếp tục chuyển động thẳng đều.
-
Phương pháp phân tích:
Để giải bài tập về cân bằng lực, ta cần phân tích lực tác động theo từng hướng (thường là trục tọa độ Ox, Oy).
- Chia nhỏ các lực thành các thành phần theo các trục.
- Sử dụng định lý tổng hợp lực: \(\sum \vec{F} = 0\).
- Lập phương trình cân bằng cho từng trục: \(\sum F_x = 0\) và \(\sum F_y = 0\).
-
Bài tập mẫu:
Xét một vật chịu tác động của ba lực \(\vec{F_1}\), \(\vec{F_2}\) và \(\vec{F_3}\). Để vật cân bằng, ta có:
- Cân bằng theo trục Ox: \(\sum F_x = F_{1x} + F_{2x} + F_{3x} = 0\)
- Cân bằng theo trục Oy: \(\sum F_y = F_{1y} + F_{2y} + F_{3y} = 0\)
Từ đây, ta giải hệ phương trình để tìm giá trị các lực hoặc các góc mà lực tạo ra với các trục.
-
Ứng dụng thực tiễn:
Trong thực tế, bài toán cân bằng lực xuất hiện khi thiết kế cầu, nhà, và các công trình xây dựng. Việc tính toán chính xác lực tác động giúp đảm bảo sự ổn định và an toàn của các cấu trúc này.
Với việc nắm vững kiến thức về cân bằng lực, bạn sẽ dễ dàng hơn trong việc phân tích và giải quyết các bài toán phức tạp liên quan đến động lực học và tĩnh học.
Bài Tập 9: Bài Tập Về Động Lượng
Động lượng là một đại lượng vật lý quan trọng trong cơ học, được xác định bằng tích của khối lượng và vận tốc của một vật. Dưới đây là các dạng bài tập về động lượng, giúp học sinh nắm vững kiến thức về khái niệm và ứng dụng của động lượng trong thực tế.
Ví dụ 1: Bài tập động lượng cơ bản
Một quả bóng có khối lượng \(m = 0.5 \, \text{kg}\) đang di chuyển với vận tốc \(v = 10 \, \text{m/s}\). Tính động lượng của quả bóng.
Lời giải:
Động lượng \(p\) của quả bóng được tính theo công thức:
\[
p = m \times v
\]
Thay số vào ta được:
\[
p = 0.5 \, \text{kg} \times 10 \, \text{m/s} = 5 \, \text{kg} \cdot \text{m/s}
\]
Vậy động lượng của quả bóng là \(5 \, \text{kg} \cdot \text{m/s}\).
Ví dụ 2: Bài tập về bảo toàn động lượng
Hai chiếc xe có khối lượng lần lượt là \(m_1 = 1000 \, \text{kg}\) và \(m_2 = 800 \, \text{kg}\) đang di chuyển đối đầu với nhau với các vận tốc tương ứng là \(v_1 = 15 \, \text{m/s}\) và \(v_2 = -12 \, \text{m/s}\). Sau khi va chạm, hai xe dính vào nhau. Tính vận tốc chung của hai xe sau va chạm.
Lời giải:
Theo định luật bảo toàn động lượng, động lượng tổng trước và sau va chạm là như nhau:
\[
m_1 \times v_1 + m_2 \times v_2 = (m_1 + m_2) \times v
\]
Thay số vào:
\[
1000 \, \text{kg} \times 15 \, \text{m/s} + 800 \, \text{kg} \times (-12 \, \text{m/s}) = (1000 \, \text{kg} + 800 \, \text{kg}) \times v
\]
\[
15000 \, \text{kg} \cdot \text{m/s} - 9600 \, \text{kg} \cdot \text{m/s} = 1800 \, \text{kg} \times v
\]
\[
5400 \, \text{kg} \cdot \text{m/s} = 1800 \, \text{kg} \times v
\]
Do đó, vận tốc chung sau va chạm là:
\[
v = \frac{5400 \, \text{kg} \cdot \text{m/s}}{1800 \, \text{kg}} = 3 \, \text{m/s}
\]
Vậy, vận tốc chung của hai xe sau va chạm là \(3 \, \text{m/s}\).
Ví dụ 3: Bài tập về xung lượng và mối quan hệ với động lượng
Một vận động viên bóng đá sút bóng với lực \(F = 400 \, \text{N}\) trong khoảng thời gian \(t = 0.1 \, \text{s}\). Tính xung lượng của lực tác dụng lên quả bóng và động lượng của quả bóng ngay sau khi bị sút.
Lời giải:
Xung lượng \(I\) của lực được tính theo công thức:
\[
I = F \times t
\]
Thay số vào:
\[
I = 400 \, \text{N} \times 0.1 \, \text{s} = 40 \, \text{N} \cdot \text{s}
\]
Do động lượng bằng xung lượng nên động lượng của quả bóng sau khi bị sút cũng là \(40 \, \text{kg} \cdot \text{m/s}\).
Bài Tập 10: Phân Tích Đồ Thị Toán Học
Phân tích đồ thị toán học là một kỹ năng quan trọng trong việc hiểu và giải quyết các vấn đề toán học. Dưới đây là một số bài tập giúp bạn rèn luyện kỹ năng này:
-
Đồ thị của hàm số bậc hai:
Xét hàm số \( y = ax^2 + bx + c \). Vẽ đồ thị của hàm số và xác định các điểm cực trị, tọa độ đỉnh và trục đối xứng của parabol. Giải thích ý nghĩa hình học của các điểm này.
Trục đối xứng: \( x = -\frac{b}{2a} \)
Đỉnh parabol: \( y = -\frac{\Delta}{4a} \), với \( \Delta = b^2 - 4ac \)
Các điểm cực trị: Xác định bằng cách giải phương trình \( y' = 0 \)
-
Phân tích đồ thị hàm số mũ:
Xét hàm số \( y = a e^{bx} + c \). Vẽ đồ thị và tìm các điểm giao của đồ thị với trục tọa độ. Đánh giá sự thay đổi của đồ thị khi thay đổi các hệ số \( a \), \( b \), và \( c \).
Điểm giao với trục \( Ox \): Xác định \( x \) khi \( y = 0 \)
Điểm giao với trục \( Oy \): Xác định \( y \) khi \( x = 0 \)
Sự thay đổi đồ thị: Phân tích bằng cách thử nghiệm với các giá trị khác nhau của \( a \), \( b \), \( c \)
-
Đồ thị của hàm số logarit:
Xét hàm số \( y = a \log_b(x) + c \). Vẽ đồ thị và phân tích sự ảnh hưởng của các tham số \( a \), \( b \), và \( c \) đến hình dạng đồ thị.
Điểm giao với trục \( Oy \): Xác định \( y \) khi \( x = 1 \)
Đường tiệm cận: Xác định đường tiệm cận đứng của đồ thị tại \( x = 0 \)
Những bài tập trên giúp bạn nắm vững kỹ năng phân tích và vẽ đồ thị của các loại hàm số cơ bản. Việc thực hành đều đặn sẽ giúp bạn cải thiện khả năng giải quyết các bài toán liên quan đến đồ thị toán học.