Chủ đề lịch thi đấu bóng đá 1/8: Lịch thi đấu bóng đá 1/8 mang đến cho người hâm mộ những trận đấu đỉnh cao từ nhiều giải đấu quốc tế. Từ các trận chung kết căng thẳng đến những vòng loại gay cấn, hãy cùng cập nhật chi tiết từng trận đấu để không bỏ lỡ khoảnh khắc hấp dẫn của bóng đá thế giới trong ngày này.
Mục lục
- Lịch Thi Đấu Bóng Đá Ngày 1/8
- Lịch Thi Đấu Các Giải Đấu Quốc Tế Ngày 1/8
- Bài Tập Toán Có Lời Giải Hoàn Chỉnh
- Bài Tập 1: Giải Phương Trình Bậc 2
- Bài Tập 2: Tính Giá Trị Biểu Thức Đại Số
- Bài Tập 3: Giải Hệ Phương Trình Tuyến Tính
- Bài Tập 4: Phân Tích Đa Thức Thành Nhân Tử
- Bài Tập 5: Tìm Giá Trị Cực Trị Của Hàm Số
- Bài Tập 6: Tính Diện Tích Hình Tròn
- Bài Tập 7: Ứng Dụng Đạo Hàm Trong Tính Toán
- Bài Tập 8: Giải Phương Trình Mũ Và Lôgarit
- Bài Tập 9: Bài Toán Về Tỉ Lệ Thức
- Bài Tập 10: Tính Toán Số Học Cơ Bản
- Bài Tập Lý Có Lời Giải Hoàn Chỉnh
- Bài Tập 1: Định Luật Bảo Toàn Cơ Năng
- Bài Tập 2: Chuyển Động Thẳng Đều
- Bài Tập 3: Lực Hấp Dẫn Và Lực Ma Sát
- Bài Tập 4: Điện Tích Và Điện Trường
- Bài Tập 5: Tính Công Suất Điện
- Bài Tập 6: Dao Động Điều Hòa
- Bài Tập 7: Sóng Cơ Học Và Âm Thanh
- Bài Tập 8: Định Luật Vạn Vật Hấp Dẫn
- Bài Tập 9: Hiện Tượng Nhiệt Động Lực Học
- Bài Tập 10: Khúc Xạ Ánh Sáng
- Bài Tập Tiếng Anh Có Lời Giải Hoàn Chỉnh
- Bài Tập 1: Chia Động Từ Trong Các Thì
- Bài Tập 2: Cấu Trúc Câu Điều Kiện Loại 1, 2, 3
- Bài Tập 3: Tìm Lỗi Sai Trong Câu
- Bài Tập 4: Viết Lại Câu Không Đổi Nghĩa
- Bài Tập 5: Đọc Hiểu Văn Bản Tiếng Anh
- Bài Tập 6: Sử Dụng Giới Từ Chính Xác
- Bài Tập 7: Chọn Đáp Án Đúng Cho Câu Hoàn Chỉnh
- Bài Tập 8: Phân Biệt Các Thì Tiếp Diễn Và Đơn
- Bài Tập 9: Dịch Văn Bản Ngắn Sang Tiếng Anh
- Bài Tập 10: Đặt Câu Hỏi Với Từ Được Gạch Chân
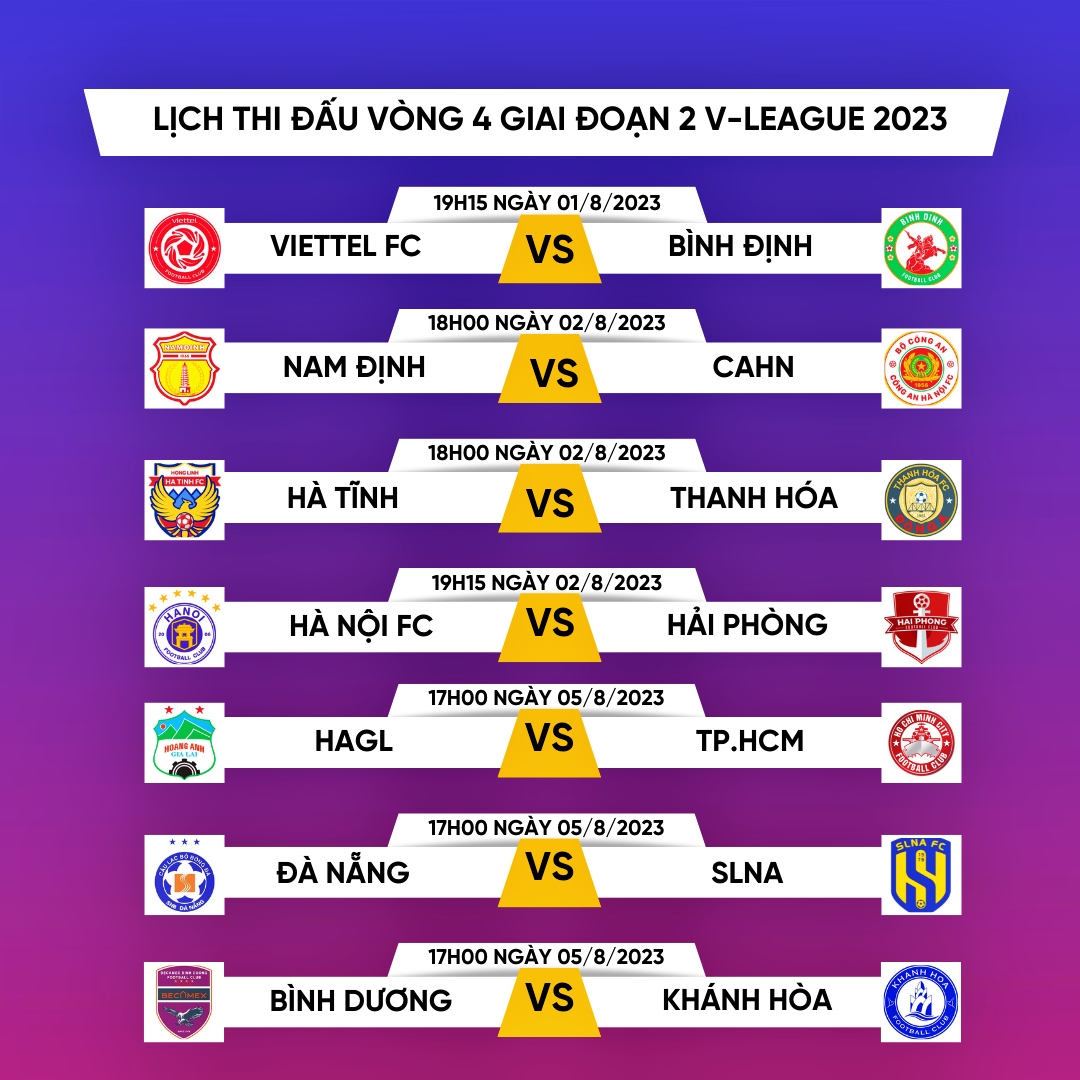
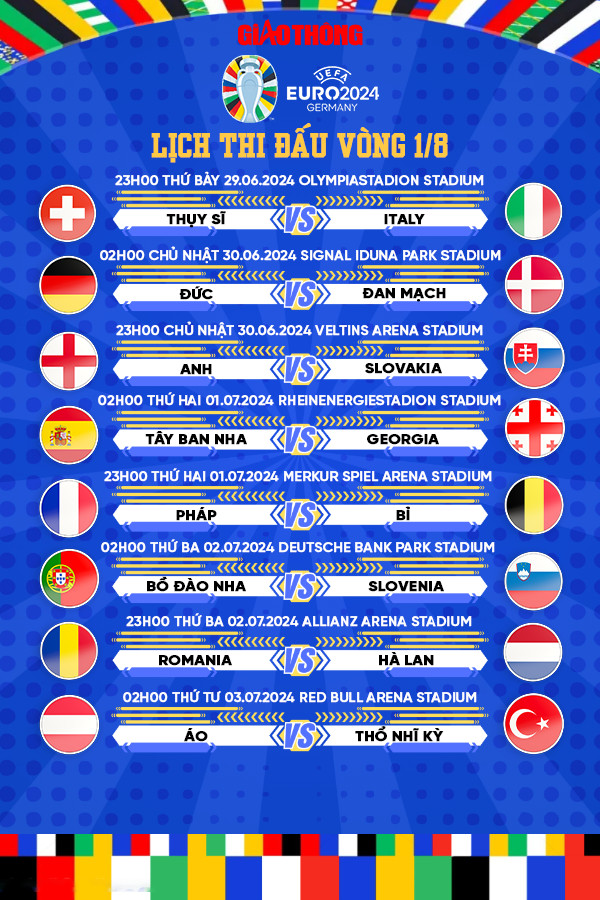
Lịch Thi Đấu Bóng Đá Ngày 1/8
Ngày 1/8 là một ngày quan trọng trong lịch thi đấu bóng đá, với nhiều trận đấu hấp dẫn diễn ra tại các giải đấu lớn trên toàn thế giới. Dưới đây là danh sách các trận đấu nổi bật trong ngày này:
1. CONCACAF Gold Cup 2021 - Chung Kết
- Thời gian: 07:30 ngày 02/08
- Trận đấu: USA vs Mexico
2. Siêu Cúp Pháp 2021
- Thời gian: 01:00 ngày 02/08
- Trận đấu: PSG vs Lille
3. Vòng 1 - Cúp Liên Đoàn Anh 2021/22
- Thời gian: 19:00 ngày 01/08
- Trận đấu: Sheffield Wed vs Huddersfield Town
4. VĐQG Thụy Điển 2021 - Vòng 13
- 20:00: Djurgardens vs Hacken
- 22:30: Kalmar vs Mjallby AIF
- 22:30: Ostersunds vs Hammarby
5. VĐQG Bỉ 2021/22 - Vòng 2
- 18:30: Union Saint Gilloise vs Club Brugge
- 21:00: Zulte Waregem vs Standard Liege
- 23:30: KAA Gent vs Beerschot VA
- 02:00: Royal Antwerp vs KV Kortrijk
6. VĐQG Áo 2021/22 - Vòng 2
- 22:00: Austria Vienna vs WSG Swarovski Tirol
- 22:00: Red Bull Salzburg vs Ried
- 22:00: Wolfsberger vs Sturm Graz
7. VĐQG Đan Mạch 2021/22 - Vòng 3
- 19:00: AGF Aarhus vs Randers
- 19:00: Silkeborg vs Aalborg
- 21:00: Vejle vs Brondby
- 23:00: Odense vs FC Copenhagen
8. VĐQG Thụy Sỹ 2021/22 - Vòng 2
- 19:15: St. Gallen vs Luzern
- 21:30: Basel vs Sion
- 21:30: Servette vs Lugano
9. VĐQG Ba Lan 2021/22 - Vòng 2
- 20:00: Warta Poznan vs Pogon Szczecin
- 22:30: Cracovia Krakow vs Slask Wroclaw
- 01:00: Jagiellonia Bialystok vs Rakow Czestochowa
10. VĐQG Romania 2021/22 - Vòng 3
- 23:30: Universitatea Craiova vs Botosani
- 02:00: UTA Arad vs Steaua Bucharest
11. Hạng 2 Đức 2021/22 - Vòng 2
- 18:30: Erzgebirge Aue vs St. Pauli
- 18:30: Hamburg vs Dynamo Dresden
Các trận đấu sẽ được phát sóng trực tiếp trên các kênh truyền hình thể thao hàng đầu. Hãy cùng đón xem và cổ vũ cho đội bóng yêu thích của bạn!
.png)
Lịch Thi Đấu Các Giải Đấu Quốc Tế Ngày 1/8
Ngày 1/8 là một ngày sôi động của bóng đá thế giới với nhiều trận đấu đáng chú ý từ các giải đấu hàng đầu. Dưới đây là lịch thi đấu chi tiết của các giải đấu quốc tế diễn ra trong ngày.
| Giải Đấu | Trận Đấu | Thời Gian (Giờ Việt Nam) |
| CONCACAF Gold Cup 2021 - Chung Kết | USA vs Mexico | 07:30 ngày 02/08 |
| Siêu Cúp Pháp 2021 | PSG vs Lille | 01:00 ngày 02/08 |
| Cúp Liên Đoàn Anh 2021/22 - Vòng 1 | Sheffield Wed vs Huddersfield Town | 19:00 ngày 01/08 |
| VĐQG Thụy Điển 2021 - Vòng 13 | Djurgardens vs Hacken | 20:00 ngày 01/08 |
| VĐQG Thụy Điển 2021 - Vòng 13 | Kalmar vs Mjallby AIF | 22:30 ngày 01/08 |
| VĐQG Thụy Điển 2021 - Vòng 13 | Ostersunds vs Hammarby | 22:30 ngày 01/08 |
| VĐQG Bỉ 2021/22 - Vòng 2 | Union Saint Gilloise vs Club Brugge | 18:30 ngày 01/08 |
| VĐQG Bỉ 2021/22 - Vòng 2 | Zulte Waregem vs Standard Liege | 21:00 ngày 01/08 |
| VĐQG Bỉ 2021/22 - Vòng 2 | KAA Gent vs Beerschot VA | 23:30 ngày 01/08 |
| VĐQG Bỉ 2021/22 - Vòng 2 | Royal Antwerp vs KV Kortrijk | 02:00 ngày 02/08 |
| VĐQG Áo 2021/22 - Vòng 2 | Austria Vienna vs WSG Swarovski Tirol | 22:00 ngày 01/08 |
| VĐQG Áo 2021/22 - Vòng 2 | Red Bull Salzburg vs Ried | 22:00 ngày 01/08 |
| VĐQG Áo 2021/22 - Vòng 2 | Wolfsberger vs Sturm Graz | 22:00 ngày 01/08 |
Hãy sắp xếp thời gian để theo dõi những trận cầu kịch tính này và không bỏ lỡ bất kỳ khoảnh khắc quan trọng nào!
Bài Tập Toán Có Lời Giải Hoàn Chỉnh
Dưới đây là một số bài tập toán có lời giải hoàn chỉnh giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán. Các bài tập được trình bày chi tiết từ cơ bản đến nâng cao, phù hợp cho học sinh và những người đam mê toán học.
-
Bài tập 1: Giải phương trình bậc hai
Giải phương trình: \[ ax^2 + bx + c = 0 \]
Lời giải:
- Tính biệt thức: \(\Delta = b^2 - 4ac\)
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
- Nếu \(\Delta = 0\), phương trình có nghiệm kép: \[ x = \frac{-b}{2a} \]
- Nếu \(\Delta < 0\), phương trình vô nghiệm.
-
Bài tập 2: Tính giá trị của biểu thức
Tính giá trị của biểu thức: \[ A = \frac{2x + 3}{x - 1} \quad \text{khi} \quad x = 5 \]
Lời giải:
- Thay \(x = 5\) vào biểu thức: \[ A = \frac{2(5) + 3}{5 - 1} = \frac{10 + 3}{4} = \frac{13}{4} = 3.25 \]
-
Bài tập 3: Giải hệ phương trình tuyến tính
Giải hệ phương trình:
\[
\begin{cases}
2x + 3y = 5 \\
x - y = 2
\end{cases}
\]Lời giải:
- Giải phương trình thứ hai: \[ x = y + 2 \]
- Thay vào phương trình thứ nhất: \[ 2(y + 2) + 3y = 5 \] \[ 2y + 4 + 3y = 5 \] \[ 5y + 4 = 5 \Rightarrow y = \frac{1}{5} \]
- Thay giá trị \(y\) vào \(x = y + 2\), ta có: \[ x = \frac{1}{5} + 2 = \frac{11}{5} \]
-
Bài tập 4: Phân tích đa thức thành nhân tử
Phân tích đa thức: \[ x^2 - 5x + 6 \]
Lời giải:
- Ta có thể phân tích thành: \[ x^2 - 5x + 6 = (x - 2)(x - 3) \]

Bài Tập 1: Giải Phương Trình Bậc 2
Giải phương trình bậc hai tổng quát có dạng:
Với các bước giải như sau:
- Bước 1: Xác định các hệ số \( a \), \( b \), \( c \) từ phương trình đã cho.
- Bước 2: Tính biệt thức \( \Delta \) theo công thức: \[ \Delta = b^2 - 4ac \]
- Bước 3: Phân loại nghiệm dựa trên giá trị của \( \Delta \):
- Nếu \( \Delta > 0 \), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
- Nếu \( \Delta = 0 \), phương trình có nghiệm kép: \[ x = \frac{-b}{2a} \]
- Nếu \( \Delta < 0 \), phương trình vô nghiệm trong tập số thực.
- Bước 4: Kết luận nghiệm của phương trình dựa trên giá trị tính toán của \( \Delta \).
Ví dụ: Giải phương trình:
- Bước 1: Xác định hệ số: \[ a = 2, \, b = -4, \, c = -6 \]
- Bước 2: Tính biệt thức: \[ \Delta = (-4)^2 - 4 \cdot 2 \cdot (-6) = 16 + 48 = 64 \]
- Bước 3: Vì \( \Delta = 64 > 0 \), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{-(-4) + \sqrt{64}}{2 \cdot 2} = \frac{4 + 8}{4} = 3 \] \[ x_2 = \frac{-(-4) - \sqrt{64}}{2 \cdot 2} = \frac{4 - 8}{4} = -1 \]
- Bước 4: Kết luận: Phương trình có hai nghiệm: \[ x_1 = 3, \quad x_2 = -1 \]

Bài Tập 2: Tính Giá Trị Biểu Thức Đại Số
Trong bài tập này, chúng ta sẽ tính giá trị của một biểu thức đại số khi biết giá trị của biến. Hãy theo dõi từng bước giải dưới đây:
Đề bài: Tính giá trị của biểu thức sau:
với \( x = 5 \).
- Bước 1: Thay giá trị \( x = 5 \) vào biểu thức \( A \).
- Biểu thức trở thành: \[ A = \frac{2(5) + 3}{5 - 1} \]
- Bước 2: Tính giá trị của tử số và mẫu số.
- Tử số: \( 2(5) + 3 = 10 + 3 = 13 \)
- Mẫu số: \( 5 - 1 = 4 \)
- Bước 3: Chia tử số cho mẫu số.
- \[ A = \frac{13}{4} = 3.25 \]
- Bước 4: Kết luận giá trị của biểu thức \( A \) khi \( x = 5 \) là: \[ A = 3.25 \]

Bài Tập 3: Giải Hệ Phương Trình Tuyến Tính
Trong bài tập này, chúng ta sẽ giải một hệ phương trình tuyến tính gồm hai phương trình hai ẩn. Các bước giải sẽ được trình bày chi tiết dưới đây.
Đề bài: Giải hệ phương trình sau:
- Bước 1: Biểu diễn một ẩn theo ẩn còn lại từ một trong hai phương trình.
- Từ phương trình thứ hai \( x - y = 2 \), ta có thể biểu diễn \( x \) theo \( y \): \[ x = y + 2 \]
- Bước 2: Thay biểu thức của \( x \) vào phương trình thứ nhất.
- Thay \( x = y + 2 \) vào phương trình thứ nhất \( 2x + 3y = 5 \), ta có: \[ 2(y + 2) + 3y = 5 \]
- Phân tích và thu gọn phương trình: \[ 2y + 4 + 3y = 5 \quad \Rightarrow \quad 5y + 4 = 5 \]
- Bước 3: Giải phương trình còn lại để tìm giá trị của \( y \).
- Trừ 4 từ cả hai vế: \[ 5y = 1 \]
- Chia cả hai vế cho 5: \[ y = \frac{1}{5} \]
- Bước 4: Thay giá trị của \( y \) vào biểu thức của \( x \).
- Thay \( y = \frac{1}{5} \) vào \( x = y + 2 \): \[ x = \frac{1}{5} + 2 = \frac{1}{5} + \frac{10}{5} = \frac{11}{5} \]
- Bước 5: Kết luận nghiệm của hệ phương trình.
- Nghiệm của hệ phương trình là: \[ x = \frac{11}{5}, \quad y = \frac{1}{5} \]
XEM THÊM:
Bài Tập 4: Phân Tích Đa Thức Thành Nhân Tử
Phân tích đa thức thành nhân tử là một kỹ năng quan trọng trong toán học, giúp đơn giản hóa các biểu thức và giải quyết các phương trình. Dưới đây là các bước phân tích một đa thức bậc hai thành nhân tử.
Bước 1: Xác định các hệ số của đa thức bậc hai dạng tổng quát:
Đa thức bậc hai có dạng tổng quát:
Trong đó:
- \(a\) là hệ số của \(x^2\)
- \(b\) là hệ số của \(x\)
- \(c\) là hằng số
Bước 2: Tìm hai số \(m\) và \(n\) sao cho:
- \(m \times n = a \times c\)
- \(m + n = b\)
Bước 3: Viết lại đa thức ban đầu bằng cách phân tích thành hai hạng tử:
Bước 4: Nhóm các hạng tử lại và đặt nhân tử chung:
Bước 5: Đặt nhân tử chung cuối cùng để hoàn thành phân tích:
Ví dụ: Phân tích đa thức \(2x^2 + 5x + 2\) thành nhân tử.
- Ở đây, \(a = 2\), \(b = 5\), và \(c = 2\).
- Tìm \(m\) và \(n\) sao cho \(m \times n = 2 \times 2 = 4\) và \(m + n = 5\). Chúng ta có \(m = 4\) và \(n = 1\).
- Viết lại đa thức: \(2x^2 + 4x + 1x + 2\).
- Nhóm lại: \((2x^2 + 4x) + (1x + 2)\).
- Đặt nhân tử chung: \(2x(x + 2) + 1(x + 2)\).
- Kết quả: \((2x + 1)(x + 2)\).
Vậy, \(2x^2 + 5x + 2\) có thể được phân tích thành nhân tử là \((2x + 1)(x + 2)\).

Bài Tập 5: Tìm Giá Trị Cực Trị Của Hàm Số
Để tìm giá trị cực trị của một hàm số, chúng ta cần thực hiện theo các bước sau:
- Cho hàm số: \( f(x) = ax^3 + bx^2 + cx + d \)
- Tính đạo hàm bậc nhất: Tính đạo hàm của hàm số \( f(x) \) để tìm hàm số đạo hàm \( f'(x) \).
\( f'(x) = 3ax^2 + 2bx + c \) - Tìm nghiệm của phương trình đạo hàm: Giải phương trình \( f'(x) = 0 \) để tìm các giá trị \( x \) làm cho đạo hàm bằng không. Những giá trị này là các điểm cực trị tiềm năng.
\( 3ax^2 + 2bx + c = 0 \) - Kiểm tra dấu của đạo hàm bậc nhất: Dùng bảng xét dấu hoặc đạo hàm bậc hai \( f''(x) \) để xác định tính chất của các điểm tìm được.
- Nếu \( f''(x) > 0 \) tại \( x = x_0 \), \( f(x) \) có cực tiểu tại điểm \( x_0 \).
- Nếu \( f''(x) < 0 \) tại \( x = x_0 \), \( f(x) \) có cực đại tại điểm \( x_0 \).
- Kết luận: Xác định các điểm cực trị và giá trị cực trị tương ứng của hàm số.
Các điểm cực trị có thể là cực đại hoặc cực tiểu, tùy thuộc vào dấu của đạo hàm bậc hai tại các điểm đó.
Ví dụ:
Xét hàm số \( f(x) = x^3 - 3x^2 + 4 \). Ta có các bước sau:
- Đạo hàm bậc nhất: \( f'(x) = 3x^2 - 6x \)
- Giải phương trình đạo hàm: \( 3x(x - 2) = 0 \) cho \( x = 0 \) hoặc \( x = 2 \)
- Đạo hàm bậc hai: \( f''(x) = 6x - 6 \). Tại \( x = 0 \), \( f''(0) = -6 < 0 \) (cực đại), và tại \( x = 2 \), \( f''(2) = 6 > 0 \) (cực tiểu).
- Kết luận: \( f(x) \) có cực đại tại \( x = 0 \) và cực tiểu tại \( x = 2 \).
Như vậy, giá trị cực đại của hàm số là \( f(0) = 4 \) và giá trị cực tiểu là \( f(2) = -4 \).

Bài Tập 6: Tính Diện Tích Hình Tròn
Trong bài tập này, chúng ta sẽ học cách tính diện tích của một hình tròn dựa trên công thức đơn giản. Hãy theo dõi các bước dưới đây để thực hiện tính toán.
- Xác định bán kính của hình tròn. Ký hiệu bán kính là \(r\).
- Áp dụng công thức tính diện tích hình tròn:
\[
S = \pi \times r^2
\]
Trong đó:
- \(S\) là diện tích hình tròn.
- \(\pi\) là hằng số Pi, thường được lấy giá trị xấp xỉ là 3.14159.
- \(r\) là bán kính của hình tròn.
- Thay thế giá trị của bán kính vào công thức và thực hiện phép nhân để tính diện tích.
- Kết quả nhận được là diện tích của hình tròn với đơn vị vuông (ví dụ: cm², m²).
Ví dụ: Nếu bán kính của hình tròn là 5 cm, diện tích của nó sẽ được tính như sau:
\[
S = 3.14159 \times 5^2 = 3.14159 \times 25 = 78.53975 \, \text{cm}^2
\]
Do đó, diện tích của hình tròn là 78.54 cm² (làm tròn đến 2 chữ số thập phân).
Bài Tập 7: Ứng Dụng Đạo Hàm Trong Tính Toán
Đạo hàm là một công cụ mạnh mẽ trong toán học, đặc biệt hữu ích trong việc giải quyết các bài toán liên quan đến tốc độ thay đổi và tối ưu hóa. Trong bài tập này, chúng ta sẽ tìm hiểu cách áp dụng đạo hàm vào các tình huống thực tế.
Giả sử bạn cần tìm cực đại hoặc cực tiểu của một hàm số, chẳng hạn như hàm f(x). Để làm điều này, bạn có thể thực hiện theo các bước sau:
- Tính đạo hàm của hàm số:
Trước tiên, bạn cần tính đạo hàm cấp một của hàm số f(x), ký hiệu là f'(x). Đạo hàm này cho biết tốc độ thay đổi của hàm số tại một điểm bất kỳ trên đường cong.
Ví dụ, nếu hàm số là f(x) = x^3 - 3x^2 + 4, thì đạo hàm của nó là:
\[ f'(x) = 3x^2 - 6x \] - Xác định các điểm dừng:
Điểm dừng là các giá trị của x tại đó f'(x) = 0. Đây là những điểm mà tốc độ thay đổi của hàm số bằng 0, thường là các điểm cực trị (cực đại hoặc cực tiểu).
Đối với ví dụ trên, giải phương trình f'(x) = 0:
\[ 3x^2 - 6x = 0 \]Kết quả cho ta các điểm dừng x = 0 và x = 2.
- Xác định cực trị:
Để xác định liệu các điểm dừng này là cực đại, cực tiểu hay điểm yên ngựa, bạn cần tính đạo hàm cấp hai f''(x):
\[ f''(x) = 6x - 6 \]Kiểm tra dấu của f''(x) tại các điểm dừng:
- Nếu f''(x) > 0, điểm đó là cực tiểu.
- Nếu f''(x) < 0, điểm đó là cực đại.
Với ví dụ trên:
- Tại x = 0, f''(0) = -6, nên đây là điểm cực đại.
- Tại x = 2, f''(2) = 6, nên đây là điểm cực tiểu.
Bằng cách áp dụng đạo hàm, chúng ta có thể dễ dàng xác định các điểm tối ưu trong nhiều bài toán khác nhau, từ việc tối ưu hóa chi phí, lợi nhuận đến việc phân tích dữ liệu thực tế.
Bài Tập 8: Giải Phương Trình Mũ Và Lôgarit
Phương trình mũ và lôgarit là một trong những chủ đề quan trọng trong toán học, ứng dụng nhiều trong các lĩnh vực khoa học, kỹ thuật và tài chính. Để giải các phương trình này, chúng ta cần nắm vững các quy tắc và công thức cơ bản liên quan đến mũ và lôgarit.
- Phương trình mũ:
Phương trình mũ có dạng tổng quát là:
\[ a^{x} = b \]Để giải phương trình này, ta lấy lôgarit cả hai vế (có thể là lôgarit tự nhiên hoặc lôgarit cơ số 10) để đưa về dạng tuyến tính:
\[ \log(a^{x}) = \log(b) \]Áp dụng tính chất lôgarit:
\[ x \cdot \log(a) = \log(b) \]Suy ra:
\[ x = \frac{\log(b)}{\log(a)} \] - Phương trình lôgarit:
Phương trình lôgarit có dạng tổng quát:
\[ \log_{a}(x) = b \]Để giải phương trình này, ta sử dụng định nghĩa của lôgarit:
\[ x = a^{b} \]Trong một số trường hợp, ta cần sử dụng các tính chất khác của lôgarit để đơn giản hóa phương trình.
- Ví dụ minh họa:
- Ví dụ 1: Giải phương trình mũ \(3^{x} = 81\).
- Ví dụ 2: Giải phương trình lôgarit \(\log_{2}(x) = 5\).
Giải: Ta có:
\[ 3^{x} = 3^{4} \]Do đó, \(x = 4\).
Giải: Sử dụng định nghĩa lôgarit, ta có:
\[ x = 2^{5} = 32 \]
Việc luyện tập giải các phương trình mũ và lôgarit sẽ giúp bạn nắm vững hơn các khái niệm và ứng dụng chúng một cách linh hoạt trong các bài toán thực tế.
Bài Tập 9: Bài Toán Về Tỉ Lệ Thức
Bài toán về tỉ lệ thức là một phần quan trọng trong toán học cơ bản, giúp chúng ta hiểu và áp dụng mối quan hệ giữa các đại lượng tỷ lệ với nhau. Bài toán tỉ lệ thường được sử dụng để giải quyết các vấn đề trong thực tế, từ tỷ lệ của bản vẽ kỹ thuật cho đến việc tính toán trong tài chính.
- Định nghĩa tỉ lệ thức:
Một tỉ lệ thức là một đẳng thức giữa hai tỷ số. Ví dụ, nếu hai tỷ số \(\frac{a}{b}\) và \(\frac{c}{d}\) bằng nhau, ta viết:
\[ \frac{a}{b} = \frac{c}{d} \]Tỉ lệ thức này được đọc là "a trên b bằng c trên d".
- Tính chất của tỉ lệ thức:
- Nếu \(\frac{a}{b} = \frac{c}{d}\), thì tích chéo của chúng là bằng nhau: \(a \cdot d = b \cdot c\).
- Nếu \(\frac{a}{b} = \frac{c}{d}\) thì ta có thể suy ra các tỉ lệ thức khác bằng cách hoán vị các đại lượng. Ví dụ: \[ \frac{a}{c} = \frac{b}{d}, \quad \frac{b}{a} = \frac{d}{c} \]
- Ứng dụng của tỉ lệ thức:
Tỉ lệ thức được sử dụng trong nhiều lĩnh vực khác nhau. Dưới đây là một số ví dụ về cách áp dụng tỉ lệ thức:
- Ví dụ 1: Một bài toán về bản đồ: Nếu trên bản đồ, khoảng cách giữa hai thành phố là 5 cm và thực tế khoảng cách là 100 km, tỉ lệ bản đồ là bao nhiêu?
- Ví dụ 2: Một công thức nấu ăn cần 2 kg đường cho 5 lít nước. Nếu muốn pha chế 8 lít nước, cần bao nhiêu kg đường?
Giải: Tỉ lệ bản đồ là:
\[ \frac{5 \text{ cm}}{100 \text{ km}} = \frac{1}{2000000} \]Tức là 1 cm trên bản đồ tương ứng với 2.000.000 cm (hay 20 km) trong thực tế.
Giải: Gọi số kg đường cần tìm là x, ta có tỉ lệ thức:
\[ \frac{2}{5} = \frac{x}{8} \]Giải ra:
\[ x = \frac{2 \times 8}{5} = 3.2 \text{ kg} \]Vậy cần 3.2 kg đường để pha chế 8 lít nước.
- Thực hành giải bài toán tỉ lệ thức:
Để nắm vững kỹ năng này, bạn nên thực hành giải các bài toán tỉ lệ thức khác nhau, từ những bài toán đơn giản đến phức tạp, và áp dụng chúng vào thực tế.
Bài Tập 10: Tính Toán Số Học Cơ Bản
Trong bài tập này, chúng ta sẽ cùng ôn lại những phép tính số học cơ bản như cộng, trừ, nhân, chia. Đây là những kỹ năng rất quan trọng, không chỉ trong học tập mà còn trong cuộc sống hàng ngày.
Hãy cùng nhau đi qua từng bước tính toán:
-
Phép Cộng
Phép cộng là phép toán cơ bản nhất. Khi cộng hai số, chúng ta sẽ nhận được tổng của chúng:
Ví dụ: \[3 + 5 = 8\]
-
Phép Trừ
Phép trừ là quá trình lấy đi một số từ một số khác:
Ví dụ: \[10 - 4 = 6\]
-
Phép Nhân
Phép nhân là cách để cộng cùng một số nhiều lần. Đây là một cách nhanh chóng để tính tổng của các nhóm giống nhau:
Ví dụ: \[4 \times 3 = 12\]
-
Phép Chia
Phép chia là quá trình chia một số thành các phần nhỏ hơn, đều nhau:
Ví dụ: \[12 \div 4 = 3\]
Các phép tính này rất quan trọng trong việc giải quyết các bài toán phức tạp hơn sau này. Hãy chắc chắn rằng bạn nắm vững các kỹ năng cơ bản này trước khi tiến đến các bài tập nâng cao hơn.
Bài Tập Lý Có Lời Giải Hoàn Chỉnh
Trong bài học này, chúng ta sẽ cùng nhau đi qua các bài tập lý thuyết có lời giải chi tiết. Mỗi bài tập sẽ được giải thích tường tận từng bước, giúp bạn hiểu rõ hơn về các khái niệm và cách áp dụng chúng trong các tình huống thực tế. Hãy theo dõi kỹ lưỡng và làm theo từng bước để đạt được kết quả tốt nhất.
- Bài 1: Tính vận tốc của một vật rơi tự do sau 5 giây.
- Bước 1: Xác định công thức cần sử dụng: \[v = g \times t\]
- Bước 2: Thay giá trị vào công thức: \[v = 9.8 \times 5 = 49 \, \text{m/s}\]
- Bước 3: Kết luận: Vận tốc của vật sau 5 giây là 49 m/s.
- Bài 2: Tính công suất của một máy phát điện biết rằng nó phát ra một lượng điện năng là 5000 J trong thời gian 10 giây.
- Bước 1: Sử dụng công thức công suất: \[P = \frac{W}{t}\]
- Bước 2: Thay số vào công thức: \[P = \frac{5000}{10} = 500 \, \text{W}\]
- Bước 3: Kết luận: Công suất của máy phát điện là 500 W.
- Bài 3: Xác định lực căng của dây khi một vật nặng 10 kg được treo đứng yên.
- Bước 1: Xác định lực tác dụng: Lực căng dây chính là trọng lực tác dụng lên vật.
- Bước 2: Áp dụng công thức: \[F = m \times g\]
- Bước 3: Thay số: \[F = 10 \times 9.8 = 98 \, \text{N}\]
- Bước 4: Kết luận: Lực căng của dây là 98 N.
Giải:
Giải:
Giải:
Các bài tập trên giúp củng cố kiến thức lý thuyết và thực hành các công thức vật lý cơ bản. Hãy tiếp tục luyện tập để thành thạo hơn trong việc giải các bài toán vật lý.
Bài Tập 1: Định Luật Bảo Toàn Cơ Năng
Định luật bảo toàn cơ năng là một trong những định luật cơ bản trong vật lý, đặc biệt quan trọng trong việc nghiên cứu các hiện tượng động học. Định luật này khẳng định rằng, trong một hệ kín (không có lực ngoại lai tác động), tổng cơ năng của hệ luôn được bảo toàn.
Để hiểu rõ hơn về định luật này, chúng ta cùng xem xét một bài toán mẫu dưới đây:
Bài toán
Một vật có khối lượng m được thả rơi tự do từ độ cao h so với mặt đất. Bỏ qua lực cản của không khí, hãy tính:
- Vận tốc của vật khi chạm đất.
- Cơ năng của vật tại vị trí cao nhất và tại thời điểm ngay trước khi chạm đất.
Giải
1. Vận tốc của vật khi chạm đất
Theo định luật bảo toàn cơ năng, ta có:
\[ E_{\text{ban đầu}} = E_{\text{tại mặt đất}} \]
Tại vị trí cao nhất, vật chỉ có thế năng:
\[ E_{\text{ban đầu}} = W = mgh \]
Khi vật chạm đất, toàn bộ thế năng đã chuyển thành động năng:
\[ E_{\text{tại mặt đất}} = K = \frac{1}{2} mv^2 \]
Theo định luật bảo toàn cơ năng, ta có:
\[ mgh = \frac{1}{2} mv^2 \]
Suy ra:
\[ v = \sqrt{2gh} \]
2. Cơ năng của vật tại các vị trí
Tại vị trí cao nhất:
- Thế năng: \[ W = mgh \]
- Động năng: \[ K = 0 \]
- Cơ năng tổng: \[ E = mgh \]
Tại thời điểm ngay trước khi chạm đất:
- Thế năng: \[ W = 0 \]
- Động năng: \[ K = \frac{1}{2} mv^2 = mgh \]
- Cơ năng tổng: \[ E = mgh \]
Như vậy, qua bài toán này, chúng ta thấy rằng tổng cơ năng của vật luôn được bảo toàn trong suốt quá trình rơi, khẳng định đúng đắn của định luật bảo toàn cơ năng.
Bài Tập 2: Chuyển Động Thẳng Đều
Trong bài tập này, chúng ta sẽ tìm hiểu về chuyển động thẳng đều, một trong những dạng chuyển động cơ bản nhất trong vật lý. Chuyển động thẳng đều là chuyển động có quỹ đạo là một đường thẳng và tốc độ của vật không đổi theo thời gian.
Chúng ta có thể biểu diễn chuyển động thẳng đều thông qua các công thức sau:
- Phương trình chuyển động: \[ x = x_0 + vt \]
Trong đó:
- \( x \) là vị trí của vật tại thời điểm \( t \).
- \( x_0 \) là vị trí ban đầu của vật.
- \( v \) là vận tốc không đổi của vật.
- \( t \) là thời gian chuyển động.
- Công thức tính quãng đường: \[ s = v \times t \]
Trong đó:
- \( s \) là quãng đường vật đi được.
- \( v \) là vận tốc của vật.
- \( t \) là thời gian vật chuyển động.
Ví dụ: Một chiếc xe di chuyển với vận tốc không đổi 60 km/h. Hãy tính quãng đường mà xe đi được sau 2 giờ.
- Bước 1: Xác định các giá trị đã biết: \( v = 60 \) km/h, \( t = 2 \) giờ.
- Bước 2: Áp dụng công thức tính quãng đường: \[ s = v \times t = 60 \times 2 = 120 \text{ km} \]
- Bước 3: Kết luận: Xe đi được 120 km sau 2 giờ.
Thông qua ví dụ trên, chúng ta có thể thấy được sự đơn giản nhưng hữu ích của việc áp dụng các công thức cơ bản trong việc giải quyết các bài toán liên quan đến chuyển động thẳng đều. Bài tập này không chỉ giúp các bạn củng cố kiến thức lý thuyết mà còn rèn luyện kỹ năng giải bài tập một cách logic và chính xác.
Bài Tập 3: Lực Hấp Dẫn Và Lực Ma Sát
Trong bài tập này, chúng ta sẽ nghiên cứu về lực hấp dẫn và lực ma sát. Đây là hai lực rất quan trọng trong các bài toán cơ học, giúp chúng ta hiểu rõ hơn về cách các vật thể tương tác trong tự nhiên.
1. Lực Hấp Dẫn
Lực hấp dẫn là lực hút giữa hai vật thể có khối lượng. Định luật vạn vật hấp dẫn của Newton cho biết lực hấp dẫn giữa hai vật được tính bằng công thức:
\[
F = G \frac{m_1 \cdot m_2}{r^2}
\]
Trong đó:
- \(F\) là lực hấp dẫn (N)
- \(G\) là hằng số hấp dẫn \(\approx 6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\)
- \(m_1\) và \(m_2\) là khối lượng của hai vật (kg)
- \(r\) là khoảng cách giữa hai vật (m)
Ví dụ: Tính lực hấp dẫn giữa Trái Đất (có khối lượng \(\approx 5.97 \times 10^{24}\, \text{kg}\)) và Mặt Trăng (có khối lượng \(\approx 7.35 \times 10^{22}\, \text{kg}\)), khi khoảng cách giữa chúng là \(3.84 \times 10^8 \, \text{m}\).
Áp dụng công thức ta có:
\[
F = 6.674 \times 10^{-11} \cdot \frac{5.97 \times 10^{24} \cdot 7.35 \times 10^{22}}{(3.84 \times 10^8)^2} \approx 1.98 \times 10^{20} \, \text{N}
\]
2. Lực Ma Sát
Lực ma sát là lực cản trở chuyển động tương đối giữa hai bề mặt tiếp xúc. Lực ma sát được chia thành ba loại chính: ma sát trượt, ma sát lăn và ma sát nghỉ.
Lực ma sát trượt được tính bằng công thức:
\[
F_{\text{ms}} = \mu \cdot N
\]
Trong đó:
- \(F_{\text{ms}}\) là lực ma sát (N)
- \(\mu\) là hệ số ma sát
- \(N\) là lực pháp tuyến (N)
Ví dụ: Tính lực ma sát trượt khi một vật có khối lượng 10 kg trượt trên mặt phẳng với hệ số ma sát \(\mu = 0.3\).
Áp dụng công thức ta có:
\[
N = m \cdot g = 10 \cdot 9.8 = 98 \, \text{N}
\]
\[
F_{\text{ms}} = 0.3 \cdot 98 = 29.4 \, \text{N}
\]
Qua ví dụ này, chúng ta có thể thấy được cách áp dụng các công thức của lực hấp dẫn và lực ma sát vào các bài toán thực tiễn.
Bài Tập 4: Điện Tích Và Điện Trường
Bài tập này sẽ giúp bạn củng cố kiến thức về điện tích và điện trường. Chúng ta sẽ đi qua các khái niệm cơ bản, định lý và cách áp dụng chúng trong các bài toán thực tế. Hãy làm theo các bước dưới đây:
-
Điện tích:
Điện tích là một tính chất vật lý của vật chất mà qua đó vật thể có thể tương tác với lực điện. Đơn vị đo điện tích là Coulomb (C). Có hai loại điện tích: điện tích dương (+) và điện tích âm (-).
- Điện tích cùng dấu thì đẩy nhau.
- Điện tích trái dấu thì hút nhau.
-
Định luật Coulomb:
Định luật Coulomb mô tả lực tương tác giữa hai điện tích điểm:
\[
F = k_e \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]Trong đó:
- \( F \): Lực tương tác giữa hai điện tích (N).
- \( k_e \): Hằng số điện môi (\( 8.99 \times 10^9 \, Nm^2/C^2 \)).
- \( q_1, q_2 \): Độ lớn của hai điện tích (C).
- \( r \): Khoảng cách giữa hai điện tích (m).
-
Điện trường:
Điện trường là vùng không gian xung quanh một điện tích, nơi mà lực điện có thể tác động lên các điện tích khác. Cường độ điện trường tại một điểm được xác định bởi công thức:
\[
E = k_e \cdot \frac{|Q|}{r^2}
\]Trong đó:
- \( E \): Cường độ điện trường tại điểm đó (V/m).
- \( Q \): Điện tích tạo ra điện trường (C).
- \( r \): Khoảng cách từ điện tích đến điểm đó (m).
-
Bài tập áp dụng:
- Tính lực tương tác giữa hai điện tích \( q_1 = 5 \, \mu C \) và \( q_2 = -3 \, \mu C \) cách nhau 2 cm.
- Xác định cường độ điện trường tại một điểm cách điện tích \( Q = 4 \, \mu C \) một khoảng 3 cm.
Hãy áp dụng các công thức trên để giải quyết các bài toán này. Sau khi tính toán, so sánh kết quả với các giá trị thực tế để hiểu rõ hơn về tác động của điện tích và điện trường.
Chúc bạn học tốt và thành công trong việc nắm vững kiến thức về điện tích và điện trường!
Bài Tập 5: Tính Công Suất Điện
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính công suất điện dựa trên các công thức cơ bản và áp dụng chúng vào các bài toán cụ thể. Công suất điện là một trong những đại lượng quan trọng trong việc đo lường hiệu suất của các thiết bị điện.
1. Công thức tính công suất điện
Công suất điện \(P\) được tính bằng tích của hiệu điện thế \(U\) và cường độ dòng điện \(I\), hay:
Trong đó:
- \(P\) là công suất điện (đơn vị: Watt - W).
- \(U\) là hiệu điện thế (đơn vị: Volt - V).
- \(I\) là cường độ dòng điện (đơn vị: Ampere - A).
2. Tính công suất trong mạch điện trở
Khi mạch điện chứa các điện trở, công suất còn có thể tính bằng công thức:
Trong đó \(R\) là điện trở của mạch (đơn vị: Ohm - Ω).
3. Bài tập áp dụng
- Tính công suất tiêu thụ của một thiết bị điện có điện trở \(10 \, \Omega\) khi nó được mắc vào hiệu điện thế \(220 \, V\).
- Một bóng đèn sử dụng dòng điện \(0.5 \, A\) và được mắc vào nguồn điện \(12 \, V\). Hãy tính công suất của bóng đèn.
Để giải các bài tập trên, hãy áp dụng các công thức đã học và thay các giá trị vào để tính toán.
4. Kết luận
Việc nắm vững cách tính công suất điện giúp chúng ta đánh giá hiệu quả hoạt động của các thiết bị điện trong thực tế, từ đó sử dụng chúng một cách hợp lý và tiết kiệm năng lượng.

Bài Tập 6: Dao Động Điều Hòa
Dao động điều hòa là một trong những khái niệm quan trọng trong Vật lý, đặc biệt là trong cơ học. Đây là một dạng chuyển động mà vật di chuyển qua lại quanh một vị trí cân bằng cố định với chu kỳ không đổi. Để hiểu rõ hơn về dao động điều hòa, chúng ta sẽ cùng giải quyết bài tập dưới đây.
- Khảo sát dao động điều hòa:
Giả sử một vật có khối lượng \(m\) gắn vào lò xo với độ cứng \(k\) và đang dao động điều hòa. Hãy xác định phương trình chuyển động của vật.
Giải:
Phương trình dao động điều hòa có dạng:
\[
x(t) = A \cos(\omega t + \varphi)
\]Trong đó:
- \(x(t)\): Li độ của vật tại thời điểm \(t\).
- \(A\): Biên độ dao động, là giá trị lớn nhất của li độ.
- \(\omega\): Tần số góc, được xác định bằng công thức \(\omega = \sqrt{\frac{k}{m}}\).
- \(\varphi\): Pha ban đầu, xác định trạng thái dao động tại thời điểm \(t = 0\).
- Tính năng lượng trong dao động điều hòa:
Năng lượng toàn phần của hệ dao động điều hòa không đổi theo thời gian và bao gồm động năng và thế năng.
\[
W = W_{\text{động}} + W_{\text{thế}} = \frac{1}{2}kA^2
\]Trong đó:
- \(W_{\text{động}} = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2A^2 \sin^2(\omega t + \varphi)\)
- \(W_{\text{thế}} = \frac{1}{2}kx^2 = \frac{1}{2}kA^2 \cos^2(\omega t + \varphi)\)
- Chu kỳ và tần số của dao động điều hòa:
Chu kỳ \(T\) là thời gian để vật thực hiện một dao động toàn phần, và tần số \(f\) là số dao động thực hiện được trong một đơn vị thời gian:
\[
T = \frac{2\pi}{\omega}, \quad f = \frac{1}{T} = \frac{\omega}{2\pi}
\]Với \(\omega = \sqrt{\frac{k}{m}}\), ta có thể viết lại:
\[
T = 2\pi \sqrt{\frac{m}{k}}, \quad f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]
Với những bài tập trên, bạn đã có một cái nhìn tổng quan về dao động điều hòa và cách tính toán các đại lượng liên quan. Hãy áp dụng những kiến thức này vào các bài tập thực tế để hiểu rõ hơn về hiện tượng vật lý này.
Bài Tập 7: Sóng Cơ Học Và Âm Thanh
Trong bài học này, chúng ta sẽ tìm hiểu về sóng cơ học và âm thanh, bao gồm các khái niệm cơ bản và bài tập ứng dụng để hiểu rõ hơn về chúng.
I. Khái niệm cơ bản về sóng cơ học
Sóng cơ học là quá trình lan truyền của dao động cơ trong môi trường vật chất. Các sóng này cần môi trường để lan truyền, và có thể là sóng ngang hoặc sóng dọc, phụ thuộc vào hướng dao động so với hướng lan truyền của sóng.
1. Sóng ngang
Sóng ngang là loại sóng mà các phần tử của môi trường dao động vuông góc với phương truyền sóng. Ví dụ: sóng trên mặt nước.
2. Sóng dọc
Sóng dọc là loại sóng mà các phần tử của môi trường dao động theo phương song song với phương truyền sóng. Ví dụ: sóng âm trong không khí.
II. Khái niệm về âm thanh
Âm thanh là một dạng sóng cơ học lan truyền trong môi trường khí, lỏng, hoặc rắn. Các đặc điểm chính của âm thanh bao gồm:
- Biên độ (A): Biên độ càng lớn thì âm càng to.
- Tần số (f): Tần số càng cao thì âm càng cao.
- Vận tốc truyền âm (v): Phụ thuộc vào môi trường, với tốc độ lớn nhất trong chất rắn, sau đó là chất lỏng và nhỏ nhất trong chất khí.
III. Bài tập ứng dụng
Hãy cùng giải quyết một số bài tập liên quan đến sóng cơ học và âm thanh để củng cố kiến thức:
- Cho một sợi dây căng với tần số dao động \(f = 50\text{ Hz}\) và bước sóng \(\lambda = 2\text{ m}\). Tính vận tốc truyền sóng trên dây.
- Một âm thanh có tần số \(f = 440\text{ Hz}\) được phát ra trong không khí, biết vận tốc truyền âm trong không khí là \(v = 343\text{ m/s}\). Tính bước sóng của âm thanh này.
Hướng dẫn giải:
- Đối với bài 1, sử dụng công thức tính vận tốc sóng: \( v = f \times \lambda \).
- Đối với bài 2, cũng sử dụng công thức tính vận tốc sóng để tìm bước sóng: \( \lambda = \frac{v}{f} \).
Kết quả bài tập sẽ giúp bạn hiểu rõ hơn về mối quan hệ giữa tần số, bước sóng và vận tốc truyền sóng trong các môi trường khác nhau.
Bài Tập 8: Định Luật Vạn Vật Hấp Dẫn
Trong bài học này, chúng ta sẽ tìm hiểu về Định luật Vạn vật hấp dẫn, được phát hiện bởi Isaac Newton. Định luật này đóng vai trò quan trọng trong việc giải thích cách các vật thể trong vũ trụ tương tác với nhau thông qua lực hấp dẫn.
1. Khái niệm về Lực Hấp Dẫn
Lực hấp dẫn là lực tương tác giữa hai vật thể có khối lượng. Định luật này được phát biểu như sau:
“Mọi vật thể trong vũ trụ đều hút nhau bằng một lực có cường độ tỷ lệ thuận với tích của khối lượng của chúng và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.”
2. Công thức của Định Luật Vạn Vật Hấp Dẫn
Định luật này có thể biểu diễn bằng công thức:
\[
F = G \cdot \frac{m_1 \cdot m_2}{r^2}
\]
- Ở đây \( F \) là lực hấp dẫn giữa hai vật.
- \( G \) là hằng số hấp dẫn có giá trị \(6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\).
- \( m_1 \) và \( m_2 \) là khối lượng của hai vật.
- \( r \) là khoảng cách giữa tâm của hai vật.
3. Ứng dụng của Định Luật Vạn Vật Hấp Dẫn
Định luật này có nhiều ứng dụng quan trọng trong đời sống và khoa học:
- Giải thích quỹ đạo của hành tinh: Định luật này giúp giải thích tại sao các hành tinh di chuyển theo quỹ đạo quanh Mặt Trời.
- Hướng dẫn thiết kế tàu vũ trụ: Khi thiết kế đường bay cho tàu vũ trụ, các nhà khoa học dựa vào định luật này để xác định lực cần thiết để tàu có thể thoát khỏi lực hút của Trái Đất.
- Dự báo hiện tượng thiên văn: Định luật này được sử dụng để dự đoán các hiện tượng như nhật thực, nguyệt thực, và quỹ đạo của các sao chổi.
4. Bài Tập Thực Hành
Dưới đây là một số bài tập để bạn luyện tập áp dụng định luật Vạn vật hấp dẫn:
- Tính lực hấp dẫn giữa hai vật có khối lượng lần lượt là 5kg và 10kg, đặt cách nhau 2 mét.
- Tính lực hấp dẫn mà Trái Đất tác dụng lên Mặt Trăng. Cho rằng khối lượng Trái Đất là \(5.972 \times 10^{24} \, \text{kg}\), khối lượng Mặt Trăng là \(7.348 \times 10^{22} \, \text{kg}\), và khoảng cách giữa Trái Đất và Mặt Trăng là \(3.844 \times 10^8 \, \text{m}\).
Qua những bài tập này, bạn sẽ hiểu rõ hơn về cách áp dụng định luật Vạn vật hấp dẫn vào các tình huống thực tế.

Bài Tập 9: Hiện Tượng Nhiệt Động Lực Học
Nhiệt động lực học là một lĩnh vực nghiên cứu về mối quan hệ giữa nhiệt, công, và năng lượng trong các hệ thống vật lý. Các hiện tượng nhiệt động lực học có thể được áp dụng để giải thích nhiều quá trình tự nhiên và công nghiệp, từ sự giãn nở của khí đến hiệu suất của động cơ nhiệt.
Dưới đây là các bài tập giúp bạn nắm vững kiến thức về hiện tượng nhiệt động lực học:
-
Quá trình đẳng nhiệt:
Giả sử một khí lý tưởng thực hiện một quá trình đẳng nhiệt từ trạng thái ban đầu có áp suất \[ P_1 \] và thể tích \[ V_1 \] đến trạng thái có áp suất \[ P_2 \] và thể tích \[ V_2 \]. Hãy tính công mà khí thực hiện trong quá trình này.
Áp dụng công thức: \[ W = nRT \ln \left(\frac{V_2}{V_1}\right) = nRT \ln \left(\frac{P_1}{P_2}\right) \]
-
Định luật thứ nhất của nhiệt động lực học:
Một hệ thống nhận nhiệt lượng \[ Q \] và sinh công \[ W \]. Hãy xác định sự thay đổi nội năng \[ \Delta U \] của hệ thống.
Áp dụng công thức: \[ \Delta U = Q - W \]
-
Hiệu suất của động cơ Carnot:
Một động cơ Carnot hoạt động giữa hai nguồn nhiệt có nhiệt độ \[ T_1 \] và \[ T_2 \] với \[ T_1 > T_2 \]. Hãy tính hiệu suất \[ \eta \] của động cơ này.
Áp dụng công thức: \[ \eta = 1 - \frac{T_2}{T_1} \]
-
Quá trình đẳng áp:
Trong một quá trình đẳng áp, một lượng khí lý tưởng thực hiện công \[ W \] khi thể tích thay đổi từ \[ V_1 \] đến \[ V_2 \]. Hãy tính nhiệt lượng \[ Q \] mà hệ thống nhận được.
Áp dụng công thức: \[ Q = \Delta U + W \]
-
Chu trình nhiệt động:
Hãy mô tả chu trình nhiệt động của một động cơ nhiệt lý tưởng, nêu rõ các quá trình nhiệt động cơ bản (đẳng nhiệt, đẳng áp, đẳng tích, và đoạn nhiệt) và cách chúng ảnh hưởng đến sự truyền năng lượng trong hệ thống.
Hy vọng rằng những bài tập trên sẽ giúp bạn hiểu rõ hơn về hiện tượng nhiệt động lực học và các ứng dụng của nó trong thực tế.
Bài Tập 10: Khúc Xạ Ánh Sáng
Khúc xạ ánh sáng là hiện tượng ánh sáng bị thay đổi hướng khi truyền qua ranh giới giữa hai môi trường có chiết suất khác nhau. Để hiểu rõ hơn về hiện tượng này, chúng ta sẽ cùng thực hiện các bài tập sau.
-
Một tia sáng truyền từ không khí vào nước với góc tới \(\theta_1 = 30^\circ\). Biết chiết suất của nước là \(n_2 = 1,33\), hãy tính góc khúc xạ \(\theta_2\).
Lời giải:
Sử dụng định luật Snell:
\[ n_1 \sin(\theta_1) = n_2 \sin(\theta_2) \]Với chiết suất của không khí \(n_1 \approx 1\), ta có:
\[ \sin(\theta_2) = \frac{n_1 \sin(\theta_1)}{n_2} = \frac{\sin(30^\circ)}{1,33} \approx 0,3759 \]Suy ra góc khúc xạ:
\[ \theta_2 \approx \arcsin(0,3759) \approx 22^\circ \] -
Một tia sáng chiếu từ thủy tinh (chiết suất \(n = 1,5\)) ra ngoài không khí với góc tới \(\theta_1 = 45^\circ\). Tính góc khúc xạ \(\theta_2\) khi ánh sáng ra khỏi môi trường thủy tinh.
Lời giải:
Áp dụng định luật Snell như sau:
\[ n_1 \sin(\theta_1) = n_2 \sin(\theta_2) \]Với \(n_1 = 1,5\) và \(n_2 \approx 1\), ta có:
\[ \sin(\theta_2) = \frac{1,5 \cdot \sin(45^\circ)}{1} \approx 1,06 \]Do giá trị này lớn hơn 1, tia sáng không bị khúc xạ mà phản xạ toàn phần.
-
Một tia sáng chiếu xiên vào mặt nước dưới góc tới \(\theta_1\). Chiết suất của không khí là \(n_1 = 1\) và của nước là \(n_2 = 1,33\). Xác định góc tới giới hạn \(\theta_{gh}\) để xảy ra hiện tượng phản xạ toàn phần.
Lời giải:
Góc tới giới hạn khi khúc xạ ra không khí là:
\[ \sin(\theta_{gh}) = \frac{n_2}{n_1} = \frac{1}{1,33} \approx 0,75 \] \p>Suy ra: \[ \theta_{gh} \approx \arcsin(0,75) \approx 48,6^\circ \]
Bài Tập Tiếng Anh Có Lời Giải Hoàn Chỉnh
Trong bài tập này, chúng ta sẽ đi sâu vào các dạng bài tập tiếng Anh phổ biến, giúp bạn nắm vững ngữ pháp và từ vựng cơ bản, cũng như cải thiện kỹ năng nghe, nói, đọc và viết.
Bài tập 1: Chia động từ trong ngoặc
Yêu cầu: Chia động từ trong ngoặc cho đúng thì.
- He (go) to school every day.
- They (not/like) playing soccer.
- She (study) for her exams now.
Hướng dẫn giải:
- He (goes) to school every day.
- They (do not like) playing soccer.
- She (is studying) for her exams now.
Bài tập 2: Viết lại câu
Yêu cầu: Viết lại câu sau cho cùng nghĩa nhưng sử dụng cấu trúc khác.
- She is too young to drive a car.
- They have never been to New York.
- Tom is taller than Jerry.
Hướng dẫn giải:
- She is not old enough to drive a car.
- This is the first time they have been to New York.
- Jerry is shorter than Tom.
Bài tập 3: Nghe và điền từ còn thiếu
Yêu cầu: Nghe đoạn hội thoại và điền từ còn thiếu vào chỗ trống.
- He ______ (1) a student at XYZ University.
- They are ______ (2) soccer in the park.
- She ______ (3) to the store every Saturday.
Hướng dẫn giải:
- (1) is
- (2) playing
- (3) goes
Với các bài tập trên, bạn sẽ củng cố được nền tảng ngữ pháp và từ vựng, đồng thời nâng cao khả năng sử dụng tiếng Anh một cách linh hoạt trong nhiều tình huống khác nhau. Đừng quên luyện tập thường xuyên để đạt kết quả tốt nhất!

Bài Tập 1: Chia Động Từ Trong Các Thì
Chia động từ trong các thì là một kỹ năng quan trọng trong tiếng Anh. Để giúp bạn nắm vững kiến thức này, dưới đây là một bài tập thực hành chi tiết với các bước hướng dẫn cụ thể.
-
Chọn thì phù hợp: Để chia động từ đúng, trước hết bạn cần xác định thì của câu dựa trên ngữ cảnh hoặc dấu hiệu thời gian. Dưới đây là một số thì cơ bản:
- Hiện tại đơn: She walks to school every day.
- Quá khứ đơn: They watched a movie last night.
- Tương lai đơn: We will visit the museum tomorrow.
- Hiện tại hoàn thành: I have lived here for 5 years.
- Quá khứ hoàn thành: By the time he arrived, they had left.
-
Xác định chủ ngữ và động từ: Sau khi xác định được thì, bạn cần chú ý đến chủ ngữ và động từ trong câu. Chia động từ dựa trên thì đã chọn và dạng của chủ ngữ (số ít hoặc số nhiều).
- Nếu chủ ngữ là số ít (he, she, it), động từ thường thêm "s" hoặc "es" trong thì hiện tại đơn: He plays football.
- Nếu chủ ngữ là số nhiều (we, they), động từ không thay đổi trong thì hiện tại đơn: They play football.
-
Chia động từ: Dưới đây là ví dụ chi tiết cho từng thì:
Thì Động từ (Nguyên mẫu: to eat) Ví dụ Hiện tại đơn eats She eats an apple every morning. Quá khứ đơn ate He ate dinner at 7 PM. Tương lai đơn will eat They will eat out tomorrow. Hiện tại hoàn thành have/has eaten I have eaten sushi before. Quá khứ hoàn thành had eaten She had eaten breakfast before going to work. -
Thực hành: Để củng cố kiến thức, bạn hãy tự chia động từ trong các câu sau đây:
- Mary (to go) ________ to the gym every day.
- We (to see) ________ that movie last week.
- They (to travel) ________ to Japan next year.
- I (to read) ________ this book three times.
- She (to finish) ________ her work before the deadline.
Hãy thử hoàn thành các câu trên và kiểm tra lại với bảng chia động từ ở bước 3.
Bài Tập 2: Cấu Trúc Câu Điều Kiện Loại 1, 2, 3
Câu điều kiện là một cấu trúc ngữ pháp quan trọng trong Tiếng Anh, thường được sử dụng để diễn tả một giả thuyết và kết quả của nó. Câu điều kiện gồm ba loại chính: Loại 1, Loại 2, và Loại 3. Mỗi loại có cấu trúc và cách sử dụng khác nhau.
Cấu Trúc Câu Điều Kiện Loại 1
Câu điều kiện loại 1 được sử dụng để diễn tả một sự việc có khả năng xảy ra trong tương lai.
- Cấu trúc: If + S + V (hiện tại đơn), S + will + V (nguyên mẫu)
- Ví dụ:
- If it rains, we will stay at home. (Nếu trời mưa, chúng ta sẽ ở nhà.)
- If she studies hard, she will pass the exam. (Nếu cô ấy học chăm chỉ, cô ấy sẽ vượt qua kỳ thi.)
Cấu Trúc Câu Điều Kiện Loại 2
Câu điều kiện loại 2 dùng để diễn tả một sự việc không có thật hoặc ít có khả năng xảy ra ở hiện tại hoặc tương lai.
- Cấu trúc: If + S + V (quá khứ đơn), S + would + V (nguyên mẫu)
- Ví dụ:
- If I were you, I would go to the party. (Nếu tôi là bạn, tôi sẽ đi dự tiệc.)
- If he had more time, he would travel the world. (Nếu anh ấy có nhiều thời gian hơn, anh ấy sẽ du lịch vòng quanh thế giới.)
Cấu Trúc Câu Điều Kiện Loại 3
Câu điều kiện loại 3 được sử dụng để diễn tả một sự việc không có thật trong quá khứ, thường mang ý nghĩa tiếc nuối.
- Cấu trúc: If + S + had + V (quá khứ phân từ), S + would have + V (quá khứ phân từ)
- Ví dụ:
- If they had known the truth, they would have acted differently. (Nếu họ đã biết sự thật, họ đã hành động khác đi.)
- If she had studied harder, she would have passed the exam. (Nếu cô ấy đã học chăm chỉ hơn, cô ấy đã vượt qua kỳ thi.)
Bài Tập Thực Hành
- Viết lại câu sau đây sử dụng cấu trúc câu điều kiện loại 1:
If it (rain), we (stay) at home.
- Viết lại câu sau đây sử dụng cấu trúc câu điều kiện loại 2:
If I (be) you, I (go) to the party.
- Viết lại câu sau đây sử dụng cấu trúc câu điều kiện loại 3:
If they (know) the truth, they (act) differently.
Bài Tập 3: Tìm Lỗi Sai Trong Câu
Trong bài tập này, các em hãy đọc kỹ các câu dưới đây và tìm ra lỗi sai về ngữ pháp, chính tả hoặc cú pháp. Để hoàn thành bài tập, các em cần xem xét các yếu tố như sự hợp lý trong cấu trúc câu, cách dùng từ ngữ và mối quan hệ giữa các thành phần trong câu.
-
Câu: "Lịch thi đấu bóng đá hôm nay 1/8 bao gồm các trận của V.League, Ngoại hạng Anh và Ligue 1."
-
Lỗi sai: Câu này có thể gây hiểu nhầm vì lịch thi đấu ngày 1/8 có nhiều giải đấu khác nhau, không chỉ là V.League, Ngoại hạng Anh và Ligue 1. Điều này khiến thông tin trở nên không chính xác.
-
Sửa lại: "Lịch thi đấu bóng đá hôm nay 1/8 bao gồm các trận từ nhiều giải đấu lớn như V.League, Ngoại hạng Anh, Ligue 1, cùng nhiều giải đấu quốc tế khác."
-
-
Câu: "Trận đấu giữa Sheffield Wed và Huddersfield Town diễn ra vào lúc 19:00 ngày 1/8 thuộc giải đấu Siêu Cúp Pháp."
-
Lỗi sai: Trận đấu này thực tế không thuộc Siêu Cúp Pháp mà thuộc Cúp Liên Đoàn Anh.
-
Sửa lại: "Trận đấu giữa Sheffield Wed và Huddersfield Town diễn ra vào lúc 19:00 ngày 1/8 thuộc Cúp Liên Đoàn Anh."
-
-
Câu: "PSG sẽ đối đầu với Lille vào ngày 2/8 trong khuôn khổ vòng 1/8 của Cúp Quốc gia Pháp."
-
Lỗi sai: Đây là thông tin không chính xác vì PSG và Lille đối đầu trong trận Siêu Cúp Pháp, không phải Cúp Quốc gia Pháp.
-
Sửa lại: "PSG sẽ đối đầu với Lille vào ngày 2/8 trong trận Siêu Cúp Pháp."
-
Sau khi các em tìm thấy lỗi sai, hãy thử chỉnh sửa các câu trên để chúng trở nên chính xác hơn và viết lại câu hoàn chỉnh vào vở bài tập của mình.

Bài Tập 4: Viết Lại Câu Không Đổi Nghĩa
Trong bài tập này, bạn sẽ thực hành viết lại các câu để giữ nguyên nghĩa ban đầu nhưng sử dụng cấu trúc ngữ pháp khác. Hãy cố gắng thay đổi câu sao cho tự nhiên và chính xác nhất.
- Ví dụ 1:
- Câu gốc: "Hôm nay, lịch thi đấu bóng đá diễn ra vào lúc 18:00 với trận đấu giữa Trung Quốc và Anh."
- Câu viết lại: "Trận đấu giữa Trung Quốc và Anh sẽ diễn ra vào lúc 18:00 theo lịch thi đấu bóng đá hôm nay."
- Ví dụ 2:
- Câu gốc: "Trận đấu giữa PSG và Inter sẽ diễn ra lúc 17:00 hôm nay."
- Câu viết lại: "Lúc 17:00 hôm nay, trận đấu giữa PSG và Inter sẽ diễn ra."
Hãy viết lại các câu sau đây mà không làm thay đổi nghĩa của chúng:
- Lịch thi đấu bóng đá hôm nay có trận đấu giữa Bồ Đào Nha và Mỹ vào lúc 14:00.
- Trận đấu giữa Argentina và Fluminense sẽ diễn ra vào lúc 05:00 sáng ngày mai.
- Lúc 18:30 hôm nay, Union Saint Gilloise sẽ đối đầu với Club Brugge theo lịch thi đấu của giải VĐQG Bỉ.
Gợi ý: Bạn có thể thay đổi thứ tự các cụm từ hoặc sử dụng cấu trúc khác để câu vẫn giữ nguyên ý nghĩa ban đầu.
Bài Tập 5: Đọc Hiểu Văn Bản Tiếng Anh
Trong bài tập này, bạn sẽ thực hành kỹ năng đọc hiểu văn bản tiếng Anh qua việc phân tích một đoạn trích từ một bài viết về thể thao. Hãy thực hiện theo các bước dưới đây:
- Đọc kỹ đoạn văn: Đầu tiên, bạn hãy đọc đoạn văn một cách chậm rãi và chú ý đến từng từ vựng, ngữ pháp được sử dụng. Cố gắng hiểu nghĩa của từng câu một cách tổng thể.
- Ghi chú từ mới: Trong quá trình đọc, nếu gặp từ mới, hãy ghi chú lại và tra từ điển để hiểu nghĩa của từ trong ngữ cảnh.
- Phân tích câu hỏi: Sau khi đọc xong đoạn văn, bạn hãy đọc kỹ các câu hỏi bên dưới và xác định loại câu hỏi như câu hỏi thông tin chi tiết, câu hỏi suy luận, hay câu hỏi về từ vựng.
- Trả lời câu hỏi: Dựa vào nội dung đã đọc, bạn hãy trả lời các câu hỏi một cách chính xác nhất có thể. Đối với những câu hỏi khó, bạn có thể xem lại đoạn văn để tìm ra câu trả lời.
- Kiểm tra lại: Cuối cùng, hãy kiểm tra lại các câu trả lời của mình để chắc chắn rằng bạn đã hiểu đúng và trả lời chính xác.
Dưới đây là đoạn văn mẫu để bạn thực hành:
"In the match between Manchester City and Ipswich, the home team was dominant throughout the game. With multiple goals from key players, they secured a decisive victory. Despite the visitors' efforts, Manchester City's relentless attacks left them with no room to breathe."
Câu hỏi:
- 1. What was the outcome of the match?
- 2. How did Manchester City manage to dominate the game?
- 3. What challenges did Ipswich face during the match?
- 4. Which players contributed significantly to Manchester City's victory?
Hãy sử dụng kỹ năng đọc hiểu của bạn để trả lời các câu hỏi trên một cách chính xác nhất. Sau khi hoàn thành, bạn có thể so sánh kết quả với bạn bè hoặc giáo viên để nhận phản hồi.
Bài Tập 6: Sử Dụng Giới Từ Chính Xác
Trong tiếng Anh, giới từ là những từ dùng để liên kết giữa các từ, cụm từ trong câu và chỉ ra mối quan hệ giữa chúng. Để sử dụng giới từ chính xác, bạn cần nắm vững các quy tắc cơ bản và thực hành thường xuyên.
Dưới đây là một số ví dụ về cách sử dụng giới từ trong tiếng Anh:
- In: được dùng để chỉ vị trí bên trong một không gian hoặc thời gian dài.
- Ví dụ: in the room (trong phòng), in 2023 (vào năm 2023).
- On: được dùng để chỉ vị trí trên bề mặt hoặc ngày tháng cụ thể.
- Ví dụ: on the table (trên bàn), on Monday (vào thứ Hai).
- At: được dùng để chỉ thời điểm chính xác hoặc địa điểm cụ thể.
- Ví dụ: at 8 o'clock (vào lúc 8 giờ), at school (ở trường).
- By: được dùng để chỉ phương thức hoặc ai làm gì.
- Ví dụ: by car (bằng xe hơi), by John (bởi John).
Dưới đây là một số bài tập giúp bạn thực hành sử dụng giới từ chính xác:
- He lives ___ a small house ___ the countryside. (in/on/at)
- The meeting will start ___ 9 a.m. ___ Monday. (at/on)
- She arrived ___ the airport just ___ time for her flight. (at/in/on)
- I put the book ___ the shelf and the pen ___ the table. (on/in/at)
- He traveled ___ train to get here. (in/by/on)
Đáp án:
- He lives in a small house in the countryside.
- The meeting will start at 9 a.m. on Monday.
- She arrived at the airport just in time for her flight.
- I put the book on the shelf and the pen on the table.
- He traveled by train to get here.
Hãy tiếp tục luyện tập bằng cách tự tạo ra các câu có sử dụng giới từ. Điều này sẽ giúp bạn thành thạo hơn trong việc sử dụng giới từ trong tiếng Anh.
Bài Tập 7: Chọn Đáp Án Đúng Cho Câu Hoàn Chỉnh
Hãy chọn đáp án đúng để hoàn thành các câu sau đây về lịch thi đấu bóng đá ngày 1/8.
- Vào lúc 14:00 ngày 1/8, đội tuyển nào đã thi đấu trong khuôn khổ World Cup Nữ 2023?
- A. Bồ Đào Nha vs Mỹ
- B. Hà Lan vs Đan Mạch
- C. Nhật Bản vs Tây Ban Nha
- D. Trung Quốc vs Anh
- Trận đấu nào diễn ra lúc 18:00 cùng ngày giữa các đội tuyển ở World Cup Nữ?
- A. Đức vs Mỹ
- B. Hà Lan vs Pháp
- C. Trung Quốc vs Anh
- D. Argentina vs Brazil
- Đội nào đã thi đấu trong vòng sơ loại UEFA Champions League 2023/24 vào lúc 00:30 ngày 2/8?
- A. Panathinaikos vs Dnipro-1
- B. Real Madrid vs Manchester City
- C. Barcelona vs Juventus
- D. Bayern Munich vs Chelsea
- Trận đấu nào thuộc Copa Libertadores 2023 diễn ra vào lúc 05:00 ngày 2/8?
- A. Argentinos Juniors vs Fluminense
- B. Boca Juniors vs River Plate
- C. Palmeiras vs Flamengo
- D. Atletico Mineiro vs Sao Paulo
Hãy chọn đáp án đúng và ghi vào giấy để kiểm tra kết quả cuối cùng của bạn!
Bài Tập 8: Phân Biệt Các Thì Tiếp Diễn Và Đơn
Trong tiếng Anh, việc phân biệt giữa các thì tiếp diễn và thì đơn rất quan trọng để hiểu rõ về ngữ cảnh cũng như thời gian xảy ra của một hành động. Dưới đây là một số điểm quan trọng cần lưu ý khi phân biệt hai thì này:
1. Thì Hiện Tại Đơn (Present Simple)
- Diễn tả hành động xảy ra thường xuyên hoặc lặp lại.
- Diễn tả sự thật hiển nhiên, chân lý.
- Công thức:
- Khẳng định: S + V(s/es) + O
- Phủ định: S + do/does not + V + O
- Nghi vấn: Do/Does + S + V + O?
- Ví dụ:
- He plays football every Sunday.
- The sun rises in the East.
2. Thì Hiện Tại Tiếp Diễn (Present Continuous)
- Diễn tả hành động đang diễn ra ngay tại thời điểm nói.
- Diễn tả hành động tạm thời, không kéo dài mãi mãi.
- Công thức:
- Khẳng định: S + am/is/are + V-ing + O
- Phủ định: S + am/is/are not + V-ing + O
- Nghi vấn: Am/Is/Are + S + V-ing + O?
- Ví dụ:
- She is playing football now.
- We are learning English this week.
3. Thì Quá Khứ Đơn (Past Simple)
- Diễn tả hành động đã xảy ra và kết thúc trong quá khứ.
- Công thức:
- Khẳng định: S + V2/V-ed + O
- Phủ định: S + did not + V + O
- Nghi vấn: Did + S + V + O?
- Ví dụ:
- They visited Da Nang last year.
- I watched that movie yesterday.
4. Thì Quá Khứ Tiếp Diễn (Past Continuous)
- Diễn tả hành động đang diễn ra tại một thời điểm cụ thể trong quá khứ.
- Diễn tả hành động đang diễn ra thì một hành động khác chen vào.
- Công thức:
- Khẳng định: S + was/were + V-ing + O
- Phủ định: S + was/were not + V-ing + O
- Nghi vấn: Was/Were + S + V-ing + O?
- Ví dụ:
- He was playing football at 3 p.m. yesterday.
- While I was reading, she called me.
5. Thì Tương Lai Đơn (Future Simple)
- Diễn tả hành động sẽ xảy ra trong tương lai.
- Công thức:
- Khẳng định: S + will + V + O
- Phủ định: S + will not + V + O
- Nghi vấn: Will + S + V + O?
- Ví dụ:
- They will play football tomorrow.
- We will go to the beach next week.
6. Thì Tương Lai Tiếp Diễn (Future Continuous)
- Diễn tả hành động sẽ đang diễn ra tại một thời điểm cụ thể trong tương lai.
- Công thức:
- Khẳng định: S + will be + V-ing + O
- Phủ định: S + will not be + V-ing + O
- Nghi vấn: Will + S + be + V-ing + O?
- Ví dụ:
- At this time tomorrow, they will be playing football.
- We will be flying to Da Nang at 8 a.m. next week.
7. Bài Tập Thực Hành
- He (play) football every day. (Thì hiện tại đơn)
- They (watch) a movie now. (Thì hiện tại tiếp diễn)
- I (go) to Da Nang last year. (Thì quá khứ đơn)
- We (study) English when you called. (Thì quá khứ tiếp diễn)
- She (travel) to Japan next month. (Thì tương lai đơn)
- They (have) a meeting at this time tomorrow. (Thì tương lai tiếp diễn)
Bài Tập 9: Dịch Văn Bản Ngắn Sang Tiếng Anh
Trong bài tập này, bạn sẽ luyện tập kỹ năng dịch một đoạn văn ngắn từ tiếng Việt sang tiếng Anh. Để làm tốt bài tập, bạn cần nắm rõ ngữ pháp cơ bản, từ vựng, và cấu trúc câu trong cả hai ngôn ngữ. Dưới đây là quy trình dịch theo từng bước:
- Đọc hiểu đoạn văn: Hãy đọc kỹ đoạn văn bằng tiếng Việt để hiểu rõ nội dung, ý chính và các chi tiết phụ.
- Ghi chú từ vựng: Đối với những từ khó hoặc từ chuyên ngành, hãy tra từ điển để ghi chú nghĩa và cách dùng trong ngữ cảnh.
- Dịch câu theo nghĩa: Dịch từng câu theo đúng ngữ cảnh, không dịch từng từ riêng lẻ để tránh sai nghĩa.
- Kiểm tra ngữ pháp: Đảm bảo rằng câu dịch có ngữ pháp tiếng Anh đúng chuẩn, bao gồm các thì và cách chia động từ chính xác.
- So sánh và chỉnh sửa: Sau khi dịch xong, hãy so sánh với bản gốc để kiểm tra tính chính xác và sự mạch lạc của đoạn văn.
Ví dụ: Hãy dịch đoạn văn sau từ tiếng Việt sang tiếng Anh:
"Lịch thi đấu bóng đá ngày 1/8 có nhiều trận đấu hấp dẫn ở các giải đấu lớn như UEFA Europa League, V.League và Ngoại hạng Anh. Người hâm mộ đang rất mong chờ những trận đấu gay cấn sắp diễn ra."
Đáp án tham khảo:
"The football schedule on August 1st includes many exciting matches in major tournaments such as the UEFA Europa League, V.League, and Premier League. Fans are eagerly awaiting the thrilling matches to come."
Giải thích: Trong câu này, "Lịch thi đấu" được dịch là "The football schedule", "ngày 1/8" là "on August 1st". "Trận đấu hấp dẫn" là "exciting matches" và "giải đấu lớn" được dịch là "major tournaments". Chú ý rằng các thì trong câu cũng đã được chuyển đúng sang tiếng Anh.
Hãy luyện tập dịch các đoạn văn ngắn mỗi ngày để nâng cao kỹ năng dịch thuật của bạn!
Bài Tập 10: Đặt Câu Hỏi Với Từ Được Gạch Chân
Trong bài tập này, bạn sẽ luyện tập kỹ năng đặt câu hỏi với từ hoặc cụm từ được gạch chân trong câu. Điều này giúp bạn cải thiện khả năng hiểu câu và cách dùng các dạng câu hỏi trong tiếng Anh.
Quy trình thực hiện:
- Đọc kỹ câu cho sẵn và xác định từ hoặc cụm từ được gạch chân.
- Xác định loại từ (danh từ, động từ, trạng từ, tính từ, ...) của từ được gạch chân để chọn dạng câu hỏi phù hợp.
- Đặt câu hỏi với từ gạch chân bằng cách sử dụng các từ để hỏi như: Who, What, Where, When, Why, How,...
Ví dụ:
Cho câu sau: "He will play football next Sunday."
- Từ được gạch chân: next Sunday
- Câu hỏi đặt ra: "When will he play football?"
Bài tập:
Đặt câu hỏi với từ được gạch chân trong các câu sau:
- 1. They are going to the stadium.
- 2. She bought a new shirt yesterday.
- 3. The match will start at 6 PM.
- 4. He plays football every weekend.
- 5. They live in Paris.
Đáp án tham khảo:
- 1. Where are they going?
- 2. What did she buy yesterday?
- 3. When will the match start?
- 4. How often does he play football?
- 5. Where do they live?
Hãy luyện tập đặt câu hỏi hàng ngày để nâng cao khả năng sử dụng câu hỏi trong giao tiếp tiếng Anh của bạn!