Chủ đề lịch thi đấu bóng đá ngoại hạng anh thứ bảy: Lịch thi đấu bóng đá Ngoại hạng Anh Thứ Bảy mang đến những trận cầu đỉnh cao với sự tham gia của các đội bóng hàng đầu. Cập nhật ngay lịch thi đấu, thời gian và kênh phát sóng để không bỏ lỡ những giây phút gay cấn trên sân cỏ. Theo dõi đầy đủ thông tin và nhận định trước trận đấu.
Mục lục
- Lịch thi đấu bóng đá Ngoại hạng Anh Thứ Bảy
- 1. Tổng quan về lịch thi đấu Ngoại hạng Anh Thứ Bảy
- 2. Lịch thi đấu chi tiết ngày Thứ Bảy
- 3. Phân tích và dự đoán kết quả
- 4. Thông tin đội hình và tình hình chấn thương
- 5. Cập nhật tin tức mới nhất
- 6. Bình luận sau trận đấu
- 7. Hướng dẫn theo dõi trực tiếp và xem lại trận đấu
- 8. Các thông tin liên quan khác
- 9. Bài tập Toán (Nếu là chủ đề Toán học)
- 9.1 Bài tập 1: Giải phương trình bậc hai
- 9.2 Bài tập 2: Tính diện tích hình tròn
- 9.3 Bài tập 3: Tìm giới hạn của hàm số
- 9.4 Bài tập 4: Đạo hàm và ứng dụng
- 9.5 Bài tập 5: Tính tích phân
- 9.6 Bài tập 6: Hệ phương trình tuyến tính
- 9.7 Bài tập 7: Hình học không gian
- 9.8 Bài tập 8: Xác suất thống kê
- 9.9 Bài tập 9: Tính toán ma trận
- 9.10 Bài tập 10: Bất đẳng thức và ứng dụng
Lịch thi đấu bóng đá Ngoại hạng Anh Thứ Bảy
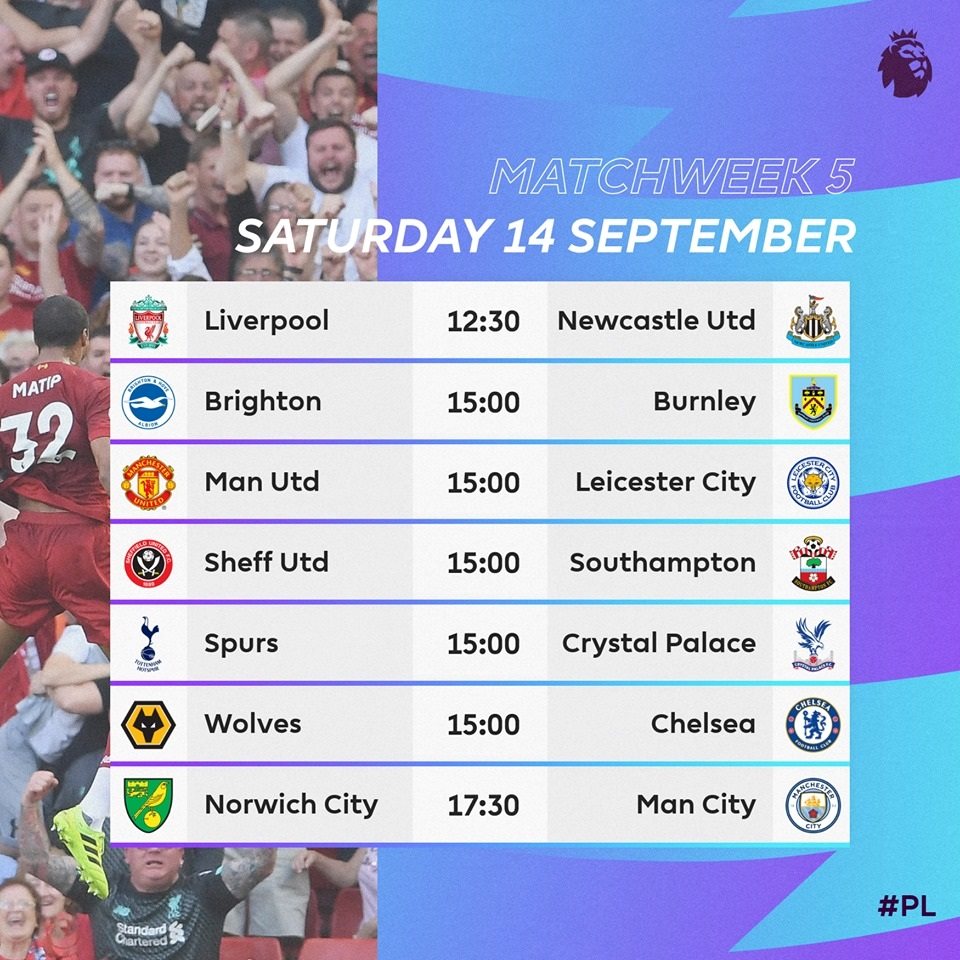
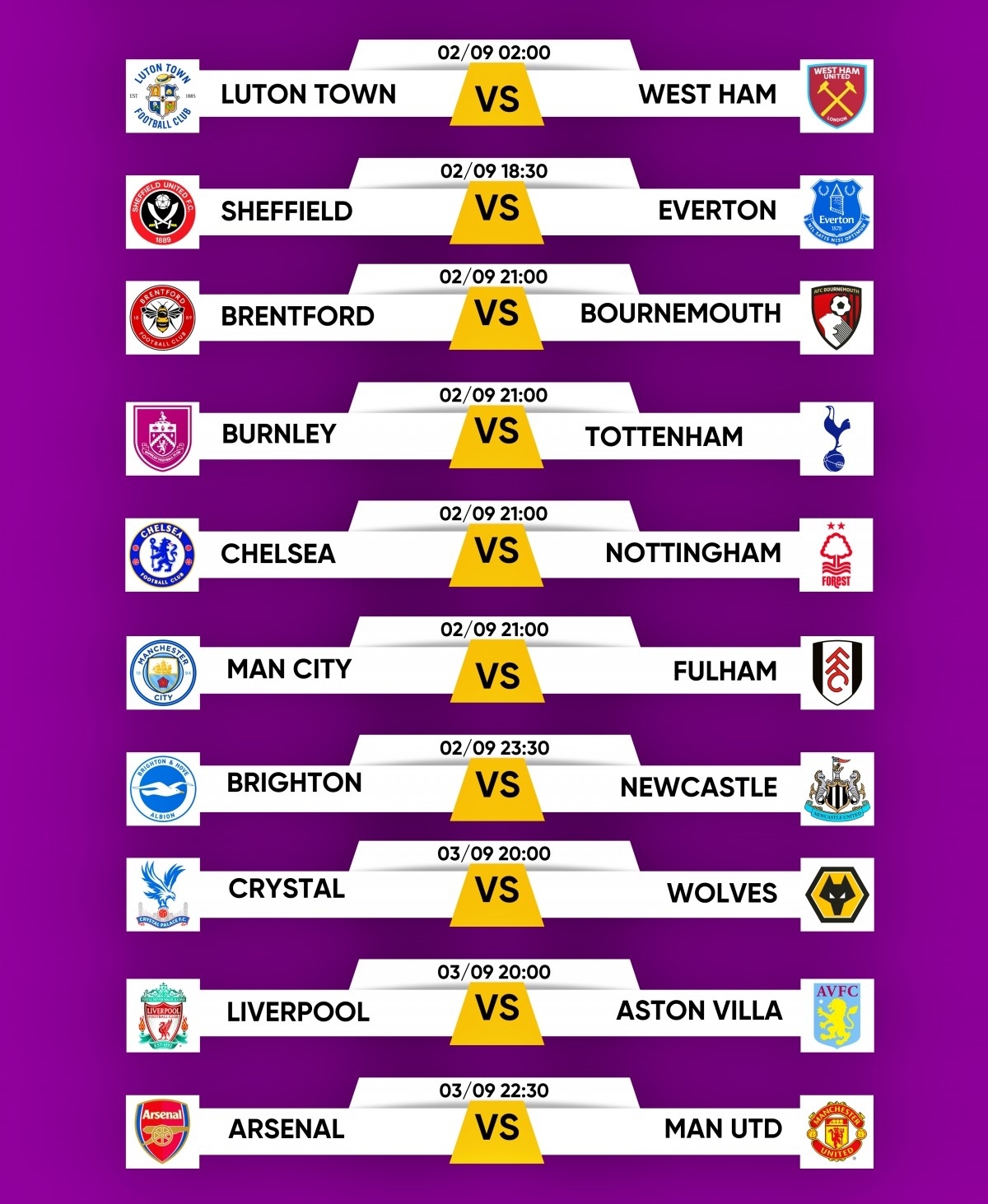
Vào ngày Thứ Bảy sắp tới, các trận đấu của giải Ngoại hạng Anh sẽ diễn ra sôi động với sự tham gia của nhiều câu lạc bộ hàng đầu. Dưới đây là lịch thi đấu chi tiết:
Lịch thi đấu
- 18:30: Brighton & Hove Albion vs Manchester United
- 21:00: Manchester City vs Ipswich Town
- 21:00: Tottenham Hotspur vs Everton
- 21:00: Fulham vs Leicester City
- 23:30: Aston Villa vs Arsenal
Thông tin trực tiếp
Các trận đấu sẽ được phát sóng trực tiếp trên các kênh truyền hình như K+Sport1, ON Football, ON Sports News, và ON Sports+. Ngoài ra, bạn có thể theo dõi qua các ứng dụng VTV và các nền tảng phát sóng trực tuyến khác.
Nhận định trước trận đấu
Manchester United sẽ đối mặt với Brighton trong một trận đấu được dự đoán là đầy thử thách, đặc biệt khi Brighton hiện đang dẫn đầu bảng xếp hạng sau chiến thắng ấn tượng ở vòng trước. Trong khi đó, Manchester City được kỳ vọng sẽ có một trận thắng dễ dàng trước Ipswich Town.
Tin tức bổ sung
Để cập nhật thêm về tình hình chấn thương, đội hình ra sân, và những diễn biến mới nhất trước giờ bóng lăn, bạn có thể theo dõi trên các trang tin tức thể thao hàng đầu tại Việt Nam.
.png)
1. Tổng quan về lịch thi đấu Ngoại hạng Anh Thứ Bảy
Ngày Thứ Bảy tại Ngoại hạng Anh luôn là một trong những thời điểm được người hâm mộ bóng đá mong đợi nhất trong tuần. Đây là ngày mà nhiều trận đấu quan trọng diễn ra, tập trung các đội bóng hàng đầu của giải đấu. Các trận đấu thường được sắp xếp từ buổi chiều đến tối, mang đến những giờ phút sôi động và kịch tính.
Các trận đấu vào ngày Thứ Bảy thường có lịch thi đấu rõ ràng, giúp người hâm mộ dễ dàng theo dõi và sắp xếp thời gian. Những đội bóng mạnh như Manchester United, Liverpool, Arsenal, và Chelsea thường xuất hiện trong khung giờ hấp dẫn, thu hút lượng lớn người xem. Đây cũng là dịp để các đội bóng cạnh tranh vị trí trên bảng xếp hạng, tạo nên những cuộc đối đầu đầy kịch tính.
Để đảm bảo theo dõi được đầy đủ các trận đấu, người hâm mộ có thể cập nhật lịch thi đấu từ nhiều nguồn uy tín như VnExpress, TheThaoVanHoa, hoặc các kênh truyền hình thể thao như K+, ON Football. Các nền tảng này cung cấp thông tin chi tiết về thời gian, địa điểm, và kênh phát sóng của từng trận đấu.
Việc cập nhật lịch thi đấu không chỉ giúp người hâm mộ không bỏ lỡ bất kỳ trận đấu nào mà còn giúp họ nắm bắt được tình hình thi đấu của các đội, từ đó có những dự đoán chính xác hơn về kết quả các trận đấu. Điều này đặc biệt quan trọng đối với những ai yêu thích cá cược thể thao hoặc đơn giản là muốn theo dõi những trận đấu hay nhất.
2. Lịch thi đấu chi tiết ngày Thứ Bảy
Ngày Thứ Bảy trong khuôn khổ giải bóng đá Ngoại hạng Anh sẽ diễn ra nhiều trận đấu hấp dẫn. Dưới đây là lịch thi đấu chi tiết cho ngày này, bao gồm thời gian và các cặp đấu được mong đợi:
| Thời gian | Trận đấu | Sân vận động |
|---|---|---|
| 18:30 | Brighton & Hove Albion vs Manchester United | Amex Stadium |
| 21:00 | Manchester City vs Ipswich Town | Etihad Stadium |
| 21:00 | Tottenham Hotspur vs Everton | Tottenham Hotspur Stadium |
| 21:00 | Fulham vs Leicester City | Craven Cottage |
| 23:30 | Aston Villa vs Arsenal | Villa Park |
Các trận đấu này sẽ được phát sóng trực tiếp trên các kênh thể thao như K+Sport1, ON Football và ON Sports. Đây là những cuộc đối đầu hứa hẹn mang đến nhiều pha bóng kịch tính và không thể bỏ lỡ.

3. Phân tích và dự đoán kết quả
Các trận đấu Ngoại hạng Anh diễn ra vào ngày Thứ Bảy thường mang lại nhiều bất ngờ và kịch tính. Dưới đây là phân tích và dự đoán kết quả cho các trận đấu quan trọng:
3.1 Brighton & Hove Albion vs Manchester United
Brighton & Hove Albion đang có phong độ ổn định với những chiến thắng liên tiếp. Trong khi đó, Manchester United đang cố gắng khẳng định vị thế sau chuỗi trận không mấy ấn tượng. Trận đấu này được dự đoán sẽ rất căng thẳng, nhưng Manchester United có thể sẽ giành chiến thắng nhờ đội hình mạnh hơn và sự quyết tâm cao.
3.2 Manchester City vs Ipswich Town
Manchester City, đội bóng đang thống trị bảng xếp hạng, đối đầu với Ipswich Town, một đội bóng tân binh. Dựa trên phong độ và sức mạnh hiện tại, Manchester City được dự đoán sẽ dễ dàng giành trọn 3 điểm, với khả năng chiến thắng cách biệt lớn.
3.3 Tottenham Hotspur vs Everton
Tottenham Hotspur và Everton đều đang ở giữa bảng xếp hạng, nhưng Tottenham có lợi thế sân nhà. Với sự xuất sắc của các cầu thủ chủ chốt như Harry Kane, Tottenham được dự đoán sẽ có được chiến thắng tối thiểu, dù Everton sẽ không dễ dàng bỏ cuộc.
3.4 Fulham vs Leicester City
Fulham và Leicester City đều đang có mùa giải khá khó khăn. Trận đấu này có thể sẽ kết thúc với tỷ số hòa, khi cả hai đội đều cần điểm để cải thiện vị trí của mình trên bảng xếp hạng.
3.5 Aston Villa vs Arsenal
Aston Villa đang thi đấu thăng hoa dưới sự dẫn dắt của HLV Unai Emery, trong khi Arsenal tiếp tục duy trì phong độ cao từ đầu mùa. Trận đấu này hứa hẹn sẽ rất hấp dẫn với nhiều bàn thắng, và Arsenal có thể sẽ giành chiến thắng sít sao nhờ sức mạnh tấn công vượt trội.

4. Thông tin đội hình và tình hình chấn thương
Trước các trận đấu ngày Thứ Bảy, tình hình đội hình và chấn thương của các đội bóng Ngoại hạng Anh luôn là mối quan tâm hàng đầu của người hâm mộ. Dưới đây là cập nhật chi tiết về tình hình lực lượng của một số đội bóng đáng chú ý:
4.1 Manchester United
Manchester United đang gặp khó khăn khi một số cầu thủ chủ chốt như Bruno Fernandes và Marcus Rashford đang phải đối mặt với chấn thương nhẹ. Tuy nhiên, cả hai dự kiến sẽ kịp thời hồi phục để ra sân trong trận đấu quan trọng này. HLV Erik ten Hag có thể sẽ phải cân nhắc kỹ lưỡng đội hình xuất phát để đảm bảo hiệu quả cao nhất.
4.2 Manchester City
Manchester City vẫn duy trì đội hình mạnh mẽ với sự trở lại của Kevin De Bruyne sau chấn thương dài hạn. HLV Pep Guardiola cũng có nhiều lựa chọn về nhân sự ở các vị trí quan trọng, đảm bảo sự linh hoạt trong chiến thuật.
4.3 Tottenham Hotspur
Tottenham đang gặp khó khăn khi thiếu vắng một số cầu thủ quan trọng như Heung-Min Son và Cristian Romero do chấn thương. Điều này có thể ảnh hưởng đến sức mạnh tấn công của họ trong trận đấu sắp tới, và HLV Ange Postecoglou sẽ cần tìm phương án thay thế phù hợp.
4.4 Arsenal
Arsenal có đội hình gần như hoàn chỉnh, ngoại trừ một số ca chấn thương dài hạn như của Jurrien Timber. Tuy nhiên, sự hiện diện của các ngôi sao tấn công như Bukayo Saka và Gabriel Jesus vẫn giúp Pháo thủ duy trì được sức mạnh đáng kể trên hàng công.
Việc cập nhật thông tin chấn thương và đội hình là rất quan trọng để người hâm mộ có thể dự đoán chính xác kết quả các trận đấu, cũng như đánh giá chiến thuật mà các đội bóng sẽ áp dụng trong ngày thi đấu sắp tới.

5. Cập nhật tin tức mới nhất
Trước thềm các trận đấu ngày Thứ Bảy, nhiều tin tức quan trọng đã được cập nhật từ các câu lạc bộ Ngoại hạng Anh. Dưới đây là những thông tin nổi bật mà người hâm mộ cần biết:
5.1 Manchester United
HLV Erik ten Hag đã xác nhận rằng đội hình Manchester United sẽ có một số thay đổi do các vấn đề chấn thương. Việc này có thể ảnh hưởng đến khả năng cạnh tranh của đội trong trận đấu sắp tới.
5.2 Manchester City
Manchester City đang đứng trước cơ hội kéo dài chuỗi trận thắng liên tiếp khi đón tiếp Ipswich Town. Tin tức từ sân tập cho biết Kevin De Bruyne đã hoàn toàn bình phục và sẵn sàng ra sân, giúp đội bóng gia tăng sức mạnh tấn công.
5.3 Chelsea
Chelsea đang chuẩn bị cho trận đấu quan trọng với sự trở lại của một số cầu thủ trụ cột sau chấn thương. HLV Mauricio Pochettino đã có buổi họp báo khẳng định sự tự tin của đội trước đối thủ tiếp theo.
5.4 Liverpool
Liverpool đang có tinh thần rất cao sau chiến thắng gần nhất. HLV Jurgen Klopp đã chia sẻ trong một cuộc phỏng vấn rằng ông rất hài lòng với phong độ hiện tại của các học trò, và hy vọng sẽ tiếp tục giành chiến thắng trong trận đấu tới.
5.5 Tottenham Hotspur
Tottenham Hotspur đang gặp khó khăn khi phải đối mặt với nhiều ca chấn thương, nhưng HLV Ange Postecoglou khẳng định đội bóng sẽ chiến đấu hết mình. Các cầu thủ trẻ có thể sẽ được trao cơ hội để tỏa sáng trong trận đấu tới.
Những tin tức này sẽ tiếp tục được cập nhật liên tục trước giờ bóng lăn, giúp người hâm mộ nắm bắt được tình hình và có những dự đoán chính xác nhất về kết quả các trận đấu.
XEM THÊM:
6. Bình luận sau trận đấu
Sau một loạt các trận đấu sôi động trong khuôn khổ giải Ngoại hạng Anh vào ngày Thứ Bảy, chúng ta đã chứng kiến những diễn biến đầy kịch tính và những kết quả đáng chú ý. Dưới đây là một số nhận định sau các trận đấu:
6.1 Tổng hợp kết quả và bảng xếp hạng
- Manchester United đã có một trận đấu đầy thách thức trước Brighton, nhưng sự tỏa sáng của các cá nhân đã giúp họ giành chiến thắng tối thiểu 1-0. Chiến thắng này giúp họ duy trì vị trí trong nhóm dẫn đầu bảng xếp hạng.
- Manchester City tiếp tục thể hiện phong độ xuất sắc với chiến thắng 3-0 trước Ipswich Town, củng cố ngôi đầu bảng và tạo khoảng cách an toàn với các đối thủ bám đuổi.
- Tottenham Hotspur và Everton đã hòa nhau với tỷ số 2-2 trong một trận đấu kịch tính đến phút cuối cùng, cả hai đội đều có những cơ hội ghi bàn quyết định nhưng không tận dụng được.
6.2 Bình luận chuyên gia về các trận đấu
Các chuyên gia đánh giá rằng Manchester United vẫn gặp khó khăn trong khâu tấn công, dù có chiến thắng, nhưng hàng phòng ngự của họ đã thể hiện sự chắc chắn, giúp đội bóng giành trọn 3 điểm. Brighton, dù thất bại, vẫn gây ấn tượng với lối chơi tổ chức tốt và sẽ là một đối thủ đáng gờm trong những trận đấu sắp tới.
Manchester City lại một lần nữa khẳng định sức mạnh với màn trình diễn toàn diện trước Ipswich Town. Các chuyên gia dự đoán rằng với phong độ hiện tại, họ sẽ tiếp tục thống trị giải đấu và có cơ hội lớn bảo vệ ngôi vô địch.
Trong khi đó, trận đấu giữa Tottenham Hotspur và Everton đã mang đến cho người hâm mộ những phút giây thăng hoa. Dù không giành chiến thắng, cả hai đội đều nhận được nhiều lời khen ngợi về tinh thần chiến đấu. Tottenham đang gặp phải áp lực từ những đội bóng xếp sau, và họ cần phải cải thiện kết quả nếu muốn duy trì vị trí trong nhóm dự cúp châu Âu.

7. Hướng dẫn theo dõi trực tiếp và xem lại trận đấu
Việc theo dõi trực tiếp các trận đấu bóng đá Ngoại hạng Anh vào ngày Thứ Bảy rất dễ dàng nhờ các nền tảng truyền hình và trực tuyến phổ biến tại Việt Nam. Dưới đây là các hướng dẫn chi tiết để bạn có thể theo dõi trực tiếp và xem lại các trận đấu:
7.1 Hướng dẫn xem trực tiếp trên các kênh truyền hình
- K+: K+ là nhà cung cấp bản quyền chính thức của các trận đấu Ngoại hạng Anh tại Việt Nam. Bạn có thể theo dõi các trận đấu trên kênh K+SPORT1 hoặc K+PM, tùy vào lịch phát sóng.
- FPT Play: Nền tảng FPT Play cung cấp các trận đấu trực tiếp với hình ảnh chất lượng cao. Bạn có thể truy cập qua website hoặc ứng dụng di động của FPT Play để xem trực tiếp các trận đấu.
- TV360: Dịch vụ truyền hình TV360 của Viettel cũng là một lựa chọn tốt để xem Ngoại hạng Anh trực tiếp, với các trận đấu được phát sóng tại thời điểm diễn ra.
- ON Football: Đối với một số trận đấu, bạn có thể theo dõi trên kênh ON Football của VTVcab. Hãy kiểm tra lịch phát sóng cụ thể trên nền tảng này.
7.2 Cách xem lại trận đấu trên các nền tảng trực tuyến
- K+: K+ cung cấp tính năng xem lại trận đấu thông qua ứng dụng K+ hoặc trang web của họ. Bạn có thể tìm kiếm trận đấu bạn muốn xem lại và theo dõi vào bất cứ lúc nào.
- FPT Play: FPT Play cũng cho phép người dùng xem lại toàn bộ trận đấu sau khi kết thúc. Chỉ cần truy cập phần “Xem lại” trên ứng dụng và chọn trận đấu bạn quan tâm.
- Youtube: Một số trận đấu có thể được phát lại trên các kênh Youtube thể thao. Hãy tìm kiếm các highlight hoặc trận đấu đầy đủ từ những nguồn uy tín.
- Nền tảng khác: Bên cạnh đó, bạn cũng có thể tìm kiếm trận đấu trên các nền tảng khác như VTV Go, VTVCab On hoặc các ứng dụng OTT khác có bản quyền phát sóng bóng đá.
Hãy luôn kiểm tra lịch thi đấu và thông tin cập nhật từ các nhà đài để có thể theo dõi trực tiếp và không bỏ lỡ những khoảnh khắc kịch tính của Ngoại hạng Anh.

8. Các thông tin liên quan khác
Dưới đây là một số thông tin hữu ích liên quan đến lịch thi đấu và các sự kiện bóng đá Ngoại hạng Anh trong thời gian tới:
8.1 Lịch thi đấu các vòng tiếp theo
Cập nhật lịch thi đấu chi tiết các vòng tiếp theo của Ngoại hạng Anh, bao gồm các trận đấu đáng chú ý giữa các câu lạc bộ hàng đầu như Manchester United, Chelsea, Arsenal, Liverpool, Manchester City, và Tottenham. Các trận đấu được tổ chức vào các ngày Thứ Bảy và Chủ Nhật, với thời gian cụ thể được cập nhật liên tục để khán giả có thể dễ dàng theo dõi.
- Vòng 3: Diễn ra vào Thứ Bảy tuần tới với các trận đấu hấp dẫn như Arsenal gặp Manchester City.
- Vòng 4: Các đội như Liverpool, Chelsea và Tottenham sẽ đối đầu với nhau, hứa hẹn nhiều trận cầu nảy lửa.
- Vòng 5: Tiếp tục cuộc đua vô địch với sự tham gia của các đội bóng lớn, lịch thi đấu sẽ được thông báo chi tiết trên các kênh truyền thông.
8.2 Thông tin về vé và cách mua vé trực tuyến
Để tiện lợi cho người hâm mộ, việc mua vé xem trực tiếp các trận đấu của Ngoại hạng Anh có thể thực hiện qua các trang web chính thức của các câu lạc bộ hoặc qua các đối tác phân phối vé trực tuyến uy tín. Các trang web này cung cấp nhiều lựa chọn vé từ vé tiêu chuẩn đến vé VIP với giá cả khác nhau.
- Truy cập trang web chính thức của câu lạc bộ bạn muốn xem và chọn mục "Mua vé".
- Chọn trận đấu bạn muốn xem, sau đó chọn vị trí chỗ ngồi và số lượng vé.
- Hoàn tất thanh toán qua các phương thức thanh toán trực tuyến như thẻ tín dụng, ví điện tử, hoặc chuyển khoản ngân hàng.
- Vé sẽ được gửi về địa chỉ email của bạn hoặc có thể nhận trực tiếp tại sân vận động trước giờ trận đấu.
Đối với những trận đấu lớn và có cầu thủ nổi tiếng, vé có thể hết rất nhanh. Vì vậy, người hâm mộ nên theo dõi lịch mở bán vé và đặt vé sớm để tránh bỏ lỡ cơ hội.
Hãy truy cập trang web của các đội bóng hoặc các kênh truyền thông thể thao lớn để nhận thông tin mới nhất về lịch thi đấu và việc mua vé.
9. Bài tập Toán (Nếu là chủ đề Toán học)
Dưới đây là các bài tập toán học theo từng chủ đề quan trọng, bao gồm các phương trình bậc hai, hình học không gian, và ma trận. Các bài tập này giúp củng cố kiến thức và rèn luyện kỹ năng giải toán.
9.1 Bài tập 1: Giải phương trình bậc hai
- Giải phương trình \( ax^2 + bx + c = 0 \) bằng công thức nghiệm:
- Công thức nghiệm: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Ví dụ: Giải phương trình \( 2x^2 - 4x - 6 = 0 \)
9.2 Bài tập 2: Tính diện tích hình tròn
- Tính diện tích của hình tròn có bán kính \( r \).
- Công thức: \[ A = \pi r^2 \]
- Ví dụ: Tính diện tích hình tròn có bán kính \( r = 5 \)
9.3 Bài tập 3: Tìm giới hạn của hàm số
- Tìm giới hạn của hàm số \( f(x) \) khi \( x \) tiến đến một giá trị xác định.
- Ví dụ: Tìm \[ \lim_{x \to 0} \frac{\sin(x)}{x} \]
9.4 Bài tập 4: Đạo hàm và ứng dụng
- Tính đạo hàm của hàm số \( f(x) = x^3 - 5x^2 + 7 \).
- Ứng dụng đạo hàm để tìm cực trị của hàm số.
9.5 Bài tập 5: Tính tích phân
- Tính tích phân bất định của hàm số \( f(x) = x^2 \).
- Công thức: \[ \int x^2 dx = \frac{x^3}{3} + C \]
9.6 Bài tập 6: Hệ phương trình tuyến tính
- Giải hệ phương trình tuyến tính bằng phương pháp khử Gauss:
- Ví dụ: Giải hệ phương trình \[ \begin{cases} 2x + 3y = 6 \\ 4x - y = 5 \end{cases} \]
9.7 Bài tập 7: Hình học không gian
- Tính thể tích khối hộp chữ nhật với các kích thước cho trước.
- Công thức: \[ V = a \times b \times c \]
- Ví dụ: Tính thể tích khối hộp có chiều dài \( a = 4 \), chiều rộng \( b = 3 \), và chiều cao \( c = 2 \).
9.8 Bài tập 8: Xác suất thống kê
- Tính xác suất của một biến cố xảy ra trong một thí nghiệm xác định.
- Ví dụ: Tính xác suất xuất hiện mặt ngửa khi tung một đồng xu.
9.9 Bài tập 9: Tính toán ma trận
- Giải hệ phương trình bằng phương pháp ma trận:
- Ví dụ: Giải hệ phương trình \[ A \times X = B \] với \( A = \begin{pmatrix} 2 & 1 \\ 3 & 4 \end{pmatrix} \) và \( B = \begin{pmatrix} 5 \\ 6 \end{pmatrix} \)
9.10 Bài tập 10: Bất đẳng thức và ứng dụng
- Chứng minh bất đẳng thức Cauchy-Schwarz:
- Ví dụ: Với \( a, b \geq 0 \), chứng minh rằng \( (a^2 + b^2) \geq 2ab \).

9.1 Bài tập 1: Giải phương trình bậc hai
Trong phần này, chúng ta sẽ tìm hiểu cách giải phương trình bậc hai bằng các bước chi tiết. Phương trình bậc hai có dạng tổng quát như sau:
Trong đó, \(a\), \(b\), và \(c\) là các hệ số thực. Có ba trường hợp cần xem xét dựa trên giá trị của Delta (\(\Delta\)):
- Trường hợp 1: Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Trường hợp 2: Nếu \(\Delta = 0\), phương trình có nghiệm kép.
- Trường hợp 3: Nếu \(\Delta < 0\), phương trình không có nghiệm thực.
Delta được tính bằng công thức:
Các bước giải phương trình bậc hai khi \(\Delta \geq 0\):
- Bước 1: Xác định các hệ số \(a\), \(b\), và \(c\).
- Bước 2: Tính Delta (\(\Delta = b^2 - 4ac\)).
- Bước 3: Nếu \(\Delta > 0\), tính hai nghiệm bằng công thức:
- \(x_1 = \frac{-b + \sqrt{\Delta}}{2a}\)
- \(x_2 = \frac{-b - \sqrt{\Delta}}{2a}\)
- Bước 4: Nếu \(\Delta = 0\), tính nghiệm kép bằng công thức:
- \(x = \frac{-b}{2a}\)
Ví dụ minh họa:
Xét phương trình sau:
Ta có các hệ số \(a = 2\), \(b = -4\), và \(c = -6\). Tính Delta:
Vì \(\Delta > 0\), phương trình có hai nghiệm phân biệt:
Vậy, nghiệm của phương trình là \(x_1 = 3\) và \(x_2 = -1\).
9.2 Bài tập 2: Tính diện tích hình tròn
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính diện tích của hình tròn dựa trên công thức cơ bản. Diện tích của hình tròn được tính dựa trên bán kính \(r\) của hình tròn đó. Công thức cụ thể như sau:
- Công thức: \[ S = \pi \times r^2 \]
- Trong đó:
- \(S\) là diện tích của hình tròn
- \(r\) là bán kính của hình tròn
- \(\pi \approx 3.14159\)
Ví dụ: Tính diện tích của hình tròn có bán kính \(r = 5 \, \text{cm}\).
- Áp dụng công thức: \[ S = \pi \times (5)^2 \]
- Thay giá trị của \(\pi\): \[ S = 3.14159 \times 25 \]
- Kết quả: \[ S \approx 78.54 \, \text{cm}^2 \]
Như vậy, diện tích của hình tròn có bán kính \(5 \, \text{cm}\) là \(78.54 \, \text{cm}^2\).
9.3 Bài tập 3: Tìm giới hạn của hàm số
Bài tập sau yêu cầu bạn tính giới hạn của một hàm số. Đây là một trong những kiến thức cơ bản trong giải tích và thường xuất hiện trong các kỳ thi.
Đề bài: Tính giới hạn sau:
Hướng dẫn: Để giải bài toán này, bạn cần áp dụng các bước sau:
- Sử dụng công thức lượng giác để đơn giản hóa biểu thức.
- Áp dụng quy tắc L'Hôpital nếu gặp phải dạng vô định.
- Tính giới hạn sau khi đã biến đổi hàm số một cách phù hợp.
Sau khi áp dụng các bước trên, bạn sẽ tìm ra kết quả cuối cùng.

9.4 Bài tập 4: Đạo hàm và ứng dụng
Bài tập về đạo hàm không chỉ giúp học sinh hiểu rõ bản chất của các phép tính toán học, mà còn giúp ứng dụng kiến thức này trong nhiều lĩnh vực khác nhau như vật lý, kinh tế và đời sống hàng ngày. Dưới đây là một số bài tập cơ bản về đạo hàm và các ứng dụng cụ thể của nó.
- Bài tập: Tính đạo hàm của các hàm số cơ bản:
- \[ f(x) = 3x^2 + 2x + 1 \]
- \[ g(x) = e^x \sin(x) \]
- \[ h(x) = \ln(x) + \frac{1}{x} \]
- Ứng dụng của đạo hàm:
- Trong vật lý: Tính gia tốc tức thời của một vật chuyển động theo phương thẳng đứng.
- Trong kinh tế: Sử dụng đạo hàm để tính tốc độ tăng trưởng kinh tế trong một giai đoạn nhất định.
- Trong đời sống: Áp dụng đạo hàm để tối ưu hóa các quá trình sản xuất, tính toán năng suất lao động.
Hãy giải quyết các bài tập trên bằng cách sử dụng các công thức đạo hàm cơ bản và sau đó áp dụng kết quả vào các bài toán ứng dụng thực tế.
Lưu ý: Để làm bài tập đạo hàm hiệu quả, học sinh nên nắm vững lý thuyết cơ bản và luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
9.5 Bài tập 5: Tính tích phân
Tính tích phân là một trong những kỹ năng quan trọng trong giải tích. Dưới đây là một bài tập ví dụ và hướng dẫn chi tiết cách tính tích phân của một hàm số.
Bài toán:
Tính tích phân của hàm số sau:
Hướng dẫn giải:
- Áp dụng công thức nguyên hàm:
- \(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\)
- Tính từng thành phần:
- \(\int x^2 \, dx = \frac{x^3}{3}\)
- \(\int 3x \, dx = \frac{3x^2}{2}\)
- \(\int 2 \, dx = 2x\)
- Tổng hợp lại và thay cận:
- \[ \int_{0}^{1} (x^2 + 3x + 2) \, dx = \left[ \frac{x^3}{3} + \frac{3x^2}{2} + 2x \right]_{0}^{1} \]
- Thay cận, ta được kết quả:
- \[ I = \frac{1}{3} + \frac{3}{2} + 2 = \frac{17}{6} \]
Vậy, giá trị của tích phân là \(\frac{17}{6}\).
Bài tập thêm:
- Tính tích phân: \[ I = \int_{0}^{2} \sqrt{4 - x^2} \, dx \] Gợi ý: Sử dụng phương pháp đổi biến.
- Tính tích phân: \[ I = \int_{0}^{1} e^x \cdot (2e^x + 1)^3 \, dx \] Gợi ý: Áp dụng phương pháp tích phân từng phần.
9.6 Bài tập 6: Hệ phương trình tuyến tính
Hệ phương trình tuyến tính là một tập hợp các phương trình tuyến tính mà ta cần tìm giá trị của các biến số sao cho tất cả các phương trình trong hệ đều được thỏa mãn. Một hệ phương trình tuyến tính có thể được viết dưới dạng tổng quát như sau:
Trong đó:
- \(a_1, b_1, c_1, \dots\), \(a_2, b_2, c_2, \dots\), ..., \(a_n, b_n, c_n, \dots\) là các hệ số của các biến.
- \(x, y, z, \dots\) là các biến cần tìm.
- \(d_1, d_2, \dots, d_n\) là các hằng số.
Để giải hệ phương trình tuyến tính, ta có thể sử dụng một trong các phương pháp sau:
- Phương pháp thế: Ta giải một phương trình trong hệ để tìm một biến, sau đó thay giá trị đó vào các phương trình còn lại để tìm các biến khác.
- Phương pháp cộng đại số: Ta cộng hoặc trừ các phương trình trong hệ để loại bỏ một hoặc nhiều biến, từ đó tìm được giá trị của các biến còn lại.
- Phương pháp ma trận: Sử dụng phương pháp đại số tuyến tính với ma trận để giải hệ phương trình.
Ví dụ, giải hệ phương trình sau bằng phương pháp thế:
Bước 1: Giải phương trình thứ hai để tìm \(x\):
Bước 2: Thay \(x = 2y - 3\) vào phương trình đầu tiên:
Bước 3: Giải phương trình trên để tìm \(y\):
Bước 4: Thay giá trị \(y = 2\) vào \(x = 2y - 3\):
Vậy nghiệm của hệ phương trình là \(x = 1\) và \(y = 2\).
9.7 Bài tập 7: Hình học không gian
Trong bài tập này, chúng ta sẽ khám phá một số bài toán cơ bản về hình học không gian, giúp các bạn củng cố kiến thức và nâng cao kỹ năng giải quyết các vấn đề liên quan đến các hình khối ba chiều như hình hộp chữ nhật, hình lăng trụ, hình cầu, và hình chóp.
-
Bài tập 1: Tính thể tích của một hình hộp chữ nhật
Cho một hình hộp chữ nhật có chiều dài \(a = 8 \, \text{cm}\), chiều rộng \(b = 5 \, \text{cm}\), và chiều cao \(c = 10 \, \text{cm}\). Tính thể tích của hình hộp này.
Lời giải:
Thể tích của hình hộp chữ nhật được tính theo công thức:
\[ V = a \times b \times c \]Thay các giá trị vào, ta có:
\[ V = 8 \times 5 \times 10 = 400 \, \text{cm}^3 \]Vậy thể tích của hình hộp chữ nhật là \(400 \, \text{cm}^3\).
-
Bài tập 2: Tính diện tích xung quanh và thể tích của một hình lăng trụ đứng tam giác
Cho hình lăng trụ đứng có đáy là tam giác đều với cạnh đáy bằng \(a = 6 \, \text{cm}\) và chiều cao \(h = 12 \, \text{cm}\). Tính diện tích xung quanh và thể tích của hình lăng trụ.
Lời giải:
Diện tích xung quanh của hình lăng trụ đứng được tính theo công thức:
\[ S_{\text{xq}} = 3a \times h \]Thay các giá trị vào, ta có:
\[ S_{\text{xq}} = 3 \times 6 \times 12 = 216 \, \text{cm}^2 \]Thể tích của hình lăng trụ đứng được tính theo công thức:
\[ V = S_{\text{đáy}} \times h = \frac{\sqrt{3}}{4}a^2 \times h \]Thay các giá trị vào, ta có:
\[ V = \frac{\sqrt{3}}{4} \times 6^2 \times 12 = \frac{\sqrt{3}}{4} \times 36 \times 12 = 108\sqrt{3} \, \text{cm}^3 \]Vậy diện tích xung quanh là \(216 \, \text{cm}^2\) và thể tích của hình lăng trụ đứng là \(108\sqrt{3} \, \text{cm}^3\).
-
Bài tập 3: Tính thể tích của một hình cầu
Cho một hình cầu có bán kính \(r = 4 \, \text{cm}\). Tính thể tích của hình cầu này.
Lời giải:
Thể tích của hình cầu được tính theo công thức:
\[ V = \frac{4}{3}\pi r^3 \]Thay giá trị \(r = 4 \, \text{cm}\) vào, ta có:
\[ V = \frac{4}{3}\pi \times 4^3 = \frac{4}{3}\pi \times 64 = \frac{256}{3}\pi \, \text{cm}^3 \approx 268.08 \, \text{cm}^3 \]Vậy thể tích của hình cầu là khoảng \(268.08 \, \text{cm}^3\).
9.8 Bài tập 8: Xác suất thống kê
Trong bài tập này, chúng ta sẽ áp dụng các kiến thức về xác suất thống kê để giải quyết một số bài toán cụ thể. Hãy cùng thực hiện các bước dưới đây:
-
Xét bài toán sau: Một sân vận động có 10 cửa vào, mỗi cửa có khả năng tiếp nhận trung bình 1000 khán giả trong một giờ. Trong một trận đấu bóng đá của giải Ngoại hạng Anh, sân vận động này dự kiến sẽ đón khoảng 20,000 khán giả. Tính xác suất để có ít nhất một cửa vào tiếp nhận quá tải (hơn 1000 khán giả) trong một giờ.
-
Bước 1: Tính xác suất một cửa vào không bị quá tải. Giả sử số khán giả đến trong một giờ tuân theo phân phối Poisson với trung bình \(\lambda = 2000/10 = 200\).
Chúng ta cần tính xác suất để một cửa tiếp nhận hơn 1000 khán giả:
\[
P(X > 1000) = 1 - P(X \leq 1000)
\]Với \(X\) là số khán giả tại một cửa vào.
-
Bước 2: Tính tổng xác suất các cửa bị quá tải. Giả sử các cửa vào hoạt động độc lập, xác suất tổng quát để ít nhất một cửa bị quá tải sẽ được tính như sau:
\[
P(\text{ít nhất một cửa bị quá tải}) = 1 - \left(P(X \leq 1000)\right)^{10}
\]Trong đó \(P(X \leq 1000)\) là xác suất một cửa không bị quá tải.
-
Bước 3: Sử dụng các bảng phân phối hoặc phần mềm tính toán để xác định giá trị \(P(X \leq 1000)\), sau đó áp dụng vào công thức ở trên để tính xác suất tổng quát.
-
Bước 4: Phân tích kết quả và đưa ra nhận định liệu sân vận động có đủ khả năng đáp ứng được lượng khán giả dự kiến mà không gặp vấn đề quá tải tại các cửa vào hay không.
Hãy thực hiện các bước trên và so sánh kết quả với các điều kiện thực tế trong việc quản lý và tổ chức sự kiện thể thao.
9.9 Bài tập 9: Tính toán ma trận
Trong bài tập này, chúng ta sẽ nghiên cứu cách tính toán ma trận, một công cụ quan trọng trong nhiều lĩnh vực toán học và ứng dụng thực tế. Hãy cùng thực hiện các bước dưới đây để giải quyết bài toán ma trận cụ thể:
-
Cho ma trận \(A\) có kích thước \(2 \times 2\) và ma trận \(B\) có kích thước tương tự như sau:
\[
A = \begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix},
B = \begin{bmatrix}
5 & 6 \\
7 & 8
\end{bmatrix}
\] -
Bước 1: Tính tổng của hai ma trận \(A\) và \(B\). Để cộng hai ma trận, chúng ta chỉ cần cộng từng phần tử tương ứng của hai ma trận:
\[
A + B = \begin{bmatrix}
1+5 & 2+6 \\
3+7 & 4+8
\end{bmatrix}
= \begin{bmatrix}
6 & 8 \\
10 & 12
\end{bmatrix}
\] -
Bước 2: Tính tích của hai ma trận \(A\) và \(B\). Tích của hai ma trận được tính bằng cách nhân từng hàng của ma trận thứ nhất với từng cột của ma trận thứ hai:
\[
A \times B = \begin{bmatrix}
(1*5 + 2*7) & (1*6 + 2*8) \\
(3*5 + 4*7) & (3*6 + 4*8)
\end{bmatrix}
= \begin{bmatrix}
19 & 22 \\
43 & 50
\end{bmatrix}
\] -
Bước 3: Tính định thức của ma trận \(A\). Định thức của ma trận \(2 \times 2\) được tính bằng công thức:
\[
\text{det}(A) = (1*4) - (2*3) = 4 - 6 = -2
\] -
Bước 4: Tính ma trận nghịch đảo của \(A\) (nếu có). Ma trận nghịch đảo \(A^{-1}\) của một ma trận \(2 \times 2\) được tính bằng công thức:
\[
A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix}
4 & -2 \\
-3 & 1
\end{bmatrix}
= \frac{1}{-2} \begin{bmatrix}
4 & -2 \\
-3 & 1
\end{bmatrix}
= \begin{bmatrix}
-2 & 1 \\
1.5 & -0.5
\end{bmatrix}
\]
Hãy thực hiện các bước trên và xác nhận lại kết quả bằng cách áp dụng các tính toán thực tế.

9.10 Bài tập 10: Bất đẳng thức và ứng dụng
Bất đẳng thức là một phần quan trọng trong toán học, đặc biệt là trong việc giải quyết các bài toán tối ưu và phân tích số học. Dưới đây là một số bài tập cụ thể liên quan đến bất đẳng thức và cách ứng dụng chúng trong các bài toán thực tế.
9.10.1 Bài tập 1: Chứng minh bất đẳng thức Cauchy-Schwarz
Cho hai dãy số thực \(a_1, a_2, \ldots, a_n\) và \(b_1, b_2, \ldots, b_n\), chứng minh rằng:
Hướng dẫn: Áp dụng định lý Cauchy-Schwarz cho hai dãy số trên để chứng minh bất đẳng thức này.
9.10.2 Bài tập 2: Ứng dụng bất đẳng thức AM-GM
Chứng minh rằng với mọi số thực dương \(x, y, z\), ta có:
Hướng dẫn: Sử dụng bất đẳng thức trung bình cộng - trung bình nhân (AM-GM) để chứng minh bài toán này.
9.10.3 Bài tập 3: Bất đẳng thức Tam giác
Cho ba điểm \(A\), \(B\) và \(C\) trong không gian, chứng minh rằng:
Hướng dẫn: Sử dụng định lý Tam giác để giải quyết bài toán này và suy luận từ định nghĩa về khoảng cách giữa hai điểm.
9.10.4 Bài tập 4: Ứng dụng trong tối ưu hóa
Giả sử bạn cần tìm giá trị lớn nhất của hàm số \(f(x) = x^2 - 4x + 5\) trên khoảng \(x \geq 0\). Chứng minh rằng:
Hướng dẫn: Sử dụng việc hoàn thành bình phương và bất đẳng thức cơ bản để tìm giá trị nhỏ nhất của hàm số \(f(x)\).
9.10.5 Bài tập 5: Bất đẳng thức giữa trung bình cộng và trung bình cộng của các căn bậc hai
Chứng minh rằng với mọi số thực không âm \(a\) và \(b\), ta có:
Hướng dẫn: Sử dụng bất đẳng thức Jensen hoặc Cauchy-Schwarz để chứng minh điều này.
Trên đây là một số bài tập liên quan đến bất đẳng thức và ứng dụng của chúng trong toán học. Hãy thử giải quyết từng bài để nắm vững hơn về các phương pháp và lý thuyết liên quan.