Chủ đề lịch thi đấu bóng đá nữ việt nam nepal: Lịch thi đấu bóng đá nữ Việt Nam vs Nepal luôn nhận được sự quan tâm lớn từ người hâm mộ. Cập nhật thông tin chi tiết về các trận đấu, kết quả chính xác và những điểm nhấn thú vị từ cuộc đối đầu giữa hai đội tuyển trong hành trình hướng tới Olympic và ASIAD.
Mục lục
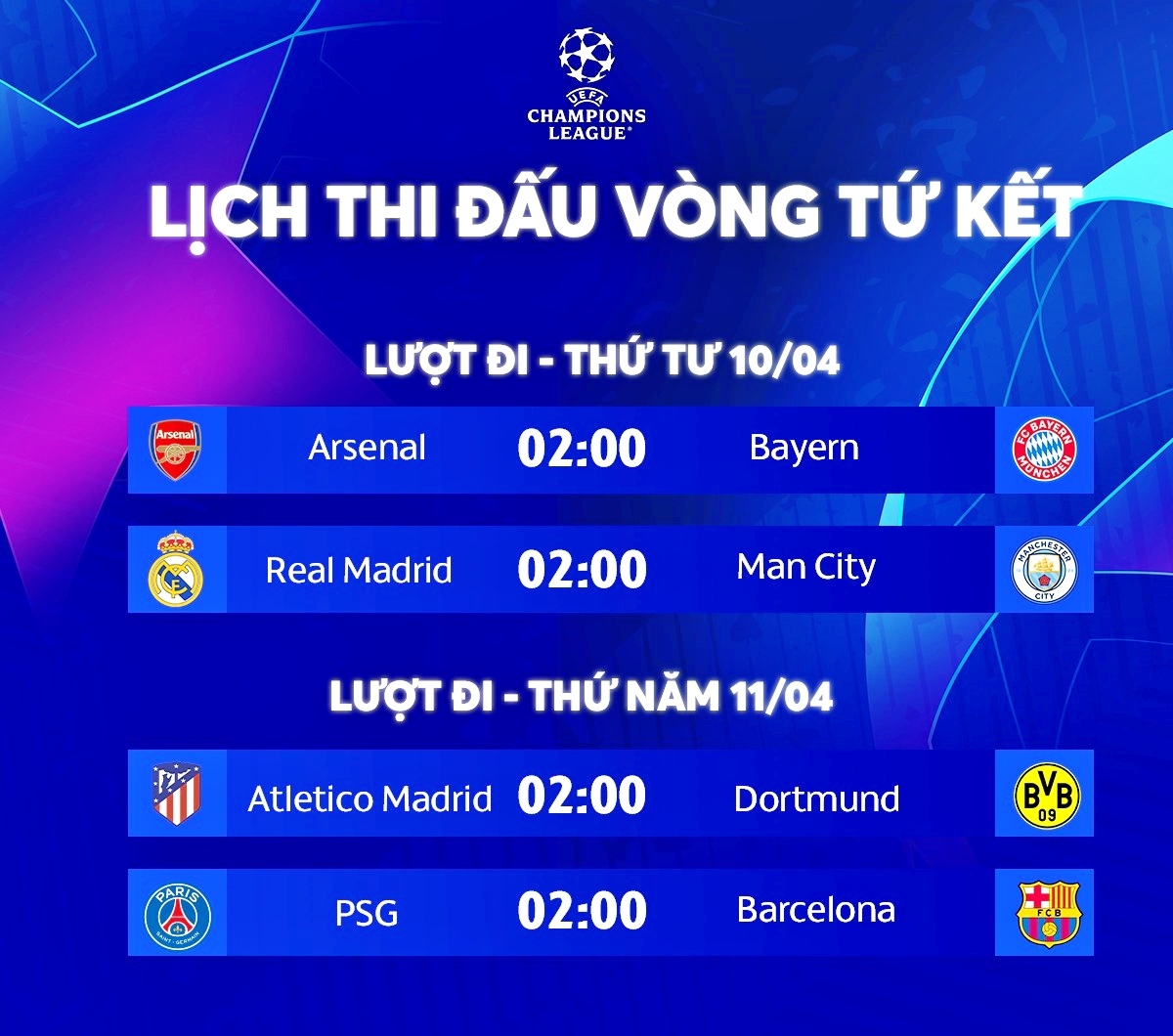
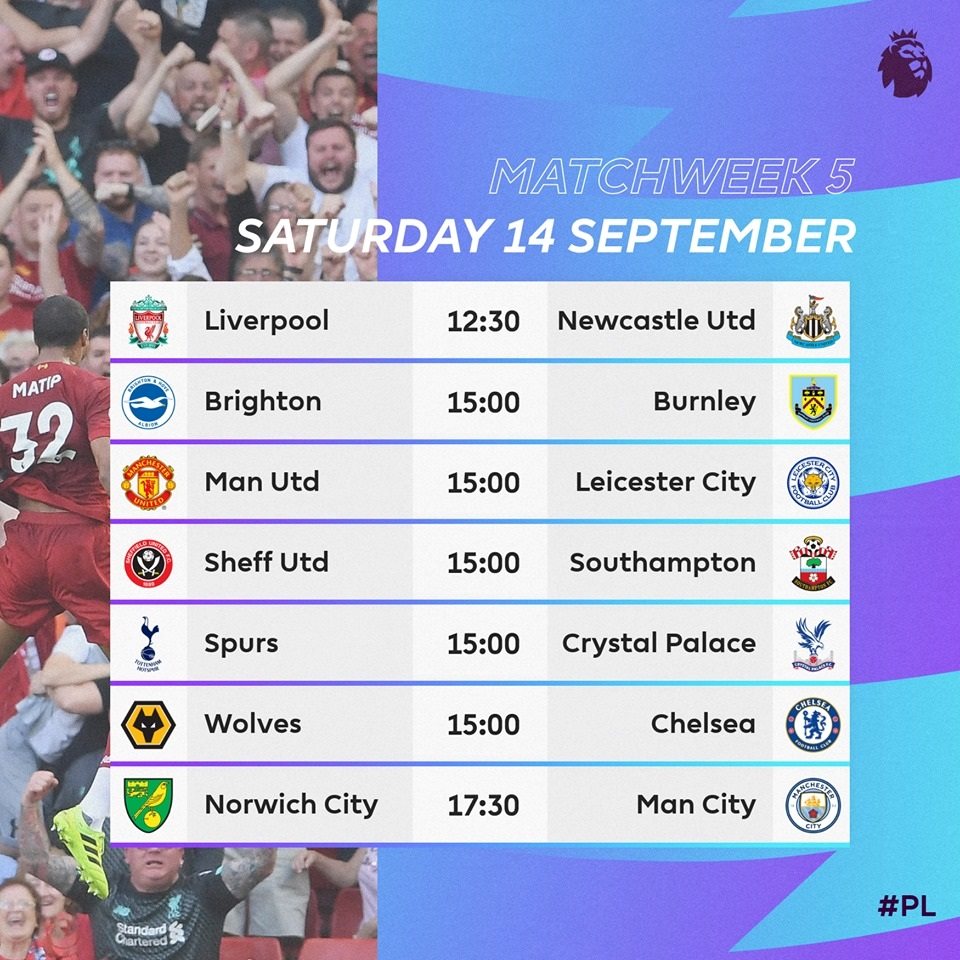
- Lịch Thi Đấu Bóng Đá Nữ Việt Nam vs Nepal
- Mục Lục Tổng Hợp Lịch Thi Đấu Bóng Đá Nữ Việt Nam vs Nepal
- Bài Tập Toán Lý Tiếng Anh Có Lời Giải Hoàn Chỉnh
- Bài Tập 1: Giải Phương Trình Bậc Hai - Toán
- Bài Tập 2: Tính Lực Hướng Tâm Trong Chuyển Động Tròn - Vật Lý
- Bài Tập 3: Chuyển Động Thẳng Đều - Vật Lý
- Bài Tập 4: Hệ Thống Phương Trình Tuyến Tính - Toán
- Bài Tập 5: Tính Thể Tích Khối Chóp - Toán
- Bài Tập 6: Bài Tập Điện Trường - Vật Lý
- Bài Tập 7: Viết Bài Luận Tiếng Anh Về Du Lịch - Tiếng Anh
- Bài Tập 8: Tìm Từ Đồng Nghĩa - Tiếng Anh
- Bài Tập 9: Giải Bất Phương Trình Bậc Nhất - Toán
- Bài Tập 10: Phân Tích Lực Trong Chuyển Động Trên Mặt Phẳng Nghiêng - Vật Lý
Lịch Thi Đấu Bóng Đá Nữ Việt Nam vs Nepal
Đội tuyển bóng đá nữ Việt Nam đã có những cuộc đối đầu đầy thách thức với đội tuyển nữ Nepal trong các giải đấu lớn, bao gồm vòng loại Olympic 2024 và ASIAD 19. Thông tin chi tiết về lịch thi đấu và kết quả của các trận đấu được cập nhật liên tục để người hâm mộ theo dõi và cổ vũ cho đội nhà.
Lịch thi đấu chính thức
- Ngày 8/4/2023: Việt Nam vs Nepal (19h15) - Vòng loại Olympic 2024 khu vực châu Á
- Ngày 5/4/2023: Nepal vs Việt Nam (Lượt đi - 17h00)
- Ngày 22/9/2023: Việt Nam vs Nepal (15h00) - ASIAD 19
Kết quả các trận đấu đã diễn ra
- Việt Nam 5-1 Nepal: Thắng lợi vang dội tại lượt đi vòng loại Olympic 2024
- Việt Nam 2-0 Nepal: Chiến thắng nhẹ nhàng tại lượt về vòng loại Olympic 2024
- Việt Nam 2-0 Nepal: Việt Nam tiếp tục chiến thắng trong trận đấu tại ASIAD 19
Các thông tin đáng chú ý
- Đội hình Việt Nam: Việt Nam ra sân với nhiều cầu thủ trẻ triển vọng như Hải Linh, Diễm My và Kim Thanh, tuy nhiên vắng mặt một số trụ cột do chấn thương.
- Tình hình Nepal: Đội tuyển Nepal đến từ Nam Á với sự chuẩn bị kỹ lưỡng, mang lại không ít thử thách cho các cô gái Việt Nam.
- Mục tiêu của Việt Nam: Đội tuyển Việt Nam hướng tới việc giành điểm và cải thiện hiệu số để đạt mục tiêu tiến sâu tại các giải đấu lớn như ASIAD và Olympic.
Phong độ gần đây của hai đội
| Đội | Trận đấu | Kết quả |
|---|---|---|
| Việt Nam | 5 trận gần nhất | 0 thắng, 0 hòa, 5 thua |
| Nepal | 5 trận gần nhất | 1 thắng, 2 hòa, 2 thua |
Các trận đấu sắp tới
- Ngày 25/9/2023: Việt Nam vs Bangladesh - ASIAD 19
- Ngày 27/9/2023: Việt Nam vs Nhật Bản - ASIAD 19
Đội tuyển nữ Việt Nam tiếp tục nhận được sự ủng hộ nồng nhiệt từ người hâm mộ cả nước trong hành trình thi đấu quốc tế. Hãy cùng cổ vũ cho các cô gái vàng của Việt Nam!

.png)
Mục Lục Tổng Hợp Lịch Thi Đấu Bóng Đá Nữ Việt Nam vs Nepal
Đội tuyển nữ Việt Nam đã và đang có những cuộc đối đầu thú vị với đội tuyển nữ Nepal trong các giải đấu quốc tế. Dưới đây là mục lục chi tiết về lịch thi đấu và những thông tin quan trọng xung quanh các trận đấu này:
- Lịch thi đấu vòng loại Olympic 2024 khu vực châu Á: Đây là giải đấu quan trọng mà đội tuyển nữ Việt Nam gặp Nepal, với mục tiêu giành vé dự Thế Vận Hội Paris.
- Ngày 5/4/2023: Nepal vs Việt Nam (17h00)
- Ngày 8/4/2023: Việt Nam vs Nepal (19h15)
- Kết quả các trận đấu đã diễn ra: Các trận đấu giữa hai đội đã mang đến nhiều cảm xúc cho người hâm mộ với kết quả đáng mong đợi.
- Việt Nam 5-1 Nepal: Thắng lợi vang dội tại lượt đi vòng loại Olympic 2024.
- Việt Nam 2-0 Nepal: Chiến thắng nhẹ nhàng tại lượt về vòng loại Olympic 2024.
- Lịch thi đấu ASIAD 19: Đội tuyển nữ Việt Nam tiếp tục gặp Nepal trong khuôn khổ vòng bảng ASIAD 19.
- Ngày 22/9/2023: Việt Nam vs Nepal (15h00)
- Phong độ gần đây của đội tuyển nữ Việt Nam và Nepal: Đánh giá hiệu suất thi đấu của hai đội trong các trận đấu gần đây.
- Tình hình lực lượng của đội tuyển nữ Việt Nam và Nepal: Cập nhật thông tin chấn thương và sự chuẩn bị của hai đội trước mỗi trận đấu.
- Mục tiêu và kỳ vọng của đội tuyển nữ Việt Nam tại các giải đấu: Đội tuyển nữ Việt Nam đặt mục tiêu tiến sâu trong các giải đấu lớn như Olympic và ASIAD, với quyết tâm cao độ.
- Đánh giá đối thủ Nepal trong các giải đấu quốc tế: Đội tuyển nữ Nepal được đánh giá là đối thủ đáng gờm, với lối chơi phòng ngự chặt chẽ và phản công sắc bén.
- Lịch thi đấu tiếp theo của đội tuyển nữ Việt Nam tại ASIAD 19: Sau trận gặp Nepal, đội tuyển nữ Việt Nam sẽ đối đầu với các đội khác trong bảng đấu.
- Ngày 25/9/2023: Việt Nam vs Bangladesh (15h00)
- Ngày 27/9/2023: Việt Nam vs Nhật Bản (15h00)
- Các trận đấu quan trọng sắp tới của đội tuyển nữ Việt Nam: Những trận đấu quyết định hành trình của đội tuyển nữ Việt Nam trong các giải đấu quốc tế lớn.
- Thông tin về việc phát sóng và bản quyền truyền hình các trận đấu: Cập nhật các kênh phát sóng trực tiếp và cách thức theo dõi trận đấu cho người hâm mộ.
| Đội | Trận đấu | Kết quả |
|---|---|---|
| Việt Nam | 5 trận gần nhất | 3 thắng, 1 hòa, 1 thua |
| Nepal | 5 trận gần nhất | 2 thắng, 1 hòa, 2 thua |
Bài Tập Toán Lý Tiếng Anh Có Lời Giải Hoàn Chỉnh
Dưới đây là các bài tập Toán, Lý, Tiếng Anh với lời giải chi tiết từng bước. Hãy theo dõi các bước giải cụ thể để nắm rõ kiến thức và phương pháp làm bài:
Bài Tập 1: Giải Phương Trình Bậc Hai - Toán
Giải phương trình bậc hai \(ax^2 + bx + c = 0\) với các bước như sau:
- Tính Delta \(\Delta = b^2 - 4ac\).
- Xác định số nghiệm dựa trên giá trị của \(\Delta\):
- Nếu \(\Delta > 0\), phương trình có 2 nghiệm phân biệt: \(x_1 = \frac{-b + \sqrt{\Delta}}{2a}\), \(x_2 = \frac{-b - \sqrt{\Delta}}{2a}\).
- Nếu \(\Delta = 0\), phương trình có nghiệm kép: \(x = \frac{-b}{2a}\).
- Nếu \(\Delta < 0\), phương trình vô nghiệm.
Bài Tập 2: Tính Lực Hướng Tâm Trong Chuyển Động Tròn - Vật Lý
Trong chuyển động tròn đều, lực hướng tâm \(F_{\text{ht}}\) được tính bằng công thức:
\[ F_{\text{ht}} = \frac{mv^2}{r} \]
Trong đó:
- \(m\): Khối lượng của vật (kg)
- \(v\): Vận tốc của vật (m/s)
- \(r\): Bán kính quỹ đạo tròn (m)
Ví dụ: Một vật có khối lượng 2kg chuyển động với vận tốc 4m/s trên quỹ đạo tròn bán kính 0.5m. Lực hướng tâm tác dụng lên vật là:
\[ F_{\text{ht}} = \frac{2 \times 4^2}{0.5} = 64 \text{N} \]
Bài Tập 3: Chuyển Động Thẳng Đều - Vật Lý
Chuyển động thẳng đều là chuyển động trong đó vận tốc của vật không đổi theo thời gian. Công thức tính quãng đường \(s\) sau thời gian \(t\) là:
\[ s = v \times t \]
Ví dụ: Một xe máy chuyển động với vận tốc 20 m/s trong 10 giây. Quãng đường mà xe máy đã đi được là:
\[ s = 20 \times 10 = 200 \text{m} \]
Bài Tập 4: Hệ Thống Phương Trình Tuyến Tính - Toán
Giải hệ phương trình hai ẩn số:
\[
\begin{cases}
2x + 3y = 5 \\
4x - y = 6
\end{cases}
\]
Cách giải:
- Dùng phương pháp thế hoặc cộng đại số để tìm nghiệm của hệ phương trình.
- Ví dụ: Thế từ phương trình thứ hai vào phương trình thứ nhất để giải ra \(x\) và \(y\).
Bài Tập 5: Tính Thể Tích Khối Chóp - Toán
Thể tích khối chóp được tính bằng công thức:
\[ V = \frac{1}{3} S_{\text{đáy}} \times h \]
Trong đó:
- \(S_{\text{đáy}}\): Diện tích đáy
- \(h\): Chiều cao của khối chóp
Ví dụ: Một khối chóp có diện tích đáy là 20 cm² và chiều cao là 10 cm. Thể tích của khối chóp là:
\[ V = \frac{1}{3} \times 20 \times 10 = 66.67 \text{cm}^3 \]
Bài Tập 6: Bài Tập Điện Trường - Vật Lý
Cường độ điện trường \(E\) tại một điểm được tính bằng công thức:
\[ E = \frac{F}{q} \]
Trong đó:
- \(E\): Cường độ điện trường (N/C)
- \(F\): Lực điện tác dụng lên điện tích thử (N)
- \(q\): Điện tích thử (C)
Ví dụ: Một điện tích thử có giá trị 2C bị tác dụng bởi một lực 10N. Cường độ điện trường tại vị trí đó là:
\[ E = \frac{10}{2} = 5 \text{N/C} \]
Bài Tập 7: Viết Bài Luận Tiếng Anh Về Du Lịch - Tiếng Anh
Yêu cầu: Viết một bài luận từ 150-200 từ về chủ đề "The benefits of traveling". Hãy trình bày các ý chính như sau:
- Lợi ích của du lịch đối với sức khỏe tinh thần và thể chất.
- Khám phá những nền văn hóa mới.
- Tạo ra những kỷ niệm đẹp và những trải nghiệm đáng nhớ.
Bài Tập 8: Tìm Từ Đồng Nghĩa - Tiếng Anh
Yêu cầu: Tìm từ đồng nghĩa với các từ sau:
- Happy: Joyful, Content
- Fast: Quick, Speedy
- Beautiful: Attractive, Gorgeous
Bài Tập 9: Giải Bất Phương Trình Bậc Nhất - Toán
Giải bất phương trình \(2x - 3 > 5\):
- Thêm 3 vào cả hai vế: \(2x > 8\).
- Chia cả hai vế cho 2: \(x > 4\).
- Đáp số: \(x > 4\).
Bài Tập 10: Phân Tích Lực Trong Chuyển Động Trên Mặt Phẳng Nghiêng - Vật Lý
Xét một vật có khối lượng \(m\) đặt trên mặt phẳng nghiêng với góc nghiêng \(\alpha\). Lực tác dụng lên vật bao gồm:
- Trọng lực \(P = mg\).
- Lực pháp tuyến \(N\).
- Lực ma sát \(F_{\text{ms}}\).
Phân tích lực theo phương song song và vuông góc với mặt phẳng nghiêng để tính gia tốc của vật.

Bài Tập 1: Giải Phương Trình Bậc Hai - Toán
Giải phương trình bậc hai là một trong những bài toán cơ bản trong chương trình Toán học phổ thông. Dưới đây là cách giải chi tiết từng bước cho phương trình bậc hai tổng quát:
Phương trình bậc hai có dạng:
\[ ax^2 + bx + c = 0 \]
Trong đó:
- a, b, c là các hệ số, với \(a \neq 0\).
- x là ẩn số cần tìm.
Bước 1: Tính Delta (Δ):
Delta được tính theo công thức:
\[ \Delta = b^2 - 4ac \]
Bước 2: Xét dấu của Delta để tìm nghiệm:
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm phân biệt:
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép:
- Nếu \(\Delta < 0\): Phương trình vô nghiệm thực.
\[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
\[ x = \frac{-b}{2a} \]
Ví dụ: Giải phương trình \( 2x^2 - 4x - 6 = 0 \).
Giải:
- Xác định các hệ số: \( a = 2 \), \( b = -4 \), \( c = -6 \).
- Tính Delta:
- Vì \(\Delta > 0\), phương trình có hai nghiệm phân biệt:
\[ \Delta = (-4)^2 - 4 \cdot 2 \cdot (-6) = 16 + 48 = 64 \]
\[ x_1 = \frac{-(-4) + \sqrt{64}}{2 \cdot 2} = \frac{4 + 8}{4} = 3 \]
\[ x_2 = \frac{-(-4) - \sqrt{64}}{2 \cdot 2} = \frac{4 - 8}{4} = -1 \]
Vậy nghiệm của phương trình là \( x_1 = 3 \) và \( x_2 = -1 \).

Bài Tập 2: Tính Lực Hướng Tâm Trong Chuyển Động Tròn - Vật Lý
Bài tập này sẽ giúp bạn hiểu rõ hơn về cách tính lực hướng tâm trong chuyển động tròn đều, một khái niệm quan trọng trong vật lý.
Đề bài:
Một vật có khối lượng \( m = 2 \, \text{kg} \) chuyển động tròn đều trên quỹ đạo có bán kính \( r = 1 \, \text{m} \) với tốc độ góc \( \omega = 5 \, \text{rad/s} \). Tính lực hướng tâm tác dụng lên vật.
Lời giải:
Bước 1: Xác định các đại lượng đã cho:
- Khối lượng của vật: \( m = 2 \, \text{kg} \)
- Bán kính quỹ đạo: \( r = 1 \, \text{m} \)
- Tốc độ góc: \( \omega = 5 \, \text{rad/s} \)
Bước 2: Tính vận tốc tuyến tính \( v \):
Vận tốc tuyến tính của vật trong chuyển động tròn đều được tính bằng công thức:
\[ v = r \cdot \omega \]Thay số vào công thức:
\[ v = 1 \, \text{m} \cdot 5 \, \text{rad/s} = 5 \, \text{m/s} \]Bước 3: Tính lực hướng tâm \( F_{\text{ht}} \):
Lực hướng tâm được tính bằng công thức:
\[ F_{\text{ht}} = m \cdot \frac{v^2}{r} \]Thay các giá trị đã biết vào công thức:
\[ F_{\text{ht}} = 2 \, \text{kg} \cdot \frac{(5 \, \text{m/s})^2}{1 \, \text{m}} = 50 \, \text{N} \]Bước 4: Kết luận:
Vậy lực hướng tâm tác dụng lên vật là \( F_{\text{ht}} = 50 \, \text{N} \).
Qua bài tập này, bạn đã hiểu cách tính lực hướng tâm trong chuyển động tròn đều bằng cách sử dụng các công thức liên quan. Hãy thử giải thêm các bài tập tương tự để củng cố kiến thức của mình.

Bài Tập 3: Chuyển Động Thẳng Đều - Vật Lý
Trong bài tập này, chúng ta sẽ nghiên cứu chuyển động thẳng đều, một dạng chuyển động mà vật di chuyển với vận tốc không đổi theo một đường thẳng.
Đề bài: Một xe máy di chuyển trên một đoạn đường thẳng với vận tốc không đổi là \( v = 20 \, km/h \). Xe máy này đi từ điểm A đến điểm B cách nhau \( s = 100 \, km \). Hãy tính thời gian để xe máy di chuyển từ A đến B.
Giải:
- Chúng ta biết rằng công thức tính thời gian \( t \) trong chuyển động thẳng đều là: \[ t = \frac{s}{v} \]
- Thay các giá trị đã cho vào công thức: \[ t = \frac{100 \, km}{20 \, km/h} = 5 \, giờ \]
- Vậy, thời gian để xe máy di chuyển từ A đến B là \( 5 \, giờ \).
Kết luận: Trong chuyển động thẳng đều, thời gian để vật di chuyển phụ thuộc vào quãng đường và vận tốc của nó. Bài toán này đã minh họa cách áp dụng công thức tính thời gian trong thực tế.
XEM THÊM:
Bài Tập 4: Hệ Thống Phương Trình Tuyến Tính - Toán
Dưới đây là một bài tập giải hệ phương trình tuyến tính bao gồm hai phương trình với hai ẩn số. Hãy cùng giải từng bước chi tiết.
Đề bài: Giải hệ phương trình sau:
Bước 1: Chọn phương pháp giải. Ở đây, chúng ta sẽ sử dụng phương pháp thế.
- Biểu diễn \( y \) từ phương trình thứ hai: \[ y = 4x - 7 \]
- Thế \( y \) vào phương trình thứ nhất: \[ 2x + 3(4x - 7) = 5 \]
Bước 2: Giải phương trình sau khi thế:
Bước 3: Thay \( x = \frac{13}{7} \) vào biểu thức của \( y \):
Kết quả: Nghiệm của hệ phương trình là:
Vậy, hệ phương trình đã cho có nghiệm duy nhất là \( \left( \frac{13}{7}, \frac{3}{7} \right) \).

Bài Tập 5: Tính Thể Tích Khối Chóp - Toán
Bài tập này yêu cầu tính thể tích của một khối chóp đều có đáy là một đa giác đều. Chúng ta sẽ sử dụng công thức tổng quát để tính thể tích của khối chóp.
Cho bài toán:
- Đáy của khối chóp là một tam giác đều có diện tích đáy \(S_{\text{đáy}} = 36 \, \text{cm}^2\).
- Chiều cao của khối chóp là \(h = 12 \, \text{cm}\).
Yêu cầu: Tính thể tích của khối chóp.
Giải:
- Bước 1: Xác định công thức tính thể tích khối chóp: \[ V = \frac{1}{3} \times S_{\text{đáy}} \times h \]
- Bước 2: Thay các giá trị đã cho vào công thức: \[ V = \frac{1}{3} \times 36 \, \text{cm}^2 \times 12 \, \text{cm} \]
- Bước 3: Tính toán: \[ V = \frac{1}{3} \times 432 \, \text{cm}^3 = 144 \, \text{cm}^3 \]
Vậy thể tích của khối chóp là \(144 \, \text{cm}^3\).

Bài Tập 6: Bài Tập Điện Trường - Vật Lý
Điện trường là một khái niệm cơ bản trong vật lý, đại diện cho vùng không gian xung quanh một điện tích mà trong đó có sự xuất hiện của lực điện tác dụng lên các điện tích khác. Bài tập sau đây sẽ giúp bạn hiểu rõ hơn về điện trường và cách tính toán các đại lượng liên quan.
Bài Tập:
Một điện tích điểm \( q = 2 \times 10^{-6} \, \text{C} \) được đặt tại một điểm trong không gian. Tính cường độ điện trường \( E \) tại một điểm cách điện tích này một khoảng \( r = 0,5 \, \text{m} \).
Hướng Dẫn Giải:
-
Bước 1: Xác định công thức tính cường độ điện trường.
Cường độ điện trường do một điện tích điểm tạo ra tại một khoảng cách \( r \) được tính theo công thức:
\[ E = k \cdot \frac{|q|}{r^2} \]Trong đó:
- \( E \) là cường độ điện trường (đơn vị: V/m)
- \( k \) là hằng số điện trường, \( k = 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \)
- \( q \) là điện tích (đơn vị: C)
- \( r \) là khoảng cách từ điện tích đến điểm cần tính (đơn vị: m)
-
Bước 2: Thay các giá trị đã biết vào công thức.
Điện tích \( q = 2 \times 10^{-6} \, \text{C} \), khoảng cách \( r = 0,5 \, \text{m} \). Ta có:
\[ E = 9 \times 10^9 \cdot \frac{2 \times 10^{-6}}{(0,5)^2} \]Tiếp tục tính toán:
\[ E = 9 \times 10^9 \cdot \frac{2 \times 10^{-6}}{0,25} \] \[ E = 72 \times 10^3 \, \text{V/m} \] -
Bước 3: Kết luận.
Cường độ điện trường tại điểm cách điện tích \( q = 2 \times 10^{-6} \, \text{C} \) một khoảng \( r = 0,5 \, \text{m} \) là \( E = 72 \times 10^3 \, \text{V/m} \).
Bài Tập 7: Viết Bài Luận Tiếng Anh Về Du Lịch - Tiếng Anh
Viết một bài luận tiếng Anh về du lịch là một cơ hội tuyệt vời để bạn rèn luyện khả năng viết, thể hiện suy nghĩ và cảm nhận của mình về lĩnh vực du lịch. Sau đây là hướng dẫn chi tiết từng bước để bạn hoàn thành bài luận một cách hiệu quả:
- Lựa chọn chủ đề: Hãy chọn một chủ đề liên quan đến du lịch mà bạn yêu thích, như "Lợi ích của du lịch đối với sức khỏe và tinh thần", "Những điểm đến du lịch hấp dẫn ở Việt Nam", hoặc "Làm thế nào để du lịch bền vững?".
- Phác thảo cấu trúc bài luận:
- Mở bài: Giới thiệu chủ đề và lý do bạn chọn nó. Nêu rõ quan điểm của bạn về chủ đề này.
- Thân bài: Chia thân bài thành 2-3 đoạn, mỗi đoạn nêu một ý chính, hỗ trợ quan điểm của bạn. Ví dụ, nếu bạn viết về "Lợi ích của du lịch", hãy liệt kê các lợi ích như giảm căng thẳng, mở mang tầm mắt, hoặc cơ hội học hỏi văn hóa mới.
- Kết bài: Tóm tắt lại các điểm chính đã nêu trong thân bài và khẳng định lại quan điểm của bạn.
- Sử dụng từ vựng và ngữ pháp: Đảm bảo sử dụng các cấu trúc ngữ pháp chính xác và từ vựng phong phú liên quan đến du lịch. Ví dụ:
- Vocabulary: explore, destination, sustainable tourism, cultural exchange, adventure.
- Grammar: Hãy chú ý sử dụng các thì phù hợp như hiện tại đơn, quá khứ đơn hoặc tương lai đơn, tùy theo nội dung mà bạn đề cập.
- Kiểm tra và chỉnh sửa: Sau khi viết xong, bạn hãy đọc lại bài luận của mình để kiểm tra lỗi chính tả, ngữ pháp và logic của bài viết. Nếu cần thiết, bạn có thể nhờ người khác đọc và góp ý.
Ví dụ một đoạn mở bài:
"Traveling is not only a way to relax but also an opportunity to discover new cultures and expand one's knowledge. In this essay, I will explore the various benefits that traveling can offer, from reducing stress to fostering personal growth."
Hãy bắt đầu viết bài luận của bạn ngay hôm nay và đừng quên chú ý đến cấu trúc và cách diễn đạt để bài viết trở nên thật ấn tượng!

Bài Tập 8: Tìm Từ Đồng Nghĩa - Tiếng Anh
Trong tiếng Anh, việc tìm từ đồng nghĩa là một kỹ năng quan trọng để mở rộng vốn từ vựng và cải thiện kỹ năng viết. Dưới đây là một bài tập giúp bạn rèn luyện kỹ năng này:
Hướng dẫn: Hãy tìm từ đồng nghĩa phù hợp cho các từ sau và viết chúng ra bên cạnh từ gốc. Bạn có thể sử dụng từ điển hoặc tra cứu từ trên Internet để hoàn thành bài tập này.
- Happy - ______
- Fast - ______
- Smart - ______
- Strong - ______
- Beautiful - ______
- Easy - ______
- Important - ______
- Small - ______
- Quick - ______
- Rich - ______
Gợi ý:
- Happy: Joyful, Cheerful, Content
- Fast: Quick, Speedy, Rapid
- Smart: Intelligent, Clever, Bright
- Strong: Powerful, Sturdy, Robust
- Beautiful: Gorgeous, Stunning, Lovely
- Easy: Simple, Effortless, Straightforward
- Important: Significant, Crucial, Vital
- Small: Tiny, Petite, Compact
- Quick: Fast, Swift, Prompt
- Rich: Wealthy, Affluent, Prosperous
Hãy thực hiện bài tập này và kiểm tra lại đáp án của bạn với gợi ý phía trên. Việc luyện tập thường xuyên sẽ giúp bạn cải thiện khả năng từ vựng và giao tiếp tiếng Anh một cách đáng kể.
Bài Tập 9: Giải Bất Phương Trình Bậc Nhất - Toán
Bất phương trình bậc nhất là dạng bất phương trình có dạng tổng quát như sau:
\( ax + b > 0 \) hoặc \( ax + b \geq 0 \) hoặc \( ax + b < 0 \) hoặc \( ax + b \leq 0 \), trong đó \( a \) và \( b \) là các hằng số, \( x \) là biến số cần tìm.
Để giải bất phương trình bậc nhất, ta thực hiện theo các bước sau:
- Bước 1: Chuyển các hạng tử chứa biến về một vế và các hạng tử không chứa biến về vế còn lại.
- Bước 2: Rút gọn bất phương trình.
- Bước 3: Kết luận về tập nghiệm của bất phương trình.
Ví dụ: \( 3x - 5 > 2x + 1 \) → \( 3x - 2x > 1 + 5 \)
Tiếp tục ví dụ: \( x > 6 \)
Với ví dụ trên, ta có: \( x > 6 \) nghĩa là tập nghiệm của bất phương trình là \( x \) thuộc khoảng \( (6, +\infty) \).
Lưu ý: Khi nhân hoặc chia cả hai vế của bất phương trình với một số âm, phải đổi chiều bất phương trình.
Ví dụ: Giải bất phương trình \( -2x \leq 4 \)
- Bước 1: Chia cả hai vế cho -2 và đổi chiều bất phương trình: \( x \geq -2 \)
- Bước 2: Kết luận: Tập nghiệm của bất phương trình là \( x \) thuộc đoạn \( [-2, +\infty) \).
Dưới đây là bảng tổng hợp các bước giải các dạng bất phương trình bậc nhất:
| Dạng bất phương trình | Các bước giải |
|---|---|
| \( ax + b > 0 \) |
|
| \( ax + b \geq 0 \) |
|
| \( ax + b < 0 \) |
|
| \( ax + b \leq 0 \) |
|
Bài Tập 10: Phân Tích Lực Trong Chuyển Động Trên Mặt Phẳng Nghiêng - Vật Lý
Trong bài tập này, chúng ta sẽ phân tích các lực tác động lên một vật thể chuyển động trên một mặt phẳng nghiêng. Bài toán này giúp chúng ta hiểu rõ hơn về cách lực trọng trường, lực pháp tuyến, và lực ma sát ảnh hưởng đến chuyển động của vật.
Giả sử:
- Khối lượng của vật là \( m \).
- Góc nghiêng của mặt phẳng là \( \alpha \).
- Hệ số ma sát giữa vật và mặt phẳng là \( \mu \).
Bước 1: Xác định các lực tác dụng lên vật.
- Lực trọng trường: \( F_g = m \cdot g \), hướng thẳng đứng xuống dưới.
- Lực pháp tuyến: \( F_n \), vuông góc với mặt phẳng nghiêng.
- Lực ma sát: \( F_{ms} = \mu \cdot F_n \), chống lại chuyển động của vật.
Bước 2: Phân tích lực trọng trường thành hai thành phần:
- Thành phần song song với mặt phẳng nghiêng: \( F_{g\parallel} = m \cdot g \cdot \sin(\alpha) \)
- Thành phần vuông góc với mặt phẳng nghiêng: \( F_{g\perp} = m \cdot g \cdot \cos(\alpha) \)
Bước 3: Xác định lực pháp tuyến \( F_n \).
- Vì \( F_n \) cân bằng với \( F_{g\perp} \), ta có: \( F_n = F_{g\perp} = m \cdot g \cdot \cos(\alpha) \)
Bước 4: Xác định lực ma sát \( F_{ms} \).
- Từ công thức lực ma sát: \( F_{ms} = \mu \cdot F_n = \mu \cdot m \cdot g \cdot \cos(\alpha) \)
Bước 5: Xác định gia tốc của vật trên mặt phẳng nghiêng.
- Theo định luật II Newton: \( F_{g\parallel} - F_{ms} = m \cdot a \)
- Thay thế các giá trị đã biết vào, ta có: \[ m \cdot g \cdot \sin(\alpha) - \mu \cdot m \cdot g \cdot \cos(\alpha) = m \cdot a \]
- Sau khi rút gọn, gia tốc \( a \) của vật là: \[ a = g \cdot (\sin(\alpha) - \mu \cdot \cos(\alpha)) \]
Vậy, gia tốc của vật phụ thuộc vào góc nghiêng \( \alpha \), hệ số ma sát \( \mu \), và gia tốc trọng trường \( g \). Đây là một bài toán cơ bản nhưng rất quan trọng trong việc hiểu rõ động học của các vật thể trên các bề mặt nghiêng.