Lịch Thi Đấu Bóng Đá Việt Nam Chung Kết: Cập Nhật Mới Nhất Và Dự Đoán Kết Quả

Thông tin về lịch thi đấu bóng đá của Việt Nam tại các vòng chung kết được cập nhật thường xuyên trên các trang báo điện tử và nền tảng thể thao. Dưới đây là tổng hợp chi tiết các thông tin liên quan đến lịch thi đấu các trận chung kết mà đội tuyển Việt Nam tham gia.

Lịch thi đấu vòng chung kết AFF Cup

• Trận đấu: Việt Nam vs Thái Lan
• Thời gian: 19h00 ngày 22/12/2023
• Địa điểm: Sân vận động Mỹ Đình, Hà Nội

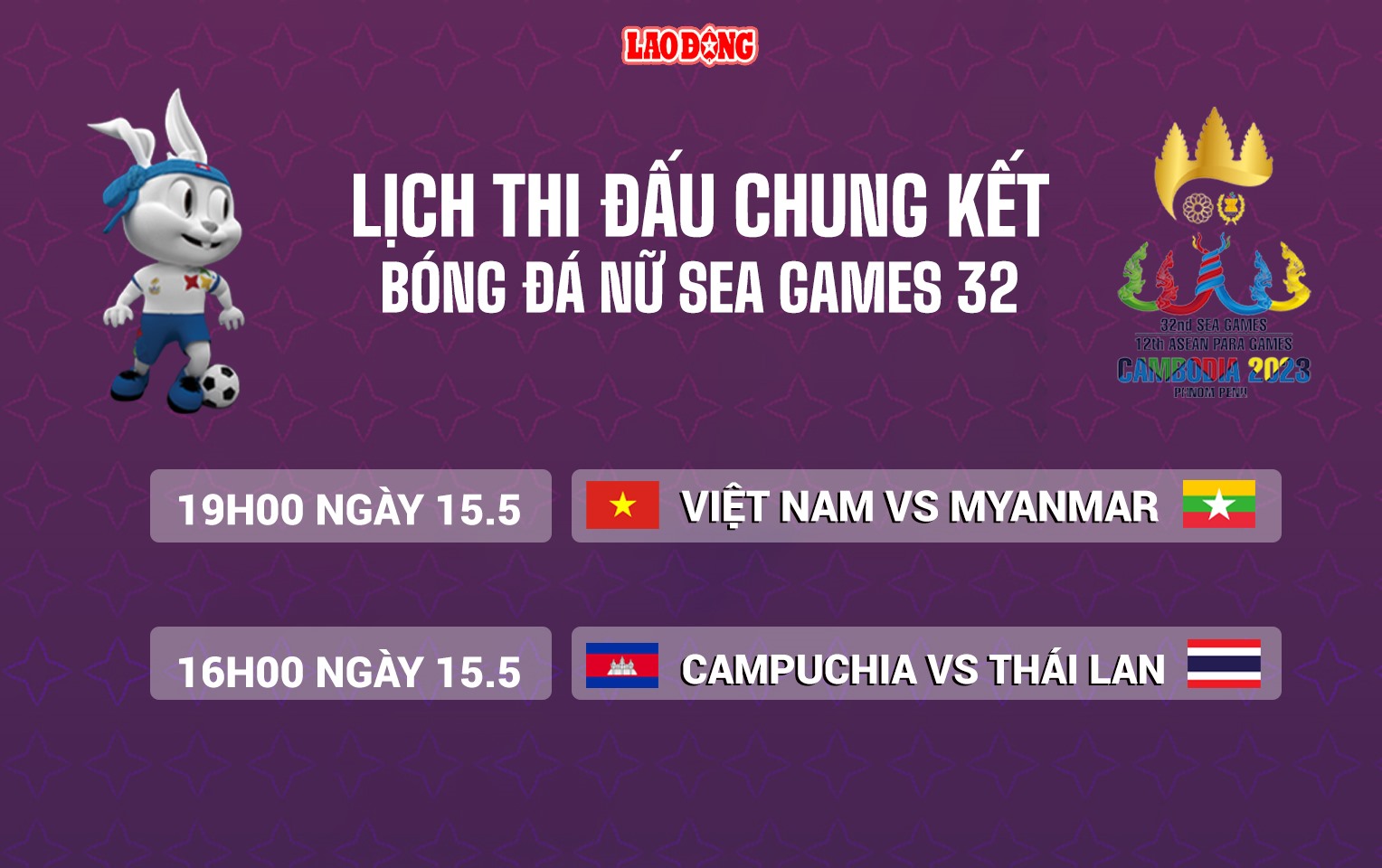
Lịch thi đấu vòng chung kết SEA Games

• Trận đấu: U23 Việt Nam vs U23 Thái Lan
• Thời gian: 19h00 ngày 22/5/2024
• Phát sóng: VTV6, VTVGo, YouTube VTV Thể Thao

Lịch thi đấu vòng chung kết Asian Cup

• Giải đấu: Vòng chung kết Asian Cup 2023
• Trận đấu: Việt Nam vs Nhật Bản
• Thời gian: 20h00 ngày 15/1/2024
• Địa điểm: Sân vận động quốc gia Bukit Jalil, Malaysia
• Phát sóng: VTV2, VTVGo

Thành tích gần đây của đội tuyển Việt Nam

• Vô địch AFF Cup 2018, 2022
• Huy chương Vàng SEA Games 31, 32
• Vòng 1/8 Asian Cup 2019

Những cầu thủ đáng chú ý

• Nguyễn Quang Hải: Tiền vệ kiến thiết, đã ghi nhiều bàn thắng quan trọng cho đội tuyển Việt Nam.
• Nguyễn Tiến Linh: Tiền đạo chủ lực với khả năng dứt điểm ấn tượng.
• Đỗ Duy Mạnh: Hậu vệ với khả năng phòng ngự chắc chắn và không chiến tốt.

Nhận định trước trận đấu

Đội tuyển Việt Nam được đánh giá cao về khả năng chiến thắng trong các trận chung kết sắp tới nhờ vào phong độ ổn định và sự đoàn kết trong lối chơi. Các đối thủ như Thái Lan và Nhật Bản đều mạnh, nhưng với sự chuẩn bị kỹ lưỡng, đội tuyển Việt Nam hoàn toàn có thể tạo nên bất ngờ.

• Lịch Thi Đấu Bóng Đá Việt Nam Chung Kết 2024
  • Lịch thi đấu các trận chung kết bóng đá Việt Nam 2024 tại AFF Cup, SEA Games và Asian Cup.
  • Thông tin thời gian, địa điểm, và kênh phát sóng trực tiếp các trận đấu.
  • Những trận đấu quyết định ngôi vô địch và cơ hội của đội tuyển Việt Nam.
• Kết Quả Chung Kết Và Phân Tích Trận Đấu
  • Tổng hợp kết quả các trận chung kết bóng đá Việt Nam.
  • Phân tích chiến thuật, lối chơi và những điểm nhấn quan trọng trong các trận đấu.
  • Nhận định từ các chuyên gia và huấn luyện viên sau trận đấu.
• Những Cầu Thủ Nổi Bật Trong Chung Kết
  • Danh sách các cầu thủ xuất sắc nhất trong các trận chung kết của đội tuyển Việt Nam.
  • Vai trò và tầm ảnh hưởng của từng cầu thủ trong đội hình.
  • Những khoảnh khắc ấn tượng và những bàn thắng quyết định trong trận đấu.
• Lịch Thi Đấu Dự Kiến Và Đối Thủ Tiềm Năng
  • Lịch thi đấu dự kiến cho các giải đấu quốc tế trong tương lai mà đội tuyển Việt Nam có thể tham gia.
  • Phân tích đối thủ tiềm năng và những thách thức mà đội tuyển có thể gặp phải.
  • Những chiến lược mà đội tuyển Việt Nam cần chuẩn bị để đối phó với các đối thủ mạnh.
• Thành Tích Chung Kết Trong Lịch Sử
  • Thành tích của đội tuyển Việt Nam trong các trận chung kết quốc tế trước đây.
  • Những chiến thắng lịch sử và bài học từ các trận thua.
  • Sự phát triển và tiến bộ của bóng đá Việt Nam qua từng giai đoạn.
• Nhận Định Và Dự Đoán Trước Chung Kết
  • Nhận định về cơ hội vô địch của đội tuyển Việt Nam từ các chuyên gia.
  • Dự đoán tỉ số và kịch bản của trận chung kết.
  • Yếu tố tâm lý và thể lực ảnh hưởng đến kết quả trận đấu.

• Bài Tập 1: Tính Tỉ Số Bàn Thắng

  Giả sử đội tuyển Việt Nam ghi được \(n\) bàn trong trận chung kết, và đối thủ ghi được \(m\) bàn. Tính tỉ số bàn thắng của trận đấu.

  Lời giải: Tỉ số bàn thắng là \(\frac{n}{m}\). Nếu \(n > m\), Việt Nam thắng; nếu \(n < m\), đối thủ thắng; nếu \(n = m\), trận đấu hòa.

• Bài Tập 2: Tính Xác Suất Thắng Của Đội Tuyển Việt Nam

  Cho rằng xác suất Việt Nam thắng trận chung kết là \(P(V)\), xác suất đối thủ thắng là \(P(O)\), và xác suất hòa là \(P(H)\). Biết rằng tổng xác suất là 1, hãy tính \(P(V)\) khi biết \(P(O)\) và \(P(H)\).

  Lời giải: \(P(V) = 1 - (P(O) + P(H))\)

• Bài Tập 3: Tính Tổng Số Bàn Thắng Trong Giải Đấu

  Cho rằng trong giải đấu, đội tuyển Việt Nam ghi được \(a\) bàn trong mỗi trận và đã chơi \(b\) trận. Tính tổng số bàn thắng mà đội tuyển Việt Nam đã ghi trong toàn bộ giải đấu.

  Lời giải: Tổng số bàn thắng là \(a \times b\).

• Bài Tập 4: Tính Khoảng Cách Chạy Của Cầu Thủ

  Giả sử một cầu thủ chạy \(x\) km trong hiệp 1 và \(y\) km trong hiệp 2 của trận chung kết. Tính tổng khoảng cách mà cầu thủ này đã chạy trong cả trận đấu.

  Lời giải: Tổng khoảng cách chạy là \(x + y\) km.

• Bài Tập 5: Tính Hiệu Số Bàn Thắng

  Đội tuyển Việt Nam ghi được \(p\) bàn trong trận chung kết, và đối thủ ghi được \(q\) bàn. Tính hiệu số bàn thắng của trận đấu.

  Lời giải: Hiệu số bàn thắng là \(p - q\).

• Bài Tập 6: Tính Thời Gian Trung Bình Giữ Bóng

  Giả sử đội tuyển Việt Nam giữ bóng trong \(a\) phút ở hiệp 1 và \(b\) phút ở hiệp 2. Tính thời gian trung bình giữ bóng trong cả trận.

  Lời giải: Thời gian trung bình giữ bóng là \(\frac{a + b}{2}\) phút.

• Bài Tập 7: Tính Tỉ Lệ Thắng Trong Giải Đấu

  Đội tuyển Việt Nam tham gia \(c\) trận đấu và thắng \(d\) trận. Tính tỉ lệ thắng của đội tuyển Việt Nam trong giải đấu.

  Lời giải: Tỉ lệ thắng là \(\frac{d}{c}\).

• Bài Tập 8: Tính Tỉ Lệ Ghi Bàn Thành Công

  Đội tuyển Việt Nam sút \(e\) lần và ghi được \(f\) bàn. Tính tỉ lệ ghi bàn thành công của đội tuyển.

  Lời giải: Tỉ lệ ghi bàn thành công là \(\frac{f}{e}\).

• Bài Tập 9: Tính Xác Suất Ghi Bàn Trong Một Cú Sút

  Giả sử xác suất một cú sút ghi bàn là \(P(G)\). Nếu đội tuyển sút \(g\) lần, tính xác suất ít nhất 1 cú sút ghi bàn.

  Lời giải: Xác suất ít nhất 1 cú sút ghi bàn là \(1 - (1 - P(G))^g\).

• Bài Tập 10: Tính Xác Suất Thủ Môn Cản Phá Thành Công

  Giả sử xác suất thủ môn cản phá cú sút là \(P(S)\). Tính xác suất thủ môn cản phá thành công 3 cú sút liên tiếp.

  Lời giải: Xác suất cản phá thành công 3 cú sút liên tiếp là \(P(S)^3\).

Phương trình bậc hai có dạng tổng quát là:

Trong đó:

• \(a, b, c\) là các hằng số, \(a \neq 0\).
• \(x\) là ẩn số cần tìm.

Để giải phương trình bậc hai, ta tính biệt thức (Delta):

Với:

• Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt:
• \(x_1 = \frac{-b + \sqrt{\Delta}}{2a}\)
• \(x_2 = \frac{-b - \sqrt{\Delta}}{2a}\)
• Nếu \(\Delta = 0\), phương trình có một nghiệm kép:
• \(x = \frac{-b}{2a}\)
• Nếu \(\Delta < 0\), phương trình vô nghiệm (không có nghiệm thực).

Ví dụ:

Giải phương trình:

Lời giải:

• Tính biệt thức: \(\Delta = (-4)^2 - 4 \times 2 \times 2 = 16 - 16 = 0\)
• Vì \(\Delta = 0\), phương trình có nghiệm kép:
• \(x = \frac{-(-4)}{2 \times 2} = \frac{4}{4} = 1\)

Vậy nghiệm của phương trình là \(x = 1\).

Cho hàm số:

Nhiệm vụ của bạn là tính đạo hàm của hàm số này theo biến \(x\).

Các bước thực hiện:

1. Xác định từng thành phần của hàm số và áp dụng quy tắc đạo hàm cơ bản:
• \(\frac{d}{dx}(x^n) = nx^{n-1}\)
• \(\frac{d}{dx}(c) = 0\), với \(c\) là hằng số.
2. Tính đạo hàm của từng hạng tử:
• \(\frac{d}{dx}(3x^3) = 9x^2\)
• \(\frac{d}{dx}(-5x^2) = -10x\)
• \(\frac{d}{dx}(2x) = 2\)
• \(\frac{d}{dx}(-7) = 0\)
3. Cộng các kết quả lại để có đạo hàm của hàm số:
• \(f'(x) = 9x^2 - 10x + 2\)

Vậy đạo hàm của hàm số \(f(x) = 3x^3 - 5x^2 + 2x - 7\) là:

Bài tập này sẽ giúp bạn tính toán lực tác dụng lên một vật dựa trên các thông số đã cho.

Giả sử một vật có khối lượng \(m\) được đặt trên một mặt phẳng nghiêng với góc nghiêng \(\alpha\), không có ma sát. Lực tác dụng lên vật bởi trọng lực sẽ có thành phần dọc theo mặt phẳng nghiêng.

Để tính lực này, bạn cần sử dụng công thức sau:

Trong đó:

• \(F\) là lực tác dụng lên vật dọc theo mặt phẳng nghiêng (N).
• \(m\) là khối lượng của vật (kg).
• \(g\) là gia tốc trọng trường, thông thường \(g \approx 9.8 \, m/s^2\).
• \(\alpha\) là góc nghiêng của mặt phẳng (độ).

Các bước thực hiện:

1. Xác định khối lượng \(m\) của vật và góc nghiêng \(\alpha\) của mặt phẳng.
2. Thay giá trị \(m\), \(g\), và \(\alpha\) vào công thức:
• \(F = m \cdot g \cdot \sin(\alpha)\)
3. Tính toán kết quả để tìm lực \(F\).

Ví dụ:

Giả sử một vật có khối lượng \(m = 5 \, kg\) được đặt trên một mặt phẳng nghiêng với góc \(\alpha = 30^\circ\). Tính lực tác dụng lên vật dọc theo mặt phẳng nghiêng.

Lời giải:

• Khối lượng \(m = 5 \, kg\).
• Góc nghiêng \(\alpha = 30^\circ\).
• Gia tốc trọng trường \(g = 9.8 \, m/s^2\).
• Tính lực:
• \(F = 5 \cdot 9.8 \cdot \sin(30^\circ)\)
• \(F = 5 \cdot 9.8 \cdot 0.5 = 24.5 \, N\)

Vậy, lực tác dụng lên vật dọc theo mặt phẳng nghiêng là \(24.5 \, N\).

Bài tập này giúp bạn hiểu rõ hơn về cách tính toán điện trở trong các mạch điện, một phần kiến thức quan trọng trong vật lý. Chúng ta sẽ bắt đầu với các khái niệm cơ bản, sau đó áp dụng vào bài toán cụ thể.

4.1. Điện trở của các phần tử trong mạch

• Điện trở (R) của một phần tử trong mạch điện được xác định theo định luật Ohm, với công thức: \[ R = \frac{U}{I} \] trong đó \( U \) là điện áp (đơn vị Vôn), \( I \) là dòng điện (đơn vị Ampe).
• Các điện trở có thể được kết nối với nhau theo nhiều cách, trong đó phổ biến nhất là mắc nối tiếp và mắc song song.

4.2. Mắc điện trở nối tiếp

• Khi các điện trở được mắc nối tiếp, tổng điện trở của mạch là tổng các điện trở thành phần: \[ R_{\text{tổng}} = R_1 + R_2 + R_3 + \ldots \]
• Trong mạch nối tiếp, dòng điện chạy qua mỗi điện trở là như nhau, nhưng điện áp rơi trên mỗi điện trở có thể khác nhau.

4.3. Mắc điện trở song song

• Khi các điện trở được mắc song song, tổng điện trở của mạch được tính theo công thức: \[ \frac{1}{R_{\text{tổng}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots \]
• Trong mạch song song, điện áp trên mỗi điện trở là như nhau, nhưng dòng điện qua mỗi điện trở có thể khác nhau.

4.4. Bài tập ví dụ

1. Cho mạch điện gồm ba điện trở \( R_1 = 5 \, \Omega \), \( R_2 = 10 \, \Omega \), \( R_3 = 15 \, \Omega \) mắc nối tiếp. Tính điện trở tổng của mạch.

   Giải: \[ R_{\text{tổng}} = R_1 + R_2 + R_3 = 5 + 10 + 15 = 30 \, \Omega \]

2. Cho mạch điện gồm hai điện trở \( R_1 = 6 \, \Omega \), \( R_2 = 12 \, \Omega \) mắc song song. Tính điện trở tổng của mạch.

   Giải: \[ \frac{1}{R_{\text{tổng}}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{6} + \frac{1}{12} = \frac{2}{12} + \frac{1}{12} = \frac{3}{12} = \frac{1}{4} \]

   Do đó: \[ R_{\text{tổng}} = 4 \, \Omega \]

Bài tập này yêu cầu các em học sinh chia động từ trong ngoặc theo thì và ngữ cảnh phù hợp. Các câu sẽ có nội dung liên quan đến chủ đề bóng đá, giúp học sinh vừa học ngữ pháp tiếng Anh vừa có thể hiểu thêm về các thuật ngữ bóng đá.

Bài Tập 1

1. The match (start) __________ at 7 PM tonight. (Chia động từ trong ngoặc theo thì tương lai gần)
2. Vietnam (win) __________ the last AFF Cup final. (Chia động từ trong ngoặc theo thì quá khứ đơn)
3. The players (train) __________ hard all week. (Chia động từ trong ngoặc theo thì hiện tại hoàn thành)
4. If Vietnam (score) __________ one more goal, they will win the game. (Chia động từ trong ngoặc theo thì hiện tại đơn trong câu điều kiện loại 1)
5. By the time the final (end) __________, the fans will be celebrating. (Chia động từ trong ngoặc theo thì tương lai hoàn thành)

Bài Tập 2

1. He usually (watch) __________ every match that Vietnam plays. (Chia động từ trong ngoặc theo thì hiện tại đơn)
2. They (support) __________ the national team for many years. (Chia động từ trong ngoặc theo thì hiện tại hoàn thành)
3. After the game (finish) __________, we went to celebrate. (Chia động từ trong ngoặc theo thì quá khứ đơn)
4. The coach (plan) __________ the strategy for the next match right now. (Chia động từ trong ngoặc theo thì hiện tại tiếp diễn)
5. Vietnam (face) __________ their biggest rival in the final. (Chia động từ trong ngoặc theo thì tương lai đơn)

Bài Tập 3

Hoàn thành đoạn văn dưới đây bằng cách chia đúng dạng của động từ trong ngoặc:

“Vietnam __________ (compete) in the final match of the AFF Cup. The team __________ (prepare) thoroughly for this moment. If they __________ (win) the game, it __________ (be) a historic victory. All the fans __________ (watch) the match eagerly, hoping that Vietnam __________ (lift) the trophy once again.”

Bài tập sau đây yêu cầu các bạn điền giới từ phù hợp vào chỗ trống trong các câu tiếng Anh dưới đây. Mỗi câu đều được thiết kế để giúp bạn ôn tập và củng cố kiến thức về cách sử dụng giới từ trong tiếng Anh. Hãy đọc kỹ từng câu và suy nghĩ về giới từ nào sẽ phù hợp nhất.

1. The match between Vietnam and Thailand will take place ___ the National Stadium.
2. Fans are looking forward ___ the upcoming final.
3. The team arrived ___ the stadium two hours before the match.
4. Vietnam is competing ___ the championship title.
5. Tickets for the match sold out ___ a few hours.
6. The players are confident ___ their ability to win the final.
7. The coach emphasized the importance ___ teamwork in the upcoming match.
8. Many supporters traveled ___ Vietnam to cheer for their team.
9. Everyone is excited ___ the big match tomorrow night.
10. The victory ___ the final would be a great achievement for Vietnam.

Hãy viết câu trả lời của bạn ra giấy hoặc gõ vào file văn bản để kiểm tra với đáp án chuẩn. Sau khi hoàn thành, bạn có thể tham khảo lời giải chi tiết và lý do sử dụng từng giới từ.

Dưới đây là các bài tập tính tích phân của các hàm số thường gặp, giúp bạn luyện tập và củng cố kiến thức về tích phân trong toán học.

1. Tính tích phân xác định của hàm số:
   \[ \int_{0}^{1} (3x^2 + 2x + 1) \, dx \]
2. Tính tích phân không xác định của hàm số:
   \[ \int (e^{2x} \cdot \sin(x)) \, dx \]
3. Tính tích phân của hàm số trên đoạn \([1, 3]\):
   \[ \int_{1}^{3} \frac{1}{x^2 + 4} \, dx \]
4. Tính tích phân của hàm số bậc ba trên khoảng \([-2, 2]\):
   \[ \int_{-2}^{2} (x^3 - 3x^2 + 2x) \, dx \]
5. Tìm tích phân không xác định của hàm số:
   \[ \int \frac{1}{\sqrt{x^2 - 1}} \, dx \]
6. Tính diện tích hình phẳng giới hạn bởi đường cong và trục hoành:
   \[ \text{Diện tích} = \int_{0}^{2} \left| x^2 - 4x + 3 \right| \, dx \]

Hãy giải quyết từng bài tập một cách cẩn thận và đối chiếu kết quả để đảm bảo sự chính xác. Những bài tập này sẽ giúp bạn hiểu rõ hơn về cách tính tích phân cũng như ứng dụng của tích phân trong thực tế.

Trong bài tập này, chúng ta sẽ tìm hiểu cách giải hệ phương trình tuyến tính bằng phương pháp thế và phương pháp cộng đại số. Hệ phương trình tuyến tính thường gặp trong nhiều bài toán thực tế, chẳng hạn như trong phân tích kết quả các trận đấu bóng đá hoặc trong các mô hình kinh tế.

Bước 1: Xác định hệ phương trình

Giả sử chúng ta có hệ phương trình tuyến tính sau:

Bước 2: Giải hệ phương trình bằng phương pháp thế

1. Giải phương trình thứ hai để tìm x theo y:

\[ x = 4y - 2 \]

2. Thế giá trị của x vào phương trình thứ nhất:

\[ 2(4y - 2) + 3y = 7 \]

3. Giải phương trình này để tìm y:

\[ 8y - 4 + 3y = 7 \\ 11y = 11 \\ y = 1 \]

4. Thế giá trị của y vào phương trình tìm được ở bước 1:

\[ x = 4(1) - 2 = 2 \]

Bước 3: Kiểm tra kết quả

Thay các giá trị x = 2 và y = 1 vào cả hai phương trình ban đầu để kiểm tra:

• \(2(2) + 3(1) = 4 + 3 = 7\)
• \(2 - 4(1) = 2 - 4 = -2\)

Vậy hệ phương trình đã giải đúng, nghiệm của hệ là \(x = 2\), \(y = 1\).

Chúc các bạn làm bài tập thành công!

Trong bài tập này, chúng ta sẽ phân tích chuyển động của một vật dưới tác động của các lực khác nhau. Đây là bài tập quan trọng giúp bạn nắm vững kiến thức về cơ học và áp dụng chúng vào các tình huống thực tế.

Đề bài:

Cho một vật có khối lượng \( m \) kg, chuyển động trên mặt phẳng ngang không ma sát dưới tác động của lực \( F \) N. Vật bắt đầu chuyển động từ trạng thái nghỉ tại vị trí \( x_0 \) với vận tốc ban đầu \( v_0 = 0 \).

• Câu 1: Xác định phương trình chuyển động của vật theo thời gian \( t \).
• Câu 2: Tính vận tốc của vật tại thời điểm \( t = 5 \) giây.
• Câu 3: Xác định quãng đường vật đi được sau 10 giây.

Hướng dẫn giải:

1. Trước hết, áp dụng định luật II Newton để thiết lập phương trình chuyển động:

\[
F = m \cdot a \quad \Rightarrow \quad a = \frac{F}{m}
\]

2. Phương trình vận tốc theo thời gian được xác định bởi:

\[
v(t) = v_0 + a \cdot t = 0 + \frac{F}{m} \cdot t
\]

3. Phương trình vị trí của vật theo thời gian là:

\[
x(t) = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 = x_0 + \frac{1}{2} \cdot \frac{F}{m} \cdot t^2
\]

4. Thay số và tính toán:
• Vận tốc tại thời điểm \( t = 5 \) giây:

\[
v(5) = \frac{F}{m} \cdot 5 \, \text{(m/s)}
\]

• Quãng đường sau 10 giây:

\[
x(10) = x_0 + \frac{1}{2} \cdot \frac{F}{m} \cdot 10^2 \, \text{(m)}
\]

Chú ý rằng, các kết quả cụ thể phụ thuộc vào giá trị cụ thể của \( F \) và \( m \) trong đề bài. Để hiểu rõ hơn về các bài tập tương tự, các em có thể tham khảo các trận đấu chung kết sắp tới, nơi những phân tích chuyển động của cầu thủ cũng có thể được áp dụng trong các bài toán thực tế.

Trong bài tập này, bạn sẽ rèn luyện kỹ năng viết lại câu sao cho nghĩa của câu không thay đổi. Đây là một phần quan trọng trong việc nâng cao khả năng ngữ pháp và từ vựng tiếng Anh.

Hướng dẫn:

1. Đọc kỹ câu gốc và xác định cấu trúc ngữ pháp được sử dụng.
2. Xem xét các từ đồng nghĩa, các cấu trúc ngữ pháp khác có thể thay thế mà vẫn giữ nguyên ý nghĩa của câu.
3. Viết lại câu bằng cách sử dụng các cấu trúc ngữ pháp khác nhau, có thể bao gồm:
   • Câu bị động và chủ động.
   • Sử dụng các từ nối như "although", "despite", "however", v.v.
   • Chuyển từ danh từ sang động từ hoặc ngược lại.
   • Dùng cấu trúc đảo ngữ để nhấn mạnh ý.
4. So sánh câu viết lại với câu gốc để đảm bảo rằng ý nghĩa vẫn được giữ nguyên.

Ví dụ bài tập:

• Câu gốc: "She cannot attend the meeting because she is sick."
• Viết lại: "Because of her sickness, she cannot attend the meeting."

Bài tập thực hành:

• (1) "He didn’t know how to solve the problem, so he asked his teacher."
• (2) "I will finish the project by tomorrow if I start working now."
• (3) "Despite the heavy rain, they went on a picnic."

Hãy thử viết lại các câu trên sao cho nghĩa không đổi và đảm bảo rằng cấu trúc câu vẫn hợp lý. Chúc bạn luyện tập tốt!