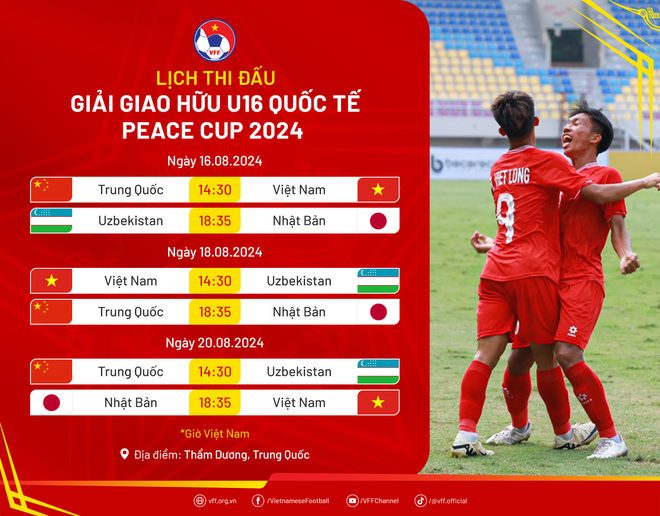
Chủ đề lịch thi đấu bóng đá việt nam và trung quốc: Lịch thi đấu bóng đá giữa Việt Nam và Trung Quốc luôn là chủ đề nóng hổi, thu hút sự chú ý lớn từ người hâm mộ. Bài viết này cung cấp thông tin chi tiết và đầy đủ về các trận đấu sắp diễn ra giữa hai đội tuyển, bao gồm thời gian, địa điểm và những phân tích chuyên sâu về lực lượng và chiến thuật.
Mục lục
- Lịch thi đấu bóng đá Việt Nam và Trung Quốc
- Mục lục tổng hợp các thông tin về lịch thi đấu
- Dạng bài tập có lời giải hoàn chỉnh (Môn Toán)
- Dạng bài 1: Giải phương trình bậc 2
- Dạng bài 2: Hệ phương trình tuyến tính
- Dạng bài 3: Tính đạo hàm và ứng dụng
- Dạng bài 4: Tích phân hàm số
- Dạng bài 5: Xác suất trong các bài toán thực tế
- Dạng bài 6: Giải bất đẳng thức
- Dạng bài 7: Hàm số và tính chất
- Dạng bài 8: Tính diện tích hình phẳng
- Dạng bài 9: Dãy số và giới hạn
- Dạng bài 10: Tìm giá trị lớn nhất, nhỏ nhất của hàm số
Lịch thi đấu bóng đá Việt Nam và Trung Quốc
Lịch thi đấu giữa đội tuyển Việt Nam và Trung Quốc luôn nhận được sự quan tâm lớn từ người hâm mộ bóng đá. Các trận đấu giữa hai đội thường nằm trong các giải đấu quan trọng như Vòng loại World Cup, các trận giao hữu quốc tế hoặc các giải đấu khu vực.
Thông tin chung
Đội tuyển Việt Nam và Trung Quốc đã nhiều lần đối đầu trong quá khứ. Mặc dù Trung Quốc thường chiếm ưu thế, nhưng trong các năm gần đây, đội tuyển Việt Nam đã có những thành tích đáng chú ý. Dưới đây là một số thông tin chi tiết về lịch thi đấu giữa hai đội trong các sự kiện lớn.
Lịch thi đấu giao hữu tháng 10/2023
- Ngày thi đấu: 10/10/2023
- Địa điểm: Sân vận động tại Trung Quốc
- Giải đấu: Giao hữu quốc tế trong khuôn khổ FIFA Days
- Đối thủ: Đội tuyển quốc gia Trung Quốc
- Trực tiếp: FPT Play, VTV5, VTV6
Đây là trận đấu giao hữu, là cơ hội tốt để đội tuyển Việt Nam chuẩn bị cho các trận đấu trong khuôn khổ vòng loại World Cup 2026 sắp tới.
Lịch thi đấu tại vòng loại World Cup 2026
Đội tuyển Việt Nam sẽ tiếp tục thi đấu vòng loại thứ 2 World Cup 2026, khu vực châu Á. Đây là cơ hội lớn để đội nhà giành tấm vé vào vòng chung kết.
- Đối thủ: Trung Quốc
- Thời gian: Tháng 11/2023 (dự kiến)
- Địa điểm: Việt Nam và Trung Quốc (thi đấu lượt đi và về)
Thành tích đối đầu giữa Việt Nam và Trung Quốc
| Năm | Giải đấu | Kết quả |
|---|---|---|
| 2022 | Vòng loại World Cup 2022 | Việt Nam 3 - 1 Trung Quốc |
| 2021 | Vòng loại World Cup 2022 | Trung Quốc 3 - 2 Việt Nam |
| 2012 | Giao hữu | Trung Quốc 6 - 1 Việt Nam |
Những điểm đáng chú ý
- Trận thắng của đội tuyển Việt Nam trước Trung Quốc vào ngày 01/02/2022 tại SVĐ Mỹ Đình trong khuôn khổ vòng loại World Cup 2022 là một trong những chiến thắng lịch sử.
- Thời gian sắp tới, hai đội sẽ có cơ hội gặp lại nhau trong các trận giao hữu và vòng loại World Cup 2026.
- Người hâm mộ có thể theo dõi các trận đấu thông qua các kênh truyền hình phổ biến tại Việt Nam như VTV và FPT Play.
Kết luận
Trận đấu giữa Việt Nam và Trung Quốc luôn mang đến sự hấp dẫn và căng thẳng. Với sự phát triển vượt bậc của bóng đá Việt Nam trong những năm gần đây, người hâm mộ có quyền hy vọng vào những kết quả tích cực trong các trận đối đầu sắp tới.

.png)
Mục lục tổng hợp các thông tin về lịch thi đấu
Dưới đây là danh sách tổng hợp các nội dung quan trọng liên quan đến lịch thi đấu bóng đá giữa đội tuyển Việt Nam và Trung Quốc, bao gồm thời gian, địa điểm và các yếu tố liên quan khác mà người hâm mộ không thể bỏ qua.
- Lịch thi đấu chính thức
Lịch thi đấu giao hữu và vòng loại giữa Việt Nam và Trung Quốc trong năm 2023 và các năm gần đây, bao gồm ngày, giờ và sân đấu.
- Kết quả đối đầu lịch sử
Thống kê các kết quả đối đầu giữa hai đội trong các kỳ World Cup, vòng loại khu vực và các giải đấu khác.
- Phân tích phong độ hai đội
Cập nhật phong độ hiện tại của đội tuyển Việt Nam và Trung Quốc trước mỗi trận đấu, dựa trên kết quả thi đấu gần nhất.
- Danh sách cầu thủ và chiến thuật
Thông tin chi tiết về đội hình, danh sách cầu thủ ra sân và chiến thuật của cả hai đội trong các trận đấu sắp tới.
- Thông tin phát sóng trực tiếp
Các kênh truyền hình và nền tảng phát sóng trực tiếp các trận đấu giữa Việt Nam và Trung Quốc.
- Ý kiến chuyên gia
Nhận định từ các chuyên gia bóng đá về diễn biến và kết quả các trận đấu giữa hai đội.
- Những khoảnh khắc đáng nhớ
Những khoảnh khắc nổi bật, bàn thắng đẹp mắt và các sự kiện đáng nhớ trong lịch sử đối đầu giữa Việt Nam và Trung Quốc.
- Cơ hội tiến sâu tại các giải đấu
Phân tích cơ hội của đội tuyển Việt Nam và Trung Quốc trong các giải đấu lớn như vòng loại World Cup và Asian Cup.
- Nhận định và dự đoán
Dự đoán kết quả trận đấu sắp tới giữa Việt Nam và Trung Quốc từ các chuyên gia và người hâm mộ.
Với sự chuẩn bị kỹ lưỡng từ cả hai đội, các trận đấu giữa Việt Nam và Trung Quốc hứa hẹn sẽ mang lại nhiều cảm xúc và bất ngờ cho người hâm mộ.
Dạng bài tập có lời giải hoàn chỉnh (Môn Toán)
Dưới đây là các dạng bài tập môn Toán có lời giải hoàn chỉnh, chủ yếu xoay quanh các khái niệm về hoán vị, chỉnh hợp, tổ hợp. Các bài tập này giúp củng cố kiến thức lý thuyết và rèn luyện kỹ năng giải bài toán tổ hợp một cách hệ thống.
Bài tập 1: Sắp xếp các bạn vào ghế
Sắp xếp năm bạn học sinh vào một ghế dài 5 chỗ. Trong đó, một bạn phải ngồi ở vị trí chính giữa.
- Tính số cách sắp xếp các bạn học sinh.
- Giải thích chi tiết cách tính.
Bài tập 2: Tính chỉnh hợp
Cho 3 viên bi đen và 4 viên bi đỏ. Hãy tính số cách chọn 3 viên bi để sắp xếp theo thứ tự.
Bài tập 3: Hoán vị các ký tự
Tính số hoán vị của từ "COMPUTER".
Bài tập 4: Chọn đội bóng đá
Có 20 cầu thủ, cần chọn ra 11 cầu thủ để thi đấu chính thức. Hãy tính số cách chọn.
Bài tập 5: Tổ hợp với điều kiện
Cho một tập hợp có 8 phần tử. Hãy tính số tổ hợp chập 3 từ tập hợp đó.
Bài tập 6: Giải hệ thức truy hồi
Cho hệ thức truy hồi sau, hãy giải và tìm giá trị n-th:
f(n) = f(n-1) + 2f(n-2)
Bài tập 7: Chọn sinh viên
Chọn 3 sinh viên từ nhóm 5 sinh viên để sắp xếp đứng thành hàng. Tính số cách chọn.
Bài tập 8: Phân chia giải thưởng
Có 100 người tham gia một cuộc thi. Tính số cách chọn người nhận giải nhất, nhì và ba.
Bài tập 9: Phân tích chữ số
Số cách khác nhau để sắp xếp các ký tự trong từ "MISSISSIPI".
Bài tập 10: Tổ hợp chập k của n
Tính tổ hợp chập 4 của 10 phần tử.

Dạng bài 1: Giải phương trình bậc 2
Phương trình bậc 2 là dạng phương trình có dạng tổng quát như sau:
Trong đó:
- \(a\), \(b\), \(c\) là các hằng số đã cho, với \(a \neq 0\)
- \(x\) là ẩn số cần tìm
Để giải phương trình bậc 2, ta sử dụng công thức nghiệm:
Quy trình giải phương trình bậc 2:
- Xác định các hệ số \(a\), \(b\), \(c\) từ phương trình.
- Tính biệt thức \(\Delta = b^2 - 4ac\).
- Xét dấu của \(\Delta\):
- Nếu \(\Delta > 0\), phương trình có 2 nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có nghiệm kép \(x = \frac{-b}{2a}\).
- Nếu \(\Delta < 0\), phương trình vô nghiệm.
- Áp dụng công thức nghiệm để tìm \(x\).
Ví dụ: Giải phương trình sau:
Lời giải:
- Hệ số \(a = 2\), \(b = -4\), \(c = 2\).
- Tính biệt thức \(\Delta = (-4)^2 - 4(2)(2) = 16 - 16 = 0\).
- Vì \(\Delta = 0\), phương trình có nghiệm kép: \[ x = \frac{-(-4)}{2(2)} = \frac{4}{4} = 1 \]
- Kết luận: Phương trình có nghiệm kép \(x = 1\).

Dạng bài 2: Hệ phương trình tuyến tính
Hệ phương trình tuyến tính là một tập hợp các phương trình dạng tuyến tính, trong đó các biến xuất hiện ở bậc nhất. Hệ phương trình có dạng tổng quát như sau:
Trong đó:
- \(a_1, b_1, c_1\) và \(a_2, b_2, c_2\) là các hệ số đã cho.
- \(x\) và \(y\) là các ẩn số cần tìm.
Các bước giải hệ phương trình tuyến tính 2 ẩn:
- Chọn một trong hai phương trình, biến đổi để biểu diễn một ẩn theo ẩn còn lại.
- Thay biểu thức của ẩn vừa tìm được vào phương trình còn lại để tìm ra giá trị của một ẩn.
- Sau khi tìm được giá trị của một ẩn, thay vào phương trình vừa biến đổi để tìm giá trị của ẩn còn lại.
- Kết luận nghiệm của hệ phương trình.
Ví dụ: Giải hệ phương trình sau:
Lời giải:
- Từ phương trình thứ hai: \(4x - y = 1 \Rightarrow y = 4x - 1\).
- Thay \(y = 4x - 1\) vào phương trình thứ nhất: \[ 2x + 3(4x - 1) = 5 \] \[ 2x + 12x - 3 = 5 \Rightarrow 14x = 8 \Rightarrow x = \frac{8}{14} = \frac{4}{7} \]
- Thay \(x = \frac{4}{7}\) vào biểu thức \(y = 4x - 1\): \[ y = 4\left(\frac{4}{7}\right) - 1 = \frac{16}{7} - 1 = \frac{16}{7} - \frac{7}{7} = \frac{9}{7} \]
- Kết luận: Hệ phương trình có nghiệm \(x = \frac{4}{7}, y = \frac{9}{7}\).

Dạng bài 3: Tính đạo hàm và ứng dụng
Đạo hàm là một khái niệm cơ bản trong giải tích, biểu thị sự thay đổi của một hàm số khi biến số thay đổi. Dạng bài tính đạo hàm không chỉ yêu cầu học sinh tính toán mà còn cần biết cách áp dụng kết quả vào các bài toán thực tế.
1. Công thức cơ bản
- Đạo hàm của hàm số \(f(x)\) tại điểm \(x = a\) được định nghĩa là:
\[
f'(a) = \lim_{{h \to 0}} \frac{f(a+h) - f(a)}{h}
\]
- Đạo hàm của một số hàm số cơ bản:
- \(\frac{d}{dx} [c] = 0\) (với \(c\) là hằng số)
- \(\frac{d}{dx} [x^n] = n \cdot x^{n-1}\)
- \(\frac{d}{dx} [\sin(x)] = \cos(x)\)
- \(\frac{d}{dx} [\cos(x)] = -\sin(x)\)
- \(\frac{d}{dx} [e^x] = e^x\)
- \(\frac{d}{dx} [\ln(x)] = \frac{1}{x}\) (với \(x > 0\))
2. Quy tắc tính đạo hàm
- Quy tắc tổng: \(\frac{d}{dx} [f(x) + g(x)] = f'(x) + g'(x)\)
- Quy tắc tích: \(\frac{d}{dx} [f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x) \cdot g'(x)\)
- Quy tắc thương: \(\frac{d}{dx} \left[\frac{f(x)}{g(x)}\right] = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{[g(x)]^2}\) (với \(g(x) \neq 0\))
- Quy tắc chuỗi: \(\frac{d}{dx} [f(g(x))] = f'(g(x)) \cdot g'(x)\)
3. Ứng dụng của đạo hàm
3.1. Tìm tiếp tuyến của đồ thị hàm số
Tiếp tuyến của đồ thị hàm số \(y = f(x)\) tại điểm \(x = a\) có phương trình:
\[
y = f'(a) \cdot (x - a) + f(a)
\]
3.2. Tìm cực trị của hàm số
Cực trị của hàm số là điểm tại đó đạo hàm bằng 0:
\[
f'(x) = 0
\]
Để xác định đó là cực đại hay cực tiểu, ta xét đạo hàm cấp hai:
\[
f''(x) > 0 \Rightarrow \text{Cực tiểu}, \quad f''(x) < 0 \Rightarrow \text{Cực đại}
\]
3.3. Ứng dụng trong vật lý
Trong vật lý, đạo hàm được dùng để biểu diễn tốc độ thay đổi, chẳng hạn như:
- Vận tốc là đạo hàm của quãng đường theo thời gian: \(v(t) = s'(t)\).
- Gia tốc là đạo hàm của vận tốc theo thời gian: \(a(t) = v'(t)\).
4. Bài tập ví dụ
Ví dụ: Tính đạo hàm của hàm số \(f(x) = 3x^2 - 5x + 4\).
Lời giải:
\[
f'(x) = \frac{d}{dx} [3x^2 - 5x + 4] = 6x - 5
\]
Vậy đạo hàm của hàm số \(f(x)\) là \(f'(x) = 6x - 5\).
XEM THÊM:
Dạng bài 4: Tích phân hàm số
Tích phân hàm số là một khái niệm cơ bản và quan trọng trong giải tích. Dưới đây là các bước để giải một bài toán tích phân hàm số cùng một số ví dụ minh họa.
Bước 1: Xác định hàm số cần tính tích phân
Hàm số cần tính tích phân có thể được cho dưới dạng hàm số đơn giản hoặc phức tạp, ví dụ:
- \(f(x) = x^2\)
- \(f(x) = \sin(x)\)
- \(f(x) = e^x\)
Bước 2: Xác định cận của tích phân
Các cận của tích phân thường được xác định dựa trên khoảng cách mà bạn cần tính diện tích dưới đường cong. Ví dụ, nếu bạn cần tính diện tích dưới đường cong từ \(x = 0\) đến \(x = 2\), thì tích phân sẽ có dạng:
Bước 3: Áp dụng công thức tích phân
Tuỳ thuộc vào dạng của hàm số \(f(x)\), bạn có thể áp dụng các công thức tích phân cơ bản để tìm ra giá trị của tích phân. Dưới đây là một số công thức tích phân cơ bản:
- \(\int x^n dx = \frac{x^{n+1}}{n+1} + C\), với \(n \neq -1\)
- \(\int e^x dx = e^x + C\)
- \(\int \sin(x) dx = -\cos(x) + C\)
- \(\int \cos(x) dx = \sin(x) + C\)
Với \(C\) là hằng số tích phân.
Bước 4: Tính giá trị của tích phân
Sau khi áp dụng công thức tích phân, ta sẽ thực hiện việc tính toán giá trị cụ thể. Ví dụ, với tích phân:
Ta có thể tính như sau:
- Bước 1: Tính nguyên hàm của \(x^2\): \(\frac{x^3}{3}\)
- Bước 2: Thay cận vào nguyên hàm và tính toán:
Ví dụ minh họa khác
Giả sử bạn cần tính tích phân sau:
Thực hiện các bước như trên, ta có:
- Nguyên hàm của \(\sin(x)\) là \(-\cos(x)\)
- Thay cận vào nguyên hàm:
Kết luận
Tích phân hàm số giúp chúng ta tính toán diện tích dưới đường cong hoặc tổng hợp các lượng nhỏ lại thành một lượng tổng quát. Việc nắm vững các bước giải tích phân là vô cùng cần thiết để hiểu sâu hơn về giải tích và áp dụng vào các bài toán thực tế.

Dạng bài 5: Xác suất trong các bài toán thực tế
Xác suất là một lĩnh vực quan trọng trong toán học, được ứng dụng rộng rãi trong nhiều khía cạnh của cuộc sống, từ dự đoán thời tiết, phân tích rủi ro tài chính đến các quyết định chiến lược trong thể thao. Trong bài toán thực tế, việc tính toán xác suất giúp chúng ta đưa ra những quyết định thông minh và có cơ sở.
Ví dụ 1: Xác suất đội tuyển Việt Nam thắng trong một trận đấu
Giả sử trong một trận đấu giữa đội tuyển Việt Nam và Trung Quốc, chúng ta biết rằng:
- Xác suất đội tuyển Việt Nam thắng là \( P(V) = 0,3 \).
- Xác suất đội tuyển Trung Quốc thắng là \( P(T) = 0,5 \).
- Xác suất hai đội hòa nhau là \( P(H) = 0,2 \).
Để kiểm tra tính hợp lý của các xác suất này, chúng ta cần đảm bảo rằng tổng xác suất của các kết quả phải bằng 1:
\[
P(V) + P(T) + P(H) = 0,3 + 0,5 + 0,2 = 1,0
\]
Vì tổng các xác suất bằng 1, các xác suất này là hợp lý. Nếu muốn dự đoán khả năng đội tuyển Việt Nam không thua (tức là hoặc thắng hoặc hòa), ta có:
\[
P(\text{Không thua}) = P(V) + P(H) = 0,3 + 0,2 = 0,5
\]
Như vậy, xác suất đội tuyển Việt Nam không thua trong trận đấu này là 0,5, tức 50%.
Ví dụ 2: Xác suất xảy ra các sự kiện độc lập
Xét một trường hợp khác, nếu đội tuyển Việt Nam thi đấu hai trận liên tiếp, và xác suất thắng mỗi trận là \( P(V) = 0,3 \), các trận đấu này là độc lập với nhau. Xác suất đội tuyển Việt Nam thắng cả hai trận được tính như sau:
\[
P(V \text{ cả hai trận}) = P(V) \times P(V) = 0,3 \times 0,3 = 0,09
\]
Như vậy, xác suất đội tuyển Việt Nam thắng cả hai trận liên tiếp là 0,09, tức 9%.
Ví dụ 3: Xác suất có điều kiện
Trong một giải đấu, nếu chúng ta biết rằng đội tuyển Việt Nam đã thắng trận đầu tiên, thì xác suất họ thắng trận thứ hai có thể thay đổi dựa trên thông tin mới này. Giả sử xác suất thắng trận thứ hai nếu đã thắng trận đầu là \( P(V_2|V_1) = 0,6 \). Xác suất đội tuyển Việt Nam thắng cả hai trận sẽ là:
\[
P(V_1 \cap V_2) = P(V_1) \times P(V_2|V_1) = 0,3 \times 0,6 = 0,18
\]
Vì vậy, xác suất đội tuyển Việt Nam thắng cả hai trận khi biết rằng họ đã thắng trận đầu là 0,18, tức 18%.
Các ví dụ trên minh họa cách tính toán xác suất trong các tình huống thực tế, giúp chúng ta có cái nhìn rõ ràng hơn về khả năng xảy ra của các sự kiện và hỗ trợ trong việc ra quyết định chính xác.

Dạng bài 6: Giải bất đẳng thức
Trong toán học, bất đẳng thức là một mệnh đề so sánh giữa hai biểu thức mà trong đó có thể xác định được mối quan hệ lớn hơn, nhỏ hơn hoặc bằng nhau. Dưới đây là hướng dẫn chi tiết cách giải các bài toán về bất đẳng thức.
Bước 1: Xác định dạng bất đẳng thức
Trước tiên, ta cần xác định dạng của bất đẳng thức. Các dạng phổ biến bao gồm:
- Bất đẳng thức tuyến tính: có dạng \(ax + b > 0\) hoặc \(ax + b < 0\).
- Bất đẳng thức bậc hai: có dạng \(ax^2 + bx + c > 0\) hoặc \(ax^2 + bx + c < 0\).
- Bất đẳng thức chứa căn: bao gồm các bất đẳng thức dạng \(\sqrt{f(x)} > g(x)\) hoặc \(\sqrt{f(x)} < g(x)\).
Bước 2: Tìm điều kiện của biến số
Trong các bài toán bất đẳng thức, cần xác định điều kiện của biến số để đảm bảo các biểu thức có nghĩa. Ví dụ, nếu bất đẳng thức chứa căn bậc hai, ta cần đảm bảo rằng biểu thức trong căn phải không âm:
\[
f(x) \geq 0
\]
Bước 3: Giải bất đẳng thức
Sau khi xác định được điều kiện của biến số, ta tiến hành giải bất đẳng thức. Ví dụ, đối với bất đẳng thức bậc hai, ta có thể sử dụng phương pháp xét dấu hoặc công thức nghiệm của phương trình bậc hai để tìm các khoảng nghiệm:
\[
ax^2 + bx + c > 0
\]
Ta sẽ tính biệt thức \(\Delta = b^2 - 4ac\) để xác định số nghiệm và sau đó xét dấu biểu thức.
Bước 4: Lập bảng xét dấu
Sau khi tìm được các nghiệm, ta lập bảng xét dấu để xác định khoảng nào của biến thỏa mãn bất đẳng thức đã cho. Điều này đặc biệt hữu ích trong việc xử lý các bất đẳng thức phức tạp hơn, chẳng hạn như bất đẳng thức chứa nhiều ẩn số hoặc bất đẳng thức phi tuyến tính.
Bước 5: Kết luận
Từ bảng xét dấu, ta rút ra các khoảng giá trị của biến thỏa mãn bất đẳng thức ban đầu. Đừng quên kiểm tra lại điều kiện ban đầu của biến để đảm bảo rằng các nghiệm nằm trong khoảng đã xét là hợp lý.
Dưới đây là một ví dụ minh họa cụ thể:
Giải bất đẳng thức:
\[
x^2 - 5x + 6 > 0
\]
Giải:
- Tính biệt thức: \(\Delta = (-5)^2 - 4 \times 1 \times 6 = 1\)
- Tìm nghiệm của phương trình: \(x_1 = 2\), \(x_2 = 3\)
- Lập bảng xét dấu và tìm khoảng nghiệm: \(x < 2\) hoặc \(x > 3\)
Kết luận: Bất đẳng thức có nghiệm khi \(x < 2\) hoặc \(x > 3\).
Dạng bài 7: Hàm số và tính chất
Hàm số là một khái niệm cơ bản trong Toán học, biểu diễn mối quan hệ giữa các đại lượng. Một hàm số có thể được xác định bởi một công thức hoặc một biểu đồ, và nó giúp chúng ta hiểu rõ hơn về cách các giá trị thay đổi tương ứng với nhau.
Bước 1: Xác định miền xác định của hàm số
Miền xác định của một hàm số là tập hợp tất cả các giá trị của biến số mà hàm số đó được xác định. Chẳng hạn, đối với hàm số \( f(x) = \frac{1}{x-2} \), miền xác định là \( \mathbb{R} \setminus \{2\} \) (tập hợp tất cả các số thực trừ 2).
Bước 2: Xét tính chất chẵn lẻ của hàm số
Hàm số \( f(x) \) được gọi là hàm chẵn nếu \( f(-x) = f(x) \) với mọi \( x \) trong miền xác định. Ngược lại, hàm số được gọi là hàm lẻ nếu \( f(-x) = -f(x) \).
- Ví dụ: Hàm số \( f(x) = x^2 \) là hàm chẵn vì \( f(-x) = (-x)^2 = x^2 = f(x) \).
- Hàm số \( f(x) = x^3 \) là hàm lẻ vì \( f(-x) = (-x)^3 = -x^3 = -f(x) \).
Bước 3: Xét sự biến thiên của hàm số
Sự biến thiên của hàm số thể hiện qua đạo hàm của hàm số đó. Xét hàm số \( f(x) \), ta tính đạo hàm \( f'(x) \) để xác định khoảng đồng biến (hàm số tăng) hoặc nghịch biến (hàm số giảm).
Ví dụ, với hàm số \( f(x) = x^3 - 3x + 2 \), ta có:
\[
f'(x) = 3x^2 - 3
\]
Ta giải bất phương trình \( f'(x) > 0 \) để tìm khoảng đồng biến và \( f'(x) < 0 \) để tìm khoảng nghịch biến.
Bước 4: Tìm cực trị của hàm số
Cực trị của hàm số là giá trị lớn nhất hoặc nhỏ nhất mà hàm số đạt được trên một khoảng nào đó. Để tìm cực trị, ta giải phương trình \( f'(x) = 0 \) và xác định dấu của đạo hàm \( f'(x) \) ở hai bên của nghiệm đó.
Ví dụ, nếu hàm số \( f(x) = x^3 - 3x + 2 \) có đạo hàm \( f'(x) = 3x^2 - 3 \), ta giải phương trình:
\[
f'(x) = 3x^2 - 3 = 0 \Rightarrow x = \pm 1
\]
Từ đó, ta xét dấu của \( f'(x) \) trên các khoảng \( (-\infty, -1) \), \( (-1, 1) \), và \( (1, \infty) \) để xác định cực trị.
Bước 5: Vẽ đồ thị hàm số
Sau khi đã xác định đầy đủ các tính chất của hàm số, ta có thể vẽ đồ thị của nó. Đồ thị giúp minh họa trực quan sự biến thiên của hàm số và các điểm đặc biệt như cực trị, điểm uốn.
Đối với hàm số \( f(x) = x^3 - 3x + 2 \), đồ thị sẽ có hình dạng như sau:
Hàm số có cực trị tại các điểm \( x = -1 \) và \( x = 1 \), đồ thị cắt trục tung tại điểm \( (0, 2) \).

Dạng bài 8: Tính diện tích hình phẳng
Trong toán học, diện tích hình phẳng giữa hai đồ thị của hai hàm số là phần diện tích nằm giữa hai đường cong được xác định bởi các hàm số đó trong một khoảng nhất định. Để tính diện tích này, ta sử dụng công cụ tích phân.
Giả sử cần tính diện tích hình phẳng giới hạn bởi các đồ thị của hai hàm số \( f(x) \) và \( g(x) \) trên đoạn \( [a, b] \), ta sẽ tính diện tích theo công thức sau:
\[
S = \int_{a}^{b} |f(x) - g(x)| \, dx
\]
Trong đó:
- \( S \): Diện tích hình phẳng cần tính.
- \( f(x) \) và \( g(x) \): Hai hàm số xác định các đường cong.
- \( a \) và \( b \): Các giới hạn của khoảng cần tính diện tích.
- \( |f(x) - g(x)| \): Độ dài của đoạn thẳng thẳng đứng giữa hai đồ thị tại điểm \( x \).
Ví dụ: Tính diện tích hình phẳng giới hạn bởi hai đồ thị của các hàm số \( f(x) = x^2 \) và \( g(x) = x + 2 \) trên đoạn \( [0, 2] \).
Ta có:
\[
S = \int_{0}^{2} |x^2 - (x + 2)| \, dx
\]
Bước 1: Tìm điểm giao nhau của hai đồ thị bằng cách giải phương trình \( x^2 = x + 2 \).
Giải phương trình:
\[
x^2 - x - 2 = 0
\]
Phương trình có nghiệm \( x = -1 \) và \( x = 2 \). Do đoạn giới hạn là \( [0, 2] \), ta chỉ xét nghiệm \( x = 2 \).
Bước 2: Tính tích phân của hiệu các hàm số trên đoạn \( [0, 2] \).
Ta có:
\[
S = \int_{0}^{2} (x + 2 - x^2) \, dx
\]
Tính tích phân từng phần:
\[
S = \int_{0}^{2} x \, dx + \int_{0}^{2} 2 \, dx - \int_{0}^{2} x^2 \, dx
\]
Tính kết quả:
- \( \int_{0}^{2} x \, dx = \left[\frac{x^2}{2}\right]_{0}^{2} = 2 \)
- \( \int_{0}^{2} 2 \, dx = \left[2x\right]_{0}^{2} = 4 \)
- \( \int_{0}^{2} x^2 \, dx = \left[\frac{x^3}{3}\right]_{0}^{2} = \frac{8}{3} \)
Kết quả tổng diện tích:
\[
S = 2 + 4 - \frac{8}{3} = \frac{10}{3}
\]
Vậy, diện tích hình phẳng giữa hai đồ thị trên đoạn \( [0, 2] \) là \( \frac{10}{3} \) đơn vị diện tích.
Dạng bài 9: Dãy số và giới hạn
Trong toán học, dãy số và giới hạn là một phần quan trọng, đặc biệt trong các bài toán liên quan đến tính toán giới hạn của một dãy số. Hãy cùng tìm hiểu chi tiết các bước để giải một bài toán về dãy số và giới hạn.
Bước 1: Xác định dãy số
Trước hết, cần xác định công thức tổng quát của dãy số \( \{a_n\} \). Công thức này có thể được cho dưới dạng tổng quát hoặc dưới dạng đệ quy.
- Nếu dãy số được cho dưới dạng tổng quát: \( a_n = f(n) \), hãy ghi rõ công thức này và xác định tính chất của dãy số.
- Nếu dãy số được cho dưới dạng đệ quy: \( a_{n+1} = g(a_n) \), hãy xác định các phần tử đầu tiên của dãy số và tính toán các phần tử tiếp theo.
Bước 2: Tính giới hạn của dãy số
Giới hạn của dãy số \( \{a_n\} \) khi \( n \to \infty \) là một khái niệm quan trọng trong toán học. Ta cần thực hiện các bước sau để tính giới hạn:
- Giả sử dãy số \( \{a_n\} \) hội tụ đến giới hạn \( L \), tức là \( \lim_{{n \to \infty}} a_n = L \).
- Áp dụng các định lý và quy tắc giới hạn để tính \( L \). Chẳng hạn, nếu \( \lim_{{n \to \infty}} \frac{1}{n} = 0 \) thì ta có thể dùng quy tắc này để tính các giới hạn khác.
- Nếu dãy số có dạng đệ quy, hãy đặt \( \lim_{{n \to \infty}} a_n = L \) và giải phương trình để tìm \( L \).
- Kiểm tra tính hội tụ của dãy số, chẳng hạn bằng cách kiểm tra dấu hiệu của \( a_{n+1} - a_n \).
Ví dụ minh họa
Xét dãy số \( a_n = \frac{1}{n} \). Chúng ta sẽ tìm giới hạn của dãy số này khi \( n \to \infty \).
Ta có:
Vì \( \frac{1}{n} \) giảm dần và tiến dần đến 0 khi \( n \) tăng lên, do đó giới hạn của dãy số này là \( L = 0 \).
Bài tập tự luyện
Hãy thử giải bài toán sau:
- Tìm giới hạn của dãy số \( a_n = \frac{2n + 3}{n + 1} \) khi \( n \to \infty \).
- Giải dãy số đệ quy \( a_{n+1} = \frac{a_n + 1}{2} \) với \( a_1 = 2 \). Tìm giới hạn của dãy số này khi \( n \to \infty \).
Dạng bài 10: Tìm giá trị lớn nhất, nhỏ nhất của hàm số
Trong toán học, việc tìm giá trị lớn nhất và nhỏ nhất của một hàm số là một trong những bài toán cơ bản và quan trọng. Đây là những bước cơ bản để giải quyết dạng bài này:
- Định nghĩa hàm số:
Giả sử ta có một hàm số \( f(x) \) xác định trên một khoảng hoặc đoạn nào đó. Mục tiêu của chúng ta là tìm giá trị lớn nhất và nhỏ nhất của hàm số này trên đoạn hoặc khoảng đã cho.
- Tính đạo hàm của hàm số:
Đạo hàm của hàm số \( f(x) \), ký hiệu là \( f'(x) \), được sử dụng để xác định các điểm cực trị của hàm số. Cụ thể, ta cần giải phương trình \( f'(x) = 0 \) để tìm các điểm khả nghi.
- Xác định các điểm nghi ngờ:
Các điểm nghi ngờ để tìm giá trị lớn nhất và nhỏ nhất của hàm số bao gồm các điểm mà đạo hàm bằng 0 và các điểm biên của đoạn xác định.
- Tính giá trị hàm số tại các điểm nghi ngờ:
Tính giá trị của hàm số tại các điểm vừa tìm được ở bước trên. Cụ thể, ta cần tính \( f(x) \) tại các điểm này để so sánh và xác định giá trị lớn nhất và nhỏ nhất.
- So sánh giá trị:
So sánh các giá trị của hàm số \( f(x) \) tại các điểm vừa tính để tìm ra giá trị lớn nhất và nhỏ nhất của hàm số trên khoảng đã cho.
Ví dụ, xét hàm số \( f(x) = x^3 - 3x^2 + 4 \) trên đoạn \([0, 2]\).
- Bước 1: Tính đạo hàm \( f'(x) = 3x^2 - 6x \).
- Bước 2: Giải phương trình \( f'(x) = 0 \), ta có \( 3x(x - 2) = 0 \), suy ra \( x = 0 \) hoặc \( x = 2 \).
- Bước 3: Tính giá trị của hàm số tại các điểm \( x = 0 \), \( x = 2 \) và kiểm tra giá trị tại biên:
- \( f(0) = 4 \)
- \( f(2) = 4 \)
- Bước 4: So sánh các giá trị vừa tính được để xác định giá trị lớn nhất và nhỏ nhất. Trong trường hợp này, \( f(x) \) có giá trị lớn nhất và nhỏ nhất bằng 4.
Trên đây là cách tiếp cận cơ bản để tìm giá trị lớn nhất và nhỏ nhất của hàm số. Các bước này có thể áp dụng cho nhiều bài toán khác nhau trong các kỳ thi và ứng dụng thực tế.