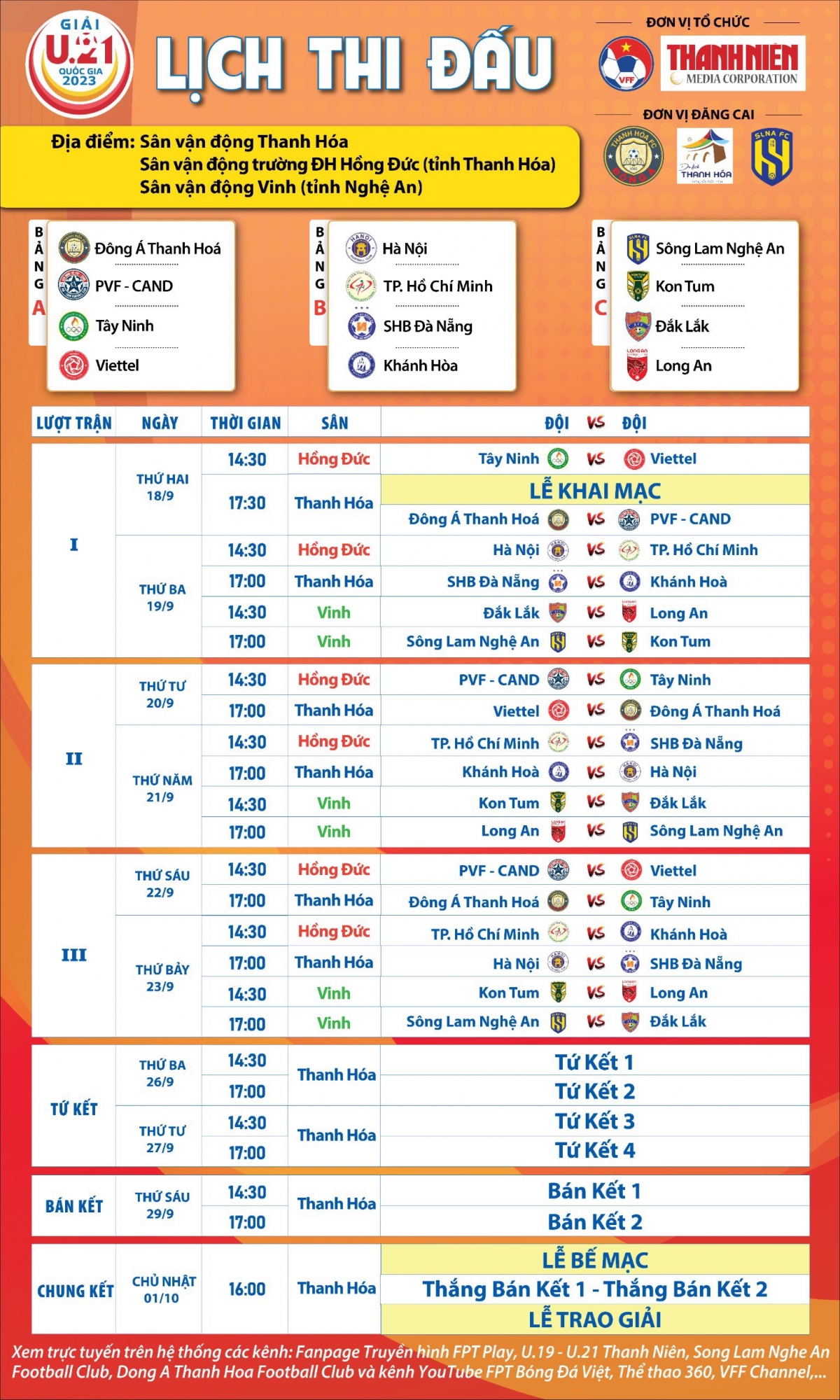
Chủ đề phần mềm tạo lịch thi đấu bóng đá: Phần mềm tạo lịch thi đấu bóng đá là công cụ không thể thiếu cho những ai tổ chức giải đấu từ phong trào đến chuyên nghiệp. Với tính năng lên lịch tự động, quản lý kết quả, và theo dõi xếp hạng, các phần mềm này giúp tối ưu hóa quá trình tổ chức và mang lại hiệu quả cao.
Mục lục
- Phần Mềm Tạo Lịch Thi Đấu Bóng Đá: Tổng Quan và Lựa Chọn Phổ Biến
- Mục Lục Tổng Hợp
- Dạng Bài Tập Toán Có Lời Giải
- Dạng Bài Tập Vật Lý Có Lời Giải
- Dạng Bài Tập Tiếng Anh Có Lời Giải
- 1. Tính toán thời gian di chuyển của một vật rơi tự do
- 2. Giải bài toán đường tròn ngoại tiếp và nội tiếp tam giác
- 3. Dạng bài tập sử dụng câu điều kiện loại 1, 2, 3 trong tiếng Anh
- 4. Dạng bài tập tính lực đẩy Ác-si-mét
- 5. Bài tập xác định số đo góc trong các hình học phẳng
- 6. Cách chia động từ bất quy tắc trong câu hỏi tiếng Anh
- 7. Bài tập tính vận tốc trung bình của một chuyển động thẳng
- 8. Dạng bài tập sử dụng mệnh đề quan hệ trong tiếng Anh
- 9. Bài tập tính quãng đường và thời gian di chuyển trong vật lý
- 10. Dạng bài tập xác định số lượng từ vựng tiếng Anh trong đoạn văn
Phần Mềm Tạo Lịch Thi Đấu Bóng Đá: Tổng Quan và Lựa Chọn Phổ Biến
Các phần mềm tạo lịch thi đấu bóng đá hiện đang là công cụ hữu ích cho việc tổ chức các giải đấu từ quy mô nhỏ đến chuyên nghiệp. Những phần mềm này giúp tự động hóa quy trình lên lịch, quản lý giải đấu và theo dõi kết quả một cách chính xác và hiệu quả.
Tính Năng Chung của Phần Mềm Tạo Lịch Thi Đấu Bóng Đá
- Tạo lịch thi đấu tự động với khả năng tùy chỉnh linh hoạt.
- Quản lý đội bóng và cầu thủ, bao gồm thông tin, xếp hạng và kết quả thi đấu.
- Hỗ trợ đa dạng thể loại giải đấu từ vòng bảng đến loại trực tiếp.
- Xuất bản báo cáo, biên bản trận đấu và bảng xếp hạng một cách nhanh chóng.
Một Số Phần Mềm Phổ Biến Hiện Nay
- Winner: Ứng dụng quản lý giải đấu trên Android với giao diện thân thiện, hỗ trợ nhiều bộ môn thể thao như bóng đá, tennis và bóng bàn. Người dùng có thể dễ dàng tạo giải đấu, cập nhật kết quả, và quản lý xếp hạng tự động.
- Pro-League: Công cụ quản lý giải đấu trực tuyến phù hợp cho các giải đấu phong trào, với tính năng sắp lịch thi đấu, quản lý đội bóng và thống kê chi tiết.
- FAGleague: Hệ thống quản lý giải đấu toàn diện, hỗ trợ từ việc bốc thăm, tạo lịch, đến quản lý truyền thông và tài trợ. Phần mềm này được nhiều tổ chức sử dụng nhờ khả năng tùy chỉnh cao.
- Vtranet: Phần mềm được tùy biến riêng cho từng giải đấu, đặc biệt phù hợp với các sự kiện thể thao quy mô lớn như ASEAN Games.
Lợi Ích Khi Sử Dụng Phần Mềm Quản Lý Giải Đấu
Việc áp dụng phần mềm vào quản lý giải đấu giúp tăng tính chính xác, tiết kiệm thời gian và cải thiện hiệu quả công việc. Người tổ chức có thể theo dõi toàn bộ tiến trình giải đấu, từ lịch thi đấu, kết quả đến quản lý tài chính, nhờ đó giảm thiểu rủi ro và tối ưu hóa quá trình tổ chức.
Hướng Dẫn Sử Dụng và Triển Khai
- Đăng ký và thiết lập giải đấu thông qua giao diện phần mềm, bao gồm thông tin đội bóng, quy tắc xếp hạng và cấu hình lịch thi đấu.
- Hệ thống tự động lên lịch dựa trên cấu hình và mã đội, cho phép điều chỉnh chi tiết về thời gian và sân đấu.
- Cập nhật kết quả, quản lý bảng xếp hạng và xuất bản biên bản trận đấu một cách dễ dàng.
.png)
Mục Lục Tổng Hợp
1. Giới thiệu về phần mềm tạo lịch thi đấu bóng đá
- Phần mềm tạo lịch thi đấu là gì?
- Lợi ích của việc sử dụng phần mềm trong tổ chức giải đấu
2. Các tính năng chính của phần mềm tạo lịch thi đấu bóng đá
- Lên lịch tự động và tùy chỉnh
- Quản lý đội bóng, cầu thủ và thông tin chi tiết
- Tự động cập nhật kết quả và xếp hạng
- Xuất bản báo cáo và biên bản trận đấu
3. Hướng dẫn sử dụng phần mềm tạo lịch thi đấu
- Cách thiết lập giải đấu và cấu hình lịch thi đấu
- Cách quản lý đội bóng và thông tin cầu thủ
- Hướng dẫn xuất dữ liệu và báo cáo
4. Phân tích các phần mềm tạo lịch thi đấu phổ biến
- Winner - Phần mềm trên Android dành cho các giải đấu phong trào
- FAGleague - Hệ thống quản lý giải đấu chuyên nghiệp
- Vtranet - Phần mềm tùy biến cho các giải đấu quy mô lớn
5. Cách chọn phần mềm tạo lịch thi đấu phù hợp
- So sánh phần mềm miễn phí và có phí
- Đánh giá dựa trên nhu cầu sử dụng và quy mô giải đấu
6. Top 5 phần mềm tạo lịch thi đấu bóng đá tốt nhất hiện nay
- Danh sách các phần mềm phổ biến và uy tín
- Ưu và nhược điểm của từng phần mềm
7. Cách tùy chỉnh lịch thi đấu và xếp hạng
- Hướng dẫn điều chỉnh lịch thi đấu theo nhu cầu
- Tính năng xếp hạng dựa trên các tiêu chí khác nhau
8. Tính năng bổ sung và cập nhật mới của phần mềm
- Quản lý truyền thông và tài trợ
- Tích hợp các báo cáo nâng cao và phân tích dữ liệu
9. Các lưu ý khi sử dụng phần mềm tạo lịch thi đấu bóng đá
- Những sai lầm thường gặp và cách khắc phục
- Cách bảo mật thông tin và dữ liệu giải đấu
10. Tương lai của phần mềm tạo lịch thi đấu bóng đá
- Xu hướng phát triển và ứng dụng công nghệ mới
- Tích hợp AI và tự động hóa trong quản lý giải đấu
Dạng Bài Tập Toán Có Lời Giải
Bài tập 1: Giải phương trình bậc hai
Giải phương trình \( ax^2 + bx + c = 0 \) với \( a = 2 \), \( b = -5 \), và \( c = 3 \).
Lời giải:
Sử dụng công thức nghiệm:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]Thay các giá trị vào:
\[ x = \frac{5 \pm \sqrt{(-5)^2 - 4 \times 2 \times 3}}{2 \times 2} = \frac{5 \pm \sqrt{25 - 24}}{4} = \frac{5 \pm 1}{4} \]Vậy nghiệm của phương trình là \( x = 1.5 \) và \( x = 1 \).
Bài tập 2: Tính diện tích tam giác
Cho tam giác có độ dài ba cạnh là \( a = 3 \), \( b = 4 \), và \( c = 5 \). Tính diện tích của tam giác.
Lời giải:
Sử dụng công thức Heron:
\[ S = \sqrt{s(s - a)(s - b)(s - c)} \]Với \( s = \frac{a + b + c}{2} = \frac{3 + 4 + 5}{2} = 6 \).
Thay vào công thức:
\[ S = \sqrt{6(6 - 3)(6 - 4)(6 - 5)} = \sqrt{6 \times 3 \times 2 \times 1} = \sqrt{36} = 6 \]Vậy diện tích của tam giác là \( 6 \) đơn vị diện tích.
Bài tập 3: Tính chu vi hình tròn
Cho hình tròn có bán kính \( r = 7 \). Tính chu vi của hình tròn.
Lời giải:
Chu vi hình tròn được tính theo công thức:
\[ C = 2\pi r \]Thay giá trị \( r \) vào:
\[ C = 2\pi \times 7 = 14\pi \approx 43.96 \]Vậy chu vi của hình tròn là \( 43.96 \) đơn vị chiều dài.
Bài tập 4: Giải hệ phương trình bậc nhất hai ẩn
Giải hệ phương trình sau:
\[ \begin{cases} 2x + 3y = 7 \\ 4x - y = 1 \end{cases} \]Lời giải:
Giải bằng phương pháp thế:
Từ phương trình thứ hai, ta có:
\[ y = 4x - 1 \]Thay vào phương trình thứ nhất:
\[ 2x + 3(4x - 1) = 7 \Rightarrow 2x + 12x - 3 = 7 \Rightarrow 14x = 10 \Rightarrow x = \frac{5}{7} \]Thay \( x = \frac{5}{7} \) vào \( y = 4x - 1 \), ta có:
\[ y = 4 \times \frac{5}{7} - 1 = \frac{20}{7} - \frac{7}{7} = \frac{13}{7} \]Vậy nghiệm của hệ phương trình là \( x = \frac{5}{7} \) và \( y = \frac{13}{7} \).
Bài tập 5: Tính tổng của dãy số
Tính tổng của dãy số \( 1 + 2 + 3 + \dots + 100 \).
Lời giải:
Sử dụng công thức tính tổng của cấp số cộng:
\[ S = \frac{n(a_1 + a_n)}{2} \]Với \( n = 100 \), \( a_1 = 1 \), và \( a_n = 100 \), ta có:
\[ S = \frac{100(1 + 100)}{2} = 5050 \]Vậy tổng của dãy số là \( 5050 \).

Dạng Bài Tập Vật Lý Có Lời Giải
Bài tập 1: Tính vận tốc trong chuyển động thẳng đều
Một xe ô tô đi từ điểm A đến điểm B với quãng đường \( s = 120 \, km \) trong thời gian \( t = 2 \, h \). Tính vận tốc của xe.
Lời giải:
Vận tốc trong chuyển động thẳng đều được tính theo công thức:
\[ v = \frac{s}{t} \]Thay các giá trị vào:
\[ v = \frac{120}{2} = 60 \, km/h \]Vậy vận tốc của xe là \( 60 \, km/h \).
Bài tập 2: Tính quãng đường trong chuyển động thẳng biến đổi đều
Một vật chuyển động thẳng nhanh dần đều với vận tốc ban đầu \( v_0 = 5 \, m/s \) và gia tốc \( a = 2 \, m/s^2 \). Tính quãng đường vật đi được trong \( t = 4 \, s \).
Lời giải:
Quãng đường trong chuyển động thẳng nhanh dần đều được tính theo công thức:
\[ s = v_0t + \frac{1}{2}at^2 \]Thay các giá trị vào:
\[ s = 5 \times 4 + \frac{1}{2} \times 2 \times 4^2 = 20 + 16 = 36 \, m \]Vậy quãng đường vật đi được là \( 36 \, m \).
Bài tập 3: Tính lực đẩy Ác-si-mét
Một vật có thể tích \( V = 0.05 \, m^3 \) được nhúng chìm hoàn toàn trong nước. Biết trọng lượng riêng của nước là \( d = 10000 \, N/m^3 \). Tính lực đẩy Ác-si-mét tác dụng lên vật.
Lời giải:
Lực đẩy Ác-si-mét được tính theo công thức:
\[ F = dV \]Thay các giá trị vào:
\[ F = 10000 \times 0.05 = 500 \, N \]Vậy lực đẩy Ác-si-mét tác dụng lên vật là \( 500 \, N \).
Bài tập 4: Tính công suất tiêu thụ của một thiết bị điện
Một bóng đèn có hiệu điện thế \( U = 220 \, V \) và cường độ dòng điện \( I = 0.5 \, A \). Tính công suất tiêu thụ của bóng đèn.
Lời giải:
Công suất tiêu thụ của thiết bị điện được tính theo công thức:
\[ P = UI \]Thay các giá trị vào:
\[ P = 220 \times 0.5 = 110 \, W \]Vậy công suất tiêu thụ của bóng đèn là \( 110 \, W \).
Bài tập 5: Tính độ lớn lực ma sát
Một vật có khối lượng \( m = 10 \, kg \) nằm trên mặt phẳng ngang. Hệ số ma sát giữa vật và mặt phẳng là \( \mu = 0.2 \). Tính lực ma sát tác dụng lên vật.
Lời giải:
Lực ma sát được tính theo công thức:
\[ F_{ms} = \mu mg \]Với \( g = 9.8 \, m/s^2 \), ta có:
\[ F_{ms} = 0.2 \times 10 \times 9.8 = 19.6 \, N \]Vậy lực ma sát tác dụng lên vật là \( 19.6 \, N \).
Dạng Bài Tập Tiếng Anh Có Lời Giải
Bài tập 1: Chia động từ trong ngoặc
Hoàn thành câu sau bằng cách chia động từ trong ngoặc:
1. She usually (go) ______ to school by bus.
2. I (be) ______ at the supermarket yesterday.
Lời giải:
1. She usually goes to school by bus.
2. I was at the supermarket yesterday.
Bài tập 2: Điền giới từ thích hợp
Điền giới từ phù hợp vào chỗ trống:
1. She is interested ______ learning languages.
2. The cat is hiding ______ the table.
Lời giải:
1. She is interested in learning languages.
2. The cat is hiding under the table.
Bài tập 3: Viết lại câu sử dụng từ gợi ý
Viết lại câu sau sử dụng từ gợi ý trong ngoặc:
1. She is taller than me. (short)
2. They can’t play football because of the rain. (if)
Lời giải:
1. I am shorter than her.
2. If it weren’t for the rain, they could play football.
Bài tập 4: Điền từ vào chỗ trống
Điền từ phù hợp vào chỗ trống để hoàn thành đoạn văn sau:
My family and I (1) ______ going to the zoo next Sunday. We plan to (2) ______ a lot of animals.
Lời giải:
1. are
2. see
Bài tập 5: Chọn từ đồng nghĩa
Chọn từ đồng nghĩa với từ in đậm:
1. The movie was fantastic.
a) awful b) wonderful c) boring
2. She was angry about the delay.
a) pleased b) furious c) calm
Lời giải:
1. b) wonderful
2. b) furious

1. Tính toán thời gian di chuyển của một vật rơi tự do
Khi một vật rơi tự do từ độ cao \( h \) xuống mặt đất, thời gian di chuyển của vật có thể được tính dựa trên công thức:
Trong đó:
- \( t \) là thời gian di chuyển (tính bằng giây, \( s \)).
- \( h \) là độ cao ban đầu của vật (tính bằng mét, \( m \)).
- \( g \) là gia tốc trọng trường (khoảng \( 9.8 \, m/s^2 \) trên Trái Đất).
Ví dụ:
Một vật rơi tự do từ độ cao \( h = 20 \, m \). Tính thời gian vật chạm đất.
Lời giải:
Thay số vào công thức:
Vậy thời gian vật chạm đất là khoảng \( 2.02 \, s \).
Như vậy, công thức tính toán thời gian rơi tự do là một ứng dụng quan trọng trong vật lý, đặc biệt hữu ích trong việc giải quyết các bài toán liên quan đến chuyển động dưới tác dụng của trọng lực.
XEM THÊM:
2. Giải bài toán đường tròn ngoại tiếp và nội tiếp tam giác
Trong hình học, việc xác định đường tròn ngoại tiếp và nội tiếp của một tam giác là một bài toán phổ biến và quan trọng. Bài toán này giúp chúng ta hiểu rõ hơn về tính chất hình học của tam giác và các đường tròn liên quan. Dưới đây là hướng dẫn chi tiết để giải bài toán này.
Bước 1: Xác định đường tròn ngoại tiếp tam giác
- Xác định trung điểm của các cạnh tam giác: Để bắt đầu, hãy xác định trung điểm của mỗi cạnh tam giác. Giả sử tam giác có ba đỉnh \( A(x_1, y_1) \), \( B(x_2, y_2) \), và \( C(x_3, y_3) \). Trung điểm của các cạnh sẽ lần lượt là: \[ M_{AB} = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) \] \[ M_{BC} = \left(\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}\right) \] \[ M_{CA} = \left(\frac{x_3 + x_1}{2}, \frac{y_3 + y_1}{2}\right) \]
- Vẽ đường trung trực của các cạnh: Đường trung trực của mỗi cạnh là đường thẳng đi qua trung điểm của cạnh đó và vuông góc với cạnh. Để xác định phương trình đường trung trực, sử dụng phương trình đường thẳng với hệ số góc nghịch đảo của hệ số góc của cạnh tương ứng.
- Xác định tâm của đường tròn ngoại tiếp: Tâm của đường tròn ngoại tiếp chính là giao điểm của ba đường trung trực vừa vẽ. Giao điểm này là điểm cách đều ba đỉnh của tam giác.
- Tính bán kính đường tròn ngoại tiếp: Bán kính \( R \) của đường tròn ngoại tiếp được tính bằng khoảng cách từ tâm đường tròn đến bất kỳ đỉnh nào của tam giác. Công thức tính bán kính là: \[ R = \frac{abc}{4S} \] Trong đó \( a, b, c \) là độ dài các cạnh của tam giác, và \( S \) là diện tích tam giác, có thể được tính bằng công thức Heron: \[ S = \sqrt{p(p-a)(p-b)(p-c)} \] với \( p \) là nửa chu vi tam giác.
Bước 2: Xác định đường tròn nội tiếp tam giác
- Xác định các đường phân giác của tam giác: Đường phân giác của một góc trong tam giác là đường thẳng chia góc đó thành hai góc bằng nhau. Để xác định đường phân giác, sử dụng công thức lượng giác hoặc hình học cơ bản.
- Xác định tâm của đường tròn nội tiếp: Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác. Điểm này cũng chính là điểm cách đều ba cạnh của tam giác.
- Tính bán kính đường tròn nội tiếp: Bán kính \( r \) của đường tròn nội tiếp được tính bằng công thức: \[ r = \frac{S}{p} \] với \( S \) là diện tích tam giác và \( p \) là nửa chu vi tam giác.
Qua các bước trên, chúng ta có thể xác định được cả đường tròn ngoại tiếp và nội tiếp của tam giác. Việc hiểu rõ các bước giải này sẽ giúp bạn nắm vững kiến thức về hình học phẳng và ứng dụng chúng trong nhiều bài toán khác nhau.

3. Dạng bài tập sử dụng câu điều kiện loại 1, 2, 3 trong tiếng Anh
Câu điều kiện là một cấu trúc ngữ pháp quan trọng trong tiếng Anh, thường được dùng để diễn tả giả định về một tình huống nào đó. Có ba loại câu điều kiện chính:
- Câu điều kiện loại 1: Dùng để diễn tả một sự việc có thể xảy ra trong tương lai.
- Câu điều kiện loại 2: Dùng để diễn tả một sự việc không có thật ở hiện tại hoặc giả định.
- Câu điều kiện loại 3: Dùng để diễn tả một sự việc không có thật trong quá khứ và hậu quả của nó.
Dưới đây là hướng dẫn chi tiết từng bước để giải các bài tập sử dụng câu điều kiện loại 1, 2, 3:
1. Câu điều kiện loại 1
Cấu trúc: If + S + V(hiện tại đơn), S + will + V(nguyên thể)
- Bước 1: Xác định mệnh đề điều kiện và mệnh đề kết quả.
- Bước 2: Chia động từ trong mệnh đề điều kiện ở thì hiện tại đơn.
- Bước 3: Sử dụng “will” cộng với động từ nguyên thể trong mệnh đề kết quả.
- Ví dụ: If it rains tomorrow, we will stay at home.
2. Câu điều kiện loại 2
Cấu trúc: If + S + V(quá khứ đơn), S + would + V(nguyên thể)
- Bước 1: Xác định mệnh đề điều kiện và mệnh đề kết quả.
- Bước 2: Chia động từ trong mệnh đề điều kiện ở thì quá khứ đơn.
- Bước 3: Sử dụng “would” cộng với động từ nguyên thể trong mệnh đề kết quả.
- Ví dụ: If I had a lot of money, I would travel around the world.
3. Câu điều kiện loại 3
Cấu trúc: If + S + had + V(pp), S + would have + V(pp)
- Bước 1: Xác định mệnh đề điều kiện và mệnh đề kết quả.
- Bước 2: Chia động từ trong mệnh đề điều kiện ở thì quá khứ hoàn thành.
- Bước 3: Sử dụng “would have” cộng với động từ phân từ hai trong mệnh đề kết quả.
- Ví dụ: If she had studied harder, she would have passed the exam.
Hãy thực hành các dạng bài tập này để làm quen và hiểu rõ hơn về cách sử dụng câu điều kiện trong tiếng Anh. Chúng không chỉ giúp bạn cải thiện ngữ pháp mà còn làm phong phú thêm vốn từ vựng của bạn.

4. Dạng bài tập tính lực đẩy Ác-si-mét
Trong bài toán về lực đẩy Ác-si-mét, chúng ta cần tìm hiểu cách tính toán lực đẩy mà một vật phải chịu khi được đặt vào trong chất lỏng. Lực đẩy này có thể được tính dựa trên công thức của Ác-si-mét:
Trong đó:
- \(F_A\) là lực đẩy Ác-si-mét (N).
- \(\rho\) là khối lượng riêng của chất lỏng (kg/m³).
- \(V\) là thể tích phần chất lỏng bị chiếm chỗ bởi vật (m³).
- \(g\) là gia tốc trọng trường, thường lấy giá trị là 9.8 m/s².
Ví dụ:
Giả sử chúng ta có một khối gỗ hình hộp chữ nhật có thể tích \(V = 0.5\) m³ được thả nổi trong nước. Biết khối lượng riêng của nước là \(\rho = 1000\) kg/m³, ta tính lực đẩy Ác-si-mét mà khối gỗ này chịu như sau:
Bước 1: Xác định các giá trị cần thiết, bao gồm khối lượng riêng của chất lỏng và thể tích vật.
Bước 2: Áp dụng công thức \(F_A = \rho \cdot V \cdot g\) để tính toán lực đẩy.
Bước 3: Kiểm tra và xác nhận kết quả để đảm bảo tính toán chính xác.
Qua ví dụ trên, chúng ta thấy rằng lực đẩy Ác-si-mét phụ thuộc trực tiếp vào khối lượng riêng của chất lỏng và thể tích của vật chìm trong chất lỏng. Khi vật có thể tích lớn hơn hoặc chất lỏng có khối lượng riêng lớn hơn, lực đẩy sẽ tăng lên.
Hãy thực hành thêm nhiều bài tập khác để nắm vững cách tính lực đẩy Ác-si-mét trong các tình huống khác nhau.
5. Bài tập xác định số đo góc trong các hình học phẳng
Bài tập xác định số đo góc trong hình học phẳng là một phần quan trọng trong việc hiểu và áp dụng các kiến thức toán học. Dưới đây là hướng dẫn chi tiết từng bước để giải quyết dạng bài tập này.
Bước 1: Xác định loại tam giác và các tính chất liên quan
Trước tiên, bạn cần xác định loại tam giác (cân, đều, vuông, thường) vì mỗi loại có những tính chất riêng biệt về góc mà bạn có thể sử dụng:
- Tam giác đều: Mỗi góc đều bằng \(60^\circ\).
- Tam giác vuông: Một góc bằng \(90^\circ\), hai góc còn lại phụ nhau.
- Tam giác cân: Hai góc bằng nhau và góc còn lại được tính bằng \(180^\circ\) trừ đi hai góc đó.
Bước 2: Sử dụng định lý tổng các góc trong tam giác
Tổng ba góc trong một tam giác luôn bằng \(180^\circ\). Đây là cơ sở để tính toán khi đã biết hai trong ba góc:
\[ \text{Góc còn lại} = 180^\circ - \text{(Góc 1 + Góc 2)} \]
Bước 3: Áp dụng các định lý hình học khác (nếu cần)
Trong một số bài toán phức tạp hơn, bạn có thể cần sử dụng các định lý sau:
- Định lý Sin: \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\) giúp bạn xác định góc khi biết các cạnh.
- Định lý Cosin: \(c^2 = a^2 + b^2 - 2ab \cdot \cos C\) để tìm góc khi biết ba cạnh.
Bước 4: Giải bài toán cụ thể
Ví dụ, cho tam giác ABC với các góc A, B, và C:
- Giả sử biết góc A và B, bạn tính được góc C: \[ C = 180^\circ - (A + B) \]
- Nếu biết hai cạnh và một góc giữa chúng, sử dụng định lý Cosin để tìm góc còn lại.
- Trong trường hợp biết một góc và hai cạnh kề, áp dụng định lý Sin để xác định các góc còn lại.
Kết luận
Bằng cách áp dụng các bước và công thức nêu trên, bạn sẽ có thể giải quyết bất kỳ bài toán nào liên quan đến việc xác định số đo góc trong các hình học phẳng.

6. Cách chia động từ bất quy tắc trong câu hỏi tiếng Anh
Trong tiếng Anh, động từ bất quy tắc là những động từ không tuân theo quy tắc chung của việc thêm "-ed" ở cuối để tạo dạng quá khứ và quá khứ phân từ. Việc chia động từ bất quy tắc trong câu hỏi tiếng Anh yêu cầu bạn phải nắm vững các dạng của động từ này.
Dưới đây là hướng dẫn chi tiết cách chia động từ bất quy tắc trong các câu hỏi:
-
Câu hỏi với động từ "to be":
Trong các câu hỏi sử dụng động từ "to be", bạn chỉ cần đảo ngược vị trí của động từ và chủ ngữ. Ví dụ:
- Hiện tại đơn: Are you happy?
- Quá khứ đơn: Were they at the party?
-
Câu hỏi với động từ thường:
Khi tạo câu hỏi với động từ thường, bạn cần sử dụng trợ động từ "do/does" cho hiện tại đơn và "did" cho quá khứ đơn:
- Hiện tại đơn: Do you go to school every day?
- Quá khứ đơn: Did she write a letter?
-
Câu hỏi với động từ bất quy tắc:
Trong quá khứ đơn, các động từ bất quy tắc không thêm "-ed" mà có dạng riêng biệt. Khi tạo câu hỏi, bạn vẫn sử dụng "did" nhưng động từ chính quay về dạng nguyên mẫu:
- Ví dụ: Did you eat breakfast? (Động từ chính "eat" không thêm "-ed").
-
Bài tập thực hành:
- Chia động từ "go" trong câu hỏi: ____ you ____ to the cinema last night?
Đáp án: Did you go to the cinema last night?
- Chia động từ "see" trong câu hỏi: ____ she ____ the movie?
Đáp án: Did she see the movie?
- Chia động từ "be" trong câu hỏi: ____ they ____ at home yesterday?
Đáp án: Were they at home yesterday?
- Chia động từ "go" trong câu hỏi: ____ you ____ to the cinema last night?
7. Bài tập tính vận tốc trung bình của một chuyển động thẳng
Trong bài tập này, chúng ta sẽ cùng nhau tính toán vận tốc trung bình của một chuyển động thẳng. Vận tốc trung bình được định nghĩa là tỷ số giữa tổng quãng đường đi được và tổng thời gian di chuyển.
Công thức tính vận tốc trung bình:
\[
v_{tb} = \frac{S_{total}}{t_{total}}
\]
Trong đó:
- \(v_{tb}\) là vận tốc trung bình (m/s).
- \(S_{total}\) là tổng quãng đường đi được (m).
- \(t_{total}\) là tổng thời gian di chuyển (s).
Ví dụ 1:
Một ô tô di chuyển trên đoạn đường thẳng từ A đến B với quãng đường là 120 km trong 2 giờ, sau đó tiếp tục di chuyển từ B đến C với quãng đường 60 km trong 1 giờ. Hãy tính vận tốc trung bình của ô tô trên cả đoạn đường từ A đến C.
Bước 1: Tính tổng quãng đường \(S_{total}\).
\[
S_{total} = 120\,km + 60\,km = 180\,km
\]
Bước 2: Tính tổng thời gian di chuyển \(t_{total}\).
\[
t_{total} = 2\,hours + 1\,hour = 3\,hours
\]
Bước 3: Áp dụng công thức tính vận tốc trung bình:
\[
v_{tb} = \frac{180\,km}{3\,hours} = 60\,km/h
\]
Vậy vận tốc trung bình của ô tô trên cả đoạn đường là 60 km/h.
Bài tập thực hành:
- Một người đi bộ trên một đoạn đường thẳng dài 6 km trong 1,5 giờ. Tính vận tốc trung bình của người đó.
- Một xe máy di chuyển trên đoạn đường 90 km trong 1,5 giờ, sau đó di chuyển thêm 30 km trong 0,5 giờ. Tính vận tốc trung bình của xe máy trên toàn bộ đoạn đường.
- Một chiếc tàu di chuyển trên đoạn đường 300 km trong 4 giờ. Sau đó, nó tiếp tục di chuyển thêm 200 km trong 3 giờ. Tính vận tốc trung bình của tàu trên toàn bộ hành trình.
8. Dạng bài tập sử dụng mệnh đề quan hệ trong tiếng Anh
Mệnh đề quan hệ (relative clause) là một phần quan trọng trong tiếng Anh, giúp chúng ta bổ sung thông tin cho danh từ mà không cần phải bắt đầu một câu mới. Dưới đây là hướng dẫn chi tiết về cách sử dụng mệnh đề quan hệ, kèm theo các bài tập thực hành.
1. Khái niệm mệnh đề quan hệ
Mệnh đề quan hệ là mệnh đề phụ dùng để bổ sung ý nghĩa cho danh từ đứng trước nó, giúp câu rõ ràng và chính xác hơn. Mệnh đề quan hệ thường bắt đầu bằng các đại từ quan hệ như who, whom, whose, which, that.
2. Phân loại mệnh đề quan hệ
- Mệnh đề quan hệ xác định (Defining Relative Clause): Cung cấp thông tin cần thiết để hiểu đúng về danh từ. Ví dụ: The man who is standing over there is my uncle.
- Mệnh đề quan hệ không xác định (Non-defining Relative Clause): Bổ sung thông tin cho danh từ nhưng không cần thiết để hiểu ý nghĩa chính. Ví dụ: My uncle, who lives in London, is visiting us.
3. Cách sử dụng các đại từ quan hệ
- Who: Dùng để chỉ người làm chủ ngữ. Ví dụ: The teacher who teaches us is very kind.
- Whom: Dùng để chỉ người làm tân ngữ. Ví dụ: The girl whom I met yesterday is my friend.
- Which: Dùng để chỉ vật, sự việc. Ví dụ: The book which I am reading is interesting.
- Whose: Dùng để chỉ sự sở hữu. Ví dụ: The man whose car is parked outside is my neighbor.
- That: Có thể dùng thay thế cho who hoặc which trong mệnh đề xác định. Ví dụ: The dress that she bought is beautiful.
4. Bài tập thực hành
Dưới đây là một số bài tập để bạn thực hành việc sử dụng mệnh đề quan hệ:
- Điền từ thích hợp (who, whom, whose, which, that) vào chỗ trống:
This is the book _____ I told you about. - Kết hợp hai câu thành một câu có sử dụng mệnh đề quan hệ:
The man is my uncle. He is standing over there. - Viết lại câu với mệnh đề quan hệ không xác định:
My friend John is coming to visit. He lives in New York.
Hãy thực hành những bài tập trên để nắm vững cách sử dụng mệnh đề quan hệ trong tiếng Anh. Việc thành thạo cấu trúc này sẽ giúp bạn giao tiếp và viết tiếng Anh chính xác hơn.

9. Bài tập tính quãng đường và thời gian di chuyển trong vật lý
Trong vật lý, việc tính toán quãng đường và thời gian di chuyển là một kỹ năng cơ bản nhưng rất quan trọng. Để giải quyết các bài tập này, bạn cần hiểu rõ các công thức liên quan đến vận tốc, quãng đường và thời gian. Dưới đây là hướng dẫn chi tiết:
Bước 1: Xác định các đại lượng cơ bản
Trước hết, bạn cần xác định các đại lượng cơ bản có trong bài toán như vận tốc (\(v\)), quãng đường (\(s\)), và thời gian (\(t\)). Các công thức chính cần nhớ là:
- Vận tốc: \( v = \frac{s}{t} \)
- Quãng đường: \( s = v \times t \)
- Thời gian: \( t = \frac{s}{v} \)
Bước 2: Áp dụng công thức vào bài toán
Hãy bắt đầu với việc đọc kỹ đề bài và xác định xem những thông tin nào đã có và những gì cần tìm. Ví dụ, nếu đề bài cho vận tốc và thời gian, bạn sẽ sử dụng công thức tính quãng đường:
\[ s = v \times t \]
Nếu đề bài cung cấp quãng đường và vận tốc, bạn sẽ tính thời gian bằng cách:
\[ t = \frac{s}{v} \]
Bước 3: Giải các bài toán mẫu
-
Bài toán 1: Một ô tô di chuyển với vận tốc 60 km/h trong 2 giờ. Hãy tính quãng đường mà ô tô đã di chuyển.
Giải:
Áp dụng công thức tính quãng đường:
\[ s = v \times t = 60 \times 2 = 120 \text{ km} \]
Vậy ô tô đã di chuyển được 120 km.
-
Bài toán 2: Một người đi bộ với vận tốc 5 km/h và di chuyển quãng đường 15 km. Hãy tính thời gian người đó di chuyển.
Giải:
Áp dụng công thức tính thời gian:
\[ t = \frac{s}{v} = \frac{15}{5} = 3 \text{ giờ} \]
Vậy người đó đã di chuyển trong 3 giờ.
Bước 4: Thực hành thêm với các bài tập khác
Để thành thạo, bạn nên thực hành nhiều bài tập với các dạng đề khác nhau. Điều này giúp củng cố kiến thức và rèn luyện kỹ năng giải bài toán tính quãng đường và thời gian di chuyển.
10. Dạng bài tập xác định số lượng từ vựng tiếng Anh trong đoạn văn
Dạng bài tập xác định số lượng từ vựng tiếng Anh trong một đoạn văn thường xuất hiện trong các kỳ thi và bài kiểm tra năng lực ngôn ngữ. Để làm tốt dạng bài này, người học cần nắm rõ các bước sau:
- Đọc kỹ đoạn văn:
Trước tiên, hãy đọc đoạn văn một cách chậm rãi và cẩn thận. Mục tiêu là nắm bắt được nội dung chính của đoạn văn và nhận diện các từ vựng có thể xuất hiện nhiều lần.
- Xác định các từ loại:
Trong tiếng Anh, từ vựng có thể thuộc nhiều loại từ khác nhau như danh từ, động từ, tính từ, trạng từ. Hãy cố gắng phân loại các từ này để có thể xác định chính xác số lượng từ thuộc từng nhóm.
- Đếm từ:
Sau khi đã phân loại từ, bước tiếp theo là đếm số lượng từ trong đoạn văn. Lưu ý rằng một số từ có thể xuất hiện nhiều lần nhưng chỉ tính là một từ duy nhất nếu yêu cầu của bài tập là như vậy.
- Sử dụng công cụ hỗ trợ:
Nếu bài tập cho phép, bạn có thể sử dụng các công cụ như từ điển trực tuyến hoặc phần mềm đếm từ để hỗ trợ việc xác định số lượng từ một cách chính xác hơn.
- Kiểm tra lại:
Sau khi đã hoàn thành việc đếm từ, hãy kiểm tra lại kết quả của mình. Đảm bảo rằng bạn không bỏ sót bất kỳ từ nào hoặc đếm sai số lượng từ.
Với những bước hướng dẫn chi tiết như trên, người học có thể tự tin hơn khi thực hiện các bài tập xác định số lượng từ vựng trong đoạn văn tiếng Anh, đảm bảo kết quả chính xác và hiệu quả.