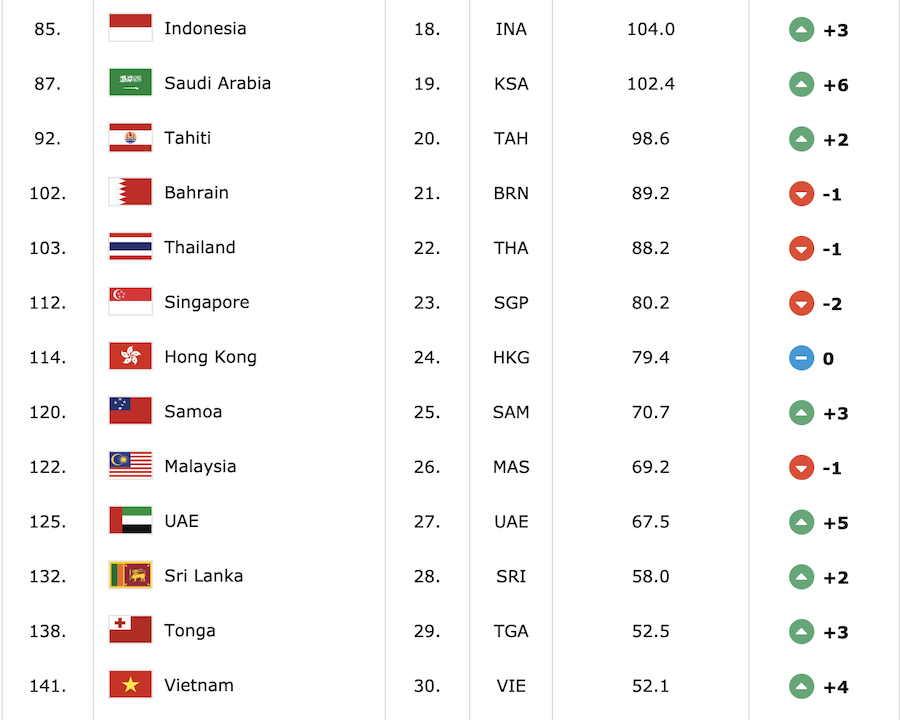
Chủ đề quần áo bóng rổ nam: Quần áo bóng rổ nam đang trở thành lựa chọn thời trang không thể thiếu cho giới trẻ yêu thích thể thao. Bài viết này sẽ khám phá các xu hướng mới nhất, cách chọn lựa sản phẩm phù hợp, và những thương hiệu uy tín tại Việt Nam, giúp bạn tự tin tỏa sáng trên sân đấu và trong cuộc sống hàng ngày.
Mục lục
- Thông Tin Về Quần Áo Bóng Rổ Nam Tại Việt Nam
- Mục Lục Tổng Hợp Về Quần Áo Bóng Rổ Nam
- 10 Dạng Bài Tập Toán Có Lời Giải Hoàn Chỉnh
- Bài Tập 1: Phân Tích Đa Thức Thành Nhân Tử
- Bài Tập 2: Giải Phương Trình Bậc Hai
- Bài Tập 3: Tính Giá Trị Biểu Thức Đại Số
- Bài Tập 4: Định Lý Py-ta-go
- Bài Tập 5: Ứng Dụng Đạo Hàm Trong Tính Toán Cực Trị
- Bài Tập 6: Tính Tích Phân Xác Định
- Bài Tập 7: Giải Hệ Phương Trình Tuyến Tính
- Bài Tập 8: Tính Diện Tích Và Chu Vi Hình Học Phẳng
- Bài Tập 9: Giải Bất Phương Trình
- Bài Tập 10: Tìm Giá Trị Lớn Nhất Và Nhỏ Nhất Của Hàm Số
Thông Tin Về Quần Áo Bóng Rổ Nam Tại Việt Nam
Quần áo bóng rổ nam tại Việt Nam đang trở thành xu hướng được nhiều người ưa chuộng, đặc biệt là giới trẻ. Các sản phẩm quần áo bóng rổ nam không chỉ phục vụ cho hoạt động thể thao mà còn mang tính thời trang cao, phù hợp với phong cách sống năng động.
Các Thương Hiệu Và Nhà Cung Cấp Nổi Bật
- Supersports Vietnam: Chuyên cung cấp quần áo bóng rổ chính hãng từ các thương hiệu nổi tiếng như Nike, Under Armour, với nhiều chương trình khuyến mãi hấp dẫn. Các sản phẩm tại đây thường có chất lượng cao và được bảo hành chính hãng.
- Sport1: Hệ thống cửa hàng thể thao với nhiều chi nhánh trên toàn quốc, cung cấp đa dạng các sản phẩm từ quần áo bóng rổ đến phụ kiện thể thao. Sport1 nổi tiếng với dịch vụ chăm sóc khách hàng tận tình và các chương trình ưu đãi đặc biệt cho khách hàng thân thiết.
- ARESSport: Đây là địa chỉ tin cậy cho những ai muốn đặt hàng quần áo bóng rổ thiết kế theo yêu cầu. ARESSport được biết đến với các sản phẩm độc đáo, chất liệu vải chất lượng cao và chế độ bảo hành lâu dài.
Đặc Điểm Nổi Bật Của Quần Áo Bóng Rổ Nam
- Chất Liệu Cao Cấp: Quần áo bóng rổ nam thường được làm từ các loại vải thun lạnh, mè Thái hoặc mè Hàn Quốc, giúp tăng cường khả năng co giãn và thoáng mát khi vận động.
- Thiết Kế Đa Dạng: Các sản phẩm có thiết kế hiện đại, nhiều màu sắc và kiểu dáng phù hợp với sở thích cá nhân, từ phong cách đơn giản đến các mẫu thiết kế cầu kỳ, độc đáo.
- Phù Hợp Với Nhiều Đối Tượng: Không chỉ dành cho các vận động viên chuyên nghiệp, quần áo bóng rổ nam còn phù hợp cho người tập luyện thể thao thông thường hoặc sử dụng trong các hoạt động thường ngày.
Lợi Ích Khi Sử Dụng Quần Áo Bóng Rổ Nam
- Cải Thiện Hiệu Suất Vận Động: Với thiết kế chuyên biệt, quần áo bóng rổ nam giúp người mặc dễ dàng di chuyển, cải thiện hiệu suất khi thi đấu hoặc tập luyện.
- Thời Trang Và Phong Cách: Ngoài chức năng thể thao, quần áo bóng rổ còn là lựa chọn thời trang với nhiều phong cách cá tính, dễ dàng phối hợp với các trang phục khác.
- Bảo Vệ Cơ Thể: Chất liệu vải thoáng mát, thấm hút mồ hôi tốt giúp bảo vệ cơ thể khỏi các tác nhân gây hại từ môi trường, đồng thời giảm nguy cơ chấn thương khi vận động mạnh.
Các Xu Hướng Hiện Nay
- Thiết Kế Theo Yêu Cầu: Nhu cầu đặt may quần áo bóng rổ theo thiết kế riêng đang tăng cao, giúp các đội bóng có thể thể hiện bản sắc riêng qua trang phục thi đấu.
- Phong Cách Streetwear: Quần áo bóng rổ không chỉ giới hạn trong sân bóng mà còn được sử dụng như trang phục streetwear, tạo nên phong cách thời trang đường phố độc đáo.
Một Số Lưu Ý Khi Mua Quần Áo Bóng Rổ Nam
- Chọn Đúng Kích Cỡ: Đảm bảo chọn đúng kích cỡ để có trải nghiệm tốt nhất khi mặc, tránh tình trạng quá chật hoặc quá rộng làm ảnh hưởng đến hiệu suất vận động.
- Kiểm Tra Chất Liệu: Ưu tiên các loại vải có khả năng co giãn, thoáng khí và thấm hút mồ hôi tốt để đảm bảo sự thoải mái khi vận động.
- Xem Xét Thương Hiệu: Nên mua sản phẩm từ các thương hiệu uy tín để đảm bảo chất lượng và có chế độ bảo hành tốt.
Kết Luận
Quần áo bóng rổ nam tại Việt Nam ngày càng phát triển với nhiều sự lựa chọn về kiểu dáng, chất liệu và thương hiệu. Dù là để thi đấu, tập luyện hay chỉ đơn giản là để thể hiện phong cách cá nhân, quần áo bóng rổ nam luôn là lựa chọn lý tưởng cho những ai yêu thích thể thao và thời trang.

.png)
Mục Lục Tổng Hợp Về Quần Áo Bóng Rổ Nam
Quần áo bóng rổ nam không chỉ là trang phục thể thao mà còn là biểu tượng của phong cách sống năng động, cá tính. Dưới đây là mục lục chi tiết giúp bạn khám phá và lựa chọn quần áo bóng rổ nam phù hợp nhất:
- Giới Thiệu Chung Về Quần Áo Bóng Rổ Nam
Một cái nhìn tổng quan về quần áo bóng rổ nam, từ lịch sử hình thành đến vai trò quan trọng trong đời sống thể thao và thời trang.
- Các Thương Hiệu Quần Áo Bóng Rổ Nam Uy Tín Tại Việt Nam
Danh sách các thương hiệu nổi bật như Nike, Adidas, Under Armour, cùng với những ưu điểm nổi bật của từng thương hiệu.
- Hướng Dẫn Chọn Quần Áo Bóng Rổ Nam Phù Hợp
Các yếu tố cần lưu ý khi chọn quần áo bóng rổ, bao gồm chất liệu, kích thước, và thiết kế phù hợp với từng nhu cầu sử dụng.
- Xu Hướng Thời Trang Bóng Rổ Nam Mới Nhất
Cập nhật các xu hướng thời trang bóng rổ nam hiện nay, từ các mẫu thiết kế mới đến cách phối đồ để tạo nên phong cách riêng.
- Quần Áo Bóng Rổ Nam Chuyên Nghiệp: Chất Liệu Và Thiết Kế
Phân tích về các chất liệu phổ biến như vải thun lạnh, vải mè, và các kiểu thiết kế giúp tối ưu hóa hiệu suất thi đấu.
- Quần Áo Bóng Rổ Nam Thiết Kế Riêng: Đặt Hàng Theo Yêu Cầu
Giới thiệu về dịch vụ thiết kế quần áo bóng rổ theo yêu cầu, phù hợp với các đội bóng hoặc cá nhân muốn tạo sự khác biệt.
- Mua Sắm Quần Áo Bóng Rổ Nam Online: Các Trang Web Uy Tín
Hướng dẫn mua sắm trực tuyến, cùng với các trang web uy tín tại Việt Nam để đảm bảo chất lượng sản phẩm và dịch vụ hậu mãi tốt nhất.
- Cách Bảo Quản Và Giặt Giũ Quần Áo Bóng Rổ Nam
Những bí quyết bảo quản và giặt giũ để giữ cho quần áo bóng rổ luôn bền đẹp và giữ nguyên được chất lượng ban đầu.
- So Sánh Giá Cả Và Chất Lượng Quần Áo Bóng Rổ Nam Trên Thị Trường
Phân tích sự chênh lệch về giá cả và chất lượng giữa các thương hiệu quần áo bóng rổ nam trên thị trường Việt Nam.
- Đánh Giá Khách Hàng Về Các Sản Phẩm Quần Áo Bóng Rổ Nam
Ý kiến đánh giá từ người tiêu dùng về các sản phẩm quần áo bóng rổ nam, giúp bạn có cái nhìn tổng quan trước khi quyết định mua hàng.
10 Dạng Bài Tập Toán Có Lời Giải Hoàn Chỉnh
-
Bài Tập 1: Phân Tích Đa Thức Thành Nhân Tử
Cho đa thức \(P(x) = x^3 - 3x^2 + 4x - 12\). Hãy phân tích đa thức này thành nhân tử.
Lời giải: Sử dụng phương pháp nhóm hạng tử, ta có:
\[ P(x) = x^2(x - 3) + 4(x - 3) = (x - 3)(x^2 + 4) \] -
Bài Tập 2: Giải Phương Trình Bậc Hai
Giải phương trình bậc hai \(x^2 - 5x + 6 = 0\).
Lời giải: Sử dụng công thức nghiệm:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]Với \(a = 1\), \(b = -5\), \(c = 6\), ta có:
\[ x = \frac{5 \pm 1}{2} \Rightarrow x = 3 \, \text{hoặc} \, x = 2 \] -
Bài Tập 3: Tính Giá Trị Biểu Thức Đại Số
Tính giá trị biểu thức \(A = \frac{2x^2 - 3x + 1}{x - 1}\) tại \(x = 2\).
Lời giải: Thay \(x = 2\) vào biểu thức:
\[ A = \frac{2(2)^2 - 3(2) + 1}{2 - 1} = \frac{8 - 6 + 1}{1} = 3 \] -
Bài Tập 4: Định Lý Pythagore
Cho tam giác vuông có cạnh góc vuông lần lượt là 3 cm và 4 cm. Tính độ dài cạnh huyền.
Lời giải: Sử dụng định lý Pythagore:
\[ c^2 = a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25 \Rightarrow c = 5 \, \text{cm} \] -
Bài Tập 5: Ứng Dụng Đạo Hàm Trong Tính Toán Cực Trị
Tìm giá trị lớn nhất của hàm số \(f(x) = -x^2 + 4x + 1\) trên đoạn \([0, 3]\).
Lời giải: Tính đạo hàm \(f'(x)\) và tìm nghiệm của \(f'(x) = 0\):
\[ f'(x) = -2x + 4 \Rightarrow f'(x) = 0 \Rightarrow x = 2 \]Tính \(f(x)\) tại các điểm \(x = 0, 2, 3\) và so sánh:
\[ f(0) = 1, \, f(2) = 5, \, f(3) = 4 \Rightarrow \text{Giá trị lớn nhất là } 5 \, \text{tại } x = 2 \] -
Bài Tập 6: Tính Tích Phân Xác Định
Tính tích phân \(I = \int_{0}^{1} (3x^2 - 2x + 1) dx\).
Lời giải: Sử dụng công thức tích phân cơ bản:
\[ I = \left[ x^3 - x^2 + x \right]_{0}^{1} = (1 - 1 + 1) - (0 - 0 + 0) = 1 \] -
Bài Tập 7: Giải Hệ Phương Trình Tuyến Tính
Giải hệ phương trình:
\[ \begin{cases} 2x + y = 7 \\ x - y = 1 \end{cases} \]Lời giải: Phương pháp thế:
\[ y = x - 1 \Rightarrow 2x + (x - 1) = 7 \Rightarrow 3x = 8 \Rightarrow x = \frac{8}{3}, \, y = \frac{5}{3} \] -
Bài Tập 8: Tính Diện Tích Và Chu Vi Hình Học Phẳng
Tính diện tích và chu vi của hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.
Lời giải: Diện tích \(S = 5 \times 3 = 15 \, \text{cm}^2\), chu vi \(P = 2(5 + 3) = 16 \, \text{cm}\).
-
Bài Tập 9: Giải Bất Phương Trình
Giải bất phương trình \(2x - 3 > 1\).
Lời giải: Thực hiện các bước giải:
\[ 2x > 4 \Rightarrow x > 2 \] -
Bài Tập 10: Tìm Giá Trị Lớn Nhất Và Nhỏ Nhất Của Hàm Số
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(g(x) = x^2 - 4x + 3\) trên đoạn \([-1, 3]\).
Lời giải: Tính đạo hàm \(g'(x)\) và tìm nghiệm:
\[ g'(x) = 2x - 4 = 0 \Rightarrow x = 2 \]Tính \(g(x)\) tại các điểm \(x = -1, 2, 3\) và so sánh:
\[ g(-1) = 8, \, g(2) = -1, \, g(3) = 2 \Rightarrow \text{Giá trị lớn nhất là } 8, \text{nhỏ nhất là } -1 \]

Bài Tập 1: Phân Tích Đa Thức Thành Nhân Tử
Cho đa thức sau:
Hãy phân tích đa thức \(P(x)\) thành nhân tử.
Step 1: Nhóm các hạng tử
Trước tiên, chúng ta nhóm các hạng tử để dễ dàng nhận ra các nhân tử chung:
Ta nhận thấy các nhân tử chung ở mỗi nhóm là \(x^2\) và \(4\), nên ta có thể viết lại như sau:
Step 2: Đặt nhân tử chung
Ta thấy \(x - 3\) là nhân tử chung của cả hai nhóm, nên có thể đặt nhân tử này ra ngoài:
Kết luận:
Đa thức đã được phân tích thành nhân tử là:
Bài Tập 2: Giải Phương Trình Bậc Hai
Giải phương trình bậc hai sau:
Step 1: Xác định các hệ số
Ta có phương trình bậc hai tổng quát dạng \(ax^2 + bx + c = 0\), với:
- \(a = 1\)
- \(b = -5\)
- \(c = 6\)
Step 2: Tính delta (\(\Delta\))
Delta (\(\Delta\)) được tính theo công thức:
Thay các giá trị vào, ta có:
Step 3: Tính nghiệm của phương trình
Vì \(\Delta > 0\), phương trình có hai nghiệm phân biệt, được tính theo công thức:
Thay các giá trị vào, ta có:
Kết luận:
Phương trình có hai nghiệm là \(x_1 = 3\) và \(x_2 = 2\).

Bài Tập 3: Tính Giá Trị Biểu Thức Đại Số
Cho biểu thức đại số sau:
Tính giá trị của biểu thức \(A\) tại \(x = 2\).
Step 1: Thay giá trị \(x = 2\) vào biểu thức
Thay giá trị \(x = 2\) vào biểu thức \(A\), ta có:
Tiếp tục tính toán các giá trị trong biểu thức:
Step 2: Tính toán giá trị của biểu thức
Tiếp tục tính:
Kết luận:
Giá trị của biểu thức \(A\) tại \(x = 2\) là \(3\).
XEM THÊM:
Bài Tập 4: Định Lý Py-ta-go
Định lý Py-ta-go là một trong những định lý cơ bản và quan trọng nhất trong hình học, đặc biệt trong tam giác vuông. Định lý này được phát biểu như sau:
Trong một tam giác vuông, bình phương của cạnh huyền (cạnh dài nhất) bằng tổng bình phương của hai cạnh góc vuông.
Giả sử chúng ta có tam giác vuông với các cạnh tương ứng là \( a \), \( b \) và cạnh huyền là \( c \). Định lý Py-ta-go có thể được viết dưới dạng công thức:
\[ c^2 = a^2 + b^2 \]
Ví dụ 1: Áp Dụng Định Lý Py-ta-go
Xét một tam giác vuông có hai cạnh góc vuông lần lượt là 3 cm và 4 cm. Hãy tính độ dài cạnh huyền.
- Áp dụng công thức: \[ c^2 = a^2 + b^2 \]
- Thay các giá trị đã biết: \[ c^2 = 3^2 + 4^2 = 9 + 16 = 25 \]
- Tính cạnh huyền: \[ c = \sqrt{25} = 5 \text{ cm} \]
Vậy độ dài cạnh huyền là 5 cm.
Ví dụ 2: Kiểm Tra Một Tam Giác Có Phải Tam Giác Vuông Không
Cho tam giác với các cạnh lần lượt là 5 cm, 12 cm và 13 cm. Hãy kiểm tra xem tam giác này có phải là tam giác vuông hay không.
- Tính bình phương các cạnh: \[ 5^2 = 25 \], \[ 12^2 = 144 \], \[ 13^2 = 169 \]
- Kiểm tra xem \[ 13^2 = 5^2 + 12^2 \] có đúng không: \[ 169 = 25 + 144 \]
- Vì điều kiện trên đúng, nên tam giác với các cạnh 5 cm, 12 cm và 13 cm là tam giác vuông.
Ứng Dụng Thực Tế
Định lý Py-ta-go không chỉ là lý thuyết mà còn có nhiều ứng dụng thực tế, chẳng hạn như:
- Xác định khoảng cách trực tiếp giữa hai điểm trong không gian khi biết tọa độ của chúng.
- Giải quyết các vấn đề liên quan đến xây dựng, như tính toán kích thước của các yếu tố trong một cấu trúc hình học phẳng.
Với định lý Py-ta-go, chúng ta có thể dễ dàng tính toán và giải quyết nhiều bài toán liên quan đến tam giác vuông và các ứng dụng trong cuộc sống hằng ngày.
Bài Tập 5: Ứng Dụng Đạo Hàm Trong Tính Toán Cực Trị
Trong toán học, đạo hàm được sử dụng rộng rãi để tìm cực trị của hàm số, tức là giá trị lớn nhất và nhỏ nhất mà hàm số có thể đạt được trong một khoảng nhất định. Để thực hiện điều này, chúng ta thực hiện các bước sau:
- Tìm đạo hàm của hàm số:
Giả sử hàm số cần tìm cực trị là \(f(x)\). Trước tiên, chúng ta tính đạo hàm của hàm số này, ký hiệu là \(f'(x)\).
- Giải phương trình \(f'(x) = 0\):
Để tìm các điểm khả nghi có thể là cực trị, chúng ta giải phương trình \(f'(x) = 0\). Các nghiệm của phương trình này là các giá trị \(x\) tại đó hàm số có thể đạt cực trị.
- Xét dấu của đạo hàm:
Sau khi tìm được các nghiệm \(x_1, x_2, \dots\), ta cần xét dấu của \(f'(x)\) trong các khoảng mà các nghiệm này chia trục số. Điều này giúp xác định các đoạn tăng, giảm của hàm số:
- Nếu \(f'(x)\) đổi dấu từ dương sang âm tại \(x_i\), thì \(f(x_i)\) là giá trị cực đại.
- Nếu \(f'(x)\) đổi dấu từ âm sang dương tại \(x_i\), thì \(f(x_i)\) là giá trị cực tiểu.
- Tính giá trị cực trị:
Cuối cùng, thay các giá trị \(x_i\) tìm được vào hàm số gốc \(f(x)\) để tính giá trị của cực trị.
Ví dụ: Tìm cực trị của hàm số \(f(x) = 3x^4 - 4x^3 + 6x^2 - 2\).
- Bước 1: Tính đạo hàm \(f'(x) = 12x^3 - 12x^2 + 12x\).
- Bước 2: Giải phương trình \(12x^3 - 12x^2 + 12x = 0\), ta được các nghiệm \(x = 0\) và \(x = 1\).
- Bước 3: Xét dấu của đạo hàm trên các khoảng:
- Trên khoảng \( (-\infty, 0) \): \(f'(x) > 0\)
- Trên khoảng \( (0, 1) \): \(f'(x) < 0\)
- Trên khoảng \( (1, \infty) \): \(f'(x) > 0\)
- Bước 4: Do đó, \(f(0)\) là giá trị cực đại và \(f(1)\) là giá trị cực tiểu của hàm số.
Như vậy, việc sử dụng đạo hàm để tìm cực trị không chỉ giúp ta hiểu rõ hơn về hành vi của hàm số mà còn rất hữu ích trong các bài toán thực tế, như tối ưu hóa chi phí hoặc lợi nhuận trong kinh doanh.

Bài Tập 6: Tính Tích Phân Xác Định
Tích phân xác định là một trong những khái niệm quan trọng trong giải tích, giúp tính diện tích dưới đường cong của một hàm số trong một khoảng nhất định. Để tính tích phân xác định, chúng ta thường sử dụng các bước sau:
- Xác định hàm số cần tích phân:
Giả sử hàm số cần tích phân là \( f(x) \). Bạn cần xác định hàm số này dựa trên bài toán cụ thể.
- Chọn giới hạn tích phân:
Giới hạn tích phân là hai giá trị \( a \) và \( b \) mà tại đó bạn muốn tính diện tích dưới đường cong. Ví dụ, nếu bạn muốn tính diện tích từ \( x = 1 \) đến \( x = 3 \), thì giới hạn tích phân sẽ là \( a = 1 \) và \( b = 3 \).
- Viết công thức tích phân:
Công thức tổng quát của tích phân xác định là:
\[ \int_{a}^{b} f(x) \, dx \]Trong đó, \( f(x) \) là hàm số cần tích phân, \( a \) và \( b \) là giới hạn tích phân.
- Tính tích phân:
Sử dụng các phương pháp như công thức nguyên hàm hoặc các quy tắc tích phân (tích phân từng phần, thay đổi biến,...) để tính giá trị của tích phân xác định.
- Diễn giải kết quả:
Kết quả của tích phân xác định thường là diện tích dưới đường cong của hàm số từ \( x = a \) đến \( x = b \). Kết quả này có thể mang ý nghĩa hình học, vật lý hoặc ứng dụng khác tùy vào bài toán.
Ví dụ, tính tích phân xác định của hàm số \( f(x) = x^2 \) từ \( x = 1 \) đến \( x = 3 \):
Kết quả tích phân là \( \frac{26}{3} \), tương ứng với diện tích dưới đường cong của hàm số \( x^2 \) từ \( x = 1 \) đến \( x = 3 \).
Bài Tập 7: Giải Hệ Phương Trình Tuyến Tính
Trong toán học, hệ phương trình tuyến tính là một tập hợp các phương trình bậc nhất, và chúng ta cần tìm giá trị của các biến thỏa mãn tất cả các phương trình này. Bài tập này sẽ hướng dẫn bạn cách giải hệ phương trình tuyến tính một cách chi tiết.
Bước 1: Viết hệ phương trình dưới dạng ma trận
Giả sử chúng ta có hệ phương trình:
- \(2x + 3y = 6\)
- \(4x - y = 5\)
Hệ phương trình này có thể được biểu diễn dưới dạng ma trận như sau:
Bước 2: Sử dụng phương pháp thế hoặc phương pháp cộng đại số
Phương pháp thế: Ta giải một trong hai phương trình để tìm một biến, rồi thế vào phương trình còn lại.
- Từ phương trình đầu tiên, ta có: \(y = \frac{6 - 2x}{3}\)
- Thế giá trị của \(y\) vào phương trình thứ hai:
- \(4x - \frac{6 - 2x}{3} = 5\)
- Giải phương trình này để tìm giá trị của \(x\), sau đó thế ngược lại để tìm \(y\).
Phương pháp cộng đại số: Ta cộng hoặc trừ các phương trình để loại bỏ một trong các biến, sau đó giải phương trình còn lại.
- Cộng cả hai phương trình để loại bỏ \(y\):
- \(2(2x + 3y) + (4x - y) = 2(6) + 5\)
- Từ đó ta giải ra giá trị của \(x\) và sau đó là \(y\).
Bước 3: Kiểm tra kết quả
Thay các giá trị \(x\) và \(y\) tìm được vào cả hai phương trình ban đầu để đảm bảo chúng đúng.
Giải hệ phương trình tuyến tính không chỉ là một công cụ quan trọng trong toán học mà còn ứng dụng rộng rãi trong nhiều lĩnh vực như kinh tế, vật lý, và kỹ thuật. Hiểu rõ các phương pháp giải sẽ giúp bạn nắm vững kiến thức này và áp dụng hiệu quả trong các bài toán thực tế.
Bài Tập 8: Tính Diện Tích Và Chu Vi Hình Học Phẳng
Trong bài tập này, chúng ta sẽ cùng ôn lại và thực hành tính diện tích và chu vi của các hình học phẳng quen thuộc như hình tròn, hình tam giác, hình vuông, và hình chữ nhật.
1. Công Thức Tính Diện Tích Và Chu Vi
- Hình Vuông:
- Diện tích: \[S = a^2\], trong đó \(a\) là độ dài một cạnh của hình vuông.
- Chu vi: \[P = 4a\].
- Hình Chữ Nhật:
- Diện tích: \[S = l \times w\], trong đó \(l\) là chiều dài và \(w\) là chiều rộng.
- Chu vi: \[P = 2(l + w)\].
- Hình Tam Giác:
- Diện tích: \[S = \frac{1}{2} \times b \times h\], trong đó \(b\) là độ dài cạnh đáy và \(h\) là chiều cao.
- Chu vi: \[P = a + b + c\], trong đó \(a\), \(b\), \(c\) là độ dài các cạnh của tam giác.
- Hình Tròn:
- Diện tích: \[S = \pi r^2\], trong đó \(r\) là bán kính của hình tròn.
- Chu vi: \[C = 2\pi r\].
2. Ví Dụ Thực Hành
Hãy giải bài toán sau:
Cho hình chữ nhật có chiều dài là 10cm và chiều rộng là 5cm. Hãy tính diện tích và chu vi của hình chữ nhật này.
- Giải:
- Diện tích của hình chữ nhật là: \[S = 10 \times 5 = 50\ cm^2\].
- Chu vi của hình chữ nhật là: \[P = 2(10 + 5) = 30\ cm\].
3. Bài Tập Tự Giải
Hãy áp dụng các công thức trên để giải các bài tập sau:
- Tính diện tích và chu vi của một hình tròn có bán kính 7cm.
- Tính diện tích và chu vi của một hình tam giác có các cạnh dài 3cm, 4cm, và 5cm.
- Tính diện tích và chu vi của một hình vuông có cạnh dài 6cm.
Hãy đảm bảo rằng bạn hiểu và có thể áp dụng các công thức này vào các bài toán thực tế.
Bài Tập 9: Giải Bất Phương Trình
Trong toán học, bất phương trình là một phần quan trọng, thường xuất hiện trong các bài toán thực tế cũng như lý thuyết. Để giải một bất phương trình, ta cần hiểu rõ các quy tắc và phương pháp giải cơ bản.
Mục tiêu: Trong bài tập này, chúng ta sẽ cùng tìm hiểu cách giải bất phương trình thông qua các bước chi tiết sau:
- Xác định điều kiện của bất phương trình: Trước khi giải, cần xác định miền xác định của biến số trong bất phương trình. Ví dụ, với bất phương trình chứa phân số, mẫu số phải khác 0.
- Chuyển đổi bất phương trình về dạng cơ bản: Sử dụng các phép biến đổi tương đương như cộng, trừ, nhân, chia hai vế của bất phương trình với một số để đưa về dạng đơn giản nhất. Lưu ý khi nhân hoặc chia hai vế của bất phương trình với một số âm, dấu bất phương trình phải đổi chiều.
- Giải bất phương trình: Sau khi đã đơn giản hóa, ta giải bất phương trình như một phương trình bình thường để tìm ra nghiệm.
- Biểu diễn nghiệm trên trục số: Sau khi tìm được nghiệm của bất phương trình, ta biểu diễn nó trên trục số để dễ dàng nhận biết khoảng giá trị của nghiệm.
- Kết luận: Từ nghiệm đã tìm, xác định khoảng giá trị thỏa mãn bất phương trình và kết luận đáp án.
Ví dụ:
Giải bất phương trình sau:
Giải:
- Chuyển \( x \) từ phải sang trái và \( 3 \) từ trái sang phải: \[ 2x + x > 5 + 3 \]
- Sau đó, ta có: \[ 3x > 8 \]
- Chia cả hai vế cho 3: \[ x > \frac{8}{3} \]
Vậy nghiệm của bất phương trình là \( x > \frac{8}{3} \). Trên trục số, ta biểu diễn bằng đoạn thẳng mở từ \( \frac{8}{3} \) về phía dương.
Qua bài tập này, các bạn đã học được cách giải và biểu diễn nghiệm của một bất phương trình đơn giản, là bước cơ bản để giải các bài toán phức tạp hơn sau này.
Bài Tập 10: Tìm Giá Trị Lớn Nhất Và Nhỏ Nhất Của Hàm Số
Trong bài tập này, chúng ta sẽ tìm hiểu cách xác định giá trị lớn nhất và nhỏ nhất của một hàm số, một khái niệm quan trọng trong toán học và ứng dụng trong nhiều lĩnh vực như kinh tế, kỹ thuật, và vật lý.
Bước 1: Xác định hàm số cần tìm cực trị
Giả sử chúng ta có một hàm số \(f(x)\). Nhiệm vụ của chúng ta là tìm các giá trị lớn nhất (maxima) và nhỏ nhất (minima) của hàm số này trên một đoạn xác định.
Bước 2: Tìm đạo hàm của hàm số
Để tìm các điểm cực trị, chúng ta cần tính đạo hàm bậc nhất của hàm số \(f(x)\), ký hiệu là \(f'(x)\). Các điểm tại đó \(f'(x) = 0\) hoặc \(f'(x)\) không xác định có thể là các điểm cực trị.
Bước 3: Giải phương trình \(f'(x) = 0\)
Giải phương trình \(f'(x) = 0\) để tìm các giá trị của \(x\) ứng với các điểm cực trị khả dĩ.
Bước 4: Xét dấu đạo hàm hoặc sử dụng đạo hàm bậc hai
Sau khi tìm được các giá trị \(x\) từ bước 3, chúng ta cần kiểm tra dấu của đạo hàm hoặc tính đạo hàm bậc hai \(f''(x)\) để xác định đó là điểm cực đại hay cực tiểu:
- Nếu \(f''(x) > 0\) tại điểm đó, thì đó là một cực tiểu.
- Nếu \(f''(x) < 0\) tại điểm đó, thì đó là một cực đại.
Bước 5: Tìm giá trị lớn nhất và nhỏ nhất trên đoạn [a, b]
Sau khi đã xác định được các điểm cực trị, chúng ta cần so sánh giá trị của hàm số tại các điểm cực trị này và tại các điểm biên \(x = a\) và \(x = b\) của đoạn để xác định giá trị lớn nhất và nhỏ nhất.
Ví dụ:
Xét hàm số \(f(x) = x^3 - 3x + 2\) trên đoạn \([-2, 2]\).
- Tính đạo hàm: \(f'(x) = 3x^2 - 3\).
- Giải phương trình \(f'(x) = 0\): \(3x^2 - 3 = 0\), suy ra \(x = \pm 1\).
- Tính giá trị hàm số tại các điểm biên và các điểm cực trị:
- \(f(-2) = -8 + 6 + 2 = 0\).
- \(f(-1) = -1 + 3 + 2 = 4\).
- \(f(1) = 1 - 3 + 2 = 0\).
- \(f(2) = 8 - 6 + 2 = 4\).
- So sánh các giá trị trên để kết luận: Giá trị lớn nhất của hàm số trên đoạn này là 4, giá trị nhỏ nhất là 0.
Như vậy, bằng cách áp dụng phương pháp trên, chúng ta có thể dễ dàng tìm được giá trị lớn nhất và nhỏ nhất của bất kỳ hàm số nào trên một đoạn xác định.