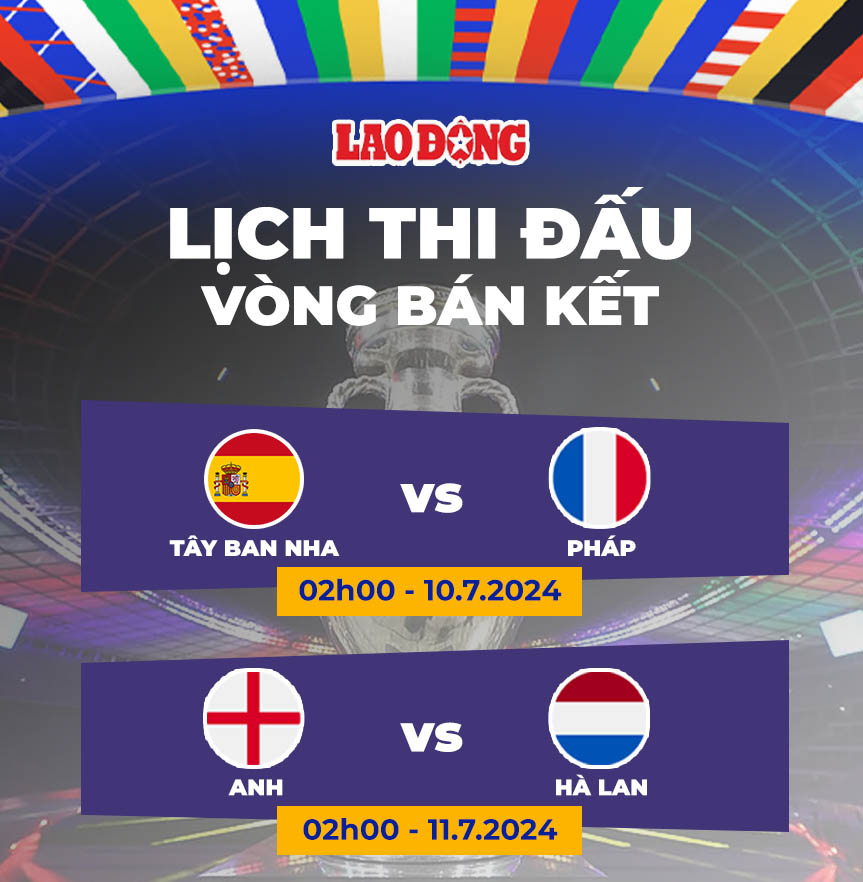
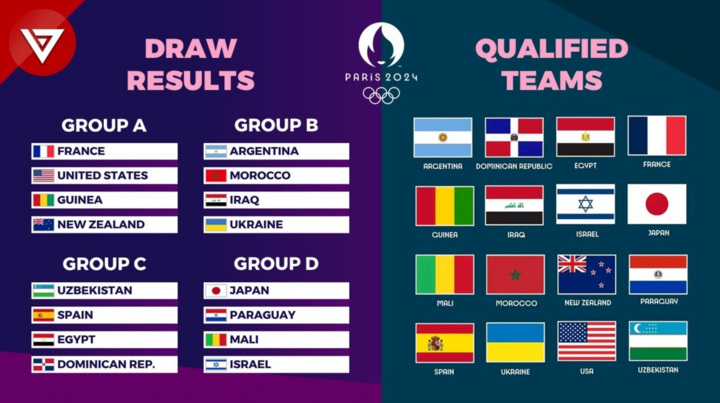
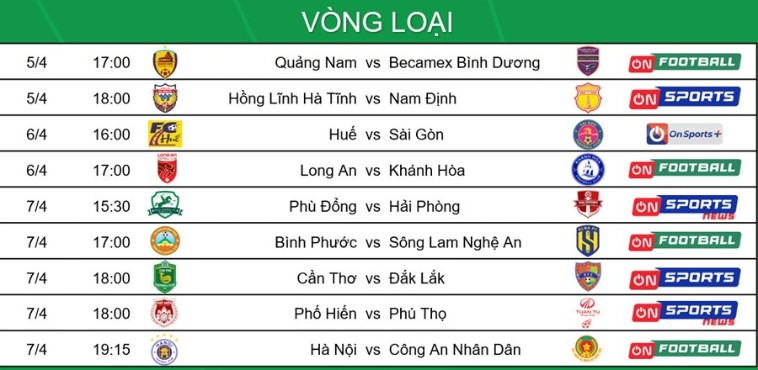
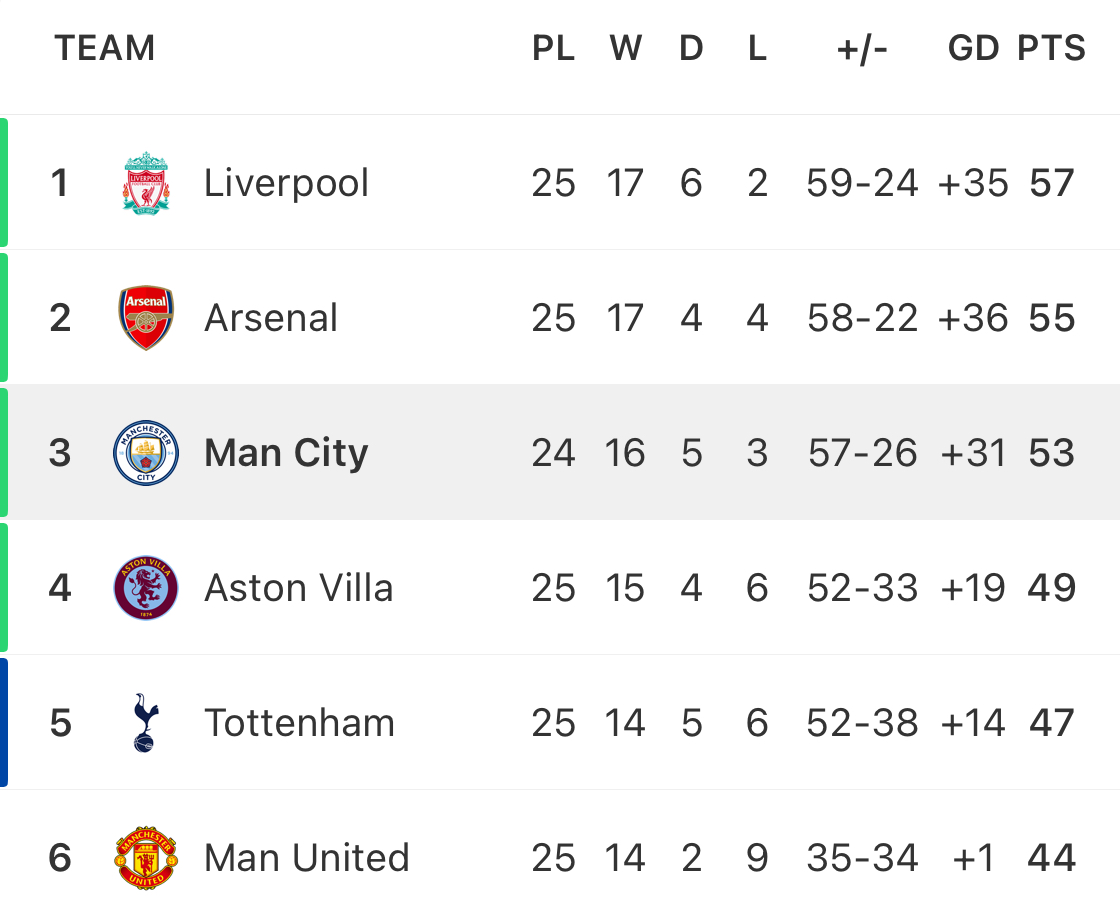
Chủ đề game bóng đá mobile hay nhất: Khám phá danh sách game bóng đá mobile hay nhất hiện nay, nơi bạn có thể tìm thấy những tựa game đỉnh cao với đồ họa ấn tượng, lối chơi cuốn hút và trải nghiệm bóng đá sống động ngay trên thiết bị di động của mình. Cùng tìm hiểu ngay để không bỏ lỡ bất kỳ siêu phẩm nào!
Mục lục
- Top Game Bóng Đá Mobile Hay Nhất
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Toán Có Lời Giải
- Bài Tập 1: Giải Phương Trình Bậc 2
- Bài Tập 2: Hệ Phương Trình Tuyến Tính
- Bài Tập 3: Tính Đạo Hàm Hàm Số
- Bài Tập 4: Tích Phân Bất Định
- Bài Tập 5: Giải Bất Phương Trình
- Bài Tập 6: Phương Trình Logarit
- Bài Tập 7: Dãy Số Và Cấp Số
- Bài Tập 8: Hình Học Không Gian
- Bài Tập 9: Tính Giá Trị Lượng Giác
- Bài Tập 10: Giải Bài Toán Thực Tế
Top Game Bóng Đá Mobile Hay Nhất
Bóng đá là môn thể thao vua và là nguồn cảm hứng cho rất nhiều trò chơi di động. Dưới đây là danh sách các tựa game bóng đá mobile hay nhất, được đánh giá cao bởi cộng đồng game thủ.
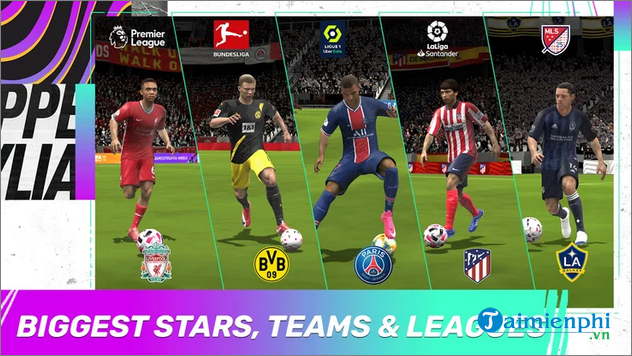
1. FIFA Mobile
FIFA Mobile là tựa game bóng đá chính thức từ EA Sports, với hơn 600 đội bóng và hơn 15.000 cầu thủ được cấp phép. Trò chơi mang đến trải nghiệm bóng đá chân thực trên thiết bị di động, với các chế độ chơi đa dạng như FIFA Ultimate Team và PvE, PvP. Mùa giải 2023 đã cập nhật đầy đủ các đội bóng, cầu thủ, và giải đấu.
2. eFootball 2023
Được phát triển bởi Konami, eFootball 2023 là phiên bản nâng cấp của dòng game Pro Evolution Soccer (PES). Trò chơi nổi bật với đồ họa sắc nét, hệ thống điều khiển mượt mà và chế độ chơi eFootball World cho phép game thủ thi đấu với những người chơi khác trên toàn thế giới.
3. Dream League Soccer 2023
Dream League Soccer 2023 là một tựa game quản lý bóng đá, nơi bạn có thể tạo đội bóng của riêng mình từ hơn 4000 cầu thủ được cấp phép. Trò chơi cung cấp nhiều tính năng như xây dựng sân vận động, tùy chỉnh trang phục, và tham gia các giải đấu quốc tế.
4. Soccer Manager 2024
Soccer Manager 2024 là tựa game mô phỏng quản lý đội bóng, cho phép bạn điều hành đội bóng từ việc ký hợp đồng với cầu thủ, quản lý tài chính, đến sắp xếp chiến thuật. Trò chơi có hơn 25.000 cầu thủ và 900 câu lạc bộ từ 35 quốc gia.
5. Top Eleven VNG
Top Eleven VNG là phiên bản Việt Nam của tựa game quản lý bóng đá nổi tiếng Top Eleven. Trò chơi mang đến trải nghiệm chân thực khi bạn trở thành huấn luyện viên, ký hợp đồng với các siêu sao, và xây dựng câu lạc bộ của mình.
6. Soccer Star 24 Super Football
Soccer Star 24 Super Football là trò chơi kết hợp giữa thi đấu bóng đá và mô phỏng cuộc sống của một siêu sao bóng đá. Bạn có thể tranh tài ở các giải đấu lớn, đồng thời tận hưởng cuộc sống xa hoa với nhà cửa, xe hơi và các trang phục phong cách.
7. Head Ball 2
Head Ball 2 là một trò chơi bóng đá độc đáo với lối chơi vui nhộn, nơi bạn điều khiển các cầu thủ với chiếc đầu to và thi đấu trong các trận đấu 1v1 trực tuyến. Game có đồ họa dễ thương và cơ chế điều khiển đơn giản, mang đến những trận đấu sôi động và đầy bất ngờ.
Tổng Kết
Những tựa game bóng đá mobile này đều mang đến trải nghiệm tuyệt vời cho người chơi. Từ việc quản lý đội bóng đến thi đấu trực tuyến, mỗi trò chơi đều có những điểm nhấn riêng, phù hợp với sở thích của từng game thủ.
.png)
Mục Lục Tổng Hợp
Top 10 game bóng đá mobile hay nhất 2024
Tổng hợp các tựa game bóng đá được yêu thích nhất trong năm 2024.
Những tựa game bóng đá thú vị và độc đáo
Khám phá những trò chơi bóng đá với phong cách mới lạ và thú vị.
Game bóng đá offline đáng chơi nhất
Danh sách các game bóng đá có thể chơi mà không cần kết nối Internet.
Trò chơi bóng đá trực tuyến hấp dẫn
Giới thiệu các game bóng đá có chế độ chơi online thú vị.
Hướng dẫn chơi game bóng đá hiệu quả
Một số mẹo và chiến lược để trở thành người chơi giỏi hơn.
Những tính năng nổi bật trong game bóng đá mobile
Những tính năng đáng chú ý giúp tăng trải nghiệm khi chơi game.
So sánh các game bóng đá mobile phổ biến
So sánh điểm mạnh và yếu của từng tựa game.
Những lưu ý khi chơi game bóng đá trên di động
Thông tin hữu ích giúp bạn tránh gặp rắc rối khi chơi game.
10 Dạng Bài Tập Toán Có Lời Giải
- Phương trình bậc 2
- Hệ phương trình tuyến tính
- Đạo hàm của hàm số
- Tích phân bất định
- Bất phương trình
- Phương trình logarit
- Dãy số và cấp số
- Hình học không gian
- Giải bài toán thực tế
- Tính giá trị lượng giác
Giải phương trình bậc 2 dạng \[ax^2 + bx + c = 0\]. Phân tích và tìm nghiệm bằng cách sử dụng công thức nghiệm và định lý Viet.
Giải hệ phương trình tuyến tính hai ẩn \[\begin{cases} ax + by = c \\ dx + ey = f \end{cases}\]. Sử dụng phương pháp thế và phương pháp cộng đại số để tìm nghiệm.
Tính đạo hàm của các hàm số dạng \[y = f(x)\], bao gồm hàm bậc nhất, bậc hai, và hàm đa thức.
Tính tích phân của các hàm số dạng \[\int f(x)dx\], bao gồm hàm số mũ, hàm lượng giác, và đa thức.
Giải các bất phương trình dạng \[ax + b \leq 0\], \[ax^2 + bx + c > 0\] và phân tích miền nghiệm trên trục số.
Giải phương trình logarit dạng \[\log_a(x) = b\], bao gồm việc biến đổi và tìm nghiệm dựa trên tính chất logarit.
Tìm số hạng tổng quát và tính tổng của dãy số, cấp số cộng, cấp số nhân. Ví dụ: \[a_n = a_1 + (n-1)d\] cho cấp số cộng.
Tính toán thể tích, diện tích của các hình khối trong không gian như hình lập phương, hình chóp, hình cầu.
Sử dụng các kiến thức toán học để giải các bài toán thực tế liên quan đến khoảng cách, thời gian, vận tốc.
Tính toán các giá trị lượng giác của các góc đặc biệt, bao gồm \[\sin\], \[\cos\], \[\tan\] và ứng dụng trong tam giác vuông.

Bài Tập 1: Giải Phương Trình Bậc 2
Trong bài tập này, chúng ta sẽ giải phương trình bậc 2 có dạng tổng quát:
Với \(a\), \(b\), và \(c\) là các hệ số thực và \(a \neq 0\). Để giải phương trình bậc 2, ta sẽ thực hiện các bước sau:
- Tính Delta (\(\Delta\)):
- Xét dấu của Delta:
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép.
- Nếu \(\Delta < 0\): Phương trình vô nghiệm trong tập số thực.
- Tính nghiệm của phương trình:
- Nếu \(\Delta > 0\), nghiệm được tính theo công thức: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a} \quad \text{và} \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
- Nếu \(\Delta = 0\), nghiệm kép duy nhất là: \[ x = \frac{-b}{2a} \]
Delta được tính theo công thức:
\[ \Delta = b^2 - 4ac \]Ví dụ: Giải phương trình sau:
Giải:
- Tính Delta: \[ \Delta = (-4)^2 - 4 \times 2 \times (-6) = 16 + 48 = 64 \]
- Vì \(\Delta > 0\), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{4 + \sqrt{64}}{4} = \frac{12}{4} = 3 \quad \text{và} \quad x_2 = \frac{4 - \sqrt{64}}{4} = \frac{-4}{4} = -1 \]
Vậy nghiệm của phương trình là \(x_1 = 3\) và \(x_2 = -1\).

Bài Tập 2: Hệ Phương Trình Tuyến Tính
Trong bài tập này, chúng ta sẽ giải hệ phương trình tuyến tính hai ẩn số có dạng:
Với \(a\), \(b\), \(c\), \(d\), \(e\), và \(f\) là các hệ số thực. Để giải hệ phương trình này, chúng ta có thể sử dụng hai phương pháp phổ biến là phương pháp thế và phương pháp cộng đại số.
- Phương pháp thế:
- Giải một trong hai phương trình để tìm \(x\) hoặc \(y\) theo ẩn còn lại.
- Thế giá trị của \(x\) hoặc \(y\) vào phương trình còn lại để tìm nghiệm.
- Phương pháp cộng đại số:
- Nhân hai phương trình với các hệ số thích hợp để khi cộng hoặc trừ hai phương trình, một ẩn sẽ được triệt tiêu.
- Giải phương trình một ẩn còn lại để tìm giá trị của ẩn đó.
- Thay giá trị tìm được vào một trong hai phương trình ban đầu để tìm nghiệm còn lại.
Ví dụ: Giải hệ phương trình sau:
Giải:
- Sử dụng phương pháp thế:
Từ phương trình thứ hai, giải \(y\) theo \(x\):
\[ y = 4x - 11 \]Thế \(y = 4x - 11\) vào phương trình thứ nhất:
\[ 2x + 3(4x - 11) = 5 \]Giải phương trình này để tìm \(x\):
\[ 2x + 12x - 33 = 5 \\ 14x = 38 \\ x = \frac{38}{14} = \frac{19}{7} \]Thay giá trị \(x\) vào phương trình thứ hai để tìm \(y\):
\[ y = 4\left(\frac{19}{7}\right) - 11 = \frac{76}{7} - 11 = \frac{76}{7} - \frac{77}{7} = -\frac{1}{7} \]Vậy nghiệm của hệ phương trình là \(x = \frac{19}{7}\) và \(y = -\frac{1}{7}\).

Bài Tập 3: Tính Đạo Hàm Hàm Số
Trong bài tập này, chúng ta sẽ tính đạo hàm của một số hàm số thường gặp. Đạo hàm là một khái niệm quan trọng trong giải tích, cho biết sự thay đổi của hàm số khi biến số thay đổi. Công thức tính đạo hàm cơ bản cho một hàm số dạng tổng quát như sau:
Dưới đây là các bước cụ thể để tính đạo hàm:
- Tính đạo hàm của hàm số bậc nhất:
- Tính đạo hàm của hàm số bậc hai:
- Tính đạo hàm của hàm đa thức:
- Ví dụ cụ thể:
Đạo hàm của hàm số dạng \(f(x) = ax + b\) được tính như sau:
\[ f'(x) = a \]Đạo hàm của hàm số dạng \(f(x) = ax^2 + bx + c\) là:
\[ f'(x) = 2ax + b \]Đối với một hàm đa thức tổng quát \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0\), đạo hàm của hàm số là:
\[ f'(x) = na_nx^{n-1} + (n-1)a_{n-1}x^{n-2} + \ldots + a_1 \]Cho hàm số \(f(x) = 3x^3 - 5x^2 + 2x - 7\). Tính đạo hàm của hàm số này.
Giải:
\[ f'(x) = 3 \times 3x^2 - 5 \times 2x + 2 = 9x^2 - 10x + 2 \]Vậy đạo hàm của hàm số \(f(x)\) là \(f'(x) = 9x^2 - 10x + 2\).
XEM THÊM:
Bài Tập 4: Tích Phân Bất Định
Trong giải tích, tích phân bất định của một hàm số là một dạng toán học quan trọng giúp xác định diện tích dưới đường cong của hàm số đó. Bài tập dưới đây sẽ hướng dẫn bạn cách tính tích phân bất định cơ bản với các ví dụ minh họa chi tiết.
Ví dụ 1: Tích phân bất định của hàm đa thức
Xét hàm số \( f(x) = 3x^2 + 5x - 2 \). Tích phân bất định của hàm số này được tính như sau:
- Bước 1: Áp dụng quy tắc tích phân cho mỗi hạng tử của hàm số.
- Bước 2: Tích phân của \( 3x^2 \) là \( \frac{3x^3}{3} = x^3 \).
- Bước 3: Tích phân của \( 5x \) là \( \frac{5x^2}{2} \).
- Bước 4: Tích phân của \( -2 \) là \( -2x \).
- Bước 5: Tổng hợp kết quả, ta có tích phân bất định của \( f(x) \) là: \[ \int (3x^2 + 5x - 2) \, dx = x^3 + \frac{5x^2}{2} - 2x + C \] trong đó, \( C \) là hằng số tích phân.
Ví dụ 2: Tích phân bất định của hàm lượng giác
Xét hàm số \( g(x) = \cos(x) \). Để tính tích phân bất định của hàm này, ta làm như sau:
- Bước 1: Xác định công thức tích phân của hàm \( \cos(x) \).
- Bước 2: Theo công thức, ta có: \[ \int \cos(x) \, dx = \sin(x) + C \]
Ví dụ 3: Tích phân bất định của hàm mũ
Xét hàm số \( h(x) = e^x \). Tích phân bất định của hàm này được tính như sau:
- Bước 1: Nhận diện dạng hàm mũ \( e^x \).
- Bước 2: Tích phân của hàm mũ \( e^x \) là chính nó: \[ \int e^x \, dx = e^x + C \]
Bài tập tự luyện
Hãy thử tính các tích phân bất định sau:
- \( \int (2x^3 - 4x + 1) \, dx \)
- \( \int \sin(x) \, dx \)
- \( \int e^{2x} \, dx \)
Ghi chú: Đừng quên cộng hằng số tích phân \( C \) vào kết quả cuối cùng của mỗi bài tập.

Bài Tập 5: Giải Bất Phương Trình
Bất phương trình là một phần quan trọng trong toán học, đặc biệt trong các bài toán liên quan đến bất đẳng thức và chứng minh. Để giải một bất phương trình, chúng ta cần thực hiện các bước sau đây:
- Xác định tập xác định: Trước khi giải bất phương trình, hãy xác định tập xác định của bất phương trình. Điều này bao gồm việc kiểm tra các giá trị mà biểu thức có nghĩa, chẳng hạn như phân thức không được có mẫu số bằng 0.
- Biến đổi bất phương trình về dạng chuẩn: Đưa bất phương trình về dạng cơ bản nhất. Ví dụ, đối với bất phương trình bậc nhất một ẩn, ta cố gắng đưa về dạng \( ax + b \geq 0 \).
- Xét dấu của từng biểu thức: Phân tích dấu của các biểu thức có trong bất phương trình. Nếu bất phương trình chứa nhiều biểu thức, hãy xác định khoảng mà mỗi biểu thức có giá trị dương hoặc âm.
- Vẽ bảng xét dấu: Sử dụng bảng xét dấu để xác định khoảng giá trị của ẩn số mà bất phương trình thỏa mãn. Điều này thường áp dụng với bất phương trình bậc hai hoặc bất phương trình chứa phân thức.
- Giải bất phương trình: Kết hợp các khoảng giá trị từ bảng xét dấu để tìm nghiệm của bất phương trình. Đây là bước quan trọng để xác định giải pháp tổng thể.
- Viết kết luận: Tổng hợp các khoảng nghiệm lại thành nghiệm tổng quát cho bất phương trình. Đảm bảo rằng các nghiệm này nằm trong tập xác định đã xác định ban đầu.
Ví dụ, giải bất phương trình \( \frac{2x + 3}{x - 1} \geq 0 \):
- Xác định tập xác định: \( x \neq 1 \)
- Biến đổi về dạng chuẩn: \( \frac{2x + 3}{x - 1} \geq 0 \)
- Xét dấu của \( 2x + 3 \) và \( x - 1 \):
- Lập bảng xét dấu:
- Kết luận nghiệm: \( x \in (-\infty, -\frac{3}{2}) \cup (1, \infty) \)
| Khoảng | Biểu thức \( 2x + 3 \) | Biểu thức \( x - 1 \) | Tích dấu |
|---|---|---|---|
| \( (-\infty, -\frac{3}{2}) \) | - | - | + |
| \( (-\frac{3}{2}, 1) \) | + | - | - |
| \( (1, \infty) \) | + | + | + |

Bài Tập 6: Phương Trình Logarit
Phương trình logarit là một dạng toán học quan trọng thường xuất hiện trong các bài tập giải tích. Việc giải phương trình logarit yêu cầu bạn phải hiểu rõ các tính chất của logarit cũng như cách biến đổi chúng một cách hợp lý.
Các bước giải phương trình logarit
- Đưa phương trình về dạng đơn giản nhất: Đầu tiên, hãy cố gắng đưa các logarit về cùng một cơ số nếu có thể. Nếu phương trình có dạng \( \log_a{f(x)} = \log_a{g(x)} \), thì ta có thể loại bỏ logarit để được phương trình \( f(x) = g(x) \).
- Sử dụng các tính chất của logarit: Các tính chất cơ bản của logarit như: \[ \log_a{(xy)} = \log_a{x} + \log_a{y} \] \[ \log_a{\left(\frac{x}{y}\right)} = \log_a{x} - \log_a{y} \] \[ \log_a{x^n} = n\log_a{x} \] rất hữu ích trong việc biến đổi phương trình về dạng dễ giải hơn.
- Giải phương trình mới: Sau khi loại bỏ logarit hoặc sử dụng các tính chất của logarit, bạn sẽ được một phương trình mới. Giải phương trình này như bình thường để tìm ra nghiệm.
- Kiểm tra nghiệm: Để đảm bảo rằng các nghiệm tìm được là hợp lệ, hãy kiểm tra lại trong phương trình ban đầu vì logarit chỉ xác định khi giá trị bên trong của nó dương.
Ví dụ 1: Giải phương trình \( \log_2{(x+1)} = \log_2{(3x-5)} \)
- Bước 1: Loại bỏ logarit bằng cách áp dụng tính chất của logarit, ta được: \[ x + 1 = 3x - 5 \]
- Bước 2: Giải phương trình bậc nhất: \[ 2x = 6 \Rightarrow x = 3 \]
- Bước 3: Kiểm tra nghiệm: \( x = 3 \) thỏa mãn điều kiện của phương trình ban đầu \( x+1 > 0 \) và \( 3x-5 > 0 \). Vậy \( x = 3 \) là nghiệm của phương trình.
Ví dụ 2: Giải phương trình \( \log_3{(x^2 - 2x)} = 2 \)
- Bước 1: Đưa phương trình về dạng mũ: \[ x^2 - 2x = 3^2 = 9 \]
- Bước 2: Giải phương trình bậc hai: \[ x^2 - 2x - 9 = 0 \]
- Bước 3: Tìm nghiệm của phương trình: \[ \Delta = (-2)^2 - 4 \times 1 \times (-9) = 40 \Rightarrow x = \frac{2 \pm \sqrt{40}}{2} \] Vậy nghiệm là \( x = 1 + \sqrt{10} \) hoặc \( x = 1 - \sqrt{10} \).
- Bước 4: Kiểm tra nghiệm: Chỉ nghiệm \( x = 1 + \sqrt{10} \) thỏa mãn điều kiện của logarit. Do đó, đây là nghiệm của phương trình.
Bài tập tự luyện
Hãy thử giải các phương trình logarit sau:
- \( \log_5{(2x + 3)} = 1 \)
- \( \log_7{(x^2 - 4)} = 2 \)
- \( \log_{10}{(3x + 7)} = \log_{10}{(5x - 1)} \)
Bài Tập 7: Dãy Số Và Cấp Số
Trong toán học, dãy số và cấp số là hai khái niệm quan trọng được sử dụng để mô tả các chuỗi số liên tiếp theo một quy luật nhất định. Để giải quyết các bài tập liên quan đến dãy số và cấp số, chúng ta cần nắm vững các công thức và phương pháp tính toán.
1. Dãy Số
Dãy số là một tập hợp các số được sắp xếp theo một trật tự nhất định. Một dãy số có thể được định nghĩa bằng công thức tổng quát cho mỗi phần tử trong dãy.
Ví dụ: Dãy số tự nhiên:
2. Cấp Số Cộng
Cấp số cộng là một dãy số trong đó hiệu giữa hai số liên tiếp là một hằng số. Hằng số này được gọi là công sai \(d\).
Công thức tính số hạng tổng quát của cấp số cộng:
Trong đó:
- \(a_n\): Số hạng thứ n
- \(a_1\): Số hạng đầu tiên
- \(d\): Công sai
3. Cấp Số Nhân
Cấp số nhân là một dãy số trong đó tỷ số giữa hai số liên tiếp là một hằng số. Hằng số này được gọi là công bội \(q\).
Công thức tính số hạng tổng quát của cấp số nhân:
Trong đó:
- \(a_n\): Số hạng thứ n
- \(a_1\): Số hạng đầu tiên
- \(q\): Công bội
4. Bài Tập Ví Dụ
Bài toán: Tìm số hạng thứ 10 của một cấp số cộng với \(a_1 = 3\) và \(d = 5\).
Giải:
Số hạng thứ 10 của cấp số cộng này là 48.
Bài toán: Tìm số hạng thứ 5 của một cấp số nhân với \(a_1 = 2\) và \(q = 3\).
Giải:
Số hạng thứ 5 của cấp số nhân này là 162.
Như vậy, việc nắm vững các công thức và quy tắc cơ bản sẽ giúp chúng ta dễ dàng giải quyết các bài tập liên quan đến dãy số và cấp số.
Bài Tập 8: Hình Học Không Gian
Trong phần này, chúng ta sẽ tìm hiểu về cách giải quyết các bài toán hình học không gian, bao gồm các khái niệm cơ bản như đường thẳng, mặt phẳng, khối đa diện, và cách tính thể tích của các khối hình học.
1. Định nghĩa và khái niệm cơ bản
Hình học không gian là một nhánh của hình học nghiên cứu về các hình khối ba chiều, bao gồm:
- Điểm: Một vị trí xác định trong không gian, không có kích thước.
- Đường thẳng: Tập hợp các điểm nối liền với nhau theo một hướng xác định và kéo dài vô hạn ở cả hai chiều.
- Mặt phẳng: Tập hợp các điểm tạo thành một bề mặt phẳng kéo dài vô hạn theo mọi hướng trong không gian.
- Khối đa diện: Một hình ba chiều được giới hạn bởi các mặt phẳng, chẳng hạn như khối lập phương, khối tứ diện.
2. Phương pháp giải bài toán hình học không gian
- Xác định các yếu tố cơ bản: đường thẳng, mặt phẳng, và khối đa diện trong bài toán.
- Vẽ hình minh họa: Vẽ sơ đồ hình học của bài toán để dễ dàng quan sát và hình dung các yếu tố liên quan.
- Áp dụng các công thức hình học không gian: Sử dụng các công thức tính diện tích, thể tích để giải quyết bài toán. Ví dụ:
- Thể tích khối lập phương: \[ V = a^3 \]
- Thể tích khối chóp: \[ V = \frac{1}{3} \times B \times h \]
- Thể tích khối cầu: \[ V = \frac{4}{3} \pi r^3 \]
3. Ví dụ minh họa
Xét bài toán tính thể tích của một khối lăng trụ tam giác có diện tích đáy \(B = 20 \, cm^2\) và chiều cao \(h = 15 \, cm\). Thể tích khối lăng trụ sẽ được tính như sau:
\[ V = B \times h = 20 \times 15 = 300 \, cm^3 \]
Với các bước làm này, bạn có thể dễ dàng giải quyết các bài toán liên quan đến hình học không gian.
Bài Tập 9: Tính Giá Trị Lượng Giác
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính giá trị của các hàm số lượng giác thông qua các bước cụ thể. Dưới đây là quy trình từng bước để giải quyết các bài toán liên quan đến giá trị lượng giác.
-
Nhớ lại các giá trị cơ bản của hàm lượng giác:
Trước hết, bạn cần ghi nhớ các giá trị cơ bản của các hàm số lượng giác như \(\sin\), \(\cos\), \(\tan\), \(\cot\) ở các góc đặc biệt như \(0^\circ\), \(30^\circ\), \(45^\circ\), \(60^\circ\), \(90^\circ\).
-
Sử dụng các công thức lượng giác:
Các công thức cơ bản như công thức cộng, công thức nhân đôi, công thức hạ bậc có thể được áp dụng để tính toán giá trị của các hàm số lượng giác trong những bài toán phức tạp hơn.
Ví dụ: \(\sin(2x) = 2\sin(x)\cos(x)\) hoặc \(\cos(2x) = \cos^2(x) - \sin^2(x)\).
-
Sử dụng công cụ máy tính:
Trong các bài toán yêu cầu tính giá trị chính xác đến một số thập phân cụ thể, bạn có thể sử dụng máy tính cầm tay hoặc phần mềm để tính toán. Tuy nhiên, hãy chắc chắn rằng bạn hiểu rõ các bước và chỉ sử dụng công cụ này để kiểm tra kết quả.
-
Giải ví dụ cụ thể:
Hãy cùng giải quyết một ví dụ cụ thể để minh họa:
Ví dụ: Tính giá trị của \(\sin(45^\circ) + \cos(30^\circ)\).
Lời giải:
\(\sin(45^\circ) = \frac{\sqrt{2}}{2}\) và \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\).
Do đó, \(\sin(45^\circ) + \cos(30^\circ) = \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2}\).
Kết quả cuối cùng là một số thập phân cụ thể sau khi tính toán.
Hãy luyện tập nhiều hơn với các bài toán khác nhau để thành thạo kỹ năng tính giá trị lượng giác.
Bài Tập 10: Giải Bài Toán Thực Tế
Giải bài toán thực tế thường đòi hỏi sự kết hợp giữa lý thuyết và kỹ năng phân tích để áp dụng vào các tình huống thực tiễn. Dưới đây là hướng dẫn chi tiết để giải bài toán thực tế một cách hiệu quả.
- Xác định vấn đề:
Bước đầu tiên là hiểu rõ yêu cầu của bài toán. Bạn cần đọc kỹ đề bài và xác định những yếu tố liên quan, như các đại lượng cần tính, các điều kiện và giới hạn đã cho.
- Thiết lập mô hình toán học:
Sau khi hiểu rõ vấn đề, bạn cần chuyển đổi nó thành mô hình toán học. Điều này có thể bao gồm việc sử dụng các phương trình, bất phương trình, hoặc các biểu thức khác để mô tả mối quan hệ giữa các đại lượng.
- Giải mô hình:
Sử dụng các phương pháp toán học thích hợp để giải mô hình. Điều này có thể yêu cầu bạn thực hiện các phép biến đổi, giải phương trình hoặc bất phương trình, và sử dụng các công cụ như đạo hàm, tích phân, hoặc các công thức lượng giác.
- Kiểm tra và giải thích kết quả:
Sau khi có kết quả, hãy kiểm tra lại xem nó có hợp lý và đúng với thực tế không. Bạn cần đưa ra lời giải thích rõ ràng về ý nghĩa của kết quả và cách nó giải quyết vấn đề đã nêu.
Ví dụ, nếu bạn được yêu cầu tính toán chi phí sản xuất cho một công ty dựa trên số lượng sản phẩm sản xuất, bạn có thể thiết lập một phương trình để mô tả mối quan hệ giữa chi phí và số lượng. Sau đó, bạn giải phương trình này để tìm ra số lượng sản phẩm tối ưu giúp giảm thiểu chi phí.
Phương pháp này không chỉ giúp bạn giải quyết các vấn đề toán học mà còn phát triển kỹ năng tư duy logic và khả năng áp dụng kiến thức vào thực tiễn.