Chủ đề lịch thi đấu bóng đá vòng bán kết: Lịch thi đấu bóng đá vòng bán kết đang trở thành tâm điểm chú ý của người hâm mộ toàn cầu. Trong bài viết này, chúng tôi sẽ cập nhật chi tiết các trận đấu, thời gian, và thông tin quan trọng nhất để bạn không bỏ lỡ bất kỳ diễn biến nào. Hãy cùng khám phá những trận cầu đỉnh cao sắp diễn ra!
Mục lục
- Lịch Thi Đấu Bóng Đá Vòng Bán Kết
- Lịch thi đấu vòng bán kết Euro 2024
- Lịch thi đấu vòng bán kết Asian Cup 2023
- Lịch thi đấu vòng bán kết SEA Games 32
- Lịch thi đấu vòng bán kết Olympic Paris 2024
- Lịch thi đấu vòng bán kết Cúp C1 Châu Âu 2024
- 10 Dạng Bài Tập Toán về Phương Trình Bậc Hai
- Bài tập 1: Giải phương trình bậc hai dạng cơ bản
- Bài tập 2: Tìm nghiệm của phương trình bậc hai bằng phương pháp phân tích nhân tử
- Bài tập 3: Phương pháp hoàn thành bình phương
- Bài tập 4: Sử dụng công thức nghiệm của phương trình bậc hai
- Bài tập 5: Giải và biện luận phương trình bậc hai
- Bài tập 6: Phương trình bậc hai với tham số
- Bài tập 7: Giải phương trình bậc hai có hệ số phức
- Bài tập 8: Tìm khoảng nghiệm của phương trình bậc hai
- Bài tập 9: Giải phương trình bậc hai bằng máy tính
- Bài tập 10: Ứng dụng phương trình bậc hai trong bài toán thực tế
Lịch Thi Đấu Bóng Đá Vòng Bán Kết
Dưới đây là tổng hợp lịch thi đấu vòng bán kết của một số giải đấu bóng đá nổi bật:
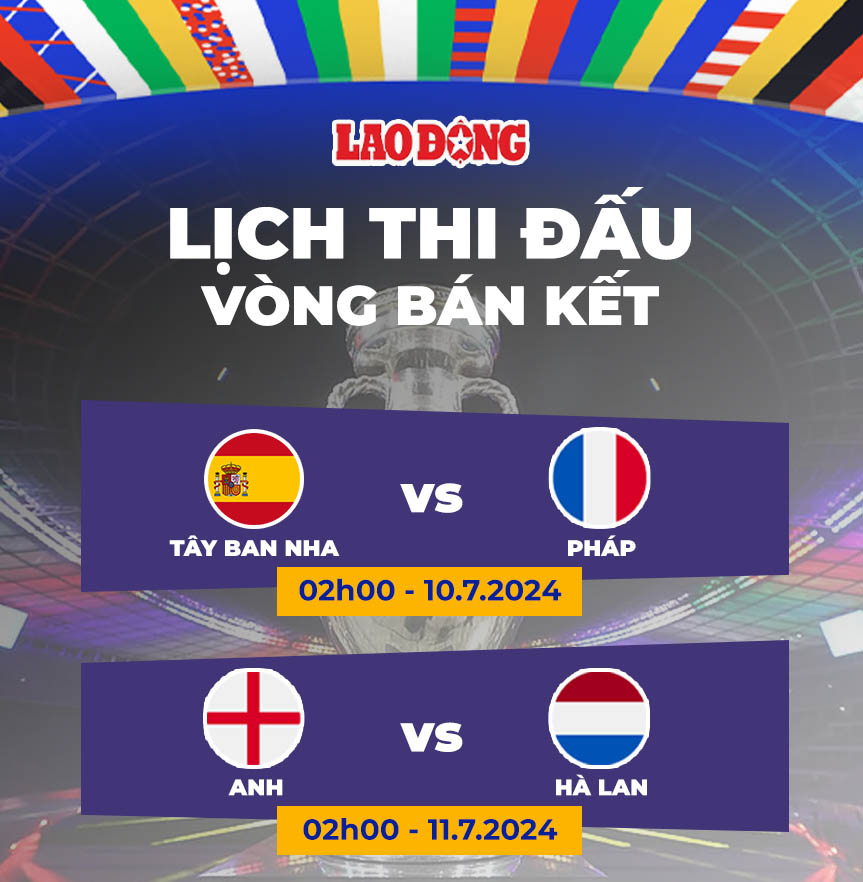
1. Bán Kết Euro 2024
- Trận 1: Diễn ra vào ngày ngày 9 tháng 7, 2024, giữa Đội tuyển A và Đội tuyển B.
- Trận 2: Diễn ra vào ngày ngày 10 tháng 7, 2024, giữa Đội tuyển C và Đội tuyển D.
2. Bán Kết Asian Cup 2023
- Trận 1: Ngày ngày 15 tháng 8, 2023, giữa U23 Nhật Bản và U23 Hàn Quốc.
- Trận 2: Ngày ngày 16 tháng 8, 2023, giữa U23 Việt Nam và U23 Thái Lan.
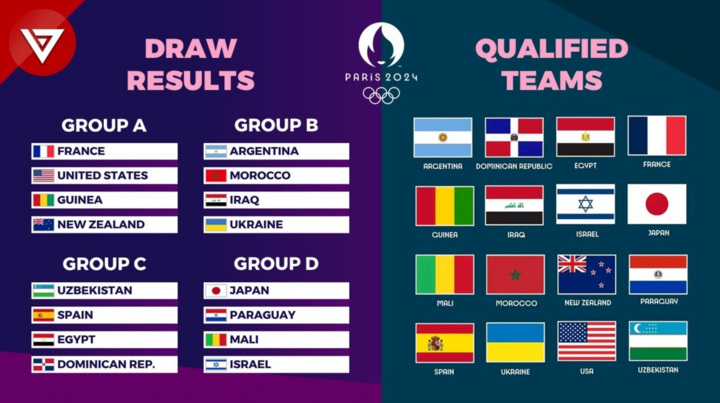
3. Bán Kết Môn Bóng Đá Nam - Olympic Paris 2024
- Trận 1: Diễn ra vào ngày 7 tháng 8, 2024, giữa Pháp và Tây Ban Nha.
- Trận 2: Diễn ra vào ngày 8 tháng 8, 2024, giữa Brazil và Argentina.
4. Bán Kết SEA Games 32
- Trận 1: Ngày ngày 10 tháng 5, 2023, giữa U22 Việt Nam và U22 Indonesia.
- Trận 2: Ngày ngày 11 tháng 5, 2023, giữa U22 Thái Lan và U22 Myanmar.
Các trận đấu này đều rất được mong đợi, với những đội bóng hàng đầu khu vực và thế giới tham gia tranh tài, hứa hẹn mang đến những trận đấu kịch tính và hấp dẫn.
.png)
Lịch thi đấu vòng bán kết Euro 2024
Euro 2024 hứa hẹn sẽ mang đến những trận cầu hấp dẫn tại vòng bán kết, nơi các đội bóng mạnh nhất châu Âu sẽ so tài để giành vé vào chung kết. Dưới đây là lịch thi đấu chi tiết của vòng bán kết:
| Ngày | Giờ (CET) | Trận đấu | Địa điểm |
|---|---|---|---|
| 9 tháng 7, 2024 | 21:00 | Đội tuyển A vs Đội tuyển B | Sân vận động Allianz Arena, Munich |
| 10 tháng 7, 2024 | 21:00 | Đội tuyển C vs Đội tuyển D | Sân vận động Wembley, London |
Trận bán kết đầu tiên sẽ diễn ra tại Allianz Arena ở Munich, nơi đội tuyển A sẽ đối đầu với đội tuyển B. Trong khi đó, trận bán kết thứ hai sẽ được tổ chức tại Wembley, sân vận động huyền thoại ở London, nơi đội tuyển C sẽ gặp đội tuyển D.
Các đội bóng đang chuẩn bị kỹ lưỡng cho những trận đấu quan trọng này, với mục tiêu cuối cùng là chiếc cúp danh giá Euro 2024. Hãy theo dõi và cổ vũ cho đội bóng bạn yêu thích!
Lịch thi đấu vòng bán kết Asian Cup 2023
Asian Cup 2023 đang đến giai đoạn gay cấn với vòng bán kết, nơi các đội tuyển xuất sắc nhất châu Á sẽ tranh tài để tiến tới trận chung kết. Dưới đây là lịch thi đấu chi tiết của vòng bán kết:
| Ngày | Giờ (CET) | Trận đấu | Địa điểm |
|---|---|---|---|
| 15 tháng 8, 2023 | 20:00 | U23 Nhật Bản vs U23 Hàn Quốc | Sân vận động Quốc gia, Tokyo |
| 16 tháng 8, 2023 | 20:00 | U23 Việt Nam vs U23 Thái Lan | Sân vận động Mỹ Đình, Hà Nội |
Trận bán kết đầu tiên sẽ diễn ra tại Sân vận động Quốc gia ở Tokyo, với cuộc đối đầu giữa U23 Nhật Bản và U23 Hàn Quốc. Đây là trận đấu đầy duyên nợ giữa hai nền bóng đá mạnh nhất khu vực Đông Á.
Trận bán kết thứ hai sẽ diễn ra tại Sân vận động Mỹ Đình, Hà Nội, nơi U23 Việt Nam sẽ chạm trán với U23 Thái Lan. Cuộc đối đầu này hứa hẹn sẽ rất kịch tính khi hai đội bóng có phong độ ấn tượng tại giải đấu lần này.
Các trận đấu đều rất đáng mong đợi và sẽ quyết định những gương mặt cuối cùng bước vào trận chung kết tranh ngôi vương tại Asian Cup 2023.

Lịch thi đấu vòng bán kết SEA Games 32
SEA Games 32 đang đến gần với những trận cầu đỉnh cao tại vòng bán kết môn bóng đá nam. Đây là thời điểm các đội bóng mạnh nhất khu vực Đông Nam Á tranh tài để giành tấm vé vào trận chung kết. Dưới đây là lịch thi đấu chi tiết của vòng bán kết:
| Ngày | Giờ (CET) | Trận đấu | Địa điểm |
|---|---|---|---|
| 10 tháng 5, 2023 | 18:00 | U22 Việt Nam vs U22 Indonesia | Sân vận động Morodok Techo, Phnom Penh |
| 11 tháng 5, 2023 | 18:00 | U22 Thái Lan vs U22 Myanmar | Sân vận động Olympic, Phnom Penh |
Trận bán kết đầu tiên sẽ diễn ra vào ngày 10 tháng 5, 2023 tại Sân vận động Morodok Techo, Phnom Penh, với cuộc đối đầu giữa U22 Việt Nam và U22 Indonesia. Đây là trận đấu hứa hẹn sẽ rất kịch tính khi hai đội bóng đều thể hiện phong độ ấn tượng từ đầu giải.
Ngày hôm sau, 11 tháng 5, 2023, U22 Thái Lan sẽ gặp U22 Myanmar tại Sân vận động Olympic, Phnom Penh. Trận đấu này sẽ xác định đội bóng thứ hai góp mặt trong trận chung kết, nơi sự quyết tâm và tài năng của các cầu thủ trẻ sẽ được thử thách đến cùng.
Vòng bán kết SEA Games 32 không chỉ là nơi để các đội tuyển tranh tài mà còn là dịp để các cổ động viên Đông Nam Á thể hiện tình yêu bóng đá và sự đoàn kết khu vực.

Lịch thi đấu vòng bán kết Olympic Paris 2024
Olympic Paris 2024 đang đến gần với những trận cầu đỉnh cao tại vòng bán kết môn bóng đá nam. Các đội bóng mạnh nhất thế giới sẽ tranh tài để giành tấm vé vào trận chung kết, nơi họ sẽ chiến đấu vì vinh quang Olympic. Dưới đây là lịch thi đấu chi tiết của vòng bán kết:
| Ngày | Giờ (CET) | Trận đấu | Địa điểm |
|---|---|---|---|
| 5 tháng 8, 2024 | 21:00 | Pháp vs Tây Ban Nha | Sân vận động Parc des Princes, Paris |
| 6 tháng 8, 2024 | 21:00 | Brazil vs Argentina | Sân vận động Stade de France, Saint-Denis |
Trận bán kết đầu tiên sẽ diễn ra tại Parc des Princes ở Paris, nơi đội chủ nhà Pháp sẽ đối đầu với Tây Ban Nha, một trong những đội bóng mạnh nhất châu Âu. Trận đấu này hứa hẹn sẽ rất căng thẳng và quyết liệt khi cả hai đội đều có tham vọng lớn tại kỳ Olympic lần này.
Trận bán kết thứ hai sẽ diễn ra tại Stade de France ở Saint-Denis, nơi Brazil sẽ chạm trán với Argentina trong trận "Siêu kinh điển" của bóng đá Nam Mỹ. Đây là cuộc đối đầu được chờ đợi nhất, khi hai đội bóng với lối chơi kỹ thuật cao sẽ tranh tài để giành tấm vé cuối cùng vào chung kết.
Các trận đấu bán kết tại Olympic Paris 2024 hứa hẹn sẽ mang đến những khoảnh khắc khó quên và những bàn thắng đẹp mắt. Hãy cùng đón xem và cổ vũ cho đội bóng bạn yêu thích!

Lịch thi đấu vòng bán kết Cúp C1 Châu Âu 2024
Cúp C1 Châu Âu 2024 đang đến giai đoạn kịch tính với vòng bán kết, nơi các câu lạc bộ hàng đầu châu Âu sẽ tranh tài để giành vé vào trận chung kết danh giá. Dưới đây là lịch thi đấu chi tiết của vòng bán kết:
| Ngày | Giờ (CET) | Trận đấu | Địa điểm |
|---|---|---|---|
| 23 tháng 4, 2024 | 20:00 | Manchester City vs Real Madrid | Sân vận động Etihad, Manchester |
| 24 tháng 4, 2024 | 20:00 | Bayern Munich vs Liverpool | Sân vận động Allianz Arena, Munich |
| 30 tháng 4, 2024 | 20:00 | Real Madrid vs Manchester City | Sân vận động Santiago Bernabéu, Madrid |
| 1 tháng 5, 2024 | 20:00 | Liverpool vs Bayern Munich | Sân vận động Anfield, Liverpool |
Trận bán kết đầu tiên sẽ diễn ra vào ngày 23 tháng 4, 2024 tại Etihad, Manchester, khi Manchester City đón tiếp Real Madrid. Trận lượt về sẽ diễn ra vào 30 tháng 4, 2024 tại Santiago Bernabéu, Madrid.
Trận bán kết thứ hai sẽ diễn ra vào ngày 24 tháng 4, 2024 tại Allianz Arena, Munich, nơi Bayern Munich sẽ đối đầu với Liverpool. Trận lượt về sẽ diễn ra vào 1 tháng 5, 2024 tại Anfield, Liverpool.
Các trận đấu bán kết của Cúp C1 Châu Âu 2024 sẽ là những cuộc đối đầu đầy hấp dẫn, với những câu lạc bộ danh tiếng và những ngôi sao sáng giá. Hãy cùng đón xem và ủng hộ đội bóng mà bạn yêu thích!
XEM THÊM:
10 Dạng Bài Tập Toán về Phương Trình Bậc Hai
Phương trình bậc hai là một trong những chủ đề quan trọng trong toán học, thường xuyên xuất hiện trong các kỳ thi. Dưới đây là 10 dạng bài tập phổ biến về phương trình bậc hai mà học sinh cần nắm vững.
Bài tập 1: Giải phương trình bậc hai dạng cơ bản
Phương trình bậc hai cơ bản có dạng:
\[ ax^2 + bx + c = 0 \]
Trong đó, \(a\), \(b\), và \(c\) là các hệ số. Để giải phương trình này, học sinh có thể sử dụng công thức nghiệm:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Bài tập 2: Tìm nghiệm của phương trình bậc hai bằng phương pháp phân tích nhân tử
Bước 1: Xác định hai số \(m\) và \(n\) sao cho:
\[ m \times n = a \times c \quad \text{và} \quad m + n = b \]
Bước 2: Phân tích phương trình ban đầu thành:
\[ ax^2 + mx + nx + c = 0 \]
Bước 3: Nhóm các hạng tử và phân tích nhân tử chung:
\[ (ax + m)(x + n/a) = 0 \]
Bài tập 3: Phương pháp hoàn thành bình phương
Phương pháp này biến đổi phương trình bậc hai về dạng:
\[ (x + p)^2 = q \]
Ví dụ, với phương trình:
\[ x^2 + 6x + 5 = 0 \]
Hoàn thành bình phương thành:
\[ (x + 3)^2 = 4 \]
Giải ra nghiệm của phương trình:
\[ x = -3 \pm 2 \]
Bài tập 4: Sử dụng công thức nghiệm của phương trình bậc hai
Công thức nghiệm tổng quát của phương trình bậc hai được sử dụng trong hầu hết các trường hợp:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Áp dụng công thức này cho các giá trị cụ thể của \(a\), \(b\), và \(c\).
Bài tập 5: Giải và biện luận phương trình bậc hai
Biện luận nghiệm dựa trên giá trị của delta (\(\Delta\)):
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có một nghiệm kép.
- Nếu \(\Delta < 0\), phương trình vô nghiệm thực.
Bài tập 6: Phương trình bậc hai với tham số
Phương trình bậc hai với tham số có dạng:
\[ ax^2 + bx + c = 0 \]
Trong đó \(a\), \(b\), hoặc \(c\) là các biểu thức chứa tham số. Giải phương trình này thường yêu cầu biện luận theo tham số.
Bài tập 7: Giải phương trình bậc hai có hệ số phức
Phương trình có hệ số phức có dạng:
\[ z^2 + (a + bi)z + c = 0 \]
Trong đó \(i\) là đơn vị ảo. Nghiệm của phương trình được tìm bằng cách sử dụng công thức bậc hai và giải quyết trong trường số phức.
Bài tập 8: Tìm khoảng nghiệm của phương trình bậc hai
Xác định khoảng nghiệm bằng cách xét dấu của biểu thức:
\[ ax^2 + bx + c = 0 \]
Dựa trên tính chất của hàm số bậc hai, xác định khoảng nghiệm trong các khoảng giá trị cụ thể của \(x\).
Bài tập 9: Giải phương trình bậc hai bằng máy tính
Sử dụng máy tính cầm tay để giải phương trình bậc hai một cách nhanh chóng và chính xác.
- Bước 1: Nhập các hệ số \(a\), \(b\), \(c\).
- Bước 2: Sử dụng chức năng giải phương trình của máy tính.
- Bước 3: Đọc kết quả nghiệm trên màn hình.
Bài tập 10: Ứng dụng phương trình bậc hai trong bài toán thực tế
Phương trình bậc hai có nhiều ứng dụng trong thực tế như:
- Tính toán quỹ đạo của vật thể.
- Phân tích tài chính, tối ưu hóa lợi nhuận.
- Dự đoán xu hướng, lập kế hoạch.

Bài tập 1: Giải phương trình bậc hai dạng cơ bản
Phương trình bậc hai có dạng tổng quát:
Trong đó:
- a, b, c là các hằng số, với a ≠ 0.
- x là ẩn số cần tìm.
Để giải phương trình bậc hai, chúng ta sử dụng công thức nghiệm:
Quy trình giải phương trình bậc hai gồm các bước sau:
- Xác định các hệ số a, b, c từ phương trình đã cho.
- Tính ∆ (Delta) theo công thức: \[ ∆ = b^2 - 4ac \]
- Phân loại nghiệm dựa trên giá trị của ∆:
- Nếu \(∆ > 0\), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{-b + \sqrt{∆}}{2a}, \quad x_2 = \frac{-b - \sqrt{∆}}{2a} \]
- Nếu \(∆ = 0\), phương trình có nghiệm kép: \[ x = \frac{-b}{2a} \]
- Nếu \(∆ < 0\), phương trình vô nghiệm thực.
- Viết kết luận về nghiệm của phương trình.
Ví dụ: Giải phương trình \(2x^2 - 4x + 2 = 0\).
- Xác định các hệ số: \(a = 2\), \(b = -4\), \(c = 2\).
- Tính \(∆\): \[ ∆ = (-4)^2 - 4 \cdot 2 \cdot 2 = 16 - 16 = 0 \]
- Vì \(∆ = 0\), phương trình có nghiệm kép: \[ x = \frac{-(-4)}{2 \cdot 2} = \frac{4}{4} = 1 \]
- Kết luận: Phương trình có nghiệm kép \(x = 1\).

Bài tập 2: Tìm nghiệm của phương trình bậc hai bằng phương pháp phân tích nhân tử
Phương pháp phân tích nhân tử là một cách phổ biến để tìm nghiệm của phương trình bậc hai. Phương trình bậc hai có dạng tổng quát:
\[ ax^2 + bx + c = 0 \]
Để giải phương trình này bằng phương pháp phân tích nhân tử, chúng ta làm theo các bước sau:
- Bước 1: Tìm hai số m và n sao cho:
- \( m \times n = a \times c \) (tích của hệ số bậc hai và hệ số tự do)
- \( m + n = b \) (tổng của hai số bằng hệ số bậc nhất)
- Bước 2: Phân tích trung bình cộng:
- Bước 3: Nhóm các hạng tử:
- Bước 4: Giải phương trình tích:
- \( ax + m = 0 \)
- \( x + n = 0 \)
Thay \( bx \) bằng \( mx + nx \) trong phương trình:
\[ ax^2 + mx + nx + c = 0 \]
Nhóm các hạng tử thành từng cặp và đặt nhân tử chung:
\[ (ax + m)(x + n) = 0 \]
Sử dụng định lý nhân tử không để giải hai phương trình đơn:
Kết quả sẽ là hai nghiệm của phương trình.
Ví dụ: Giải phương trình \( 2x^2 + 5x + 3 = 0 \) bằng phương pháp phân tích nhân tử.
Giải:
- Bước 1: Tìm hai số m và n:
- \( m \times n = 2 \times 3 = 6 \)
- \( m + n = 5 \) (Hai số cần tìm là 2 và 3)
- Bước 2: Phân tích trung bình cộng:
- Bước 3: Nhóm các hạng tử:
- Bước 4: Giải phương trình tích:
- \( 2x + 3 = 0 \rightarrow x = -\frac{3}{2} \)
- \( x + 1 = 0 \rightarrow x = -1 \)
Thay 5x bằng 2x và 3x:
\[ 2x^2 + 2x + 3x + 3 = 0 \]
Nhóm và đặt nhân tử chung:
\[ 2x(x + 1) + 3(x + 1) = 0 \]
Ta có hai phương trình:
Vậy nghiệm của phương trình là \( x = -\frac{3}{2} \) và \( x = -1 \).
Bài tập 3: Phương pháp hoàn thành bình phương
Phương pháp hoàn thành bình phương là một kỹ thuật hữu ích để giải phương trình bậc hai. Để sử dụng phương pháp này, chúng ta sẽ thêm và bớt một giá trị thích hợp vào phương trình để biến đổi nó thành một bình phương hoàn hảo.
- Bước 1: Xác định phương trình bậc hai tổng quát
Phương trình bậc hai có dạng tổng quát là:
\[ ax^2 + bx + c = 0 \]
Trong đó, \(a\), \(b\), và \(c\) là các hệ số đã cho.
- Bước 2: Chia phương trình cho hệ số của \(x^2\)
Để đơn giản, chia cả hai vế của phương trình cho \(a\) (giả sử \(a \neq 0\)):
\[ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \]
- Bước 3: Hoàn thành bình phương
Bước này yêu cầu bạn thêm và bớt giá trị \(\left(\frac{b}{2a}\right)^2\) vào phương trình để tạo thành một bình phương hoàn hảo:
\[ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2 + \frac{c}{a} = 0 \]
Viết lại phương trình dưới dạng:
\[ \left(x + \frac{b}{2a}\right)^2 = \left(\frac{b^2 - 4ac}{4a^2}\right) \]
- Bước 4: Giải phương trình
Cuối cùng, giải phương trình bằng cách lấy căn bậc hai hai vế và tìm giá trị của \(x\):
\[ x + \frac{b}{2a} = \pm \sqrt{\frac{b^2 - 4ac}{4a^2}} \]
Sau đó, tìm nghiệm:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Phương pháp này không chỉ giúp giải phương trình mà còn được sử dụng trong nhiều ứng dụng khác trong toán học, đặc biệt trong việc tìm đỉnh của parabol hoặc viết phương trình dưới dạng chuẩn.

Bài tập 4: Sử dụng công thức nghiệm của phương trình bậc hai
Để giải phương trình bậc hai bằng cách sử dụng công thức nghiệm, ta cần áp dụng công thức sau đây:
Cho phương trình bậc hai có dạng tổng quát:
Trong đó, \(a\), \(b\), và \(c\) là các hằng số, với \(a \neq 0\). Công thức nghiệm của phương trình này được cho bởi:
Để tìm nghiệm của phương trình bậc hai, ta thực hiện các bước sau:
- Xác định các hệ số: Từ phương trình đã cho, xác định giá trị của \(a\), \(b\), và \(c\).
- Tính giá trị của biệt thức \(\Delta\): Biệt thức \(\Delta\) được tính bằng công thức: \[ \Delta = b^2 - 4ac \]
- Xác định tính chất của nghiệm:
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có một nghiệm kép.
- Nếu \(\Delta < 0\), phương trình vô nghiệm (không có nghiệm thực).
- Tính nghiệm của phương trình: Sử dụng công thức nghiệm đã cho ở trên để tính giá trị của \(x_1\) và \(x_2\).
Ví dụ: Giải phương trình bậc hai sau đây:
Bước 1: Xác định các hệ số: \(a = 2\), \(b = -4\), \(c = -6\).
Bước 2: Tính \(\Delta\):
Bước 3: Vì \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
Bước 4: Tính nghiệm:
Vậy phương trình có hai nghiệm là \(x_1 = 3\) và \(x_2 = -1\).
Bài tập 5: Giải và biện luận phương trình bậc hai
Trong bài tập này, chúng ta sẽ tìm hiểu cách giải và biện luận phương trình bậc hai dựa trên giá trị của biệt thức \( \Delta \). Phương trình bậc hai tổng quát có dạng:
Trong đó \( a \), \( b \), và \( c \) là các hệ số với \( a \neq 0 \). Để giải và biện luận phương trình này, ta cần thực hiện các bước sau:
- Tính biệt thức \( \Delta \):
- Biện luận số nghiệm dựa trên \( \Delta \):
- Nếu \( \Delta > 0 \): Phương trình có hai nghiệm phân biệt, được tính theo công thức: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
- Nếu \( \Delta = 0 \): Phương trình có một nghiệm kép: \[ x = \frac{-b}{2a} \]
- Nếu \( \Delta < 0 \): Phương trình vô nghiệm (trong tập số thực).
- Ví dụ minh họa:
Biệt thức \( \Delta \) được tính theo công thức:
\[ \Delta = b^2 - 4ac \]Biệt thức \( \Delta \) quyết định số lượng nghiệm của phương trình.
Xét phương trình sau:
\[ 2x^2 - 4x + 2 = 0 \]Ta có:
\[ a = 2, \, b = -4, \, c = 2 \]Tính biệt thức \( \Delta \):
\[ \Delta = (-4)^2 - 4 \cdot 2 \cdot 2 = 16 - 16 = 0 \]Vì \( \Delta = 0 \), phương trình có một nghiệm kép:
\[ x = \frac{-(-4)}{2 \cdot 2} = \frac{4}{4} = 1 \]Như vậy, nghiệm của phương trình là \( x = 1 \).
Hy vọng qua bài tập này, bạn đã hiểu rõ hơn về cách giải và biện luận phương trình bậc hai dựa trên giá trị của \( \Delta \).
Bài tập 6: Phương trình bậc hai với tham số
Trong bài tập này, chúng ta sẽ nghiên cứu phương trình bậc hai với tham số và cách giải quyết nó. Phương trình bậc hai tổng quát có dạng:
Với a, b, c là các hệ số và x là ẩn số. Khi một hoặc nhiều hệ số phụ thuộc vào một tham số m, phương trình trở thành:
Để giải phương trình bậc hai với tham số, ta thực hiện các bước sau:
- Xác định điều kiện của tham số: Trước hết, cần xác định điều kiện của tham số m để phương trình là phương trình bậc hai (tức là a(m) ≠ 0).
- Sử dụng công thức nghiệm tổng quát: Khi đã có điều kiện của tham số, ta sử dụng công thức nghiệm của phương trình bậc hai: \[ x = \frac{-b(m) \pm \sqrt{b(m)^2 - 4a(m)c(m)}}{2a(m)} \]
- Biện luận nghiệm: Dựa vào biểu thức dưới căn \(\Delta = b(m)^2 - 4a(m)c(m)\), ta biện luận số nghiệm của phương trình:
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có nghiệm kép.
- Nếu \(\Delta < 0\), phương trình vô nghiệm thực.
- Kết luận: Sau khi giải, ta kết luận về nghiệm của phương trình tùy theo giá trị cụ thể của tham số m.
Ví dụ minh họa: Xét phương trình bậc hai có dạng:
Hãy giải phương trình và biện luận theo m.
Qua ví dụ này, bạn sẽ hiểu rõ hơn về cách giải và biện luận phương trình bậc hai với tham số. Hãy thử áp dụng các bước đã học để giải bài tập tương tự!

Bài tập 7: Giải phương trình bậc hai có hệ số phức
Phương trình bậc hai với hệ số phức có dạng tổng quát:
\[
az^2 + bz + c = 0
\]
với \(a\), \(b\), \(c\) là các số phức, và \(z\) là ẩn số cần tìm.
Để giải phương trình bậc hai có hệ số phức, ta có thể sử dụng công thức nghiệm của phương trình bậc hai tương tự như đối với các hệ số thực:
\[
z = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Tuy nhiên, vì \(b^2 - 4ac\) là một biểu thức có thể là số phức, việc tính toán căn bậc hai của một số phức cần được thực hiện cẩn thận. Dưới đây là các bước giải phương trình bậc hai có hệ số phức:
**Tính biệt thức** \( \Delta = b^2 - 4ac \):
- Nếu \( \Delta \) là số thực không âm, ta lấy căn bậc hai như thông thường.
- Nếu \( \Delta \) là số thực âm, kết quả sẽ là một số phức thuần ảo.
- Nếu \( \Delta \) là số phức bất kỳ, ta cần dùng công thức căn bậc hai của số phức.
**Tìm hai nghiệm** của phương trình theo công thức trên.
Lưu ý rằng, nghiệm có thể là các số phức và cần được biểu diễn dưới dạng \( x + yi \), với \( x, y \) là các số thực.
**Ví dụ:** Giải phương trình sau:
\[
z^2 + (1 + i)z + (1 - i) = 0
\]
Bước 1: Tính biệt thức:
\[
\Delta = (1 + i)^2 - 4 \times 1 \times (1 - i) = 1 + 2i + i^2 - 4 + 4i = -2 + 6i
\]
Bước 2: Tính căn bậc hai của \( \Delta \):
Do \( \Delta = -2 + 6i \), nên tính căn bậc hai của số phức này sẽ cần các công thức đặc biệt, dẫn đến hai giá trị có thể của \( \sqrt{\Delta} \).
Bước 3: Sử dụng công thức nghiệm để tìm nghiệm:
\[
z = \frac{-(1 + i) \pm \sqrt{-2 + 6i}}{2}
\]
Cuối cùng, nghiệm của phương trình là hai số phức có dạng:
\[
z_1, z_2 = x_1 + y_1i, \quad x_2 + y_2i
\]
với \( x_1, y_1, x_2, y_2 \) là các giá trị thực, được tính sau khi đã xác định căn bậc hai của \( \Delta \).
Giải phương trình bậc hai với hệ số phức đòi hỏi kỹ năng xử lý số phức tốt, đặc biệt là việc tìm căn bậc hai của số phức và biểu diễn nghiệm dưới dạng phù hợp.
Bài tập 8: Tìm khoảng nghiệm của phương trình bậc hai
Trong bài tập này, chúng ta sẽ tìm khoảng nghiệm của phương trình bậc hai bằng cách phân tích dấu của biểu thức dưới dấu căn. Để làm điều này, chúng ta sẽ xem xét phương trình bậc hai tổng quát dưới dạng:
Với các bước thực hiện như sau:
-
Bước 1: Tính biệt thức (Delta)
Biệt thức của phương trình bậc hai được tính bằng công thức:
\[ \Delta = b^2 - 4ac \]Biệt thức này sẽ giúp ta xác định số lượng và tính chất của nghiệm phương trình.
-
Bước 2: Phân tích dấu của Delta
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm thực phân biệt. Chúng ta sẽ tìm khoảng nghiệm bằng cách xác định vị trí của các nghiệm này trên trục số.
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép. Nghiệm này sẽ là một giá trị duy nhất và không cần tìm khoảng.
- Nếu \(\Delta < 0\): Phương trình không có nghiệm thực. Trong trường hợp này, không tồn tại khoảng nghiệm trên trục số thực.
-
Bước 3: Xác định khoảng nghiệm
Khi \(\Delta > 0\), hai nghiệm của phương trình có thể được xác định bằng:
\[ x_1 = \frac{-b - \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b + \sqrt{\Delta}}{2a} \]Khoảng nghiệm của phương trình sẽ là \((x_1, x_2)\) hoặc \((x_2, x_1)\) tùy thuộc vào thứ tự của các nghiệm. Đoạn này sẽ biểu thị khoảng các giá trị của \(x\) mà phương trình có nghiệm.
Việc xác định khoảng nghiệm là một phần quan trọng trong việc phân tích và hiểu sâu hơn về đặc tính của các phương trình bậc hai. Để nắm vững phương pháp này, bạn cần thực hành với nhiều bài tập khác nhau.
Bài tập 9: Giải phương trình bậc hai bằng máy tính
Trong bài tập này, chúng ta sẽ học cách sử dụng máy tính cầm tay để giải phương trình bậc hai, cụ thể là sử dụng máy tính CASIO fx-570VN Plus, một trong những loại máy tính phổ biến nhất hiện nay. Các bước thực hiện như sau:
- Bước 1: Bật máy tính và chuyển sang chế độ giải phương trình bậc hai
Nhấn phím
MODE, sau đó chọn5: EQNvà tiếp theo chọn3: ax^2+bx+c=0. Máy tính sẽ chuyển sang chế độ giải phương trình bậc hai với ba hệ số a, b, c. - Bước 2: Nhập các hệ số của phương trình
Nhập lần lượt các giá trị của a, b, và c theo thứ tự yêu cầu của máy tính.
- Nhập giá trị của a và nhấn
= - Nhập giá trị của b và nhấn
= - Nhập giá trị của c và nhấn
=
- Nhập giá trị của a và nhấn
- Bước 3: Xem kết quả
Sau khi nhập đủ các hệ số, máy tính sẽ hiển thị nghiệm của phương trình. Nếu phương trình có hai nghiệm, chúng sẽ được hiển thị lần lượt dưới dạng x1 và x2. Nếu phương trình có nghiệm kép, máy tính sẽ chỉ hiển thị một nghiệm.
- Bước 4: Kiểm tra kết quả
Để chắc chắn rằng kết quả là chính xác, bạn có thể thử thay giá trị nghiệm vừa tìm được vào phương trình ban đầu và kiểm tra xem phương trình có thỏa mãn hay không.
Bằng cách này, bạn có thể dễ dàng giải các phương trình bậc hai phức tạp mà không cần phải thực hiện các phép toán tay. Đây là một công cụ hữu ích giúp tiết kiệm thời gian và giảm thiểu sai sót trong quá trình tính toán.

Bài tập 10: Ứng dụng phương trình bậc hai trong bài toán thực tế
Phương trình bậc hai không chỉ là một phần quan trọng trong toán học lý thuyết mà còn có nhiều ứng dụng trong các bài toán thực tế, từ việc tính toán thời gian di chuyển, tối ưu hóa chi phí, đến dự đoán quỹ đạo chuyển động.
Một trong những ứng dụng phổ biến của phương trình bậc hai là trong việc dự đoán vị trí và vận tốc của một vật thể chuyển động dưới tác động của trọng lực, chẳng hạn như trong thể thao khi tính toán quỹ đạo của một quả bóng đá.
Ví dụ 1: Dự đoán quỹ đạo của một quả bóng đá
Giả sử bạn muốn tính toán quỹ đạo của một quả bóng đá được sút lên từ mặt đất với vận tốc ban đầu \(v_0\) và góc sút so với mặt đất là \(\theta\).
Phương trình quỹ đạo của quả bóng có dạng:
Trong đó:
- \(y\) là độ cao của quả bóng tại vị trí \(x\).
- \(\theta\) là góc sút.
- \(v_0\) là vận tốc ban đầu.
- \(g\) là gia tốc trọng trường, thường lấy giá trị \(9.8 \, m/s^2\).
Với công thức này, bạn có thể xác định được chiều cao tối đa mà quả bóng đạt được cũng như khoảng cách mà nó có thể bay xa.
Ví dụ 2: Tối ưu hóa chi phí sản xuất
Trong kinh tế học, phương trình bậc hai thường được sử dụng để mô hình hóa mối quan hệ giữa chi phí sản xuất và số lượng sản phẩm. Giả sử chi phí sản xuất được mô tả bởi phương trình:
Trong đó:
- \(C(x)\) là chi phí sản xuất tổng cộng khi sản xuất \(x\) đơn vị sản phẩm.
- \(a\), \(b\), và \(c\) là các hằng số xác định dựa trên điều kiện sản xuất cụ thể.
Bằng cách giải phương trình bậc hai này, nhà sản xuất có thể tìm ra số lượng sản phẩm cần sản xuất để tối thiểu hóa chi phí hoặc đạt được lợi nhuận tối đa.
Những ứng dụng này cho thấy sức mạnh của phương trình bậc hai trong việc giải quyết các vấn đề thực tiễn và tối ưu hóa các hoạt động trong nhiều lĩnh vực khác nhau.