Chủ đề lịch thi đấu bóng đá việt nam u20: Lịch thi đấu bóng đá Việt Nam U20 là tâm điểm chú ý của người hâm mộ khi đội tuyển trẻ Việt Nam tham gia các giải đấu quốc tế. Bài viết này sẽ cung cấp đầy đủ và chi tiết nhất về lịch thi đấu, kết quả, cũng như những thông tin bên lề thú vị, giúp bạn không bỏ lỡ bất kỳ trận đấu nào của U20 Việt Nam.
Mục lục
- Lịch Thi Đấu Bóng Đá Việt Nam U20
- Mục Lục Tổng Hợp Nội Dung
- 1. Lịch Thi Đấu Vòng Chung Kết U20 Châu Á 2023
- 2. Thông Tin Về Đội Tuyển U20 Việt Nam
- 3. Đối Thủ Của U20 Việt Nam
- 4. Các Trận Đấu Giao Hữu Trước Giải
- 5. Thông Tin Bên Lề Giải Đấu
- 6. Phân Tích Và Dự Đoán Kết Quả Giải Đấu
- 7. Lời Khuyên Cho Người Hâm Mộ
- 10 Dạng Bài Tập Toán Học Có Lời Giải
- Dạng 1: Phương Trình Bậc Hai Một Ẩn
- Dạng 2: Hệ Phương Trình Tuyến Tính
- Dạng 3: Giải Bất Đẳng Thức
- Dạng 4: Tính Toán Với Số Phức
- Dạng 5: Phương Trình Lượng Giác
- Dạng 6: Đạo Hàm và Ứng Dụng
- Dạng 7: Tích Phân Cơ Bản
- Dạng 8: Ứng Dụng Của Hình Học Giải Tích
- Dạng 9: Bài Toán Tổ Hợp
- Dạng 10: Xác Suất Thống Kê
Lịch Thi Đấu Bóng Đá Việt Nam U20
Đội tuyển U20 Việt Nam đã và đang có những trận đấu đầy kịch tính tại vòng chung kết U20 châu Á 2023. Đây là giải đấu thu hút sự chú ý lớn từ người hâm mộ trong nước cũng như quốc tế. Dưới đây là chi tiết về lịch thi đấu của đội tuyển.
Lịch Thi Đấu Vòng Bảng
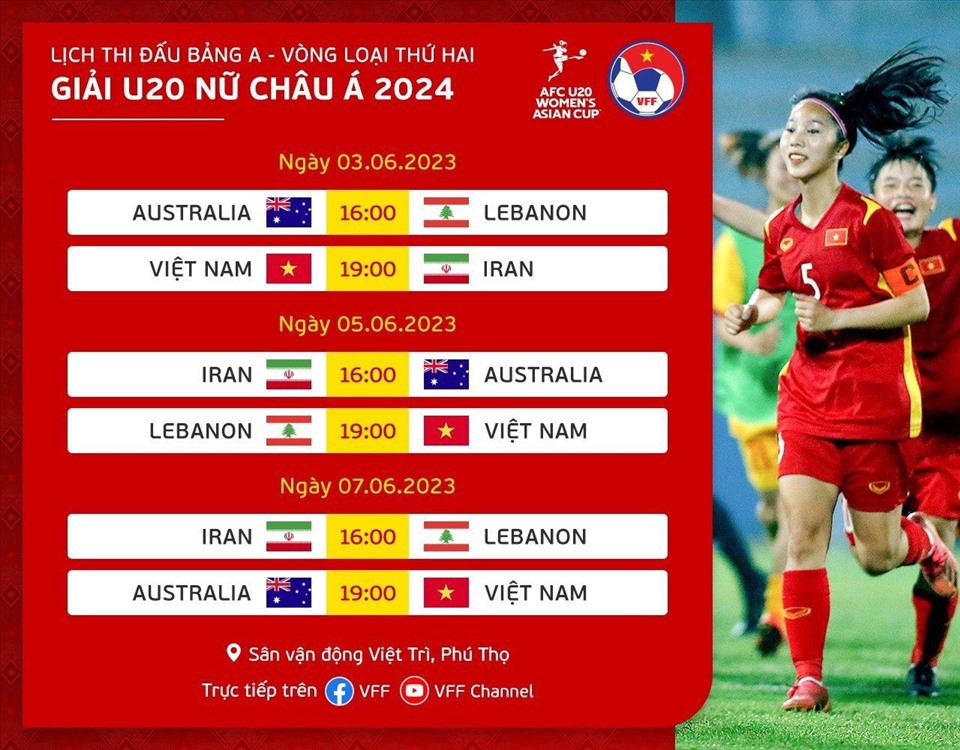
- Ngày 1/3: U20 Việt Nam vs U20 Australia (17:00)
- Ngày 4/3: U20 Việt Nam vs U20 Qatar (21:00)
- Ngày 7/3: U20 Việt Nam vs U20 Iran (17:00)
Thông Tin Chung
Vòng chung kết U20 châu Á 2023 được tổ chức tại Uzbekistan từ ngày 1 đến 18 tháng 3 năm 2023. Đội tuyển U20 Việt Nam nằm trong bảng B cùng với các đối thủ mạnh như Australia, Qatar và Iran.
Đội tuyển Việt Nam sẽ thi đấu với mật độ 3 ngày một trận, và tất cả các trận đấu của U20 Việt Nam trong vòng bảng sẽ diễn ra trên sân Istiqlol, tỉnh Fergana.
Kết Quả Các Trận Đấu
- U20 Việt Nam 1-0 U20 Australia: Một chiến thắng đầy bất ngờ và kịch tính với pha làm bàn đẹp mắt của Quốc Việt.
- U20 Việt Nam 2-1 U20 Qatar: Quốc Việt và Văn Trường cùng nhau lập công, mở ra cơ hội vào tứ kết cho đội tuyển.
- U20 Việt Nam 1-3 U20 Iran: Một trận đấu đầy nỗ lực nhưng đáng tiếc đội tuyển không thể giành được tấm vé vào tứ kết.
Đánh Giá và Kỳ Vọng
Đội tuyển U20 Việt Nam đã có những màn trình diễn ấn tượng tại vòng bảng, dù không thể tiến vào tứ kết nhưng các cầu thủ trẻ đã cho thấy tiềm năng và sự phát triển mạnh mẽ. Người hâm mộ kỳ vọng rằng đội tuyển sẽ tiếp tục nỗ lực và đạt được những thành công lớn hơn trong tương lai.
Thống Kê Quan Trọng
- Số trận đã đấu: 3
- Số trận thắng: 2
- Số trận thua: 1
- Bàn thắng ghi được: 4
- Bàn thắng bị thủng lưới: 3
Đội tuyển U20 Việt Nam dù gặp phải những đối thủ mạnh nhưng đã thi đấu rất kiên cường. Hãy cùng tiếp tục ủng hộ các cầu thủ trẻ trên con đường phát triển sự nghiệp bóng đá.

.png)
Mục Lục Tổng Hợp Nội Dung
Dưới đây là mục lục tổng hợp các nội dung liên quan đến lịch thi đấu bóng đá Việt Nam U20, từ thông tin chi tiết về các trận đấu, đội hình, đối thủ đến các sự kiện và câu chuyện bên lề, giúp bạn không bỏ lỡ bất kỳ chi tiết nào trong hành trình của đội tuyển U20 Việt Nam.
- Lịch Thi Đấu Chi Tiết Của Đội Tuyển U20 Việt Nam
- Ngày, giờ và địa điểm các trận đấu
- Cách thức theo dõi và phát sóng trực tiếp
- Kết quả cập nhật từng trận đấu
- Phân Tích Sức Mạnh Của Đội Tuyển U20 Việt Nam
- Đánh giá đội hình và chiến thuật của U20 Việt Nam
- Các cầu thủ nổi bật và tiềm năng
- So sánh với các đối thủ cùng bảng
- Thông Tin Về Các Đối Thủ Của U20 Việt Nam
- Đội tuyển U20 Australia: Lịch sử và thành tích
- Đội tuyển U20 Qatar: Những điểm mạnh và yếu
- Đội tuyển U20 Iran: Phân tích chi tiết về lối chơi
- Những Câu Chuyện Bên Lề Giải Đấu
- Hành trình chuẩn bị của đội tuyển U20 Việt Nam
- Cảm xúc của người hâm mộ trước các trận đấu
- Những khoảnh khắc đáng nhớ của U20 Việt Nam
- Dự Đoán Và Nhận Định Kết Quả Giải Đấu
- Dự đoán kết quả các trận đấu tại bảng B
- Các yếu tố ảnh hưởng đến kết quả chung cuộc
- Nhận định cơ hội vào vòng trong của U20 Việt Nam
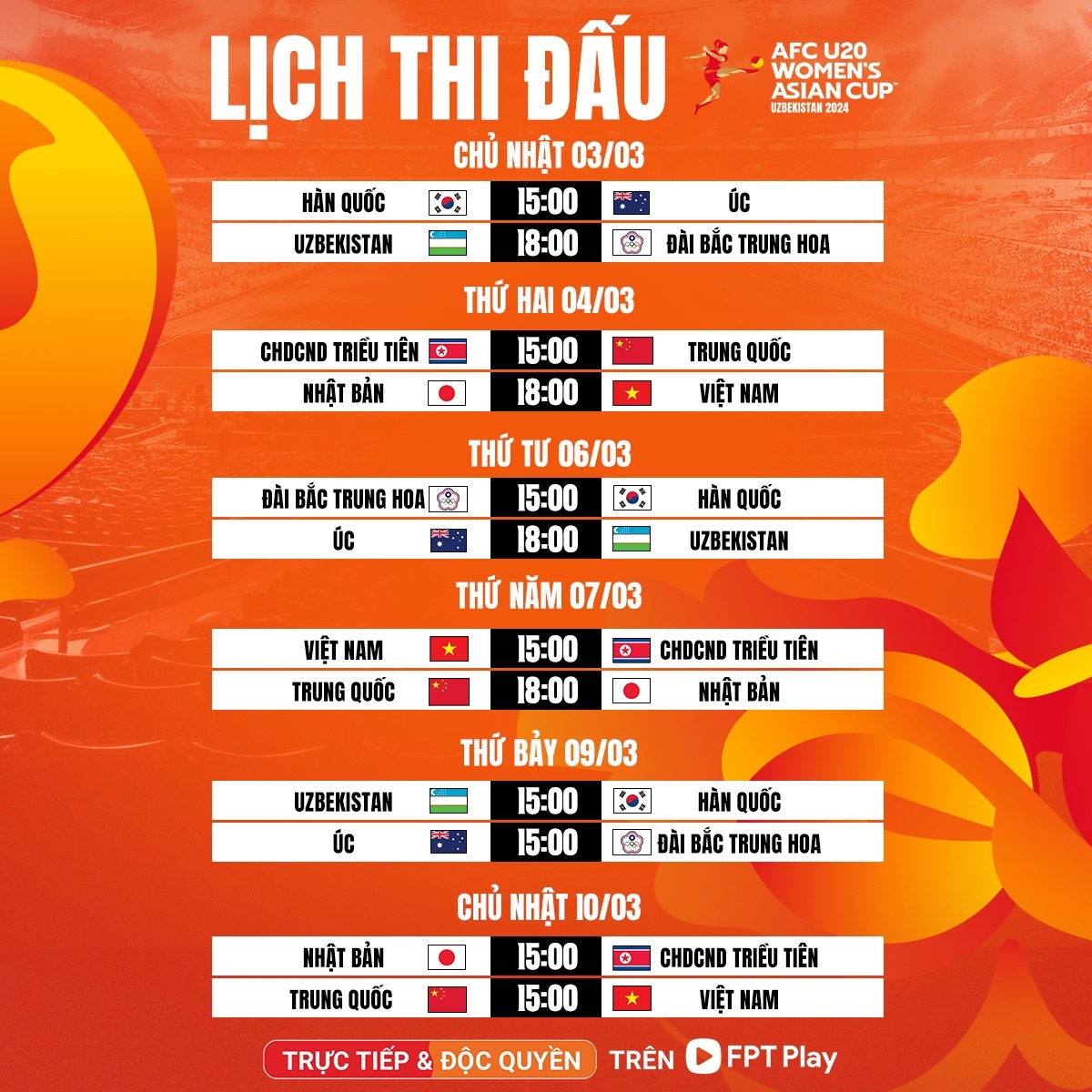
1. Lịch Thi Đấu Vòng Chung Kết U20 Châu Á 2023
Vòng chung kết U20 Châu Á 2023 là sự kiện quan trọng mà đội tuyển U20 Việt Nam sẽ tham gia với mục tiêu vượt qua vòng bảng và tiến sâu vào giải đấu. Dưới đây là lịch thi đấu chi tiết của đội tuyển Việt Nam tại bảng B:
- Ngày 1/3/2023: U20 Việt Nam vs U20 Australia - 17:00 (giờ Việt Nam) tại sân Istiqlol, Fergana.
- Ngày 4/3/2023: U20 Việt Nam vs U20 Qatar - 21:00 (giờ Việt Nam) tại sân Istiqlol, Fergana.
- Ngày 7/3/2023: U20 Việt Nam vs U20 Iran - 17:00 (giờ Việt Nam) tại sân Istiqlol, Fergana.
Tất cả các trận đấu đều diễn ra tại Uzbekistan. Đội tuyển U20 Việt Nam sẽ cần nỗ lực hết mình để vượt qua các đối thủ mạnh trong bảng B, bao gồm Australia, Qatar, và Iran. Đây là những trận đấu quyết định cho hy vọng tiến xa của U20 Việt Nam trong giải đấu năm nay.

2. Thông Tin Về Đội Tuyển U20 Việt Nam
Đội tuyển U20 Việt Nam là niềm hy vọng lớn của bóng đá Việt Nam tại giải U20 Châu Á 2023. Đội hình năm nay được đánh giá cao với nhiều cầu thủ trẻ tài năng và sự dẫn dắt đầy kinh nghiệm của HLV Hoàng Anh Tuấn. Dưới đây là những thông tin chi tiết về đội tuyển:
- Danh sách cầu thủ:
- Thủ môn: Văn Việt, Tuấn Hưng
- Hậu vệ: Đức Anh, Văn Cường, Văn Khang, Quốc Việt
- Tiền vệ: Văn Trường, Văn Tú, Thanh Nhàn
- Tiền đạo: Quốc Việt, Vỹ Hào, Đình Bắc
- Chiến thuật thi đấu: Đội tuyển U20 Việt Nam dưới sự chỉ đạo của HLV Hoàng Anh Tuấn sử dụng lối chơi linh hoạt, chú trọng phòng ngự chặt chẽ và tận dụng cơ hội phản công nhanh. Đội hình 4-3-3 được sử dụng để tối ưu hóa khả năng tấn công biên và tạo áp lực lên đối phương.
- Cầu thủ nổi bật: Quốc Việt là cái tên được kỳ vọng nhất trong đội hình năm nay. Với khả năng ghi bàn ấn tượng, anh là mũi nhọn tấn công chính của U20 Việt Nam. Bên cạnh đó, Văn Trường và Thanh Nhàn cũng là những cầu thủ trẻ tiềm năng có thể tạo đột biến.
- Mục tiêu và kỳ vọng: Đội tuyển U20 Việt Nam đặt mục tiêu lọt vào tứ kết và xa hơn là cạnh tranh một suất tham dự U20 World Cup 2023. Với sự chuẩn bị kỹ lưỡng và tinh thần thi đấu cao, đội tuyển hy vọng sẽ mang lại niềm tự hào cho người hâm mộ Việt Nam.

3. Đối Thủ Của U20 Việt Nam
Tại vòng chung kết U20 Châu Á 2023, U20 Việt Nam nằm ở bảng B cùng với các đối thủ mạnh gồm U20 Australia, U20 Qatar, và U20 Iran. Đây là những đội bóng có bề dày kinh nghiệm và thành tích đáng kể trong các giải đấu khu vực. Dưới đây là thông tin chi tiết về từng đối thủ:
- U20 Australia:
- Thành tích: U20 Australia là một trong những đội bóng hàng đầu châu Á với nhiều lần tham dự U20 World Cup. Đội bóng này nổi bật với lối chơi tốc độ và thể lực vượt trội.
- Cầu thủ đáng chú ý: Marco Tilio - tiền đạo có khả năng tạo đột biến cao, thường xuyên góp mặt trong đội hình chính của U20 Australia.
- Chiến thuật: U20 Australia thường áp dụng lối chơi pressing mạnh mẽ, kết hợp với các đường chuyền dài để tận dụng tốc độ của các cầu thủ tấn công.
- U20 Qatar:
- Thành tích: U20 Qatar đã từng vô địch U20 Châu Á và có chương trình đào tạo trẻ rất tốt, được đầu tư kỹ lưỡng với mục tiêu phát triển bóng đá lâu dài.
- Cầu thủ đáng chú ý: Hashim Ali - một tiền vệ trung tâm đầy tài năng, có khả năng kiểm soát trận đấu và phát động tấn công từ xa.
- Chiến thuật: Đội bóng này sử dụng lối chơi kiểm soát bóng, xây dựng các đợt tấn công từ trung tuyến và khai thác khoảng trống phía sau hàng phòng ngự đối phương.
- U20 Iran:
- Thành tích: U20 Iran là một trong những đội bóng mạnh nhất khu vực Tây Á, luôn được biết đến với lối chơi quyết liệt và kỷ luật.
- Cầu thủ đáng chú ý: Mehdi Ghayedi - tiền đạo nhỏ con nhưng nhanh nhẹn, có kỹ thuật cá nhân xuất sắc và khả năng dứt điểm đa dạng.
- Chiến thuật: U20 Iran thường sử dụng đội hình phòng ngự phản công, với hàng thủ chặt chẽ và những đường phản công sắc bén.
Các đối thủ của U20 Việt Nam tại bảng B đều là những đội bóng mạnh và có lối chơi riêng biệt. Để vượt qua vòng bảng, U20 Việt Nam cần phải nắm rõ điểm mạnh và điểm yếu của từng đối thủ, từ đó đưa ra chiến thuật hợp lý trong mỗi trận đấu.

4. Các Trận Đấu Giao Hữu Trước Giải
Trước khi bước vào vòng chung kết U20 Châu Á 2023, đội tuyển U20 Việt Nam đã có một loạt các trận đấu giao hữu để chuẩn bị tốt nhất về mặt chiến thuật cũng như tinh thần thi đấu. Những trận giao hữu này giúp HLV Hoàng Anh Tuấn thử nghiệm đội hình và điều chỉnh các chiến thuật phù hợp. Dưới đây là thông tin chi tiết về các trận đấu giao hữu của đội tuyển:
- Trận đấu với U20 Ả Rập Xê Út:
- Thời gian: Ngày 15/02/2023
- Kết quả: U20 Việt Nam thua 0-2
- Nhận xét: Trận đấu này là một thử thách lớn đối với U20 Việt Nam khi đối đầu với đội bóng mạnh đến từ Tây Á. Mặc dù thua trận, nhưng đội tuyển đã rút ra nhiều bài học quý giá về khả năng phòng ngự và phản công.
- Trận đấu với U20 UAE:
- Thời gian: Ngày 20/02/2023
- Kết quả: Hòa 1-1
- Nhận xét: Đây là một trận đấu cân bằng, khi cả hai đội đều có những cơ hội riêng. U20 Việt Nam đã thể hiện tinh thần chiến đấu mạnh mẽ và sự gắn kết trong lối chơi.
- Trận đấu với U20 Oman:
- Thời gian: Ngày 25/02/2023
- Kết quả: Thắng 2-0
- Nhận xét: Chiến thắng này giúp đội tuyển U20 Việt Nam củng cố tinh thần và tự tin trước khi bước vào giải đấu chính thức. Các cầu thủ đã thể hiện sự tiến bộ rõ rệt trong việc tổ chức tấn công và kiểm soát trận đấu.
Các trận đấu giao hữu đã đóng vai trò quan trọng trong việc hoàn thiện chiến thuật của đội tuyển U20 Việt Nam. Qua từng trận đấu, HLV Hoàng Anh Tuấn đã tìm ra những điểm mạnh, điểm yếu và đưa ra các điều chỉnh kịp thời để chuẩn bị tốt nhất cho vòng chung kết U20 Châu Á 2023.
XEM THÊM:
5. Thông Tin Bên Lề Giải Đấu
Giải U20 Châu Á 2023 đã mang đến nhiều câu chuyện thú vị và sự quan tâm lớn từ người hâm mộ cũng như truyền thông. Dưới đây là một số thông tin bên lề nổi bật:
5.1. Sự Quan Tâm Của Người Hâm Mộ Và Truyền Thông
- Đội tuyển U20 Việt Nam nhận được sự cổ vũ mạnh mẽ từ khán giả nhà dù giải đấu diễn ra ở Uzbekistan. Các buổi tập luyện và trận giao hữu của đội luôn được cập nhật liên tục trên các phương tiện truyền thông, với hàng loạt bài viết, hình ảnh và video phỏng vấn cầu thủ.
- Các cổ động viên đã tổ chức nhiều hoạt động sôi nổi như thiết kế băng rôn, cờ và thậm chí là các buổi giao lưu trực tuyến để cổ vũ cho đội tuyển trước các trận đấu quan trọng. Sự kỳ vọng và niềm tin vào khả năng tiến xa của đội đã thúc đẩy một không khí rất tích cực xung quanh giải đấu.
5.2. Những Câu Chuyện Thú Vị Bên Lề Giải Đấu
- Trong quá trình chuẩn bị cho giải, đội tuyển U20 Việt Nam đã có chuyến tập huấn tại UAE và có các trận giao hữu với các đối thủ mạnh như Saudi Arabia và Dubai FC. Điều này không chỉ giúp các cầu thủ rèn luyện khả năng thi đấu quốc tế mà còn mang đến nhiều kinh nghiệm quý báu trước khi bước vào giải chính thức.
- Đặc biệt, chiến thắng trước đội U20 Saudi Arabia với tỷ số 2-1 trong trận giao hữu đã tạo nên cú hích lớn về tinh thần cho toàn đội. Đây là một tín hiệu tích cực cho thấy U20 Việt Nam đã sẵn sàng đối mặt với những thách thức tại bảng "tử thần" của giải đấu.
- Trong khi đó, một số cầu thủ phải hội quân muộn do lịch thi đấu của V-League, điều này đã gây ra những khó khăn nhất định trong việc tập luyện chung của đội. Tuy nhiên, ban huấn luyện đã khéo léo điều chỉnh và duy trì sự ổn định cho toàn đội.
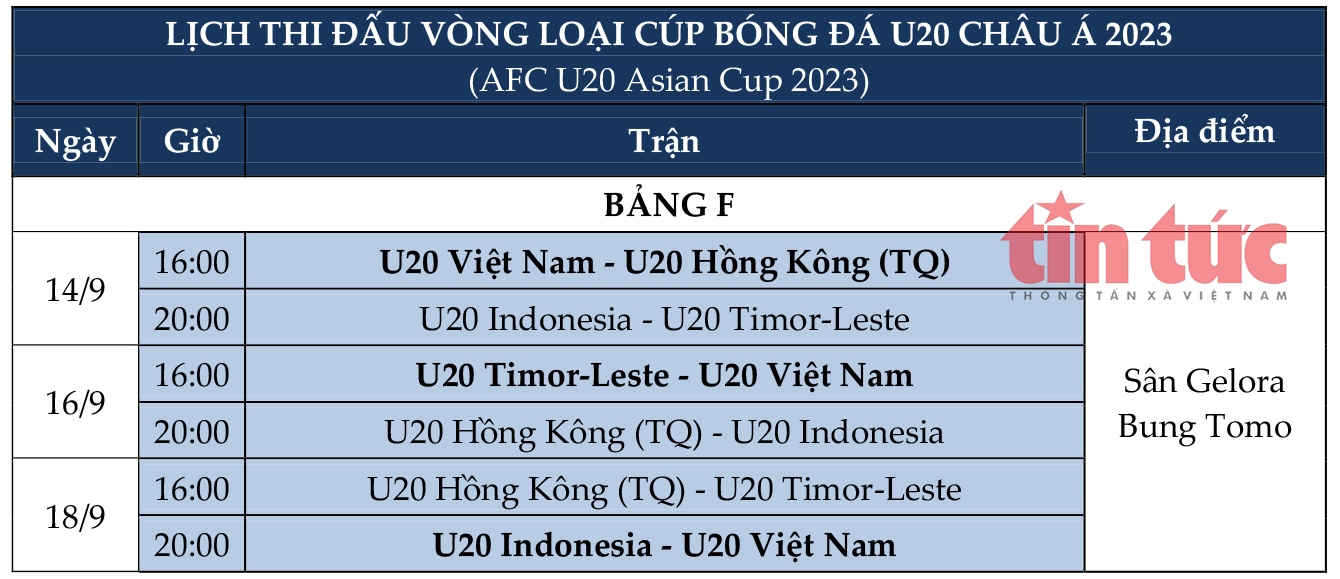
6. Phân Tích Và Dự Đoán Kết Quả Giải Đấu
Vòng chung kết U20 châu Á 2023 hứa hẹn là một cuộc cạnh tranh đầy kịch tính với sự góp mặt của những đội bóng mạnh nhất khu vực. Đội tuyển U20 Việt Nam nằm trong bảng B, nơi quy tụ các đối thủ nặng ký như U20 Iran, U20 Australia và U20 Qatar. Đây đều là những đội tuyển có bề dày thành tích và kinh nghiệm thi đấu quốc tế.
6.1. Dự đoán kết quả bảng B
- U20 Việt Nam vs U20 Australia (1/3/2023): Trận ra quân luôn là thử thách lớn cho U20 Việt Nam khi đối đầu với một Australia sở hữu lối chơi mạnh mẽ và kỷ luật. Tuy nhiên, với sự chuẩn bị kỹ lưỡng và tinh thần chiến đấu cao, U20 Việt Nam hoàn toàn có thể hy vọng vào một kết quả hòa hoặc thậm chí là chiến thắng nếu tận dụng tốt cơ hội.
- U20 Việt Nam vs U20 Qatar (4/3/2023): Đây là trận đấu then chốt quyết định lớn đến cơ hội đi tiếp của Việt Nam. Qatar với lối đá tấn công sắc bén sẽ là thử thách không nhỏ, nhưng nếu duy trì được sự chắc chắn trong phòng ngự và phản công nhanh, U20 Việt Nam có thể giành điểm trước đối thủ này.
- U20 Việt Nam vs U20 Iran (7/3/2023): Trận đấu cuối cùng vòng bảng sẽ đối đầu với một U20 Iran luôn được đánh giá cao tại các giải đấu trẻ. Đây là trận đấu mà U20 Việt Nam cần phải có ít nhất 1 điểm để nuôi hy vọng vào tứ kết. Tuy nhiên, một chiến thắng sẽ là động lực tinh thần cực lớn cho các cầu thủ trẻ Việt Nam.
6.2. Phân tích cơ hội tiến xa của U20 Việt Nam
U20 Việt Nam đã thể hiện sự tiến bộ qua từng giải đấu quốc tế gần đây. Dưới sự dẫn dắt của HLV Hoàng Anh Tuấn, đội bóng không chỉ mạnh mẽ về thể lực mà còn có sự gắn kết trong lối chơi. Mặc dù phải đối mặt với những đối thủ mạnh ở vòng bảng, nhưng nếu các cầu thủ giữ vững tinh thần thi đấu và tận dụng tốt cơ hội, U20 Việt Nam hoàn toàn có khả năng tiến sâu vào vòng sau, thậm chí là cạnh tranh suất dự World Cup U20.
6.3. Các yếu tố có thể ảnh hưởng đến kết quả trận đấu
Yếu tố thời tiết, điều kiện sân bãi tại Uzbekistan và áp lực từ các trận đấu có thể ảnh hưởng đến phong độ của U20 Việt Nam. Bên cạnh đó, kinh nghiệm thi đấu quốc tế của các cầu thủ cũng là một yếu tố quan trọng. Tuy nhiên, với sự chuẩn bị kỹ lưỡng và chiến thuật hợp lý, U20 Việt Nam có thể vượt qua các thách thức này để tạo nên bất ngờ tại giải đấu năm nay.

7. Lời Khuyên Cho Người Hâm Mộ
Để ủng hộ đội tuyển U20 Việt Nam tại giải đấu, người hâm mộ cần chuẩn bị kỹ lưỡng cả về tâm lý và tinh thần. Dưới đây là một số lời khuyên hữu ích:
7.1. Cách theo dõi trực tiếp các trận đấu
- Lựa chọn kênh phát sóng: Đảm bảo bạn đã xác định được kênh truyền hình hoặc nền tảng trực tuyến phát sóng trực tiếp các trận đấu của U20 Việt Nam. Các trận đấu thường được phát trên VTV6 hoặc các kênh thể thao lớn.
- Cập nhật lịch thi đấu: Lịch thi đấu của U20 Việt Nam có thể thay đổi, do đó, hãy thường xuyên cập nhật thông tin từ các nguồn chính thức như trang web của liên đoàn bóng đá hoặc các kênh truyền thông uy tín.
- Tạo không khí cổ vũ: Nếu không thể đến sân, hãy tạo không gian cổ vũ tại nhà cùng bạn bè và gia đình. Sử dụng cờ, băng rôn, và áo đấu để tạo không khí sôi động.
7.2. Gợi ý tham gia các hoạt động cổ vũ tại nhà
- Tổ chức buổi xem chung: Mời bạn bè đến nhà cùng xem trận đấu. Hãy chuẩn bị một số món ăn nhẹ và đồ uống để buổi cổ vũ thêm phần thú vị.
- Tương tác trực tuyến: Tham gia các nhóm cổ động viên trên mạng xã hội để chia sẻ cảm xúc và cập nhật thông tin về trận đấu. Điều này không chỉ giúp bạn có thêm thông tin mà còn tăng cường tinh thần đoàn kết.
- Thể hiện sự ủng hộ: Đăng tải những thông điệp cổ vũ trên mạng xã hội kèm theo hashtag liên quan đến đội tuyển U20 Việt Nam. Điều này sẽ lan tỏa tình yêu bóng đá và động viên tinh thần cho các cầu thủ.
Cuối cùng, hãy luôn giữ vững niềm tin và ủng hộ hết mình, bất kể kết quả ra sao. Đội tuyển U20 Việt Nam đang trên con đường phát triển và rất cần sự ủng hộ từ người hâm mộ để có thể đạt được những thành công trong tương lai.
10 Dạng Bài Tập Toán Học Có Lời Giải
Toán học là môn học đòi hỏi sự tư duy và khả năng phân tích cao. Dưới đây là 10 dạng bài tập toán học phổ biến cùng với lời giải chi tiết, giúp các bạn học sinh có thể nắm vững kiến thức và áp dụng trong các kỳ thi.
Dạng 1: Phương Trình Bậc Hai Một Ẩn
Phương trình bậc hai là nền tảng quan trọng trong toán học. Dạng bài này yêu cầu giải phương trình dạng \[ax^2 + bx + c = 0\] và tìm các nghiệm của phương trình.
- Đưa phương trình về dạng chuẩn.
- Sử dụng công thức nghiệm: \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
- Kiểm tra và kết luận các nghiệm của phương trình.
Dạng 2: Hệ Phương Trình Tuyến Tính
Hệ phương trình tuyến tính thường xuất hiện trong các bài toán liên quan đến nhiều ẩn. Để giải hệ phương trình dạng này:
- Đưa hệ phương trình về dạng ma trận nếu có thể.
- Sử dụng phương pháp thế hoặc phương pháp cộng đại số để tìm nghiệm.
- Đối với hệ phương trình có nhiều ẩn, sử dụng phương pháp Gauss để giải.
Dạng 3: Giải Bất Đẳng Thức
Giải bất đẳng thức đòi hỏi học sinh phải nắm vững kiến thức về định lý và các tính chất của bất đẳng thức. Ví dụ, với bất đẳng thức dạng:
Học sinh cần giải tìm miền nghiệm và biểu diễn trên trục số.
Dạng 4: Tính Toán Với Số Phức
Số phức là một phần quan trọng trong toán học nâng cao. Bài tập dạng này thường yêu cầu học sinh thực hiện các phép tính như cộng, trừ, nhân, chia số phức và tìm mô-đun của số phức.
Dạng 5: Phương Trình Lượng Giác
Phương trình lượng giác bao gồm các hàm số như sin, cos, tan,... Để giải dạng bài này, cần nắm vững các công thức lượng giác cơ bản và sử dụng các phép biến đổi phù hợp.
Dạng 6: Đạo Hàm và Ứng Dụng
Đạo hàm là công cụ mạnh mẽ trong việc nghiên cứu sự biến thiên của hàm số. Bài tập dạng này thường yêu cầu tìm đạo hàm của hàm số và áp dụng vào bài toán cực trị, tính đơn điệu của hàm số.
Dạng 7: Tích Phân Cơ Bản
Tích phân được dùng để tính diện tích dưới đồ thị của một hàm số. Dạng bài này thường yêu cầu tính tích phân của các hàm số đơn giản và áp dụng vào các bài toán vật lý.
Dạng 8: Ứng Dụng Của Hình Học Giải Tích
Hình học giải tích kết hợp giữa hình học và đại số để giải quyết các bài toán liên quan đến đường thẳng, mặt phẳng và đường cong trong không gian.
Dạng 9: Bài Toán Tổ Hợp
Tổ hợp là một lĩnh vực của toán học liên quan đến việc đếm các đối tượng. Bài tập dạng này yêu cầu tính toán số cách chọn, sắp xếp đối tượng theo các quy tắc nhất định.
Dạng 10: Xác Suất Thống Kê
Xác suất thống kê được sử dụng để dự đoán khả năng xảy ra của một sự kiện. Dạng bài này bao gồm tính xác suất của các biến cố đơn giản và phức tạp, cũng như phân tích dữ liệu thống kê.

Dạng 1: Phương Trình Bậc Hai Một Ẩn
Phương trình bậc hai một ẩn là một trong những dạng bài tập cơ bản và quan trọng trong toán học, thường được biểu diễn dưới dạng tổng quát:
Trong đó:
- \(a\), \(b\), \(c\) là các hệ số, với \(a \neq 0\).
- \(x\) là ẩn số cần tìm.
1.1. Công thức nghiệm của phương trình bậc hai
Để giải phương trình bậc hai, ta sử dụng công thức nghiệm:
Trong đó:
- \(\Delta = b^2 - 4ac\) gọi là biệt thức (hay discriminant).
- Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\), phương trình có nghiệm kép (hay nghiệm trùng).
- Nếu \(\Delta < 0\), phương trình vô nghiệm trên tập số thực.
1.2. Ví dụ minh họa
Xét phương trình bậc hai sau:
Ta tính biệt thức \(\Delta\):
Vì \(\Delta = 0\), nên phương trình có nghiệm kép:
Vậy nghiệm của phương trình là \(x = 1\).
1.3. Ứng dụng của phương trình bậc hai
Phương trình bậc hai xuất hiện nhiều trong các bài toán thực tế như tính toán đường đi, tối ưu hóa chi phí, và trong vật lý khi xét các chuyển động. Hiểu và giải thành thạo phương trình bậc hai sẽ giúp học sinh nắm vững nền tảng toán học và áp dụng vào nhiều lĩnh vực khác nhau.
Dạng 2: Hệ Phương Trình Tuyến Tính
Hệ phương trình tuyến tính là một trong những dạng toán cơ bản và quan trọng trong đại số, được sử dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Một hệ phương trình tuyến tính có thể được biểu diễn dưới dạng:
Trong đó:
- \(a_1\), \(b_1\), \(c_1\) và \(a_2\), \(b_2\), \(c_2\) là các hệ số của phương trình.
- \(x\) và \(y\) là các biến số cần tìm.
2.1. Phương pháp giải hệ phương trình tuyến tính
Có nhiều phương pháp để giải hệ phương trình tuyến tính, dưới đây là ba phương pháp phổ biến:
- Phương pháp thế: Từ một phương trình trong hệ, giải \(x\) hoặc \(y\) theo biểu thức của phương trình còn lại, sau đó thay vào phương trình kia.
- Phương pháp cộng đại số: Nhân một hoặc cả hai phương trình với các hệ số thích hợp để tạo ra hệ số của một trong các biến bằng nhau, sau đó trừ hoặc cộng hai phương trình để loại bỏ biến đó.
- Phương pháp ma trận: Viết hệ phương trình dưới dạng ma trận, rồi sử dụng các phép biến đổi hàng cơ bản để tìm nghiệm của hệ.
2.2. Ví dụ minh họa
Giải hệ phương trình sau:
Phương pháp thế:
- Giải phương trình thứ hai theo \(y\): \(y = 4x - 5\).
- Thay giá trị của \(y\) vào phương trình đầu: \(2x + 3(4x - 5) = 6\).
- Giải phương trình để tìm \(x\): \(2x + 12x - 15 = 6\), suy ra \(x = \frac{21}{14}\).
- Thay \(x\) vào phương trình \(y = 4x - 5\) để tìm \(y\).
Kết quả, nghiệm của hệ là:
2.3. Ứng dụng của hệ phương trình tuyến tính
Hệ phương trình tuyến tính có nhiều ứng dụng trong thực tế như tính toán mạng điện, tối ưu hóa sản xuất, và phân tích số liệu trong kinh tế học. Việc thành thạo các phương pháp giải hệ phương trình tuyến tính là rất quan trọng để giải quyết các bài toán phức tạp trong các ngành khoa học và kỹ thuật.
Dạng 3: Giải Bất Đẳng Thức
Bất đẳng thức là một trong những chủ đề quan trọng trong toán học, thường được sử dụng để so sánh các giá trị và xác định các miền giá trị của biến số. Một bất đẳng thức có dạng tổng quát:
Trong đó \(f(x)\) và \(g(x)\) là các hàm số hoặc biểu thức đại số. Mục tiêu là tìm tập nghiệm \(x\) thỏa mãn bất đẳng thức này.
3.1. Phương pháp giải bất đẳng thức
Có nhiều phương pháp khác nhau để giải bất đẳng thức, trong đó phổ biến nhất là:
- Phương pháp biến đổi tương đương: Sử dụng các phép biến đổi đại số để đơn giản hóa bất đẳng thức và tìm ra miền giá trị của biến số.
- Phương pháp xét dấu tam thức bậc hai: Đối với các bất đẳng thức dạng tam thức bậc hai, sử dụng phương pháp xét dấu của biểu thức để xác định miền giá trị của biến số.
- Phương pháp đồ thị: Dùng đồ thị của các hàm số để trực quan hóa miền nghiệm của bất đẳng thức.
3.2. Ví dụ minh họa
Xét bất đẳng thức sau:
Để giải, ta tiến hành phân tích biểu thức thành nhân tử:
Bất đẳng thức trở thành:
Sử dụng phương pháp xét dấu, ta có nghiệm:
- \(x < 1\)
- \(x > 3\)
Vậy miền nghiệm của bất đẳng thức là:
3.3. Ứng dụng của bất đẳng thức
Bất đẳng thức có nhiều ứng dụng trong toán học và đời sống thực tiễn như tối ưu hóa, phân tích và dự đoán các kết quả. Nó cũng là nền tảng để hiểu sâu hơn về các hàm số và các hiện tượng tự nhiên.
Dạng 4: Tính Toán Với Số Phức
Số phức là một khái niệm mở rộng của số thực, bao gồm cả phần thực và phần ảo. Một số phức thường được biểu diễn dưới dạng:
Trong đó:
- \(a\) là phần thực của số phức \(z\).
- \(b\) là phần ảo của số phức \(z\).
- \(i\) là đơn vị ảo, với tính chất \(i^2 = -1\).
4.1. Các phép toán cơ bản với số phức
Các phép toán cơ bản với số phức bao gồm:
- Phép cộng: Để cộng hai số phức, ta cộng các phần thực với nhau và các phần ảo với nhau: \[ (a + bi) + (c + di) = (a + c) + (b + d)i \]
- Phép trừ: Tương tự như phép cộng, nhưng trừ từng phần: \[ (a + bi) - (c + di) = (a - c) + (b - d)i \]
- Phép nhân: Khi nhân hai số phức, ta phân phối và sử dụng tính chất \(i^2 = -1\): \[ (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i \]
- Phép chia: Để chia hai số phức, ta nhân cả tử và mẫu với liên hợp của mẫu: \[ \frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \]
4.2. Mô-đun và liên hợp của số phức
Mô-đun của một số phức \(z = a + bi\) là khoảng cách từ \(z\) đến gốc tọa độ trong mặt phẳng phức, được tính bằng công thức:
Liên hợp của số phức \(z = a + bi\) là số phức \(z^* = a - bi\). Liên hợp được sử dụng trong nhiều phép tính, đặc biệt là khi chia số phức.
4.3. Ví dụ minh họa
Xét hai số phức \(z_1 = 2 + 3i\) và \(z_2 = 1 - 4i\). Chúng ta thực hiện các phép toán sau:
- Phép cộng: \[ z_1 + z_2 = (2 + 1) + (3 - 4)i = 3 - i \]
- Phép nhân: \[ z_1 \cdot z_2 = (2 \times 1 - 3 \times -4) + (2 \times -4 + 3 \times 1)i = 14 - 5i \]
- Phép chia: \[ \frac{z_1}{z_2} = \frac{(2 + 3i)(1 + 4i)}{1^2 + (-4)^2} = \frac{2 + 8i + 3i - 12}{17} = \frac{-10 + 11i}{17} \]
4.4. Ứng dụng của số phức
Số phức có ứng dụng rộng rãi trong nhiều lĩnh vực như kỹ thuật điện, cơ học lượng tử, lý thuyết điều khiển, và trong việc giải các phương trình đại số bậc hai có nghiệm phức.
Dạng 5: Phương Trình Lượng Giác
Phương trình lượng giác là một loại phương trình trong toán học mà các ẩn số xuất hiện trong các hàm lượng giác như sin, cos, tan, và cot. Việc giải các phương trình này yêu cầu phải nắm vững các công thức lượng giác cơ bản và các phương pháp biến đổi tương đương. Dưới đây là một số phương pháp và ví dụ cụ thể để giải phương trình lượng giác.
5.1. Phương pháp giải cơ bản
Các phương pháp thường dùng để giải phương trình lượng giác bao gồm:
- Biến đổi lượng giác: Sử dụng các công thức lượng giác để biến đổi phương trình về dạng đơn giản hơn.
- Phân tích nhân tử: Tách phương trình thành các nhân tử rồi giải từng phương trình con.
- Đặt ẩn phụ: Đôi khi cần đặt ẩn phụ để đưa phương trình về dạng dễ giải hơn.
- Sử dụng bảng giá trị: Đối với các giá trị đặc biệt của các hàm lượng giác, có thể sử dụng bảng giá trị để tìm nghiệm.
5.2. Ví dụ cụ thể
Xét ví dụ sau:
Để giải phương trình này, ta có thể thực hiện các bước sau:
- Áp dụng công thức biến đổi: Sử dụng công thức \( \sin 2x = 2\sin x \cos x \), ta có: \[ 2\sin x \cos x - \sin x = 0 \]
- Phân tích nhân tử: \[ \sin x (2\cos x - 1) = 0 \]
- Giải từng phương trình con:
- Với \( \sin x = 0 \), ta có nghiệm \( x = k\pi \), với \( k \in \mathbb{Z} \).
- Với \( 2\cos x - 1 = 0 \), ta có nghiệm \( \cos x = \frac{1}{2} \), từ đó suy ra: \[ x = \pm \frac{\pi}{3} + 2k\pi, \text{ với } k \in \mathbb{Z}. \]
Vậy nghiệm của phương trình là:
5.3. Ứng dụng thực tiễn
Phương trình lượng giác có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc tính toán các dao động, phân tích sóng âm, và các bài toán về chuyển động tròn đều.
Dạng 6: Đạo Hàm và Ứng Dụng
Đạo hàm là một trong những khái niệm cơ bản và quan trọng nhất của giải tích. Đạo hàm của một hàm số tại một điểm đo lường sự thay đổi tức thời của hàm số tại điểm đó. Đạo hàm không chỉ được sử dụng để giải quyết các bài toán lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống, khoa học, và kỹ thuật.
6.1. Khái niệm đạo hàm
Cho hàm số \( y = f(x) \), đạo hàm của hàm số tại điểm \( x = a \) được định nghĩa là:
Nếu giới hạn trên tồn tại, ta nói hàm số \( f(x) \) có đạo hàm tại điểm \( x = a \). Đạo hàm này biểu diễn độ dốc của tiếp tuyến với đồ thị của hàm số tại điểm đó.
6.2. Các quy tắc tính đạo hàm cơ bản
Dưới đây là một số quy tắc tính đạo hàm thường gặp:
- Quy tắc tổng: \((f(x) + g(x))' = f'(x) + g'(x)\)
- Quy tắc nhân: \((f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\)
- Quy tắc chia: \(\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{g(x)^2}\)
- Quy tắc hàm hợp: Nếu \(y = f(g(x))\), thì \(y' = f'(g(x)) \cdot g'(x)\)
6.3. Ứng dụng của đạo hàm
Đạo hàm có nhiều ứng dụng quan trọng, dưới đây là một số ứng dụng tiêu biểu:
6.3.1. Tìm cực trị của hàm số
Đạo hàm giúp xác định các điểm cực trị (cực đại, cực tiểu) của hàm số. Để tìm các điểm này, ta cần giải phương trình:
Sau đó, ta xét dấu của \(f'(x)\) để xác định tính chất của các điểm này.
6.3.2. Ứng dụng trong kinh tế
Trong kinh tế, đạo hàm được sử dụng để tìm điểm tối ưu, chẳng hạn như điểm mà lợi nhuận đạt cực đại hoặc chi phí đạt cực tiểu. Ví dụ, nếu hàm số biểu diễn lợi nhuận là \(P(x)\), ta có thể tìm giá trị \(x\) sao cho \(P'(x) = 0\) để xác định mức sản xuất tối ưu.
6.3.3. Ứng dụng trong vật lý
Trong vật lý, đạo hàm được sử dụng để mô tả tốc độ thay đổi của các đại lượng vật lý. Ví dụ, nếu vị trí của một vật chuyển động theo thời gian được biểu diễn bởi hàm \(s(t)\), thì vận tốc tức thời của vật tại thời điểm \(t\) là đạo hàm của \(s(t)\):
Hơn nữa, gia tốc của vật cũng là đạo hàm của vận tốc theo thời gian:
6.3.4. Ứng dụng trong sinh học
Trong sinh học, đạo hàm được sử dụng để mô tả tốc độ tăng trưởng của quần thể hoặc tốc độ phản ứng sinh học. Ví dụ, nếu số lượng quần thể tại thời điểm \(t\) được biểu diễn bởi hàm \(N(t)\), thì tốc độ tăng trưởng tại thời điểm đó là:
6.4. Một số bài tập thực hành
Dưới đây là một số bài tập giúp củng cố kiến thức về đạo hàm và ứng dụng:
- Tính đạo hàm của các hàm số sau:
- \(f(x) = 3x^2 + 5x - 7\)
- \(g(x) = \frac{2x^3 - 3x + 4}{x^2}\)
- Tìm các điểm cực trị của hàm số \(h(x) = x^4 - 4x^3 + 6x^2 - 4x + 1\).
- Cho hàm số vị trí \(s(t) = t^3 - 6t^2 + 9t + 2\). Tìm vận tốc và gia tốc của vật tại thời điểm \(t = 2\).
Hãy làm các bài tập trên và so sánh kết quả với đáp án để tự đánh giá khả năng của bạn!
Dạng 7: Tích Phân Cơ Bản
Tích phân là một khái niệm quan trọng trong giải tích, giúp chúng ta tìm ra diện tích dưới đường cong, thể tích của một vật thể, và nhiều ứng dụng khác trong toán học cũng như thực tiễn. Bài viết này sẽ giới thiệu về cách tính tích phân cơ bản và các ứng dụng của nó.
1. Định nghĩa và tính chất cơ bản
Tích phân của một hàm số \( f(x) \) trên đoạn \([a, b]\) được định nghĩa là:
\[
\int_a^b f(x) \, dx
\]
Trong đó, \( a \) và \( b \) là các giới hạn tích phân, \( dx \) biểu thị biến vi phân.
Một số tính chất cơ bản của tích phân bao gồm:
- Tính tuyến tính: Nếu \( c \) là một hằng số và \( f(x), g(x) \) là hai hàm số, thì: \[ \int_a^b [c \cdot f(x) + g(x)] \, dx = c \cdot \int_a^b f(x) \, dx + \int_a^b g(x) \, dx \]
- Đảo giới hạn tích phân: \[ \int_a^b f(x) \, dx = -\int_b^a f(x) \, dx \]
- Tính chia đoạn: Nếu \( c \) nằm giữa \( a \) và \( b \), thì: \[ \int_a^b f(x) \, dx = \int_a^c f(x) \, dx + \int_c^b f(x) \, dx \]
2. Phương pháp tính tích phân cơ bản
Có nhiều phương pháp tính tích phân, trong đó phương pháp nguyên hàm và phương pháp biến đổi là hai phương pháp chính:
- Phương pháp nguyên hàm: Để tính tích phân \( \int f(x) \, dx \), ta cần tìm hàm số \( F(x) \) sao cho \( F'(x) = f(x) \). Khi đó: \[ \int_a^b f(x) \, dx = F(b) - F(a) \]
- Phương pháp biến đổi: Sử dụng các phép biến đổi như đổi biến số hoặc phân tích thành các tích phân đơn giản hơn để tính tích phân.
3. Ứng dụng của tích phân cơ bản
Tích phân cơ bản có nhiều ứng dụng thực tế:
- Tính diện tích dưới đường cong: Diện tích dưới đường cong \( y = f(x) \) từ \( x = a \) đến \( x = b \) được tính bằng tích phân: \[ \text{Diện tích} = \int_a^b f(x) \, dx \]
- Tính thể tích của vật thể: Thể tích của vật thể quay quanh trục \( x \) có thể được tính bằng tích phân của diện tích mặt cắt ngang.
- Ứng dụng trong vật lý: Tích phân được sử dụng để tính các đại lượng như công, năng lượng, và điện tích trong các bài toán vật lý.
4. Bài tập ví dụ
Dưới đây là một ví dụ minh họa cho việc tính tích phân:
Tính tích phân:
\[
\int_0^1 (3x^2 + 2x + 1) \, dx
\]
Giải:
\[
\int_0^1 (3x^2 + 2x + 1) \, dx = \left[ x^3 + x^2 + x \right]_0^1 = 1 + 1 + 1 - (0 + 0 + 0) = 3
\]
Dạng 8: Ứng Dụng Của Hình Học Giải Tích
Hình học giải tích là một phần quan trọng trong toán học, giúp giải quyết các bài toán liên quan đến không gian và các đối tượng hình học bằng cách sử dụng các phương trình và bất phương trình. Dưới đây là một số ứng dụng cụ thể của hình học giải tích mà chúng ta có thể áp dụng trong các bài toán thực tế.
1. Tìm Phương Trình Đường Thẳng
Trong mặt phẳng tọa độ, một đường thẳng có thể được xác định bởi một điểm và một vector chỉ phương, hoặc bởi hai điểm phân biệt. Phương trình đường thẳng có dạng tổng quát là:
\[ ax + by + c = 0 \]
Trong đó, \((a, b)\) là vector pháp tuyến của đường thẳng. Một ứng dụng phổ biến của phương trình đường thẳng là xác định khoảng cách từ một điểm đến đường thẳng.
2. Xác Định Tâm và Bán Kính Đường Tròn
Đường tròn là tập hợp các điểm trong mặt phẳng cách đều một điểm cố định gọi là tâm. Phương trình đường tròn có dạng:
\[ (x - a)^2 + (y - b)^2 = r^2 \]
Trong đó, \((a, b)\) là tọa độ tâm và \(r\) là bán kính. Ứng dụng này rất hữu ích trong các bài toán liên quan đến quỹ đạo của các vật thể chuyển động trong không gian.
3. Phương Trình Đường Elip và Ứng Dụng
Đường elip là một đường cong đóng, mô tả quỹ đạo của các hành tinh quay quanh Mặt Trời theo định luật Kepler. Phương trình đường elip có dạng:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Trong đó, \(a\) và \(b\) là các bán trục lớn và nhỏ của elip. Hình học giải tích giúp chúng ta xác định các điểm đặc biệt trên elip, như tiêu điểm và đỉnh, cùng với các ứng dụng trong thiên văn học và cơ học.
4. Ứng Dụng Trong Tìm Giao Điểm Của Các Đường
Việc tìm giao điểm của hai hay nhiều đường thẳng, đường tròn hoặc đường cong là một ứng dụng quan trọng của hình học giải tích. Giao điểm chính là nghiệm chung của các phương trình mô tả các đường này.
Ví dụ, giao điểm của hai đường thẳng được tìm bằng cách giải hệ phương trình:
\[
\begin{cases}
ax + by + c = 0 \\
dx + ey + f = 0
\end{cases}
\]
5. Tính Diện Tích và Thể Tích Sử Dụng Tích Phân
Hình học giải tích kết hợp với phép tính tích phân để tính toán diện tích của các hình phẳng và thể tích của các khối đa diện. Ví dụ, diện tích của một miền phẳng giới hạn bởi đường cong có thể được tính bằng tích phân:
\[
S = \int_{a}^{b} f(x) \, dx
\]
Trong đó, \(f(x)\) là hàm số mô tả biên của miền cần tính diện tích.
Ứng dụng của hình học giải tích rất rộng rãi trong nhiều lĩnh vực như kiến trúc, kỹ thuật, thiên văn học và cả trong các bài toán tối ưu hóa thường gặp trong đời sống hàng ngày.
Dạng 9: Bài Toán Tổ Hợp
Tổ hợp là một lĩnh vực quan trọng trong toán học, liên quan đến việc đếm, sắp xếp và chọn lựa các đối tượng theo những quy tắc nhất định. Bài toán tổ hợp thường xuất hiện trong các bài kiểm tra và thi cử, yêu cầu người học phải áp dụng linh hoạt các quy tắc tổ hợp để giải quyết.
1. Nguyên Lý Cơ Bản Của Tổ Hợp
Có hai nguyên lý cơ bản trong tổ hợp là nguyên lý cộng và nguyên lý nhân:
- Nguyên lý cộng: Nếu có \(m\) cách thực hiện một công việc và \(n\) cách thực hiện một công việc khác, không có cách nào trùng lặp, thì có tổng cộng \(m + n\) cách thực hiện một trong hai công việc.
- Nguyên lý nhân: Nếu có \(m\) cách thực hiện một công việc và \(n\) cách thực hiện một công việc khác ngay sau đó, thì có tổng cộng \(m \times n\) cách thực hiện cả hai công việc.
2. Hoán Vị
Hoán vị là một cách sắp xếp lại các đối tượng trong một tập hợp. Số hoán vị của \(n\) phần tử là:
\[ P(n) = n! = n \times (n-1) \times (n-2) \times \dots \times 1 \]
Ví dụ: Số hoán vị của 3 phần tử \(A\), \(B\), \(C\) là \(3! = 6\).
3. Chỉnh Hợp
Chỉnh hợp của \(k\) phần tử trong số \(n\) phần tử là cách chọn và sắp xếp \(k\) phần tử từ một tập hợp \(n\) phần tử. Công thức tính chỉnh hợp là:
\[ A(n, k) = \frac{n!}{(n-k)!} \]
Ví dụ: Số chỉnh hợp của 2 phần tử từ 3 phần tử \(A\), \(B\), \(C\) là \(A(3, 2) = 6\).
4. Tổ Hợp
Tổ hợp là cách chọn \(k\) phần tử từ \(n\) phần tử mà không quan tâm đến thứ tự. Công thức tính tổ hợp là:
\[ C(n, k) = \frac{n!}{k!(n-k)!} \]
Ví dụ: Số tổ hợp của 2 phần tử từ 3 phần tử \(A\), \(B\), \(C\) là \(C(3, 2) = 3\).
5. Bài Toán Ứng Dụng
Trong thực tế, bài toán tổ hợp được ứng dụng rộng rãi, chẳng hạn như:
- Tính số cách chọn đội tuyển từ một nhóm học sinh.
- Xác định số cách sắp xếp thứ tự ưu tiên của các công việc.
- Tính toán xác suất trong các trò chơi may rủi.
Thông qua việc học tập và ứng dụng các nguyên lý tổ hợp, chúng ta có thể giải quyết nhiều vấn đề phức tạp trong cuộc sống hàng ngày một cách hiệu quả.
Dạng 10: Xác Suất Thống Kê
Xác suất thống kê là một nhánh quan trọng trong toán học, giúp chúng ta hiểu và dự đoán các hiện tượng ngẫu nhiên. Bằng cách sử dụng các nguyên lý xác suất, chúng ta có thể đưa ra các phán đoán và dự đoán về những sự kiện có khả năng xảy ra trong tương lai.
Dưới đây là các bước cơ bản để giải quyết một bài toán về xác suất:
-
Xác định không gian mẫu:
Không gian mẫu (ký hiệu là \(S\)) là tập hợp tất cả các kết quả có thể xảy ra của một thí nghiệm ngẫu nhiên. Ví dụ, khi gieo một đồng xu, không gian mẫu sẽ là \(\{S = \text{“Sấp”, “Ngửa”}\}\).
-
Xác định sự kiện:
Một sự kiện (ký hiệu là \(A\)) là một tập con của không gian mẫu. Nếu một sự kiện xảy ra, thì một hoặc nhiều kết quả trong sự kiện đó sẽ xuất hiện. Ví dụ, sự kiện “xuất hiện mặt ngửa” là một tập con của không gian mẫu khi gieo đồng xu.
-
Tính xác suất của một sự kiện:
Xác suất của một sự kiện \(A\) là tỷ lệ giữa số kết quả thuận lợi cho sự kiện \(A\) và tổng số kết quả có thể trong không gian mẫu \(S\), được tính bằng công thức:
\[ P(A) = \frac{|A|}{|S|} \]Trong đó \(P(A)\) là xác suất của sự kiện \(A\), \(|A|\) là số lượng kết quả thuận lợi cho \(A\), và \(|S|\) là tổng số kết quả trong không gian mẫu \(S\).
Hãy xem một ví dụ cụ thể:
Ví dụ: Giả sử có một túi chứa 3 viên bi đỏ và 2 viên bi xanh. Nếu rút ngẫu nhiên một viên bi từ túi, xác suất để rút được viên bi đỏ là bao nhiêu?
Giải:
- Không gian mẫu \(S\): Có tổng cộng 5 viên bi, nên \(|S| = 5\).
- Sự kiện \(A\): “Rút được viên bi đỏ”. Có 3 viên bi đỏ, nên \(|A| = 3\).
- Tính xác suất: \(P(A) = \frac{3}{5} = 0.6\).
Như vậy, xác suất để rút được một viên bi đỏ là 0.6, hay 60%.
Xác suất thống kê còn được ứng dụng trong nhiều lĩnh vực khác nhau như kinh tế, y học, và khoa học xã hội. Nó giúp chúng ta đưa ra quyết định dựa trên dữ liệu và các sự kiện ngẫu nhiên.