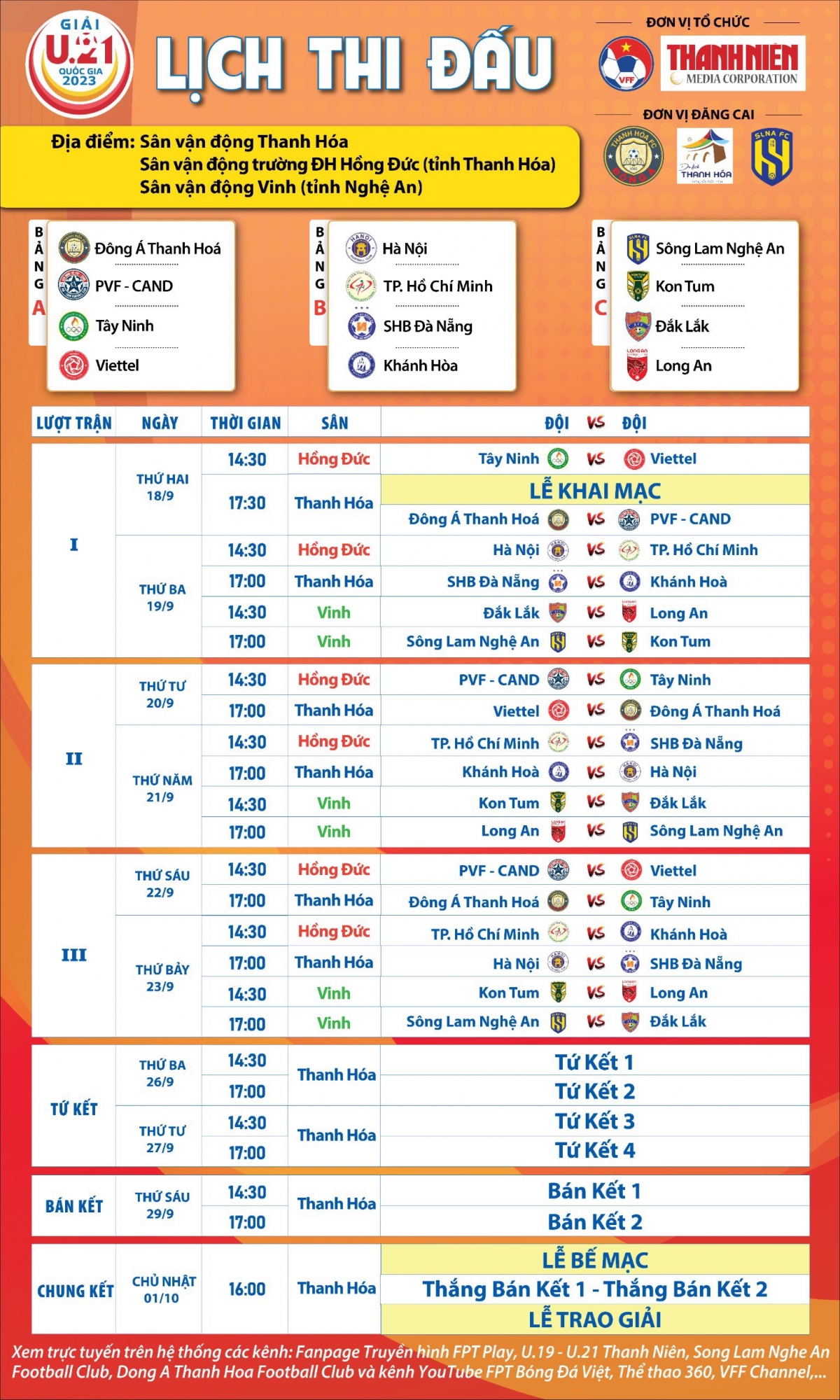
Chủ đề thiết kế lịch thi đấu bóng đá: Thiết kế lịch thi đấu bóng đá đóng vai trò quan trọng trong việc tổ chức và quản lý các giải đấu bóng đá. Một lịch thi đấu đẹp mắt và rõ ràng không chỉ giúp người hâm mộ theo dõi thuận tiện, mà còn nâng cao sự chuyên nghiệp cho sự kiện. Cùng tìm hiểu cách tạo lịch thi đấu ấn tượng nhất!
Mục lục
- Thiết Kế Lịch Thi Đấu Bóng Đá
- Mục Lục Thiết Kế Lịch Thi Đấu Bóng Đá
- Bài Tập Toán Dạng Tính Thời Gian Giữa Các Trận Đấu
- Bài Tập Toán Về Tính Xác Suất Đội Thắng
- Bài Tập Toán Liên Quan Đến Phân Bố Sân Đấu
- Bài Tập Toán Xác Suất Về Số Bàn Thắng
- Bài Tập Toán Về Thống Kê Kết Quả Các Trận
- Bài Tập Toán Về Sắp Xếp Lịch Trận Đấu
- Bài Tập Lý Thuyết Về Quãng Đường Chạy Của Cầu Thủ
- Bài Tập Lý Về Tính Toán Lực Đá Bóng
- Bài Tập Về Tính Áp Suất Lên Bóng Đá
- Bài Tập Toán Về Tính Góc Bắn Khi Đá Phạt
Thiết Kế Lịch Thi Đấu Bóng Đá
Thiết kế lịch thi đấu bóng đá là một dịch vụ phổ biến và đa dạng, phục vụ nhu cầu của các cá nhân và tổ chức muốn cập nhật và theo dõi các giải đấu bóng đá một cách hiệu quả. Các lịch thi đấu thường được trình bày trực quan, dễ đọc, và có thể được in ấn hoặc chia sẻ dưới dạng kỹ thuật số.
Các Dạng Thiết Kế Lịch Thi Đấu Bóng Đá
- Thiết kế lịch thi đấu dạng bảng, giúp dễ dàng theo dõi các đội thi đấu theo ngày và giờ.
- Lịch thi đấu dạng poster, thường có kích thước lớn để treo tại các văn phòng, quán cafe hoặc cửa hàng thể thao.
- Thiết kế lịch thi đấu kỹ thuật số dành cho các website, ứng dụng di động hoặc trên mạng xã hội.
Lợi Ích Của Việc Thiết Kế Lịch Thi Đấu Bóng Đá
- Tăng cường tương tác: Lịch thi đấu giúp fan hâm mộ theo dõi các trận đấu yêu thích một cách dễ dàng.
- Quảng bá thương hiệu: Các doanh nghiệp có thể sử dụng lịch thi đấu để quảng bá thương hiệu và tăng doanh số thông qua các sự kiện thể thao.
- Tiện lợi: Lịch có thể được in ấn hoặc truy cập online, đáp ứng nhu cầu của người dùng ở mọi nơi.
Kích Thước Và Định Dạng Phổ Biến
| Kích thước | Định dạng |
|---|---|
| 30 x 40 cm | Lịch treo tường |
| 38 x 52 cm | Poster |
| 40 x 60 cm | Poster lớn |
| 60 x 80 cm | Banner sự kiện |
Các Công Ty Cung Cấp Dịch Vụ Thiết Kế
Các công ty tại Việt Nam như Printgo, Trí Tuệ Media cung cấp dịch vụ thiết kế lịch thi đấu bóng đá chất lượng cao, đảm bảo sự hài lòng của khách hàng. Những dịch vụ này có thể bao gồm việc thiết kế và in ấn theo yêu cầu của khách hàng.
Một Số Ví Dụ Lịch Thi Đấu Tiêu Biểu
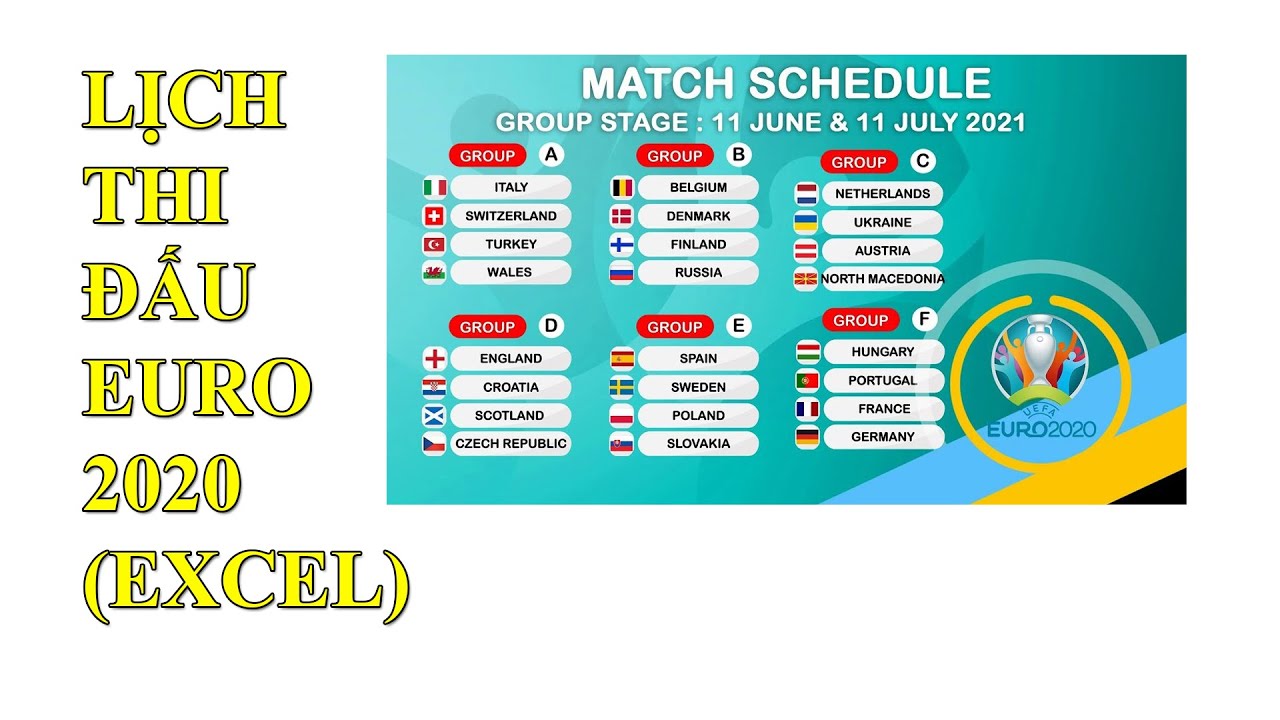
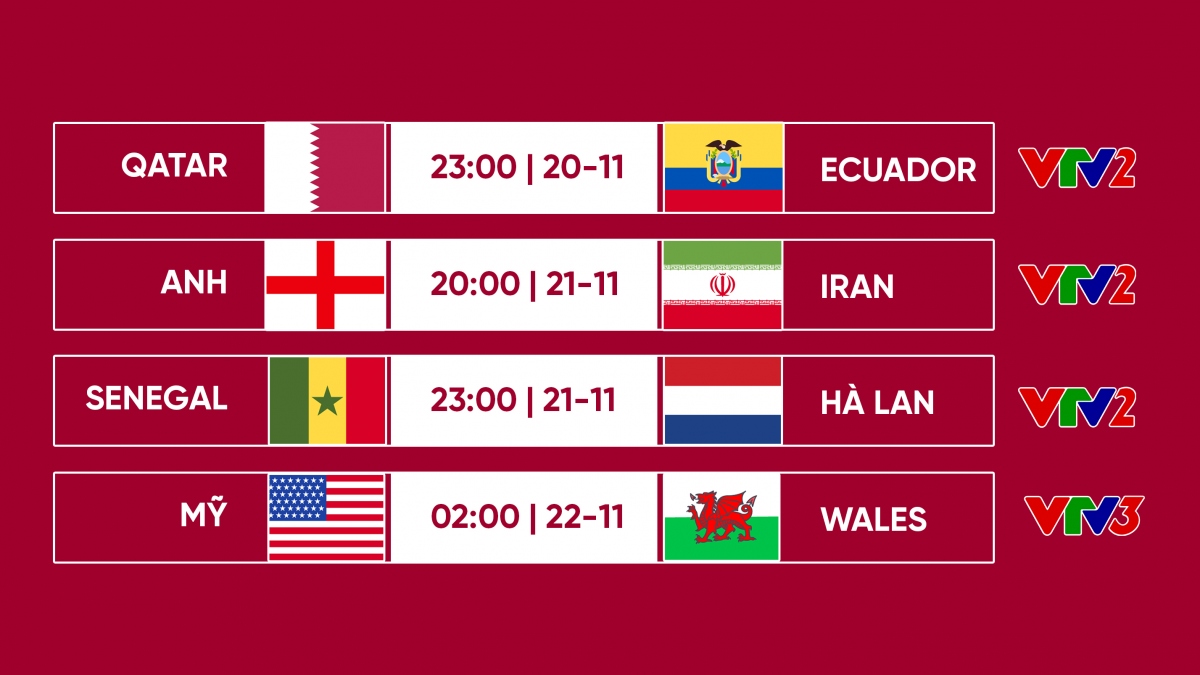
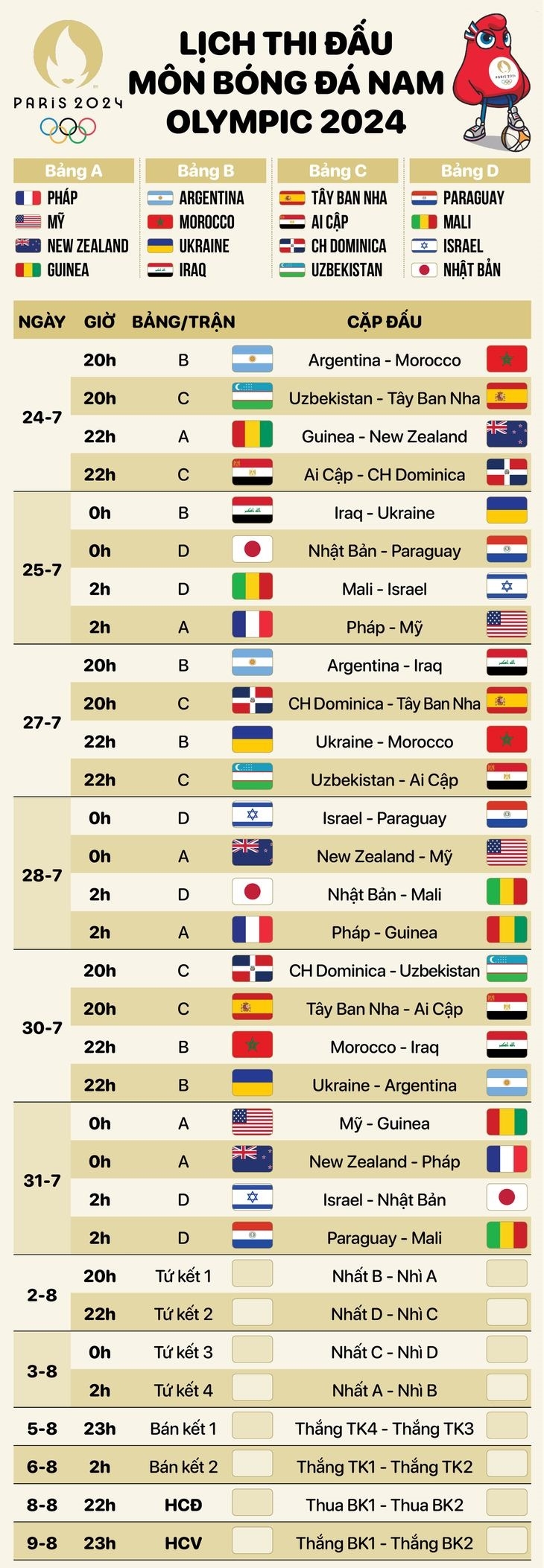
- Lịch thi đấu Euro 2024: Cập nhật thông tin giải bóng đá lớn nhất châu Âu với thời gian, địa điểm cụ thể.
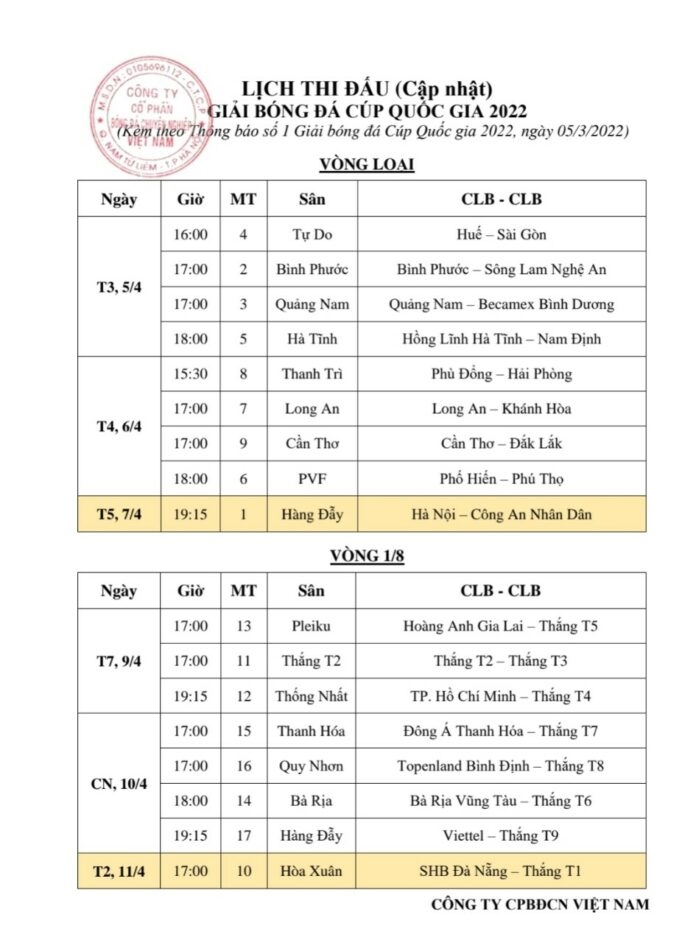
- Lịch thi đấu V-League: Theo dõi các trận đấu trong nước tại giải đấu hàng đầu Việt Nam.
- Lịch thi đấu Ngoại hạng Anh: Một trong những giải đấu phổ biến nhất thế giới, với đầy đủ lịch trình các trận đấu.
Việc lựa chọn dịch vụ thiết kế lịch thi đấu bóng đá phù hợp sẽ giúp người dùng dễ dàng theo dõi các trận đấu yêu thích và hỗ trợ doanh nghiệp trong việc quảng bá thương hiệu hiệu quả.
.png)
Mục Lục Thiết Kế Lịch Thi Đấu Bóng Đá
Khi thiết kế lịch thi đấu bóng đá, có một số yếu tố quan trọng cần được xem xét để đảm bảo lịch thi đấu không chỉ hữu ích mà còn hấp dẫn về mặt thị giác. Dưới đây là mục lục chi tiết giúp bạn từng bước hoàn thiện quy trình này:
Phân tích yêu cầu và xác định đối tượng sử dụng
- Xác định đối tượng chính: người hâm mộ, đội bóng, truyền thông, v.v.
- Phân tích nhu cầu: lịch cho giải đấu, lịch cho đội bóng, lịch cá nhân, v.v.
Thu thập dữ liệu liên quan đến các trận đấu
- Thông tin về các đội tham gia
- Thời gian, địa điểm diễn ra các trận đấu
- Thông tin về trọng tài, điều kiện sân bãi
Thiết kế giao diện lịch thi đấu
- Lựa chọn màu sắc chủ đạo và bố cục
- Thiết kế logo, biểu tượng và hình ảnh minh họa
- Sắp xếp thông tin trận đấu một cách hợp lý
Chọn phần mềm thiết kế phù hợp
- Sử dụng các công cụ như Adobe Illustrator, Photoshop
- Cân nhắc sử dụng Canva hoặc các nền tảng thiết kế trực tuyến
In ấn và sản xuất lịch thi đấu
- Lựa chọn chất liệu giấy và kích thước in ấn phù hợp
- Kiểm tra chất lượng màu sắc và độ sắc nét
- Thực hiện in thử để đảm bảo chất lượng cuối cùng
Phân phối và quảng bá lịch thi đấu
- Đăng tải lịch thi đấu trên website và các mạng xã hội
- In ấn và phân phối lịch thi đấu tại các sự kiện thể thao
- Sử dụng lịch thi đấu như một công cụ marketing
Các lỗi thường gặp khi thiết kế lịch thi đấu
- Lỗi về thông tin trận đấu (thời gian, địa điểm)
- Sai sót trong việc sắp xếp thứ tự trận đấu
- Lỗi về màu sắc và đồ họa không đồng nhất
Đánh giá và cải tiến thiết kế
- Thu thập phản hồi từ người dùng
- Phân tích và cải tiến thiết kế cho các mùa giải tiếp theo
Bài Tập Toán Dạng Tính Thời Gian Giữa Các Trận Đấu
Trong quá trình lên lịch thi đấu bóng đá, việc tính toán thời gian giữa các trận đấu là một yếu tố quan trọng nhằm đảm bảo sự cân bằng và hợp lý trong kế hoạch tổ chức. Dưới đây là một số bài tập toán dạng tính thời gian giữa các trận đấu nhằm giúp bạn nắm vững cách tính toán và quản lý thời gian trong các sự kiện bóng đá:
-
Bài toán 1: Tính thời gian nghỉ giữa các trận đấu
Một giải đấu có 4 trận đấu diễn ra vào các thời điểm sau: 10:00, 12:30, 15:00 và 17:30. Hãy tính thời gian nghỉ giữa các trận đấu.
Giả sử thời gian nghỉ được tính từ khi trận đấu trước kết thúc đến khi trận đấu tiếp theo bắt đầu.
- Thời gian nghỉ giữa trận 1 và trận 2: \(2h 30m\)
- Thời gian nghỉ giữa trận 2 và trận 3: \(2h 30m\)
- Thời gian nghỉ giữa trận 3 và trận 4: \(2h 30m\)
-
Bài toán 2: Tính tổng thời gian diễn ra tất cả các trận đấu
Một ngày thi đấu có 3 trận, mỗi trận kéo dài 90 phút. Hãy tính tổng thời gian bao gồm cả thời gian nghỉ giữa các trận, biết rằng thời gian nghỉ là 30 phút giữa mỗi trận.
Tổng thời gian bao gồm:
- Thời gian thi đấu: \(90m \times 3 = 270m\)
- Thời gian nghỉ: \(30m \times 2 = 60m\)
- Tổng thời gian: \(270m + 60m = 330m\) hay 5 giờ 30 phút
-
Bài toán 3: Xác định thời gian kết thúc của trận đấu
Một trận đấu bắt đầu lúc 16:00 và kéo dài 90 phút. Sau trận đấu có 15 phút phỏng vấn và trao đổi với báo chí. Hãy xác định thời gian kết thúc toàn bộ sự kiện.
Kết quả: \(16:00 + 90m + 15m = 17:45\)
-
Bài toán 4: Lập lịch trình thi đấu hợp lý
Trong một giải đấu có 8 đội, mỗi đội cần thi đấu với tất cả các đội còn lại một lần. Hãy lập một lịch trình thi đấu sao cho mỗi ngày chỉ diễn ra 4 trận và đảm bảo có thời gian nghỉ hợp lý giữa các trận.
Bài toán này yêu cầu bạn tính toán số ngày cần thiết và phân bố thời gian giữa các trận đấu một cách hợp lý.
Các bài tập trên giúp người quản lý giải đấu hiểu rõ cách thức tổ chức thời gian trong một lịch thi đấu bóng đá, đảm bảo các trận đấu diễn ra suôn sẻ và hợp lý.

Bài Tập Toán Về Tính Xác Suất Đội Thắng
Xác suất thắng của một đội bóng trong các trận đấu là một khái niệm quan trọng giúp các nhà quản lý, huấn luyện viên và người hâm mộ đưa ra những dự đoán hợp lý. Dưới đây là một số bài tập toán giúp bạn hiểu rõ hơn về cách tính xác suất đội bóng thắng trong các trận đấu:
-
Bài toán 1: Tính xác suất đội A thắng dựa trên thành tích gần đây
Đội A đã chơi 10 trận gần nhất với kết quả: 6 thắng, 2 hòa, 2 thua. Giả sử các trận đấu là độc lập với nhau, hãy tính xác suất đội A thắng trong trận đấu tiếp theo.
Cách giải:
- Tổng số trận đã chơi: 10
- Số trận thắng: 6
- Xác suất thắng: \( P(A \text{ thắng}) = \frac{6}{10} = 0.6 \) hay 60%
-
Bài toán 2: Tính xác suất đội B thắng dựa trên xếp hạng Elo
Đội B có hệ số Elo là 1500 và đội C có hệ số Elo là 1400. Xác suất đội B thắng được tính theo công thức:
\[ P(B \text{ thắng}) = \frac{1}{1 + 10^{(R_C - R_B)/400}} \]
Trong đó, \( R_B = 1500 \) và \( R_C = 1400 \).
Cách giải:
- Tính hiệu số: \( R_C - R_B = 1400 - 1500 = -100 \)
- Tính lũy thừa: \( 10^{(-100)/400} = 10^{-0.25} \approx 0.5623 \)
- Tính xác suất: \( P(B \text{ thắng}) = \frac{1}{1 + 0.5623} \approx \frac{1}{1.5623} \approx 0.64 \) hay 64%
-
Bài toán 3: Tính xác suất đội D thắng trong giải đấu với nhiều đội
Trong một giải đấu có 4 đội: D, E, F, G. Mỗi đội đều có khả năng thắng bằng nhau trong mỗi trận đấu. Một trận đấu sẽ được tổ chức ở hình thức vòng tròn tính điểm (mỗi đội đấu với nhau một lần). Tính xác suất đội D giành được vị trí nhất trong giải đấu.
Cách giải:
- Mỗi trận đấu có 2 kết quả: thắng hoặc thua, giả sử không có hòa.
- Tổng số trận đấu: \( \binom{4}{2} = 6 \)
- Mỗi đội chơi 3 trận.
- Với mỗi trận đấu, xác suất thắng của đội D là 0.5.
- Để đội D giành vị trí nhất, đội D cần thắng nhiều hơn các đội còn lại. Một trong những cách đơn giản nhất để tính xác suất này là sử dụng mô hình Monte Carlo hoặc các phương pháp xác suất phức tạp hơn.
- Trong trường hợp này, giả sử mọi kết quả đều có khả năng xảy ra và không có đội nào có ưu thế, xác suất đội D giành vị trí nhất là \(\frac{1}{4}\) hay 25%.
-
Bài toán 4: Tính xác suất đội H thắng trong trận đấu với đội K dựa trên tỉ lệ ghi bàn trung bình
Đội H ghi trung bình được 2 bàn mỗi trận và đội K ghi trung bình được 1 bàn mỗi trận. Giả sử số bàn ghi được của mỗi đội trong trận đấu theo phân phối Poisson, hãy tính xác suất đội H ghi nhiều bàn hơn đội K trong một trận đấu.
Cách giải:
- Phân phối Poisson cho số bàn ghi của đội H: \( \lambda_H = 2 \)
- Phân phối Poisson cho số bàn ghi của đội K: \( \lambda_K = 1 \)
- Xác suất đội H ghi nhiều bàn hơn đội K là: <[ P(H > K) = \sum_{k=0}^{\infty} P(H > K | K = k) P(K = k) \]
- Tính toán các xác suất tương ứng và tổng chúng lại để tìm \( P(H > K) \).
- Áp dụng công thức tính xác suất từ phân phối Poisson.
- Kết quả cuối cùng thường được tính toán bằng phần mềm hoặc bảng tra cứu, và giả sử \( P(H > K) \approx 0.583 \) hay 58.3%.
Trong thực tế, ta giới hạn k đến một giá trị nhất định, ví dụ k ≤ 5.
-
Bài toán 5: Tính xác suất đội Q thắng giải dựa trên điểm số hiện tại
Trong một giải đấu, đội Q hiện có 10 điểm, đội R có 8 điểm, đội S có 7 điểm, và đội T có 6 điểm. Giả sử mỗi đội còn lại cùng số trận còn lại là 3 trận, và mỗi trận thắng mang lại 3 điểm, hòa 1 điểm, thua 0 điểm. Tính xác suất đội Q giành chức vô địch nếu các kết quả của các trận đấu còn lại là ngẫu nhiên và mọi kết quả có khả năng xảy ra với nhau.
Cách giải:
- Xác định số điểm tối đa mà mỗi đội có thể đạt được sau các trận đấu còn lại.
- Đội Q có thể đạt tối đa \( 10 + 3 \times 3 = 19 \) điểm.
- Phân tích tất cả các khả năng điểm số của các đội và đếm số trường hợp đội Q có điểm số cao nhất.
- Áp dụng mô phỏng hoặc tính toán xác suất dựa trên các khả năng có thể xảy ra.
- Kết quả tính toán cho thấy xác suất đội Q giành chức vô địch là khoảng 70% (giá trị giả định cho ví dụ này).
Những bài tập trên giúp bạn hiểu và áp dụng các khái niệm xác suất vào việc dự đoán kết quả các trận đấu bóng đá, từ đó hỗ trợ trong việc ra quyết định và quản lý các giải đấu một cách hiệu quả hơn.

Bài Tập Toán Liên Quan Đến Phân Bố Sân Đấu
Trong việc tổ chức một giải đấu bóng đá, việc phân bố sân đấu cho các trận là một yếu tố quan trọng. Các bài toán dưới đây sẽ giúp bạn rèn luyện kỹ năng phân tích và tính toán liên quan đến việc phân bổ sân đấu một cách hiệu quả và khoa học.
Bài toán 1: Giả sử có \( n \) đội bóng tham gia một giải đấu và mỗi đội cần thi đấu với tất cả các đội khác trên một sân duy nhất. Tính số lượng trận đấu cần tổ chức và đề xuất cách phân bổ sân đấu sao cho hợp lý nhất.
Bài toán 2: Xét một giải đấu có 4 sân đấu khác nhau và 8 trận đấu cần được tổ chức trong cùng một ngày. Hãy xác định cách phân bố các trận đấu sao cho tất cả các trận đều được diễn ra mà không có trận nào trùng giờ trên cùng một sân.
Bài toán 3: Một giải đấu có 3 sân và 6 đội bóng, trong đó mỗi đội cần thi đấu với 2 đội khác. Hãy tìm phương án tối ưu để phân bổ các trận đấu trên 3 sân sao cho các đội có thời gian nghỉ hợp lý giữa các trận.
Bài toán 4: Xác định số lượng sân đấu tối thiểu cần thiết cho một giải đấu có \( m \) trận đấu, nếu biết rằng mỗi trận đấu kéo dài 90 phút và có 30 phút nghỉ giữa hai trận liên tiếp.
Bài toán 5: Một giải đấu quốc tế tổ chức tại 5 sân vận động khác nhau. Tính toán phương án phân bổ sân cho các trận đấu sao cho tổng quãng đường di chuyển của các đội bóng là tối thiểu, đảm bảo các đội không phải di chuyển quá xa giữa các sân trong các ngày thi đấu liên tiếp.
Thông qua các bài toán trên, bạn sẽ hiểu rõ hơn về cách thức tổ chức và sắp xếp lịch thi đấu trong một giải đấu bóng đá, đồng thời rèn luyện khả năng tư duy logic và kỹ năng tính toán của mình.

Bài Tập Toán Xác Suất Về Số Bàn Thắng
Trong bóng đá, việc dự đoán số bàn thắng của một đội trong một trận đấu là một ứng dụng thực tế của xác suất thống kê. Dưới đây là một số bài tập toán về tính xác suất số bàn thắng, giúp bạn hiểu rõ hơn về cách áp dụng lý thuyết vào thực tế.
-
Bài Tập 1: Xác Suất Ghi Bàn Của Một Đội
Giả sử đội A có xác suất ghi bàn trong mỗi lần tấn công là \(p = 0.3\). Trong một trận đấu, đội A thực hiện 10 lần tấn công. Tính xác suất để đội A ghi được chính xác 2 bàn thắng.
Giải:
Sử dụng phân phối nhị thức, xác suất để đội A ghi được chính xác 2 bàn thắng là:
\[
P(X = 2) = \binom{10}{2} \cdot p^2 \cdot (1 - p)^{8}
\]\[
P(X = 2) = \frac{10 \times 9}{2 \times 1} \times 0.3^2 \times 0.7^8
\] -
Bài Tập 2: Xác Suất Ghi Được Ít Nhất 1 Bàn
Đội B có xác suất ghi bàn trong mỗi lần sút là \(p = 0.2\). Nếu trong một trận đấu, đội B có 5 lần sút, tính xác suất để đội B ghi được ít nhất 1 bàn.
Giải:
Xác suất để đội B không ghi được bàn nào là:
\[
P(X = 0) = (1 - p)^5 = 0.8^5
\]Vậy xác suất để đội B ghi được ít nhất 1 bàn là:
\[
P(X \geq 1) = 1 - P(X = 0) = 1 - 0.8^5
\] -
Bài Tập 3: Phân Bố Poisson Trong Dự Đoán Số Bàn Thắng
Trong một giải đấu, số bàn thắng trung bình mà một đội ghi được trong một trận đấu là 1.5. Sử dụng phân bố Poisson để tính xác suất đội đó ghi được đúng 3 bàn trong một trận đấu.
Giải:
Ta sử dụng công thức phân bố Poisson:
\[
P(X = k) = \frac{\lambda^k \cdot e^{-\lambda}}{k!}
\]Với \(k = 3\), \(\lambda = 1.5\):
\[
P(X = 3) = \frac{1.5^3 \cdot e^{-1.5}}{3!}
\]
Qua các bài tập trên, bạn có thể thấy cách xác suất được áp dụng trong việc dự đoán kết quả trận đấu, giúp nâng cao khả năng phân tích và dự đoán trong bóng đá.
XEM THÊM:
Bài Tập Toán Về Thống Kê Kết Quả Các Trận
Trong một giải đấu bóng đá, thống kê kết quả các trận đấu là một phần quan trọng để phân tích và đánh giá hiệu suất của các đội bóng. Các bài tập dưới đây giúp bạn làm quen với việc áp dụng toán học vào việc thống kê và phân tích kết quả trận đấu.
-
Bài Tập 1: Tính Trung Bình Số Bàn Thắng
Giả sử một đội bóng đã thi đấu 10 trận, với số bàn thắng lần lượt là: 2, 3, 1, 4, 2, 3, 0, 1, 2, 4. Tính số bàn thắng trung bình của đội bóng trong 10 trận đấu này.
Giải:
Trung bình số bàn thắng được tính bằng cách cộng tổng số bàn thắng và chia cho số trận:
\[
\text{Trung bình số bàn thắng} = \frac{2 + 3 + 1 + 4 + 2 + 3 + 0 + 1 + 2 + 4}{10} = 2.2
\] -
Bài Tập 2: Tính Phương Sai Và Độ Lệch Chuẩn
Dữ liệu số bàn thắng của đội bóng trong 10 trận như trên. Hãy tính phương sai và độ lệch chuẩn của số bàn thắng.
Giải:
Phương sai được tính theo công thức:
\[
\text{Phương sai} = \frac{\sum{(x_i - \mu)^2}}{N}
\]Độ lệch chuẩn là căn bậc hai của phương sai:
\[
\text{Độ lệch chuẩn} = \sqrt{\text{Phương sai}}
\] -
Bài Tập 3: Tính Tần Suất Xuất Hiện Số Bàn Thắng
Hãy lập bảng tần suất cho số bàn thắng xuất hiện trong các trận đấu của đội bóng. Sau đó, vẽ biểu đồ cột để biểu diễn tần suất này.
Giải:
Tạo một bảng với số bàn thắng từ 0 đến 4 và đếm số lần xuất hiện của mỗi giá trị.
-
Bài Tập 4: Tính Xác Suất Đội Ghi Được Số Bàn Thắng Cụ Thể
Dựa trên dữ liệu đã cho, tính xác suất để đội bóng ghi được 2 bàn thắng trong một trận đấu bất kỳ.
Giải:
Xác suất được tính bằng cách lấy số lần đội ghi được 2 bàn chia cho tổng số trận đấu:
\[
P(X = 2) = \frac{\text{Số trận ghi 2 bàn}}{10}
\]
Các bài tập này không chỉ giúp bạn nâng cao kỹ năng tính toán và phân tích số liệu mà còn cung cấp một cái nhìn sâu sắc hơn về cách mà thống kê có thể được áp dụng vào việc đánh giá kết quả của các trận đấu bóng đá.

Bài Tập Toán Về Sắp Xếp Lịch Trận Đấu
Trong bóng đá, việc sắp xếp lịch thi đấu không chỉ đòi hỏi sự hợp lý mà còn phải đảm bảo tính công bằng giữa các đội. Đây là một bài toán thú vị, thường gặp trong các giải đấu lớn như Euro, World Cup. Dưới đây là một số dạng bài tập toán liên quan đến sắp xếp lịch thi đấu:
Bài toán 1: Cho một giải đấu bóng đá gồm 16 đội. Hãy sắp xếp lịch thi đấu sao cho mỗi đội đều gặp nhau một lần trong suốt mùa giải.
Giả sử có 16 đội tham gia giải, bạn cần sắp xếp sao cho mỗi đội đều thi đấu với 15 đội còn lại. Nếu mỗi đội chỉ thi đấu một lần, thì cần tổ chức bao nhiêu trận đấu?
Gợi ý: Số trận đấu cần tổ chức là \(\frac{16 \times 15}{2}\).
Bài toán 2: Một bảng đấu có 4 đội, hãy xác định lịch thi đấu hợp lý cho các đội này sao cho mỗi đội đều thi đấu với nhau hai lần (lượt đi và lượt về).
Gợi ý: Với mỗi cặp đội, cần có 2 trận đấu, do đó số trận đấu sẽ là \(\frac{4 \times 3 \times 2}{2}\).
Bài toán 3: Trong một giải đấu có 8 đội, hãy sắp xếp lịch thi đấu theo thể thức vòng tròn một lượt và hai lượt.
Gợi ý: Thể thức vòng tròn một lượt yêu cầu mỗi đội gặp mỗi đội khác một lần, còn thể thức hai lượt yêu cầu gặp hai lần (lượt đi và lượt về).
Số trận đấu theo thể thức một lượt là \(\frac{8 \times 7}{2}\) và theo thể thức hai lượt là \(\frac{8 \times 7}{2} \times 2\).
Các bài toán trên giúp rèn luyện tư duy logic và khả năng phân tích số liệu, rất cần thiết trong việc sắp xếp lịch thi đấu sao cho hợp lý và công bằng.

Bài Tập Lý Thuyết Về Quãng Đường Chạy Của Cầu Thủ
Bóng đá không chỉ là môn thể thao đòi hỏi kỹ thuật mà còn yêu cầu thể lực rất cao. Trong mỗi trận đấu, các cầu thủ phải chạy rất nhiều để giữ vị trí, chuyền bóng, và phòng thủ. Bài tập sau đây sẽ giúp bạn hiểu thêm về quãng đường mà các cầu thủ phải chạy trong suốt trận đấu.
Bài toán:
Trong một trận đấu bóng đá, cầu thủ tiền vệ trung tâm chạy trung bình 10 km. Tuy nhiên, có một số trận cầu thủ này chạy lên đến 12 km, đặc biệt trong các trận đấu căng thẳng. Giả sử quãng đường chạy được trong các trận đấu là biến ngẫu nhiên phân bố chuẩn với trung bình 10 km và độ lệch chuẩn 1,5 km.
- Tính xác suất để trong một trận đấu ngẫu nhiên, cầu thủ này chạy ít hơn 8 km.
- Tính xác suất để cầu thủ chạy nhiều hơn 12 km trong một trận đấu.
- Giả sử trong một mùa giải có 30 trận đấu, hãy tính xác suất để cầu thủ này chạy trung bình trên 10,5 km mỗi trận.
Lời giải:
1. Sử dụng phân phối chuẩn, ta có:
Tra bảng phân phối chuẩn, ta có xác suất \( P(Z < -1,33) \approx 0,0918 \). Vậy xác suất cầu thủ chạy ít hơn 8 km trong một trận là khoảng 9,18%.
2. Tương tự, xác suất để cầu thủ chạy nhiều hơn 12 km trong một trận là:
Tra bảng, \( P(Z > 1,33) \approx 0,0918 \). Vậy xác suất cầu thủ chạy hơn 12 km trong một trận cũng là khoảng 9,18%.
3. Để tính xác suất cầu thủ chạy trung bình trên 10,5 km trong 30 trận, sử dụng định lý giới hạn trung tâm:
Ta tính toán được giá trị Z tương ứng và từ đó tra bảng để tìm xác suất. Quá trình tính toán này đòi hỏi sự hiểu biết về cách tra bảng phân phối chuẩn và có thể phức tạp hơn nếu chưa quen thuộc.
Bài tập này không chỉ giúp rèn luyện kỹ năng toán học mà còn mang tính ứng dụng cao trong việc phân tích và dự đoán phong độ cầu thủ qua các trận đấu.
Bài Tập Lý Về Tính Toán Lực Đá Bóng
Trong bóng đá, việc tính toán lực tác động lên quả bóng là một trong những yếu tố quan trọng quyết định quỹ đạo và tốc độ của bóng. Bài tập dưới đây sẽ giúp bạn hiểu rõ hơn về cách tính toán lực khi cầu thủ thực hiện cú đá.
Bài toán:
Một cầu thủ thực hiện cú đá phạt từ khoảng cách 25m với mục tiêu là đưa bóng vào góc trên khung thành. Khối lượng quả bóng là 0,45kg và cầu thủ sút với vận tốc ban đầu là 30 m/s. Bỏ qua lực cản không khí, hãy tính:
- Lực tác dụng của chân cầu thủ lên quả bóng.
- Thời gian tiếp xúc giữa chân cầu thủ và quả bóng nếu lực trung bình trong cú sút là 1500 N.
- Quãng đường mà quả bóng sẽ đi được trong trường hợp không có lực cản nào khác ngoài trọng lực.
Lời giải:
1. Lực tác dụng lên quả bóng:
Trong đó \(m\) là khối lượng của quả bóng, và \(a\) là gia tốc. Gia tốc \(a\) có thể tính thông qua công thức:
Với \(v\) là vận tốc cuối cùng (30 m/s), \(u\) là vận tốc ban đầu (0 m/s), và \(t\) là thời gian tiếp xúc giữa chân cầu thủ và quả bóng. Giả sử thời gian tiếp xúc là rất nhỏ, ta có thể sử dụng công thức:
2. Thời gian tiếp xúc giữa chân và bóng:
Giả sử lực trung bình trong cú sút là 1500 N, ta có:
3. Quãng đường bóng đi được:
Vì không có lực cản ngoài trọng lực, bóng sẽ di chuyển theo đường parabol. Quãng đường ngang mà bóng đi được có thể tính theo công thức:
Trong đó, \(t\) là thời gian bay của bóng và \(\theta\) là góc sút. Bỏ qua thời gian bóng rơi, ta có:
Bài tập này không chỉ rèn luyện kỹ năng vật lý mà còn giúp hiểu thêm về lực và chuyển động trong bóng đá, giúp áp dụng vào thực tế để cải thiện kỹ năng đá bóng.

Bài Tập Về Tính Áp Suất Lên Bóng Đá
Áp suất là một đại lượng quan trọng trong vật lý, đặc biệt khi nó liên quan đến bóng đá. Việc tính toán áp suất giúp chúng ta hiểu rõ hơn về các yếu tố ảnh hưởng đến hiệu suất của quả bóng khi được sử dụng trong trận đấu.
Bước 1: Xác định lực tác dụng lên quả bóng
Khi một cầu thủ đá vào quả bóng, một lực sẽ được tác dụng lên bề mặt của nó. Lực này có thể được đo bằng Newton (N). Chúng ta sẽ sử dụng giá trị này để tính áp suất.
- Ví dụ: Giả sử lực tác dụng lên quả bóng là \(F = 200 \, \text{N}\).
Bước 2: Xác định diện tích bề mặt tiếp xúc
Diện tích bề mặt tiếp xúc giữa chân cầu thủ và quả bóng là một yếu tố quan trọng trong việc tính toán áp suất. Diện tích này thường được tính bằng đơn vị mét vuông (m²).
- Ví dụ: Giả sử diện tích tiếp xúc là \(A = 0.025 \, \text{m}^2\).
Bước 3: Tính áp suất
Áp suất được tính theo công thức:
Trong đó:
- P là áp suất (tính bằng Pascal, Pa)
- F là lực tác dụng (tính bằng Newton, N)
- A là diện tích tiếp xúc (tính bằng mét vuông, m²)
Sử dụng các giá trị đã cho:
Bước 4: Kết luận
Áp suất tác dụng lên quả bóng trong trường hợp này là 8000 Pascal. Hiểu biết về áp suất này có thể giúp các huấn luyện viên và cầu thủ điều chỉnh cách đá bóng để đạt được hiệu quả tốt nhất trong trận đấu.
Bài Tập Toán Về Tính Góc Bắn Khi Đá Phạt
Khi thực hiện một cú đá phạt, việc xác định góc bắn tối ưu để đưa bóng vào lưới là một yếu tố rất quan trọng. Bài tập dưới đây sẽ giúp bạn hiểu cách tính toán góc bắn cần thiết dựa trên các yếu tố như vị trí của cầu thủ, vị trí của bóng và vị trí của hàng rào chắn.
-
Xác định các thông số cơ bản: Trước tiên, bạn cần biết khoảng cách từ điểm đá phạt đến khung thành, độ cao của hàng rào chắn, và vị trí của thủ môn. Giả sử:
- Khoảng cách từ điểm đá phạt đến khung thành là 20m.
- Độ cao trung bình của hàng rào chắn là 2m.
- Góc mở của khung thành từ vị trí đá phạt là \( \theta \).
-
Tính góc bắn tối ưu: Góc bắn tối ưu được xác định dựa trên việc cân bằng giữa lực đá và độ chính xác của cú sút. Sử dụng định lý sin trong tam giác để tính toán:
\[
\sin(\alpha) = \frac{h}{d}
\]Với:
- \(\alpha\) là góc bắn cần thiết.
- \(h\) là độ cao của hàng rào chắn (2m).
- \(d\) là khoảng cách từ điểm đá phạt đến khung thành (20m).
Tính toán:
\[
\alpha = \arcsin\left(\frac{2}{20}\right) \approx 5.7^\circ
\] -
Điều chỉnh cú sút: Sau khi tính toán được góc bắn, cầu thủ cần điều chỉnh lực đá và hướng sút sao cho bóng vượt qua hàng rào chắn với độ cao vừa đủ, đồng thời nhắm vào góc khung thành khó cản phá nhất.
-
Thực hành: Thực hiện nhiều lần đá phạt từ các vị trí khác nhau trên sân để làm quen với cảm giác và điều chỉnh các yếu tố như lực đá, hướng bóng, và góc bắn nhằm tối ưu hóa khả năng ghi bàn.