Chủ đề lịch thi đấu bóng đá việt nam chiều nay: Lịch thi đấu bóng đá Việt Nam chiều nay luôn thu hút sự quan tâm của người hâm mộ. Cập nhật ngay thông tin về các trận đấu, giờ thi đấu, và các đội bóng tham gia để không bỏ lỡ những khoảnh khắc hấp dẫn trên sân cỏ. Xem ngay để cổ vũ cho đội bóng yêu thích của bạn!
Mục lục
- Lịch Thi Đấu Bóng Đá Việt Nam Chiều Nay
- Mục Lục Tổng Hợp Các Kết Quả Tìm Kiếm
- Bài Tập Toán Dành Cho Học Sinh Cấp 3
- Bài Tập Vật Lý Đặc Sắc Kèm Lời Giải Chi Tiết
- Bài Tập Tiếng Anh Về Các Thì Trong Tiếng Anh
- Bài Tập Toán Giải Hệ Phương Trình
- Bài Tập Vật Lý Về Động Lực Học
- Bài Tập Tiếng Anh Về Câu Điều Kiện
- Bài Tập Toán Hình Học Không Gian
- Bài Tập Vật Lý Về Nhiệt Học
- Bài Tập Tiếng Anh Về Các Loại Câu Hỏi
- Bài Tập Toán Về Tích Phân
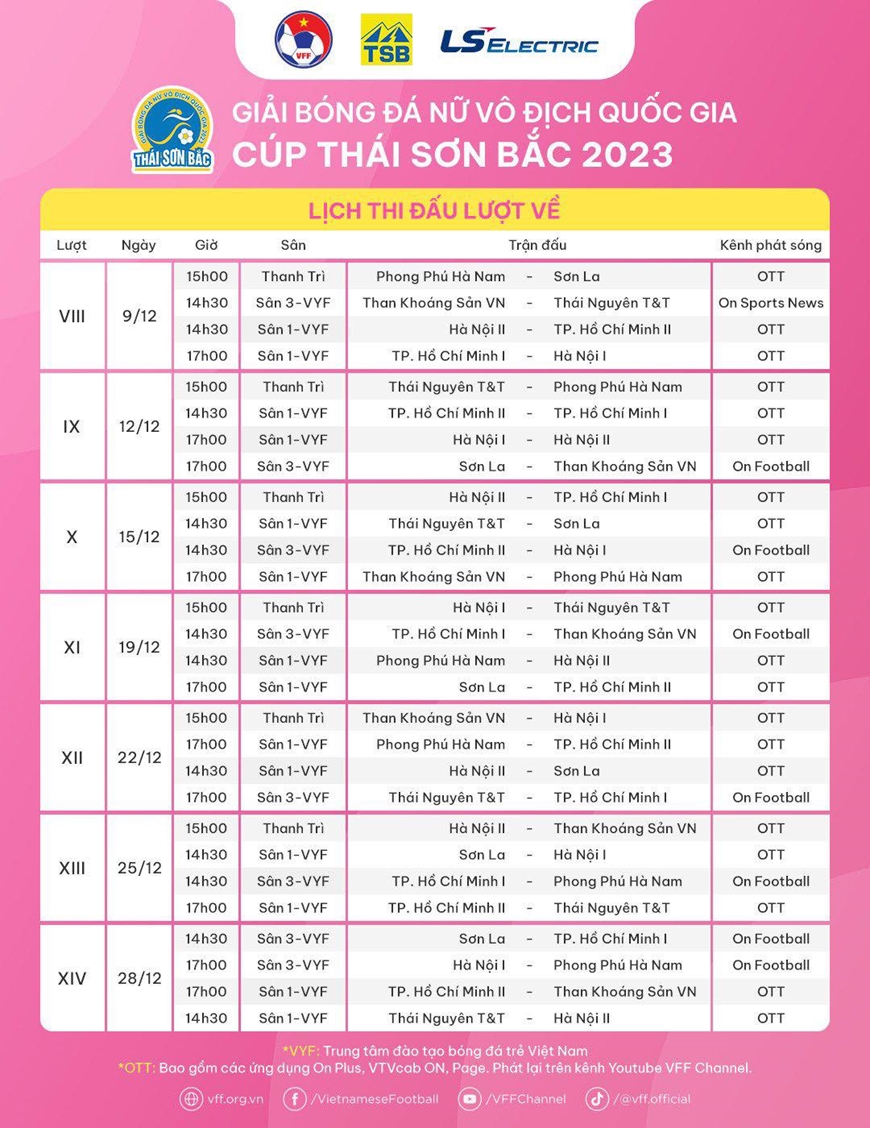
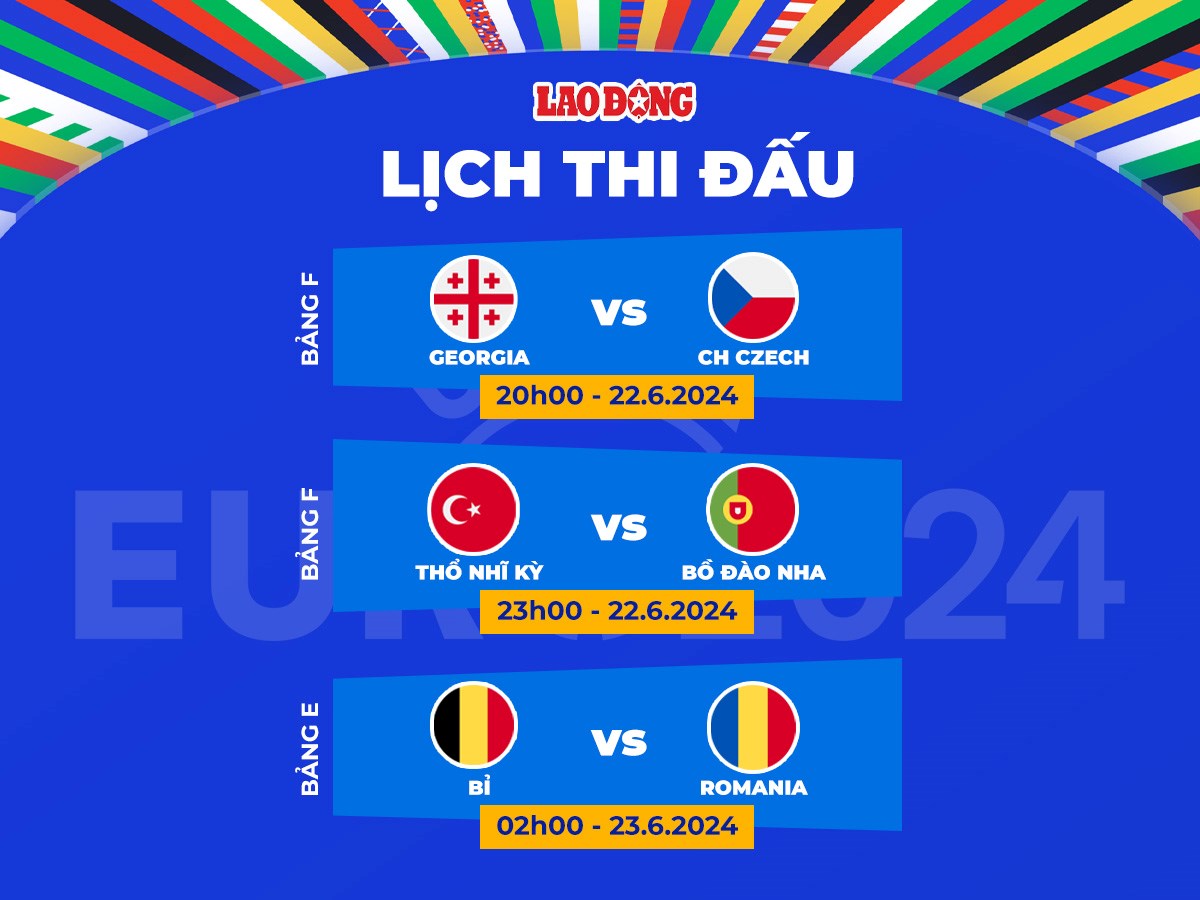
Lịch Thi Đấu Bóng Đá Việt Nam Chiều Nay
Dưới đây là thông tin chi tiết về các trận đấu bóng đá của các đội tuyển Việt Nam sẽ diễn ra trong chiều nay. Lịch thi đấu bao gồm các trận đấu của các đội tuyển quốc gia, U23, và các câu lạc bộ hàng đầu trong nước.
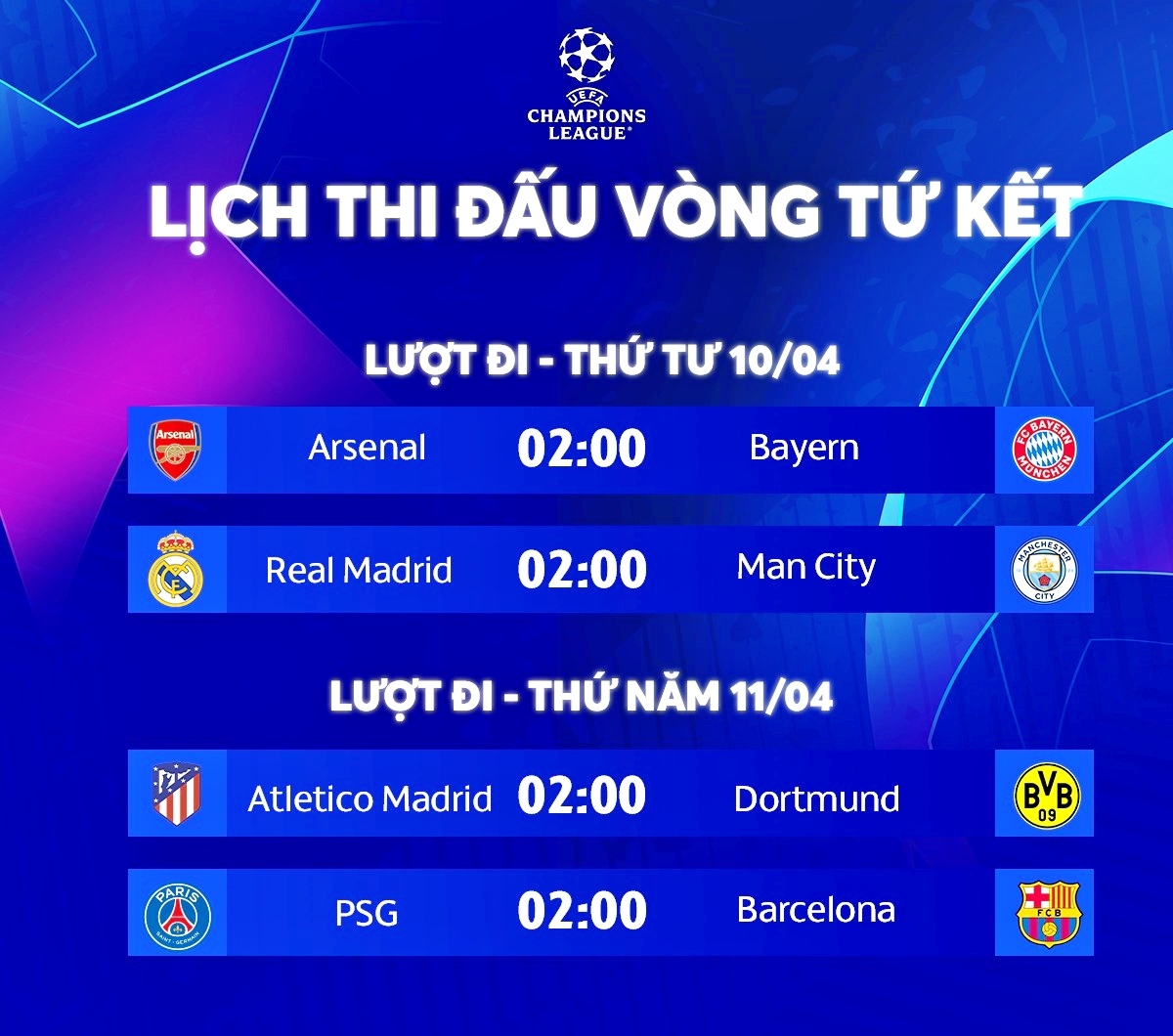
Trận Đấu Quốc Tế
- Thời gian: 16:00
- Đội tuyển: U23 Việt Nam vs U23 Indonesia
- Giải đấu: Vòng loại U23 châu Á
- Kênh truyền hình: VTV5, VTV6
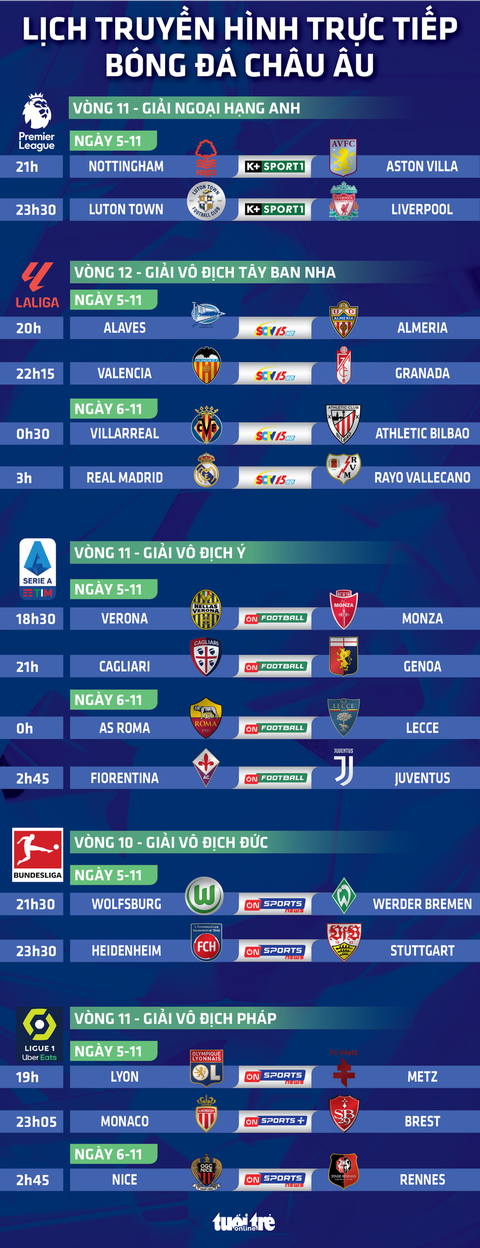
V-League
- Thời gian: 17:00
- Đội tuyển: Hà Nội FC vs Hoàng Anh Gia Lai
- Địa điểm: Sân vận động Hàng Đẫy
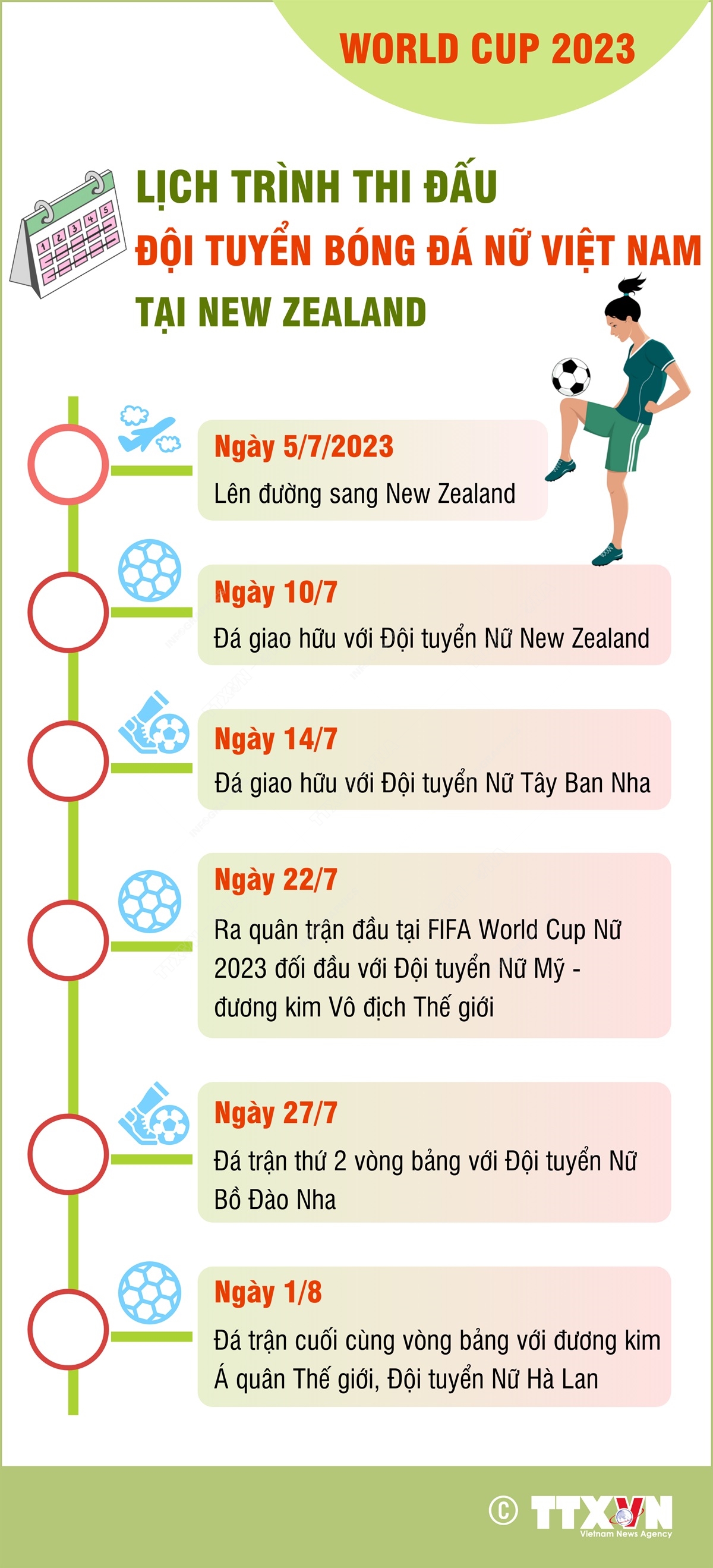
Giải Bóng Đá Nữ
- Thời gian: 19:30
- Đội tuyển: Nữ Việt Nam vs Nữ Thái Lan
- Giải đấu: Vòng loại Asian Cup Nữ
Tóm Tắt
Trong chiều nay, người hâm mộ bóng đá Việt Nam sẽ được thưởng thức nhiều trận đấu hấp dẫn từ các đội tuyển quốc gia và câu lạc bộ hàng đầu. Đừng bỏ lỡ cơ hội cổ vũ cho đội bóng yêu thích của bạn!

.png)
Mục Lục Tổng Hợp Các Kết Quả Tìm Kiếm
Dưới đây là tổng hợp chi tiết các nội dung quan trọng từ kết quả tìm kiếm với từ khóa "lịch thi đấu bóng đá việt nam chiều nay". Bài viết sẽ giúp bạn nắm bắt toàn bộ thông tin về các trận đấu, lịch thi đấu và những cập nhật quan trọng từ các nguồn đáng tin cậy.
- Lịch Thi Đấu Đội Tuyển Quốc Gia:
- Lịch thi đấu chi tiết của đội tuyển Việt Nam trong các giải đấu quốc tế.
- Thông tin các trận đấu giao hữu, chính thức và thời gian cụ thể.
- Lịch Thi Đấu V-League:
- Cập nhật lịch thi đấu mới nhất của giải V-League, bao gồm các trận đấu quan trọng chiều nay.
- Kết quả các trận đấu gần đây và bảng xếp hạng.
- Giải Bóng Đá Nữ:
- Lịch thi đấu của đội tuyển bóng đá nữ Việt Nam trong các giải đấu quốc tế.
- Thông tin về các trận đấu của giải Vô Địch Bóng Đá Nữ Quốc Gia.
- Lịch Thi Đấu Cúp Quốc Gia:
- Lịch thi đấu chi tiết các trận đấu tại Cúp Quốc Gia Việt Nam.
- Kết quả, thông tin đội bóng tham gia và sân vận động tổ chức.
- Lịch Thi Đấu Các Giải Đấu Trẻ:
- Lịch thi đấu của đội tuyển U23, U19 và các giải đấu trẻ quốc gia.
- Các trận đấu đáng chú ý và thông tin về đội bóng tham gia.
- Giải Đấu Quốc Tế Có Đội Tuyển Việt Nam Tham Gia:
- Lịch thi đấu và thông tin các giải đấu quốc tế mà đội tuyển Việt Nam tham gia.
- Các thông tin liên quan đến việc thi đấu tại nước ngoài và các trận giao hữu quốc tế.
Bài Tập Toán Dành Cho Học Sinh Cấp 3
Dưới đây là các dạng bài tập toán dành cho học sinh cấp 3, được phân chia theo từng chuyên đề và có lời giải chi tiết. Mỗi bài tập được thiết kế để rèn luyện khả năng tư duy và giải quyết vấn đề, đồng thời giúp các em củng cố kiến thức và chuẩn bị tốt cho các kỳ thi quan trọng.
- Hệ Phương Trình Bậc Nhất Hai Ẩn
Giải hệ phương trình sau:
\[ \begin{cases} 2x + 3y = 7 \\ 4x - y = 5 \end{cases} \]Lời giải chi tiết:
- Bước 1: Nhân phương trình thứ hai với 3 để loại bỏ y.
- Bước 2: Giải phương trình bậc nhất với x.
- Bước 3: Thay giá trị của x vào một trong hai phương trình để tìm y.
- Phương Trình Bậc Hai Một Ẩn
Giải phương trình sau:
\[ x^2 - 5x + 6 = 0 \]Lời giải chi tiết:
- Bước 1: Tính \(\Delta = b^2 - 4ac\).
- Bước 2: Tìm nghiệm của phương trình bằng công thức nghiệm.
- Bước 3: Kết luận nghiệm.
- Hàm Số Bậc Ba
Xét tính đơn điệu của hàm số:
\[ f(x) = x^3 - 3x + 2 \]Lời giải chi tiết:
- Bước 1: Tính đạo hàm \(f'(x)\).
- Bước 2: Giải phương trình \(f'(x) = 0\) để tìm các điểm cực trị.
- Bước 3: Dựa vào dấu của \(f'(x)\) để xác định khoảng đơn điệu.
- Hàm Số Lượng Giác
Giải phương trình lượng giác sau:
\[ \sin x + \cos x = \frac{1}{2} \]Lời giải chi tiết:
- Bước 1: Sử dụng công thức hạ bậc để đưa phương trình về dạng cơ bản.
- Bước 2: Giải phương trình và tìm các giá trị của \(x\) trong khoảng xác định.
- Hệ Phương Trình Tuyến Tính
Giải hệ phương trình sau:
\[ \begin{cases} 3x + 4y - z = 7 \\ 2x - y + 5z = 3 \\ x + 3y + 2z = 4 \end{cases} \]Lời giải chi tiết:
- Bước 1: Sử dụng phương pháp thế hoặc cộng đại số để giải hệ phương trình.
- Bước 2: Tìm nghiệm và kiểm tra lại kết quả.
- Tích Phân Hàm Số Bậc Nhất
Tính tích phân sau:
\[ \int (3x + 2) \, dx \]Lời giải chi tiết:
- Bước 1: Áp dụng công thức tích phân cơ bản.
- Bước 2: Tính kết quả và cộng hằng số tích phân \(C\).
- Đạo Hàm Hàm Số Mũ
Tính đạo hàm của hàm số sau:
\[ y = e^{2x} \cdot \ln x \]Lời giải chi tiết:
- Bước 1: Áp dụng quy tắc đạo hàm tích.
- Bước 2: Tính đạo hàm từng phần và kết hợp lại.
- Phương Trình Mũ và Logarit
Giải phương trình sau:
\[ 2^x = \log_2 (x + 3) \]Lời giải chi tiết:
- Bước 1: Đưa phương trình về cùng cơ số.
- Bước 2: Giải phương trình và tìm các giá trị của \(x\).
- Phương Trình Hypebol
Giải phương trình sau:
\[ \sinh x = 2 \]Lời giải chi tiết:
- Bước 1: Sử dụng công thức của hàm hypebol để giải phương trình.
- Bước 2: Tìm nghiệm và biểu diễn dưới dạng logarit.
- Đa Thức Bậc Ba
Phân tích đa thức sau thành nhân tử:
\[ P(x) = x^3 - 6x^2 + 11x - 6 \]Lời giải chi tiết:
- Bước 1: Sử dụng phương pháp phân tích nhân tử.
- Bước 2: Tìm các nghiệm của đa thức.

Bài Tập Vật Lý Đặc Sắc Kèm Lời Giải Chi Tiết
Dưới đây là một số bài tập vật lý đặc sắc dành cho học sinh cấp 3, được kèm theo lời giải chi tiết để các em có thể nắm vững kiến thức và áp dụng vào các kỳ thi.
Bài 1: Tính công của lực
Một vật có khối lượng \( m = 5 \, \text{kg} \) được kéo lên một dốc nghiêng không ma sát với góc nghiêng \( \alpha = 30^\circ \) so với mặt phẳng ngang. Lực kéo \( F = 50 \, \text{N} \) có phương song song với mặt phẳng nghiêng. Tính công của lực kéo sau khi vật di chuyển được quãng đường \( s = 10 \, \text{m} \).
- Phân tích bài toán: Công của lực \( F \) khi vật di chuyển được quãng đường \( s \) trên mặt phẳng nghiêng là: \( A = F \cdot s \cdot \cos\theta \).
- Tính toán:
- Góc giữa lực kéo và phương di chuyển là \( \theta = 0^\circ \), do lực kéo song song với mặt phẳng nghiêng.
- Vậy công của lực là: \[ A = F \cdot s \cdot \cos 0^\circ = 50 \, \text{N} \cdot 10 \, \text{m} \cdot 1 = 500 \, \text{J} \]
- Kết quả: Công của lực kéo là \( 500 \, \text{J} \).
Bài 2: Định luật bảo toàn cơ năng
Một viên bi có khối lượng \( m = 0.2 \, \text{kg} \) được thả rơi tự do từ độ cao \( h = 5 \, \text{m} \) so với mặt đất. Bỏ qua lực cản không khí, tính vận tốc của viên bi khi chạm đất.
- Phân tích bài toán: Theo định luật bảo toàn cơ năng, thế năng tại vị trí ban đầu sẽ chuyển hóa hoàn toàn thành động năng khi viên bi chạm đất.
- Tính toán:
- Thế năng ban đầu của viên bi: \[ W_t = m \cdot g \cdot h = 0.2 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 \cdot 5 \, \text{m} = 9.8 \, \text{J} \]
- Động năng tại thời điểm chạm đất: \[ W_d = \frac{1}{2} \cdot m \cdot v^2 \]
- Theo định luật bảo toàn cơ năng: \[ W_t = W_d \Rightarrow 9.8 \, \text{J} = \frac{1}{2} \cdot 0.2 \, \text{kg} \cdot v^2 \Rightarrow v^2 = \frac{9.8 \, \text{J}}{0.1 \, \text{kg}} = 98 \, \text{m}^2/\text{s}^2 \]
- Vận tốc của viên bi khi chạm đất: \[ v = \sqrt{98 \, \text{m}^2/\text{s}^2} \approx 9.9 \, \text{m/s} \]
- Kết quả: Vận tốc của viên bi khi chạm đất là \( 9.9 \, \text{m/s} \).
Bài 3: Bài tập về chuyển động tròn đều
Một vật có khối lượng \( m = 2 \, \text{kg} \) chuyển động tròn đều với bán kính \( r = 0.5 \, \text{m} \) và vận tốc góc \( \omega = 4 \, \text{rad/s} \). Tính lực hướng tâm tác dụng lên vật.
- Phân tích bài toán: Lực hướng tâm \( F_{ht} \) giữ cho vật chuyển động tròn đều được tính bằng công thức \( F_{ht} = m \cdot \omega^2 \cdot r \).
- Tính toán:
- Lực hướng tâm: \[ F_{ht} = 2 \, \text{kg} \cdot (4 \, \text{rad/s})^2 \cdot 0.5 \, \text{m} = 16 \, \text{N} \]
- Kết quả: Lực hướng tâm tác dụng lên vật là \( 16 \, \text{N} \).

Bài Tập Tiếng Anh Về Các Thì Trong Tiếng Anh
Dưới đây là một số bài tập tiếng Anh giúp bạn củng cố và luyện tập về các thì trong tiếng Anh, bao gồm thì hiện tại đơn, thì hiện tại tiếp diễn, thì quá khứ đơn, thì quá khứ tiếp diễn, thì tương lai đơn và thì hiện tại hoàn thành. Mỗi bài tập đi kèm với lời giải chi tiết để giúp bạn nắm vững kiến thức một cách hiệu quả.
-
Bài Tập 1: Chọn dạng đúng của động từ trong ngoặc.
- She (go) to school every day.
- They (play) football now.
- We (eat) dinner when the phone rang.
- He (finish) his homework by 10 PM yesterday.
- I (travel) to Japan next year.
Đáp án:
- She goes to school every day. (Thì hiện tại đơn)
- They are playing football now. (Thì hiện tại tiếp diễn)
- We were eating dinner when the phone rang. (Thì quá khứ tiếp diễn)
- He had finished his homework by 10 PM yesterday. (Thì quá khứ hoàn thành)
- I will travel to Japan next year. (Thì tương lai đơn)
-
Bài Tập 2: Viết lại câu sử dụng thì thích hợp.
- She usually drinks coffee in the morning. (hiện tại hoàn thành)
- They are watching a movie. (quá khứ đơn)
- I have read that book. (quá khứ đơn)
- We will go to the market. (hiện tại tiếp diễn)
Đáp án:
- She has usually drunk coffee in the morning.
- They watched a movie.
- I read that book.
- We are going to the market.
-
Bài Tập 3: Điền vào chỗ trống với thì thích hợp của động từ.
- By the time you arrive, we (finish) the project.
- He (not/see) his friends since he moved to another city.
- They (visit) the museum tomorrow.
- I (be) at home when you called.
Đáp án:
- By the time you arrive, we will have finished the project. (Thì tương lai hoàn thành)
- He has not seen his friends since he moved to another city. (Thì hiện tại hoàn thành)
- They will visit the museum tomorrow. (Thì tương lai đơn)
- I was at home when you called. (Thì quá khứ đơn)

Bài Tập Toán Giải Hệ Phương Trình
Dưới đây là một số bài tập toán giúp bạn rèn luyện kỹ năng giải hệ phương trình, bao gồm hệ phương trình bậc nhất hai ẩn, hệ phương trình đối xứng, và hệ phương trình chứa tham số. Mỗi bài tập đều có lời giải chi tiết để giúp bạn hiểu rõ phương pháp giải.
-
Bài Tập 1: Giải hệ phương trình bậc nhất hai ẩn
Giải hệ phương trình sau:
\[ \begin{cases} 2x + 3y = 6 \\ 4x - y = 5 \end{cases} \]Giải:
Giải phương trình thứ hai để tìm \( y \):
\[ y = 4x - 5 \]Thay \( y \) vào phương trình thứ nhất:
\[ 2x + 3(4x - 5) = 6 \]Giải phương trình trên để tìm \( x \):
\[ 2x + 12x - 15 = 6 \\ 14x = 21 \\ x = \frac{21}{14} = \frac{3}{2} \]Thay \( x = \frac{3}{2} \) vào phương trình \( y = 4x - 5 \) để tìm \( y \):
\[ y = 4\left(\frac{3}{2}\right) - 5 = 6 - 5 = 1 \]Vậy nghiệm của hệ là \( (x, y) = \left(\frac{3}{2}, 1\right) \).
-
Bài Tập 2: Giải hệ phương trình đối xứng
Giải hệ phương trình sau:
\[ \begin{cases} x^2 + y^2 = 10 \\ xy = 4 \end{cases} \]Giải:
Đặt \( S = x + y \) và \( P = xy = 4 \), ta có:
\[ S^2 = x^2 + 2xy + y^2 = 10 + 8 = 18 \\ S = \sqrt{18} = 3\sqrt{2} \quad \text{hoặc} \quad S = -3\sqrt{2} \]Do đó, phương trình bậc hai có hai nghiệm:
\[ t^2 - S t + P = 0 \\ t^2 - 3\sqrt{2}t + 4 = 0 \quad \text{hoặc} \quad t^2 + 3\sqrt{2}t + 4 = 0 \]Giải phương trình để tìm \( x \) và \( y \).
-
Bài Tập 3: Giải hệ phương trình chứa tham số
Giải hệ phương trình sau với tham số \( a \):
\[ \begin{cases} ax + y = 1 \\ x + ay = a \end{cases} \]Giải:
Trừ phương trình thứ hai cho phương trình thứ nhất:
\[ (a-1)x - (a-1)y = a - 1 \]Phân tích để tìm các giá trị của \( a \) và giải hệ phương trình.
XEM THÊM:
Bài Tập Vật Lý Về Động Lực Học
Động lực học là một phần quan trọng của vật lý, nghiên cứu về các lực và chuyển động của vật thể. Dưới đây là một số bài tập về động lực học kèm lời giải chi tiết.
-
Bài tập 1: Tính gia tốc của một vật
Một vật có khối lượng \( m = 10 \, \text{kg} \) được kéo trên mặt phẳng ngang với lực \( F = 50 \, \text{N} \). Lực ma sát tác dụng lên vật là \( f = 20 \, \text{N} \). Hãy tính gia tốc của vật.
Lời giải:
Gia tốc của vật được tính bằng công thức:
\[ a = \frac{F - f}{m} \]Thay số vào ta có:
\[ a = \frac{50 \, \text{N} - 20 \, \text{N}}{10 \, \text{kg}} = \frac{30 \, \text{N}}{10 \, \text{kg}} = 3 \, \text{m/s}^2 \]Vậy, gia tốc của vật là \( 3 \, \text{m/s}^2 \).
-
Bài tập 2: Tính lực kéo cần thiết
Một ô tô có khối lượng \( m = 1200 \, \text{kg} \) chuyển động với gia tốc \( a = 2 \, \text{m/s}^2 \). Hãy tính lực kéo cần thiết để ô tô đạt được gia tốc này.
Lời giải:
Lực kéo cần thiết được tính bằng công thức:
\[ F = m \cdot a \]Thay số vào ta có:
\[ F = 1200 \, \text{kg} \cdot 2 \, \text{m/s}^2 = 2400 \, \text{N} \]Vậy, lực kéo cần thiết là \( 2400 \, \text{N} \).
-
Bài tập 3: Định luật II Newton và bài toán lực
Một vật có khối lượng \( m = 5 \, \text{kg} \) chịu tác dụng của hai lực đồng thời: lực \( F_1 = 15 \, \text{N} \) hướng về phía đông và lực \( F_2 = 10 \, \text{N} \) hướng về phía bắc. Hãy xác định độ lớn và hướng của gia tốc.
Lời giải:
Độ lớn của lực tổng hợp \( F \) được tính bằng định lý Pythagore:
\[ F = \sqrt{F_1^2 + F_2^2} = \sqrt{15^2 + 10^2} = \sqrt{225 + 100} = \sqrt{325} \approx 18 \, \text{N} \]Gia tốc được tính bằng công thức:
\[ a = \frac{F}{m} = \frac{18 \, \text{N}}{5 \, \text{kg}} = 3.6 \, \text{m/s}^2 \]Góc giữa gia tốc và hướng đông được tính bằng:
\[ \theta = \arctan\left(\frac{F_2}{F_1}\right) = \arctan\left(\frac{10}{15}\right) \approx 33.69^\circ \]Vậy, gia tốc của vật có độ lớn \( 3.6 \, \text{m/s}^2 \) và hợp với hướng đông một góc \( 33.69^\circ \) về phía bắc.

Bài Tập Tiếng Anh Về Câu Điều Kiện
Câu điều kiện trong tiếng Anh là một phần ngữ pháp quan trọng, giúp diễn đạt các tình huống có thể xảy ra hoặc đã xảy ra. Dưới đây là một số bài tập về câu điều kiện kèm lời giải chi tiết.
-
Bài tập 1: Câu điều kiện loại 1
Viết lại các câu sau bằng cách sử dụng câu điều kiện loại 1:
- If it (rain), we (stay) at home.
- If she (study) hard, she (pass) the exam.
Lời giải:
- If it rains, we will stay at home.
- If she studies hard, she will pass the exam.
-
Bài tập 2: Câu điều kiện loại 2
Hoàn thành các câu sau bằng cách sử dụng câu điều kiện loại 2:
- If I (be) you, I (tell) him the truth.
- If they (have) enough money, they (buy) a new house.
Lời giải:
- If I were you, I would tell him the truth.
- If they had enough money, they would buy a new house.
-
Bài tập 3: Câu điều kiện loại 3
Chuyển đổi các câu sau thành câu điều kiện loại 3:
- If she (leave) earlier, she (catch) the bus.
- If they (work) harder, they (succeed) in the project.
Lời giải:
- If she had left earlier, she would have caught the bus.
- If they had worked harder, they would have succeeded in the project.
-
Bài tập 4: Kết hợp các loại câu điều kiện
Viết lại các câu sau bằng cách sử dụng sự kết hợp giữa các loại câu điều kiện:
- If he (not miss) the train, he (arrive) on time. (Loại 3 và loại 2)
- If she (study) more, she (get) better grades. (Loại 2 và loại 1)
Lời giải:
- If he hadn't missed the train, he would arrive on time.
- If she studied more, she will get better grades.

Bài Tập Toán Hình Học Không Gian
Hình học không gian là một phần quan trọng trong toán học, giúp chúng ta hiểu về các đối tượng ba chiều như hình lập phương, hình cầu, hình nón, và nhiều dạng khác. Dưới đây là một số bài tập về hình học không gian kèm lời giải chi tiết.
-
Bài tập 1: Tính thể tích hình lập phương
Một hình lập phương có cạnh \( a = 5 \, \text{cm} \). Hãy tính thể tích của hình lập phương này.
Lời giải:
Thể tích của hình lập phương được tính bằng công thức:
\[ V = a^3 \]Thay số vào ta có:
\[ V = 5^3 = 125 \, \text{cm}^3 \]Vậy, thể tích của hình lập phương là \( 125 \, \text{cm}^3 \).
-
Bài tập 2: Tính diện tích xung quanh của hình nón
Một hình nón có bán kính đáy \( r = 4 \, \text{cm} \) và đường sinh \( l = 7 \, \text{cm} \). Hãy tính diện tích xung quanh của hình nón này.
Lời giải:
Diện tích xung quanh của hình nón được tính bằng công thức:
\[ S_{xq} = \pi r l \]Thay số vào ta có:
\[ S_{xq} = \pi \times 4 \times 7 = 28\pi \, \text{cm}^2 \]Vậy, diện tích xung quanh của hình nón là \( 28\pi \, \text{cm}^2 \).
-
Bài tập 3: Tính thể tích khối cầu
Một khối cầu có bán kính \( r = 6 \, \text{cm} \). Hãy tính thể tích của khối cầu này.
Lời giải:
Thể tích của khối cầu được tính bằng công thức:
\[ V = \frac{4}{3} \pi r^3 \]Thay số vào ta có:
\[ V = \frac{4}{3} \pi \times 6^3 = \frac{4}{3} \pi \times 216 = 288\pi \, \text{cm}^3 \]Vậy, thể tích của khối cầu là \( 288\pi \, \text{cm}^3 \).
-
Bài tập 4: Tính diện tích toàn phần của hình trụ
Một hình trụ có bán kính đáy \( r = 3 \, \text{cm} \) và chiều cao \( h = 10 \, \text{cm} \). Hãy tính diện tích toàn phần của hình trụ này.
Lời giải:
Diện tích toàn phần của hình trụ được tính bằng công thức:
\[ S_{tp} = 2\pi r(h + r) \]Thay số vào ta có:
\[ S_{tp} = 2\pi \times 3 \times (10 + 3) = 6\pi \times 13 = 78\pi \, \text{cm}^2 \]Vậy, diện tích toàn phần của hình trụ là \( 78\pi \, \text{cm}^2 \).
Bài Tập Vật Lý Về Nhiệt Học
Dưới đây là một số bài tập về Nhiệt học giúp bạn ôn luyện và củng cố kiến thức.
-
Một lượng nước có khối lượng \( m = 2 \, \text{kg} \) được đun từ nhiệt độ ban đầu \( t_1 = 20^\circ C \) đến nhiệt độ \( t_2 = 100^\circ C \). Tính nhiệt lượng cần thiết để đun nóng lượng nước này. Biết nhiệt dung riêng của nước là \( c = 4200 \, \text{J/kg}^\circ C \).
Giải: Nhiệt lượng cần cung cấp được tính theo công thức:
\[ Q = mc(t_2 - t_1) \]Thay số vào công thức:
\[ Q = 2 \times 4200 \times (100 - 20) = 672,000 \, \text{J} \]Vậy nhiệt lượng cần thiết là 672 kJ.
-
Một thanh nhôm có khối lượng \( m = 0.5 \, \text{kg} \) được nung nóng từ nhiệt độ \( t_1 = 30^\circ C \) lên \( t_2 = 250^\circ C \). Tính nhiệt lượng mà thanh nhôm hấp thụ. Biết nhiệt dung riêng của nhôm là \( c = 880 \, \text{J/kg}^\circ C \).
Giải: Nhiệt lượng hấp thụ được tính theo công thức:
\[ Q = mc(t_2 - t_1) \]Thay số vào công thức:
\[ Q = 0.5 \times 880 \times (250 - 30) = 96,800 \, \text{J} \]Vậy nhiệt lượng hấp thụ là 96.8 kJ.
-
Một động cơ có công suất \( P = 500 \, \text{W} \) được sử dụng để truyền nhiệt cho một chất lỏng trong 10 phút. Nếu hiệu suất của động cơ là 30%, tính nhiệt lượng mà chất lỏng nhận được.
Giải: Công của động cơ trong thời gian 10 phút là:
\[ A = P \times t = 500 \times 600 = 300,000 \, \text{J} \]Nhiệt lượng mà chất lỏng nhận được:
\[ Q = \eta \times A = 0.3 \times 300,000 = 90,000 \, \text{J} \]Vậy chất lỏng nhận được 90 kJ nhiệt lượng.
Những bài tập trên đây tập trung vào các khái niệm cơ bản về nhiệt học như nhiệt lượng, nhiệt dung riêng và hiệu suất, giúp bạn nắm vững kiến thức để áp dụng vào các bài toán thực tế.

Bài Tập Tiếng Anh Về Các Loại Câu Hỏi
Dưới đây là một số bài tập giúp bạn làm quen và hiểu rõ hơn về các loại câu hỏi trong tiếng Anh, bao gồm câu hỏi Yes/No, câu hỏi Wh-, câu hỏi đuôi (tag questions), và câu hỏi lựa chọn (choice questions).
-
Câu hỏi Yes/No:
- Did you finish your homework?
- Are they coming to the party?
- Can she speak English fluently?
Bài tập: Chuyển các câu sau thành câu hỏi Yes/No:
- She is a doctor. (Is she a doctor?)
- They have a car. (Do they have a car?)
- He can play the guitar. (Can he play the guitar?)
-
Câu hỏi Wh-:
- What are you doing?
- Where do you live?
- Why did he leave early?
Bài tập: Hoàn thành các câu hỏi Wh- dưới đây:
- ________ is your favorite color? (What)
- ________ do you go to school? (Where)
- ________ did she come? (When)
-
Câu hỏi đuôi (Tag Questions):
- She is your friend, isn’t she?
- They don't like pizza, do they?
- He will come tomorrow, won't he?
Bài tập: Thêm câu hỏi đuôi vào các câu sau:
- You are a student, __________? (aren’t you)
- She can swim, __________? (can’t she)
- They didn’t go to the cinema, __________? (did they)
-
Câu hỏi lựa chọn (Choice Questions):
- Do you want tea or coffee?
- Is she coming with us or staying at home?
- Would you like to watch a movie or read a book?
Bài tập: Hoàn thành các câu hỏi lựa chọn dưới đây:
- Do you prefer cats __________ dogs? (or)
- Would you like to go out __________ stay in? (or)
- Is he taller __________ shorter than you? (or)
Những bài tập trên giúp bạn làm quen với các dạng câu hỏi phổ biến trong tiếng Anh. Hãy luyện tập thường xuyên để thành thạo các loại câu hỏi này.
Bài Tập Toán Về Tích Phân
Dưới đây là một số bài tập về tích phân giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán. Mỗi bài tập sẽ đi kèm với lời giải chi tiết để bạn có thể tự kiểm tra kết quả của mình.
-
Bài tập 1: Tính tích phân xác định của hàm số \( f(x) = x^2 \) trên đoạn \([1, 3]\).
Lời giải:
Ta có tích phân xác định:
\[ \int_{1}^{3} x^2 \, dx = \left[\frac{x^3}{3}\right]_{1}^{3} = \frac{3^3}{3} - \frac{1^3}{3} = \frac{27}{3} - \frac{1}{3} = \frac{26}{3} \] -
Bài tập 2: Tính tích phân xác định của hàm số \( f(x) = 2x + 1 \) trên đoạn \([-2, 2]\).
Lời giải:
Ta tính tích phân:
\[ \int_{-2}^{2} (2x + 1) \, dx = \left[x^2 + x\right]_{-2}^{2} = \left[(2^2 + 2) - ((-2)^2 + (-2))\right] = (4 + 2) - (4 - 2) = 6 - 2 = 4 \] -
Bài tập 3: Tính tích phân của hàm số \( f(x) = \sin(x) \) trên đoạn \([0, \pi]\).
Lời giải:
Ta có:
\[ \int_{0}^{\pi} \sin(x) \, dx = \left[-\cos(x)\right]_{0}^{\pi} = -\cos(\pi) + \cos(0) = -(-1) + 1 = 2 \] -
Bài tập 4: Tính tích phân của hàm số \( f(x) = e^x \) trên đoạn \([0, 1]\).
Lời giải:
Ta tính tích phân:
\[ \int_{0}^{1} e^x \, dx = \left[e^x\right]_{0}^{1} = e^1 - e^0 = e - 1 \] -
Bài tập 5: Tính tích phân xác định của hàm số \( f(x) = \frac{1}{x} \) trên đoạn \([1, 2]\).
Lời giải:
Ta có:
\[ \int_{1}^{2} \frac{1}{x} \, dx = \left[\ln |x|\right]_{1}^{2} = \ln(2) - \ln(1) = \ln(2) \]
Những bài tập trên giúp bạn nắm vững các khái niệm cơ bản về tích phân và cách áp dụng chúng vào việc giải các bài toán thực tế. Hãy luyện tập thường xuyên để nâng cao kỹ năng toán học của bạn.