Lịch Thi Đấu Bóng Đá Việt Nam Quốc Gia: Cập Nhật Đầy Đủ Mới Nhất 2024

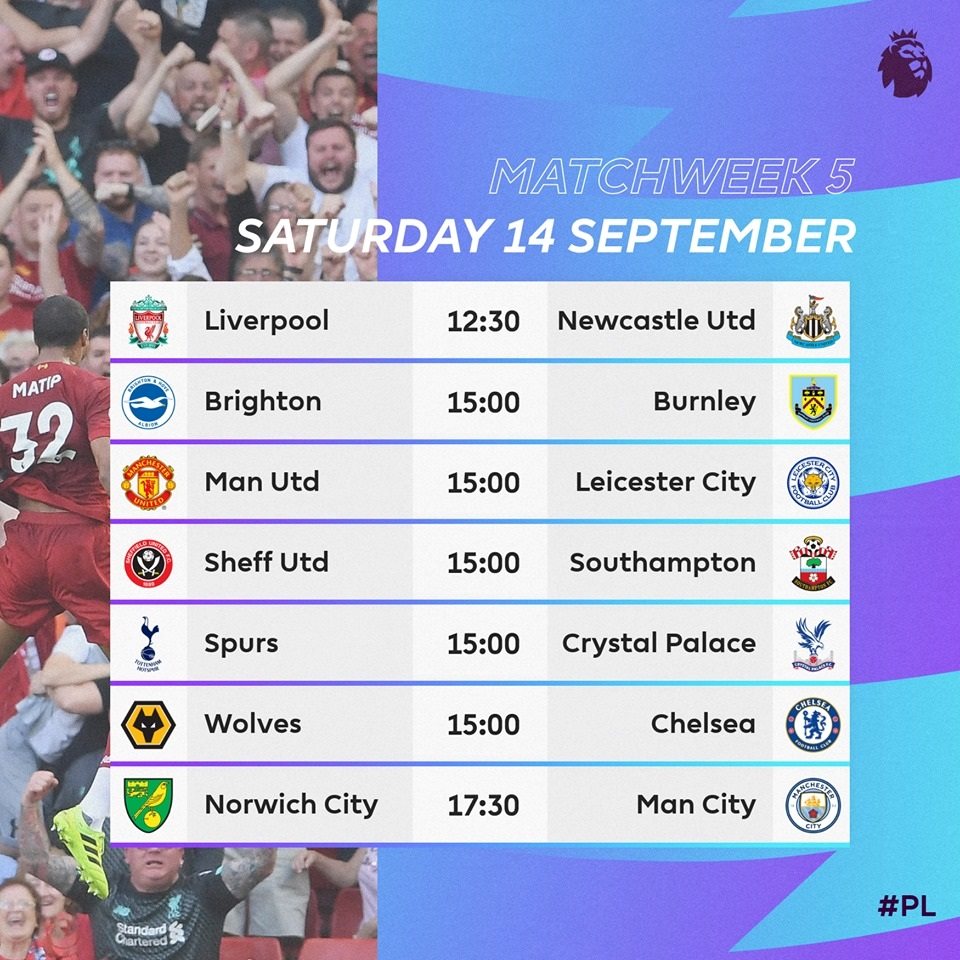
Lịch thi đấu bóng đá quốc gia Việt Nam bao gồm các giải đấu chính như V-League, Cúp Quốc Gia, và các trận đấu của đội tuyển quốc gia. Dưới đây là thông tin chi tiết về lịch thi đấu và những điểm đáng chú ý.

1. Lịch Thi Đấu V-League

• Giải V-League là giải đấu cao nhất của bóng đá Việt Nam, quy tụ các câu lạc bộ hàng đầu cả nước.
• Các vòng đấu diễn ra từ tháng 1 đến tháng 10 hàng năm, với sự tham gia của 14 đội bóng.
• Đặc biệt, vòng đấu cuối thường quyết định đội vô địch cũng như các suất thăng hạng, xuống hạng.

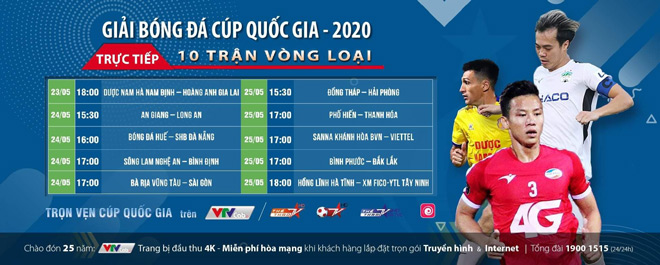
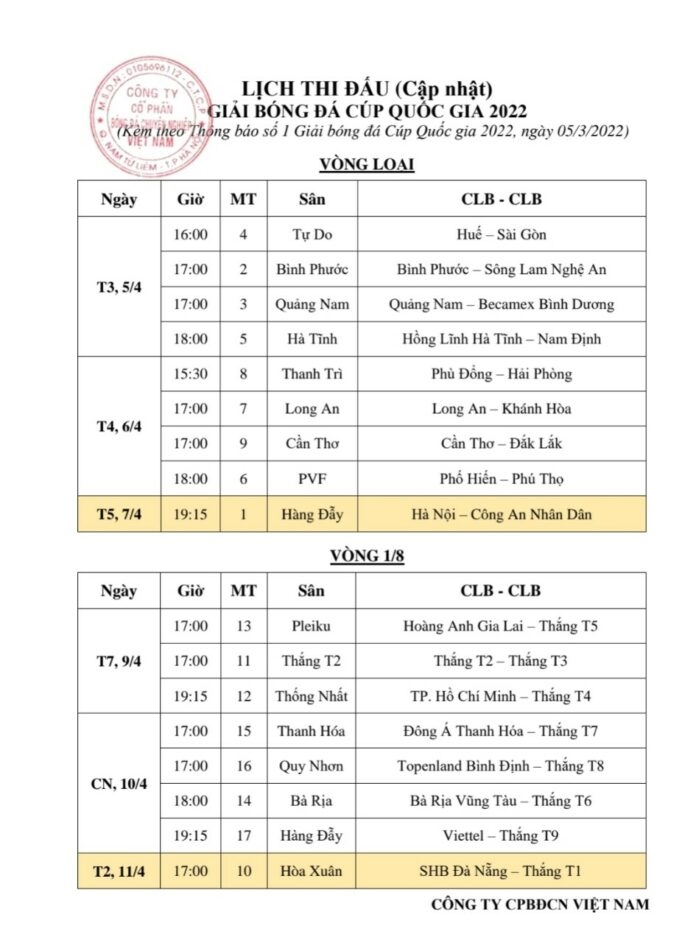
2. Lịch Thi Đấu Cúp Quốc Gia

• Cúp Quốc Gia là giải đấu loại trực tiếp, bắt đầu từ tháng 4 và kết thúc vào tháng 9 hàng năm.
• Các câu lạc bộ từ V-League và hạng Nhất đều có quyền tham gia, tạo nên những trận đấu hấp dẫn giữa các đội bóng từ các hạng đấu khác nhau.

3. Lịch Thi Đấu Đội Tuyển Quốc Gia

Đội tuyển quốc gia Việt Nam thi đấu các giải đấu quốc tế như AFF Cup, vòng loại World Cup, và các trận giao hữu quốc tế. Lịch thi đấu của đội tuyển thường được công bố sớm để người hâm mộ có thể theo dõi và cổ vũ.

• Giải đấu AFF Cup: Diễn ra hai năm một lần, thu hút sự chú ý lớn từ người hâm mộ.
• Vòng loại World Cup: Đội tuyển Việt Nam thi đấu với các đội bóng khác trong khu vực và châu Á.
• Giao hữu quốc tế: Các trận giao hữu được tổ chức để đội tuyển rèn luyện và thử nghiệm đội hình.

4. Các Điểm Nổi Bật Trong Lịch Thi Đấu

1. Trận derby giữa các đội bóng lớn như Hà Nội FC và Hoàng Anh Gia Lai luôn thu hút lượng khán giả đông đảo.
2. Các trận đấu quyết định tại V-League vào cuối mùa giải là những trận không thể bỏ lỡ.
3. Các trận đấu của đội tuyển quốc gia tại sân Mỹ Đình thường là điểm nhấn trong các chiến dịch vòng loại và AFF Cup.

5. Kết Luận

Lịch thi đấu bóng đá quốc gia Việt Nam luôn mang đến những trận cầu kịch tính và hấp dẫn. Người hâm mộ có thể dễ dàng theo dõi lịch thi đấu qua các kênh thông tin thể thao uy tín để không bỏ lỡ những trận đấu quan trọng của các đội bóng yêu thích.

Dưới đây là mục lục tổng hợp chi tiết về lịch thi đấu bóng đá quốc gia Việt Nam, bao gồm các giải đấu chính như V-League, Cúp Quốc Gia, và các trận đấu của đội tuyển quốc gia. Mục lục được thiết kế để giúp bạn dễ dàng tìm kiếm và theo dõi các trận đấu yêu thích.

1. Lịch Thi Đấu V-League 2024
   • Lịch trình từng vòng đấu của V-League 2024.
   • Những trận cầu đáng chú ý giữa các đội bóng hàng đầu.
   • Cập nhật thời gian, địa điểm thi đấu và kết quả chi tiết.
2. Lịch Thi Đấu Cúp Quốc Gia 2024
   • Thời gian và các vòng đấu từ vòng loại đến chung kết.
   • Danh sách các đội bóng tham gia và các cặp đấu quan trọng.
   • Phân tích cơ hội và dự đoán kết quả các trận đấu.
3. Lịch Thi Đấu Đội Tuyển Quốc Gia Việt Nam
   • Thông tin lịch thi đấu của đội tuyển tại các giải đấu quốc tế như AFF Cup và vòng loại World Cup.
   • Các trận giao hữu quốc tế và lịch thi đấu cụ thể.
   • Những trận đấu quyết định và đáng mong chờ nhất của đội tuyển.
4. Kết Quả Thi Đấu Bóng Đá Quốc Gia Việt Nam
   • Kết quả từng trận đấu tại V-League 2024.
   • Tổng hợp kết quả các trận đấu tại Cúp Quốc Gia.
   • Phân tích chuyên sâu kết quả các trận đấu của đội tuyển quốc gia.
5. Bảng Xếp Hạng Bóng Đá Quốc Gia Việt Nam
   • Bảng xếp hạng V-League 2024 cập nhật sau mỗi vòng đấu.
   • Xếp hạng các đội bóng tại Cúp Quốc Gia.
   • Vị trí đội tuyển quốc gia Việt Nam trên bảng xếp hạng FIFA.
6. Tin Tức Nổi Bật Trong Bóng Đá Việt Nam
   • Chuyển nhượng cầu thủ và các tin tức nóng hổi.
   • Những câu chuyện bên lề thú vị về các đội bóng.
   • Tin tức về các cầu thủ chấn thương và sự trở lại sân cỏ.

Dưới đây là các dạng bài tập toán học phổ biến, mỗi bài có lời giải chi tiết. Các bài tập này được thiết kế để giúp bạn nắm vững kiến thức từ cơ bản đến nâng cao, phù hợp cho học sinh và sinh viên đang ôn luyện môn Toán.

1. Bài Tập 1: Phương Trình Bậc Hai

   Giải phương trình bậc hai dạng tổng quát: \[ ax^2 + bx + c = 0 \]

   • Xác định các hệ số \(a\), \(b\), \(c\).
   • Sử dụng công thức nghiệm: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
   • Phân tích kết quả và nghiệm của phương trình.
2. Bài Tập 2: Hệ Phương Trình Tuyến Tính

   Giải hệ phương trình hai ẩn:

   • \[ \begin{cases} ax + by = c \\ dx + ey = f \end{cases} \]
   • Sử dụng phương pháp thế hoặc cộng đại số.
   • Tìm nghiệm của hệ phương trình.
3. Bài Tập 3: Tích Phân Cơ Bản

   Tính tích phân:

   • \[ \int (x^2 + 3x + 2) \, dx \]
   • Sử dụng các công thức tích phân cơ bản.
   • Kết quả: \(\frac{x^3}{3} + \frac{3x^2}{2} + 2x + C\).
4. Bài Tập 4: Đạo Hàm Hàm Số Lượng Giác

   Tính đạo hàm của hàm số:

   • \[ y = \sin(x) + \cos(x) \]
   • Sử dụng công thức đạo hàm: \(\frac{d}{dx}\sin(x) = \cos(x)\) và \(\frac{d}{dx}\cos(x) = -\sin(x)\).
   • Kết quả: \[ y' = \cos(x) - \sin(x) \]
5. Bài Tập 5: Số Phức và Biểu Diễn Hình Học

   Biểu diễn số phức trên mặt phẳng tọa độ:

   • Số phức: \(z = a + bi\).
   • Biểu diễn trên mặt phẳng phức với trục thực và trục ảo.
   • Khoảng cách đến gốc tọa độ: \(\left| z \right| = \sqrt{a^2 + b^2}\).
6. Bài Tập 6: Bất Đẳng Thức Cauchy-Schwarz

   Chứng minh bất đẳng thức Cauchy-Schwarz:

   • \[ (a^2 + b^2)(x^2 + y^2) \geq (ax + by)^2 \]
   • Áp dụng cho các bài toán thực tế để tìm giá trị cực tiểu hoặc cực đại.
7. Bài Tập 7: Hình Học Không Gian

   Tính thể tích khối chóp:

   • Khối chóp có đáy là hình vuông và chiều cao \(h\).
   • Công thức tính thể tích: \[ V = \frac{1}{3} S \cdot h \]
8. Bài Tập 8: Dãy Số và Giới Hạn

   Tìm giới hạn của dãy số:

   • Dãy số: \[ a_n = \frac{1}{n} \]
   • Kết quả: \[ \lim_{n \to \infty} a_n = 0 \]
9. Bài Tập 9: Xác Suất Cơ Bản

   Tính xác suất của một biến cố:

   • Xác suất xuất hiện mặt ngửa khi tung một đồng xu.
   • Kết quả: \[ P = \frac{1}{2} \]
10. Bài Tập 10: Lý Thuyết Đồ Thị Cơ Bản

    Vẽ đồ thị và tìm đường đi ngắn nhất:

    • Đồ thị với các đỉnh và cạnh.
    • Sử dụng thuật toán Dijkstra để tìm đường đi ngắn nhất.

Phương trình bậc hai là một trong những dạng bài tập quan trọng trong chương trình toán học. Bài toán yêu cầu tìm nghiệm của phương trình bậc hai dạng tổng quát:

Trong đó:

• \(a\), \(b\), \(c\) là các hệ số đã biết, \(a \neq 0\).
• \(x\) là ẩn số cần tìm.

Hướng dẫn giải:

1. Bước 1: Xác định các hệ số \(a\), \(b\), và \(c\) từ phương trình đã cho.
2. Bước 2: Tính biệt thức \(\Delta\) theo công thức: \[ \Delta = b^2 - 4ac \]
3. Bước 3: Xét dấu của \(\Delta\) để tìm nghiệm:
   • Nếu \(\Delta > 0\), phương trình có hai nghiệm phân biệt: \[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
   • Nếu \(\Delta = 0\), phương trình có nghiệm kép: \[ x = \frac{-b}{2a} \]
   • Nếu \(\Delta < 0\), phương trình vô nghiệm (không có nghiệm thực).
4. Bước 4: Viết kết quả nghiệm của phương trình.

Ví dụ:

Giải phương trình sau:

• Bước 1: Xác định hệ số: \(a = 2\), \(b = -4\), \(c = 2\).
• Bước 2: Tính biệt thức: \[ \Delta = (-4)^2 - 4 \cdot 2 \cdot 2 = 16 - 16 = 0 \]
• Bước 3: Vì \(\Delta = 0\), phương trình có nghiệm kép: \[ x = \frac{-(-4)}{2 \cdot 2} = \frac{4}{4} = 1 \]

Kết quả: Phương trình có nghiệm kép \(x = 1\).

Hệ phương trình tuyến tính là dạng bài tập cơ bản và quan trọng trong toán học, thường được sử dụng để giải các bài toán liên quan đến nhiều ẩn số. Dưới đây là hướng dẫn chi tiết về cách giải một hệ phương trình tuyến tính hai ẩn:

Trong đó:

• \(a\), \(b\), \(c\), \(d\), \(e\), \(f\) là các hệ số đã biết.
• \(x\) và \(y\) là các ẩn số cần tìm.

Hướng dẫn giải:

1. Bước 1: Chọn một trong hai phương pháp giải: phương pháp thế hoặc phương pháp cộng đại số.
2. Bước 2: Nếu sử dụng phương pháp thế:
   • Giải một phương trình theo một ẩn (ví dụ, từ phương trình thứ nhất tìm \(x\) theo \(y\)).
   • Thế giá trị của ẩn đó vào phương trình còn lại để tìm ra ẩn còn lại.
3. Bước 3: Nếu sử dụng phương pháp cộng đại số:
   • Nhân một hoặc cả hai phương trình với một số sao cho hệ số của một trong hai ẩn trở thành đối nhau.
   • Cộng hai phương trình để khử đi một ẩn, sau đó giải phương trình còn lại để tìm ẩn thứ nhất.
   • Thế giá trị ẩn vừa tìm được vào một trong hai phương trình ban đầu để tìm ra ẩn còn lại.
4. Bước 4: Viết kết quả nghiệm của hệ phương trình.

Ví dụ:

Giải hệ phương trình sau:

• Bước 1: Chọn phương pháp thế. Từ phương trình thứ hai, ta có: \[ x = y + 1 \]
• Bước 2: Thế giá trị \(x = y + 1\) vào phương trình thứ nhất: \[ 2(y + 1) + 3y = 6 \]
  • Giải phương trình: \[ 2y + 2 + 3y = 6 \implies 5y = 4 \implies y = \frac{4}{5} \]
• Bước 3: Thế giá trị \(y = \frac{4}{5}\) vào \(x = y + 1\): \[ x = \frac{4}{5} + 1 = \frac{9}{5} \]

Kết quả: Hệ phương trình có nghiệm \(x = \frac{9}{5}\), \(y = \frac{4}{5}\).

Tích phân là một trong những khái niệm cơ bản và quan trọng trong giải tích, thường được sử dụng để tính diện tích, thể tích, và nhiều ứng dụng khác trong toán học. Dưới đây là hướng dẫn chi tiết về cách giải một bài toán tích phân cơ bản:

Yêu cầu: Tính tích phân của hàm số \(f(x)\) trên đoạn \([a, b]\).

Trong đó:

• \(f(x)\) là hàm số cần lấy tích phân.
• \(a\) và \(b\) là cận dưới và cận trên của tích phân.

Hướng dẫn giải:

1. Bước 1: Tìm nguyên hàm của hàm số \(f(x)\), ký hiệu là \(F(x)\), sao cho \(F'(x) = f(x)\).
2. Bước 2: Tính giá trị của \(F(x)\) tại hai cận \(a\) và \(b\), tức là \(F(b)\) và \(F(a)\).
3. Bước 3: Tính giá trị tích phân bằng cách trừ hai giá trị này: \[ \int_{a}^{b} f(x) \, dx = F(b) - F(a) \]

Ví dụ:

Giải bài toán sau:

Tính tích phân của hàm số \(f(x) = 2x\) trên đoạn \([1, 3]\).

• Bước 1: Tìm nguyên hàm của \(f(x) = 2x\): \[ F(x) = x^2 \]
• Bước 2: Tính giá trị của \(F(x)\) tại cận trên \(b = 3\) và cận dưới \(a = 1\): \[ F(3) = 3^2 = 9, \quad F(1) = 1^2 = 1 \]
• Bước 3: Tính tích phân: \[ \int_{1}^{3} 2x \, dx = 9 - 1 = 8 \]

Kết quả: Giá trị của tích phân là \(8\).

Trong phần này, chúng ta sẽ đi sâu vào việc tính đạo hàm của các hàm số lượng giác cơ bản. Đạo hàm của các hàm số lượng giác là một phần quan trọng trong toán học cao cấp và có ứng dụng trong nhiều lĩnh vực như vật lý và kỹ thuật. Dưới đây là các công thức đạo hàm cơ bản và các bài tập áp dụng.

Công Thức Đạo Hàm Hàm Số Lượng Giác Cơ Bản

• \[\frac{d}{dx}(\sin x) = \cos x\]
• \[\frac{d}{dx}(\cos x) = -\sin x\]
• \[\frac{d}{dx}(\tan x) = \sec^2 x\]
• \[\frac{d}{dx}(\cot x) = -\csc^2 x\]
• \[\frac{d}{dx}(\sec x) = \sec x \cdot \tan x\]
• \[\frac{d}{dx}(\csc x) = -\csc x \cdot \cot x\]

Bài Tập Ứng Dụng

Bài Tập 1: Tính đạo hàm của hàm số \(f(x) = \sin(x) + \cos(x)\).

1. Áp dụng công thức đạo hàm: \[f'(x) = \frac{d}{dx}(\sin x) + \frac{d}{dx}(\cos x)\].
2. Sử dụng công thức đạo hàm cơ bản: \[f'(x) = \cos x - \sin x\].
3. Kết quả: Đạo hàm của hàm số là \[f'(x) = \cos x - \sin x\].

Bài Tập 2: Tính đạo hàm của hàm số \(g(x) = \tan(x) - \sec(x)\).

1. Áp dụng công thức đạo hàm: \[g'(x) = \frac{d}{dx}(\tan x) - \frac{d}{dx}(\sec x)\].
2. Sử dụng công thức đạo hàm cơ bản: \[g'(x) = \sec^2 x - \sec x \cdot \tan x\].
3. Kết quả: Đạo hàm của hàm số là \[g'(x) = \sec^2 x - \sec x \cdot \tan x\].

Bài Tập 3: Tính đạo hàm của hàm số \(h(x) = \csc(x) + \cot(x)\).

1. Áp dụng công thức đạo hàm: \[h'(x) = \frac{d}{dx}(\csc x) + \frac{d}{dx}(\cot x)\].
2. Sử dụng công thức đạo hàm cơ bản: \[h'(x) = -\csc x \cdot \cot x - \csc^2 x\].
3. Kết quả: Đạo hàm của hàm số là \[h'(x) = -\csc x \cdot \cot x - \csc^2 x\].

Hãy thực hành các bài tập trên để làm quen với việc tính đạo hàm của các hàm số lượng giác. Nếu gặp khó khăn, hãy tham khảo lại các công thức cơ bản hoặc tìm kiếm thêm tài liệu để hiểu rõ hơn.

Số phức là một khái niệm cơ bản trong toán học, đại diện cho số có dạng \( z = a + bi \), trong đó \( a \) và \( b \) là các số thực, và \( i \) là đơn vị ảo với \( i^2 = -1 \).

Dưới đây là một số bước chi tiết để hiểu và biểu diễn hình học số phức:

1. Phần thực và phần ảo của số phức:

   Số phức \( z = a + bi \) có phần thực là \( a \) và phần ảo là \( b \).

   Ví dụ: Với số phức \( z = 3 + 4i \), phần thực là \( 3 \) và phần ảo là \( 4 \).

2. Biểu diễn số phức trên mặt phẳng phức:

   Mỗi số phức có thể được biểu diễn như một điểm trên mặt phẳng phức, với trục hoành là phần thực và trục tung là phần ảo.

   Điểm tương ứng với số phức \( z = a + bi \) trên mặt phẳng sẽ có tọa độ \( (a, b) \).

3. Độ lớn (modul) của số phức:

   Độ lớn của số phức \( z = a + bi \) được tính bằng công thức:

   \[ |z| = \sqrt{a^2 + b^2} \]

   Ví dụ: Độ lớn của số phức \( z = 3 + 4i \) là:

   \[ |z| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \]

4. Góc (arg) của số phức:

   Góc của số phức \( z = a + bi \) với trục thực dương được gọi là góc \( \theta \), được tính bằng công thức:

   \[ \theta = \text{tan}^{-1}\left(\frac{b}{a}\right) \]

   Ví dụ: Với số phức \( z = 1 + i \), góc sẽ là:

   \[ \theta = \text{tan}^{-1}\left(\frac{1}{1}\right) = 45^\circ \]

5. Biểu diễn hình học của số phức dưới dạng cực:

   Số phức \( z = a + bi \) có thể biểu diễn dưới dạng cực:

   \[ z = |z| \left(\cos \theta + i \sin \theta\right) \]

   Đây là cách biểu diễn số phức bằng độ lớn và góc.

Hy vọng các ví dụ và bước hướng dẫn trên giúp bạn hiểu rõ hơn về số phức và cách biểu diễn chúng trên mặt phẳng phức. Bài tập này yêu cầu học sinh nắm vững các khái niệm cơ bản và áp dụng chúng vào thực tế toán học.

Bất đẳng thức Cauchy-Schwarz là một trong những bất đẳng thức quan trọng trong toán học, đặc biệt hữu ích trong các bài toán liên quan đến đại số và giải tích. Bài tập này sẽ giúp bạn hiểu rõ hơn về bất đẳng thức này và cách áp dụng nó trong các bài toán cụ thể.

Bất Đẳng Thức Cauchy-Schwarz

Bất đẳng thức Cauchy-Schwarz trong không gian Euclid có dạng:

Trong đó, \(a_i\) và \(b_i\) là các phần tử thực của hai dãy số.

Bài Tập Ứng Dụng

Dưới đây là một số bài tập để thực hành việc áp dụng bất đẳng thức Cauchy-Schwarz.

1. Chứng minh rằng với mọi số thực \(x\) và \(y\), bất đẳng thức sau đây luôn đúng: \[ (x^2 + y^2)(1 + 1) \geq (x + y)^2 \]
2. Áp dụng bất đẳng thức Cauchy-Schwarz để chứng minh rằng: \[ (a^2 + b^2 + c^2)(x^2 + y^2 + z^2) \geq (ax + by + cz)^2 \]
3. Tìm giá trị nhỏ nhất của biểu thức sau: \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} \] khi biết \(x, y, z\) là các số thực và \(a, b, c\) là các hằng số dương.

Hướng Dẫn Giải

• Để giải bài 1, hãy sử dụng bất đẳng thức Cauchy-Schwarz với hai dãy số \([x, y]\) và \([1, 1]\).
• Trong bài 2, bạn có thể áp dụng bất đẳng thức Cauchy-Schwarz trong không gian ba chiều với các vector \([a, b, c]\) và \([x, y, z]\).
• Bài 3 yêu cầu bạn sử dụng các công cụ của bất đẳng thức Cauchy-Schwarz để tìm giá trị nhỏ nhất, hãy thử áp dụng biến đổi để đưa biểu thức về dạng phù hợp.

Bằng việc thực hành các bài tập trên, bạn sẽ nắm vững cách sử dụng bất đẳng thức Cauchy-Schwarz trong các tình huống khác nhau, từ đó tăng cường kỹ năng giải toán của mình.

Trong bài tập này, chúng ta sẽ khám phá các khái niệm cơ bản và ứng dụng của hình học không gian. Đây là một phần quan trọng trong chương trình toán học, giúp học sinh hiểu rõ hơn về các đối tượng ba chiều và cách tính toán các thông số liên quan.

1. Khối Đa Diện

Khối đa diện là một đối tượng hình học được bao bọc bởi các đa giác. Ví dụ, hình lập phương là một khối đa diện có sáu mặt là các hình vuông. Các khối đa diện thường gặp bao gồm:

• Hình lập phương
• Hình hộp chữ nhật
• Hình chóp
• Hình lăng trụ

2. Công Thức Tính Diện Tích và Thể Tích

Để tính toán diện tích và thể tích của các khối đa diện, ta cần áp dụng các công thức sau:

• Diện tích xung quanh của hình lăng trụ: \[ S_{xq} = P_{đáy} \times h \]
• Diện tích toàn phần của hình chóp: \[ S_{tp} = S_{xq} + S_{đáy} \]
• Thể tích của khối lập phương: \[ V = a^3 \]
• Thể tích của hình chóp: \[ V = \frac{1}{3} \times S_{đáy} \times h \]

3. Bài Tập Thực Hành

1. Tính diện tích toàn phần và thể tích của một hình lăng trụ đứng có đáy là hình vuông cạnh 5cm và chiều cao 10cm.
2. Tính thể tích của một hình chóp tam giác đều có cạnh đáy là 6cm và chiều cao là 8cm.
3. Cho một khối lập phương có cạnh 4cm. Tính diện tích toàn phần và thể tích của khối lập phương này.

4. Ứng Dụng Thực Tế

Hình học không gian không chỉ là một phần của chương trình học, mà còn có rất nhiều ứng dụng trong đời sống thực tế. Ví dụ, khi xây dựng các công trình kiến trúc, chúng ta cần tính toán chính xác diện tích và thể tích của các khối để đảm bảo tính khả thi và hiệu quả của công trình.

Việc hiểu rõ các nguyên tắc hình học không gian sẽ giúp bạn dễ dàng áp dụng trong các bài toán thực tế và trong công việc tương lai của mình.

Trong toán học, dãy số là một khái niệm cơ bản để nghiên cứu sự liên tục và tính chất của các dãy số trong trường số thực. Giới hạn của dãy số giúp xác định hành vi của dãy khi nó tiến dần đến vô cùng.

1. Khái niệm dãy số

Một dãy số là một tập hợp các số được sắp xếp theo một thứ tự nhất định. Thường thì các số trong dãy được biểu diễn dưới dạng \(a_1, a_2, a_3, \dots\).

2. Giới hạn của dãy số

Giới hạn của một dãy số là giá trị mà dãy số tiến dần tới khi số thứ tự của nó tăng lên vô hạn.

Cụ thể, nếu dãy số \(\{a_n\}\) có giới hạn là \(L\), khi đó:

\[
\lim_{{n \to \infty}} a_n = L
\]

3. Ví dụ minh họa

1. Dãy số đơn giản: Xét dãy số \(a_n = \frac{1}{n}\). Khi \(n\) tăng lên, \(a_n\) tiến dần về 0. Vì vậy:

   \[
   \lim_{{n \to \infty}} \frac{1}{n} = 0
   \]

2. Dãy số khác: Xét dãy số \(b_n = 2 + \frac{1}{n}\). Khi \(n\) tăng lên, \(b_n\) tiến dần về 2. Do đó:

   \[
   \lim_{{n \to \infty}} \left(2 + \frac{1}{n}\right) = 2
   \]

4. Bài tập thực hành

1. Chứng minh rằng dãy số \(c_n = \frac{n}{n+1}\) có giới hạn là 1.
2. Xác định giới hạn của dãy số \(d_n = \frac{2n^2 + 3}{n^2 + 1}\).
3. Giải quyết bài toán về dãy số Fibonacci và xác định xu hướng của nó khi \(n\) tiến đến vô cùng.

5. Lời kết

Việc nắm vững khái niệm và phương pháp xác định giới hạn của dãy số là cực kỳ quan trọng trong toán học. Điều này không chỉ giúp bạn hiểu sâu hơn về tính chất của các dãy số mà còn hỗ trợ rất nhiều trong việc giải quyết các bài toán phức tạp hơn liên quan đến hàm số và tích phân.

Xác suất là một khái niệm quan trọng trong toán học và thực tế. Để hiểu rõ hơn về xác suất, chúng ta sẽ cùng giải quyết các bài tập cơ bản dưới đây.

1. Xác suất của một sự kiện

Giả sử chúng ta có một sự kiện \( A \) xảy ra với xác suất \( P(A) \). Công thức tính xác suất là:

\[ P(A) = \frac{\text{số trường hợp thuận lợi}}{\text{tổng số trường hợp có thể xảy ra}} \]

Ví dụ: Nếu bạn tung một con xúc xắc, xác suất để ra mặt số 4 là:

\[ P(\text{ra số 4}) = \frac{1}{6} \]

2. Xác suất của nhiều sự kiện

Nếu hai sự kiện \( A \) và \( B \) độc lập nhau, xác suất của cả hai sự kiện cùng xảy ra là:

\[ P(A \cap B) = P(A) \times P(B) \]

Ví dụ: Nếu bạn tung hai con xúc xắc, xác suất để cả hai con đều ra mặt số 4 là:

\[ P(\text{cả hai ra số 4}) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} \]

3. Bài Tập Thực Hành

1. Trong một hộp có 5 viên bi đỏ và 3 viên bi xanh, lấy ngẫu nhiên 1 viên. Tính xác suất để lấy được viên bi đỏ.
2. Khi tung một đồng xu hai lần, xác suất để mặt ngửa xuất hiện cả hai lần là bao nhiêu?
3. Một bộ bài 52 lá, rút ngẫu nhiên 1 lá. Tính xác suất để rút được một lá át cơ.

4. Đáp án và Giải Thích

• Bài 1: Xác suất để lấy được viên bi đỏ là \[ P(\text{bi đỏ}) = \frac{5}{8} \].
• Bài 2: Xác suất để mặt ngửa xuất hiện cả hai lần là \[ P(\text{2 lần ngửa}) = \frac{1}{4} \].
• Bài 3: Xác suất để rút được lá át cơ là \[ P(\text{át cơ}) = \frac{1}{52} \].

Hy vọng rằng qua các bài tập này, bạn sẽ nắm vững hơn về lý thuyết xác suất và cách áp dụng nó trong thực tế.

Trong bài tập này, chúng ta sẽ tìm hiểu về lý thuyết đồ thị - một nhánh quan trọng trong toán học và tin học.

I. Khái niệm cơ bản

• Đồ thị: Là một cấu trúc bao gồm tập hợp các đỉnh (vertices) và các cạnh (edges) nối giữa các cặp đỉnh.
• Đỉnh (Vertex): Là các điểm nút trong đồ thị, ký hiệu là \( V \).
• Cạnh (Edge): Là đường nối giữa hai đỉnh, ký hiệu là \( E \).
• Bậc của đỉnh: Số cạnh kết nối với một đỉnh, ký hiệu là \( deg(v) \).

II. Các loại đồ thị

• Đồ thị vô hướng: Các cạnh không có hướng.
• Đồ thị có hướng: Các cạnh có hướng, nghĩa là có sự phân biệt điểm đầu và điểm cuối của cạnh.
• Đồ thị liên thông: Tồn tại ít nhất một đường đi giữa mọi cặp đỉnh.
• Đồ thị phân đôi: Đồ thị có thể chia tập đỉnh thành hai tập con sao cho các cạnh chỉ nối giữa hai tập con.

III. Một số định lý và tính chất

• Định lý Euler: Đối với đồ thị liên thông không có chu trình lẻ, số đỉnh có bậc lẻ luôn là số chẵn.
• Định lý về số cạnh: Trong một đồ thị có \( n \) đỉnh và \( m \) cạnh, tổng bậc của tất cả các đỉnh bằng \( 2m \).
• Chu trình Hamilton: Là chu trình đi qua mỗi đỉnh đúng một lần.

IV. Bài tập áp dụng

1. Cho đồ thị \( G = (V, E) \) với \( V = \{1, 2, 3, 4\} \) và \( E = \{(1, 2), (2, 3), (3, 4), (4, 1)\} \). Hãy vẽ đồ thị và xác định các tính chất của đồ thị này.
2. Xác định bậc của các đỉnh trong đồ thị vô hướng với 5 đỉnh và 7 cạnh.
3. Chứng minh rằng trong bất kỳ đồ thị đơn nào, số đỉnh có bậc lẻ luôn là số chẵn.

Hãy chắc chắn bạn nắm vững các khái niệm cơ bản trước khi chuyển sang các bài tập phức tạp hơn trong lý thuyết đồ thị. Lý thuyết đồ thị là nền tảng cho nhiều ứng dụng trong tin học và khoa học máy tính, bao gồm cả thuật toán tìm kiếm đường đi và tối ưu hóa mạng lưới.