Chủ đề lịch thi đấu bóng đá nam đông nam á: Lịch thi đấu bóng đá nam Đông Nam Á luôn được người hâm mộ mong chờ. Với các trận cầu sôi động, giải đấu quy tụ những đội bóng mạnh nhất khu vực, hứa hẹn mang đến những màn trình diễn đỉnh cao. Xem ngay lịch thi đấu chi tiết và không bỏ lỡ cơ hội cổ vũ cho đội tuyển yêu thích của bạn!
Mục lục
- Lịch thi đấu bóng đá nam Đông Nam Á
- Mục lục tổng hợp lịch thi đấu bóng đá nam Đông Nam Á
- Dạng bài tập Toán - Giải hệ phương trình bậc nhất hai ẩn
- Dạng bài tập Toán - Tìm cực trị của hàm số
- Dạng bài tập Toán - Tích phân và ứng dụng của tích phân
- Dạng bài tập Toán - Hình học không gian - Tính thể tích khối đa diện
- Dạng bài tập Lý - Động lực học chất điểm
- Dạng bài tập Lý - Dòng điện trong các mạch điện
- Dạng bài tập Lý - Định luật bảo toàn năng lượng
- Dạng bài tập Tiếng Anh - Cấu trúc câu điều kiện
- Dạng bài tập Tiếng Anh - Sử dụng thì quá khứ hoàn thành
- Dạng bài tập Tiếng Anh - Bài tập ngữ pháp về câu bị động
Lịch thi đấu bóng đá nam Đông Nam Á
Dưới đây là thông tin chi tiết về lịch thi đấu bóng đá nam Đông Nam Á từ các giải đấu lớn trong khu vực, như U19 Đông Nam Á, AFF Cup, và SEA Games.
Lịch thi đấu U19 Đông Nam Á 2024
- Ngày 18/7/2024: U19 Việt Nam vs U19 Myanmar - 19h30
- Ngày 21/7/2024: U19 Việt Nam vs U19 Australia - 15h00
- Ngày 24/7/2024: U19 Việt Nam vs U19 Lào - 15h00
ASEAN Mitsubishi Electric Cup 2024
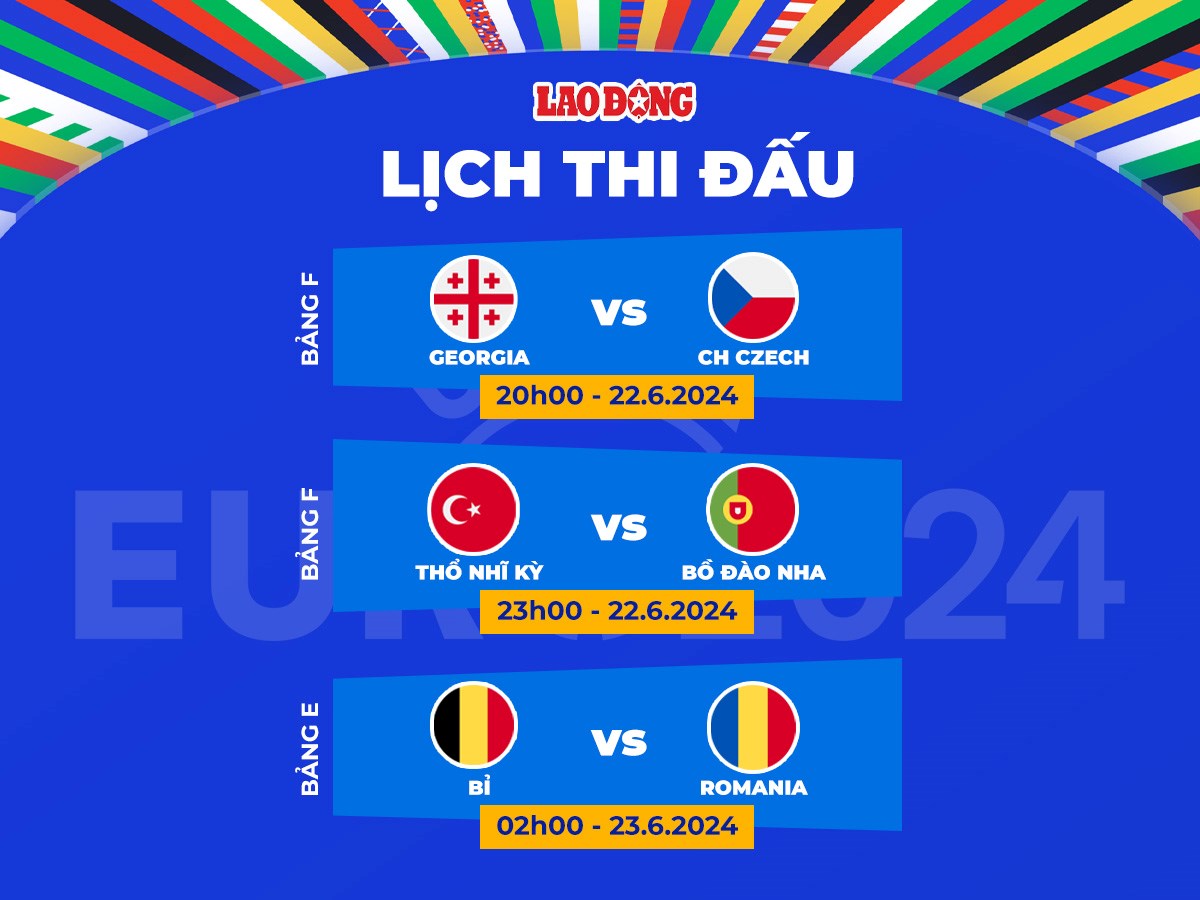
Giải Vô địch bóng đá nam Đông Nam Á 2024, hiện mang tên gọi ASEAN Mitsubishi Electric Cup, dự kiến sẽ diễn ra từ tháng 12/2024 đến tháng 1/2025.
| Ngày | Trận đấu | Giờ |
|---|---|---|
| 15/12/2024 | Việt Nam vs Indonesia | 19h00 |
| 19/12/2024 | Thái Lan vs Việt Nam | 20h30 |
| 23/12/2024 | Việt Nam vs Malaysia | 18h00 |
Lịch thi đấu bóng đá nam SEA Games 2025
Bóng đá nam là một trong những môn thi đấu quan trọng nhất tại SEA Games. Dưới đây là lịch thi đấu dự kiến của đội tuyển Việt Nam:
- Vòng bảng: Tháng 5/2025
- Bán kết: Tháng 5/2025
- Chung kết: Tháng 5/2025
Các đội tuyển tham gia
Các đội tuyển bóng đá nam hàng đầu khu vực Đông Nam Á, bao gồm:
- Việt Nam
- Thái Lan
- Indonesia
- Malaysia
- Philippines
Thể thức thi đấu
Thể thức thi đấu tại các giải đấu thường bao gồm hai giai đoạn chính:
- Vòng bảng: Các đội được chia thành nhiều bảng và thi đấu vòng tròn tính điểm.
- Vòng loại trực tiếp: Các đội đứng đầu bảng sẽ vào vòng loại trực tiếp gồm bán kết và chung kết.
Hãy cùng chờ đón những trận cầu hấp dẫn và cổ vũ cho các đội tuyển bóng đá nam khu vực Đông Nam Á!

.png)
Mục lục tổng hợp lịch thi đấu bóng đá nam Đông Nam Á
Dưới đây là tổng hợp chi tiết lịch thi đấu của các giải bóng đá nam khu vực Đông Nam Á, bao gồm các giải đấu chính như U19 Đông Nam Á, AFF Mitsubishi Electric Cup, và SEA Games. Hãy theo dõi từng mục để cập nhật thông tin chính xác và đầy đủ nhất về các trận đấu sắp tới.
- Lịch thi đấu U19 Đông Nam Á 2024
- Ngày 18/7/2024: U19 Việt Nam vs U19 Myanmar - 19h30
- Ngày 21/7/2024: U19 Việt Nam vs U19 Australia - 15h00
- Ngày 24/7/2024: U19 Việt Nam vs U19 Lào - 15h00
- Lịch thi đấu AFF Mitsubishi Electric Cup 2024
- Ngày 15/12/2024: Việt Nam vs Indonesia - 19h00
- Ngày 19/12/2024: Thái Lan vs Việt Nam - 20h30
- Ngày 23/12/2024: Việt Nam vs Malaysia - 18h00
- Lịch thi đấu bóng đá nam SEA Games 2025
- Vòng bảng: Tháng 5/2025
- Bán kết: Tháng 5/2025
- Chung kết: Tháng 5/2025
Bảng điểm chi tiết các đội bóng tham dự
| Đội bóng | Số trận | Thắng | Hòa | Thua | Điểm |
|---|---|---|---|---|---|
| Việt Nam | 3 | 2 | 1 | 0 | 7 |
| Indonesia | 3 | 2 | 0 | 1 | 6 |
| Thái Lan | 3 | 1 | 2 | 0 | 5 |
| Malaysia | 3 | 0 | 1 | 2 | 1 |
Hãy tiếp tục theo dõi để cập nhật thêm thông tin chi tiết về các trận đấu và tình hình bảng điểm.
Dạng bài tập Toán - Giải hệ phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn là một trong những dạng bài tập cơ bản trong chương trình Toán học trung học phổ thông. Dưới đây là phương pháp giải và ví dụ cụ thể giúp bạn hiểu rõ hơn.
Phương pháp giải
- Phương pháp thế: Giải một phương trình để tìm một ẩn và sau đó thay thế vào phương trình còn lại.
- Phương pháp cộng đại số: Cộng hoặc trừ hai phương trình để loại bỏ một ẩn, sau đó giải ẩn còn lại.
Ví dụ
Giải hệ phương trình sau bằng phương pháp thế:
Bước 1: Giải phương trình thứ nhất
Từ phương trình \(x + y = 5\), ta có:
Bước 2: Thay vào phương trình thứ hai
Thay \(y = 5 - x\) vào phương trình thứ hai \(2x - y = 4\):
Ta được:
Bước 3: Tìm \(y\)
Thay \(x = 3\) vào phương trình \(y = 5 - x\):
Kết luận
Vậy nghiệm của hệ phương trình là:
Bài tập tự luyện
- Giải hệ phương trình: \[ \begin{cases} 3x + 2y = 12 \\ 5x - y = 9 \end{cases} \]
- Giải hệ phương trình: \[ \begin{cases} 4x - y = 7 \\ x + 3y = 10 \end{cases} \]

Dạng bài tập Toán - Tìm cực trị của hàm số
Tìm cực trị của hàm số là một dạng bài tập quan trọng trong Giải tích. Dưới đây là phương pháp giải và ví dụ cụ thể giúp bạn hiểu rõ hơn.
Phương pháp tìm cực trị
- Xác định đạo hàm bậc nhất của hàm số: \( f'(x) \).
- Tìm các điểm tới hạn bằng cách giải phương trình \( f'(x) = 0 \).
- Phân tích dấu của \( f'(x) \) trên các khoảng xác định để tìm cực đại và cực tiểu.
Ví dụ
Cho hàm số \( f(x) = x^3 - 3x^2 + 1 \). Hãy tìm các điểm cực trị của hàm số.
Bước 1: Tính đạo hàm bậc nhất
Bước 2: Tìm các điểm tới hạn
Giải phương trình \( f'(x) = 0 \):
Ta được hai nghiệm:
Bước 3: Phân tích dấu của đạo hàm
Xét dấu của \( f'(x) \) trên các khoảng:
- Khoảng \( (-\infty, 0) \): \( f'(x) > 0 \) (hàm số đồng biến)
- Khoảng \( (0, 2) \): \( f'(x) < 0 \) (hàm số nghịch biến)
- Khoảng \( (2, +\infty) \): \( f'(x) > 0 \) (hàm số đồng biến)
Bước 4: Kết luận
Điểm cực đại tại \( x = 0 \) và điểm cực tiểu tại \( x = 2 \).
Bài tập tự luyện
- Cho hàm số \( f(x) = x^4 - 4x^3 + 6x^2 + 1 \). Hãy tìm các điểm cực trị của hàm số.
- Cho hàm số \( f(x) = \sin x - x \). Tìm cực đại và cực tiểu trong khoảng \( [0, 2\pi] \).
Dạng bài tập Toán - Tích phân và ứng dụng của tích phân
Tích phân là một khái niệm quan trọng trong Giải tích, giúp tính toán diện tích dưới đồ thị, thể tích, chiều dài cung và nhiều ứng dụng thực tế khác. Dưới đây là phương pháp giải và ví dụ cụ thể về tích phân cũng như các ứng dụng phổ biến của nó.
Phương pháp tính tích phân
- Xác định hàm số cần tích phân và giới hạn tích phân (nếu có).
- Tính nguyên hàm của hàm số.
- Áp dụng công thức tích phân xác định hoặc tích phân bất định để tính giá trị.
Ví dụ 1: Tính diện tích dưới đồ thị của hàm số
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \( f(x) = x^2 \) và trục hoành, trong khoảng \( [0, 2] \).
Bước 1: Xác định hàm số và giới hạn
Hàm số cần tính tích phân là \( f(x) = x^2 \), với giới hạn từ 0 đến 2.
Bước 2: Tính nguyên hàm
Nguyên hàm của \( x^2 \) là:
Bước 3: Áp dụng tích phân xác định
Tính giá trị của tích phân trong khoảng từ 0 đến 2:
Vậy diện tích hình phẳng là \( \frac{8}{3} \) đơn vị diện tích.
Ví dụ 2: Ứng dụng của tích phân để tính thể tích
Tính thể tích vật thể khi quay quanh trục hoành của vùng phẳng giới hạn bởi hàm số \( f(x) = \sqrt{x} \) trong khoảng \( [0, 4] \).
Bước 1: Xác định hàm số và phương pháp
Sử dụng công thức tính thể tích khi quay quanh trục hoành:
Ở đây, hàm số là \( f(x) = \sqrt{x} \) và khoảng quay là từ 0 đến 4.
Bước 2: Tính tích phân
Tính tích phân của \( [\sqrt{x}]^2 = x \):
Vậy thể tích của vật thể là \( 8\pi \) đơn vị thể tích.
Bài tập tự luyện
- Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \( f(x) = 4 - x^2 \) trong khoảng \( [-2, 2] \).
- Tính thể tích vật thể khi quay quanh trục hoành của vùng phẳng giới hạn bởi hàm số \( f(x) = \sin x \) trong khoảng \( [0, \pi] \).

Dạng bài tập Toán - Hình học không gian - Tính thể tích khối đa diện
Tính thể tích khối đa diện là một dạng bài tập thường gặp trong hình học không gian. Dưới đây là phương pháp tính thể tích và ví dụ cụ thể, giúp bạn hiểu rõ hơn cách giải các bài toán liên quan.
Phương pháp tính thể tích khối đa diện
- Xác định loại khối đa diện (hình lập phương, hình chóp, hình lăng trụ, v.v.).
- Sử dụng công thức tính thể tích tương ứng với từng loại khối.
- Xác định các thông số cần thiết (diện tích đáy, chiều cao, bán kính, v.v.) để thay vào công thức.
Các công thức thường gặp
- Thể tích hình chóp: \[ V = \frac{1}{3} S_{\text{đáy}} \times h \] trong đó \( S_{\text{đáy}} \) là diện tích đáy và \( h \) là chiều cao.
- Thể tích hình lăng trụ: \[ V = S_{\text{đáy}} \times h \]
- Thể tích hình lập phương: \[ V = a^3 \] trong đó \( a \) là độ dài cạnh của hình lập phương.
Ví dụ 1: Tính thể tích hình chóp tam giác đều
Cho hình chóp tam giác đều có diện tích đáy \( S_{\text{đáy}} = 12 \, \text{cm}^2 \) và chiều cao \( h = 9 \, \text{cm} \). Tính thể tích của hình chóp.
Bước 1: Xác định công thức tính thể tích
Sử dụng công thức thể tích hình chóp:
Bước 2: Thay các giá trị vào công thức
Kết luận
Vậy thể tích của hình chóp tam giác đều là \( 36 \, \text{cm}^3 \).
Ví dụ 2: Tính thể tích hình lăng trụ đứng
Cho hình lăng trụ đứng có đáy là hình chữ nhật với chiều dài \( 6 \, \text{cm} \) và chiều rộng \( 4 \, \text{cm} \), chiều cao của hình lăng trụ là \( 10 \, \text{cm} \). Tính thể tích của hình lăng trụ.
Bước 1: Xác định công thức tính thể tích
Sử dụng công thức thể tích hình lăng trụ:
Bước 2: Tính diện tích đáy và thay vào công thức
Diện tích đáy \( S_{\text{đáy}} = 6 \times 4 = 24 \, \text{cm}^2 \).
Thay vào công thức:
Kết luận
Vậy thể tích của hình lăng trụ đứng là \( 240 \, \text{cm}^3 \).
Bài tập tự luyện
- Tính thể tích của một hình lập phương có cạnh dài \( 5 \, \text{cm} \).
- Tính thể tích của hình chóp tứ giác có đáy là hình vuông cạnh \( 4 \, \text{cm} \) và chiều cao \( 6 \, \text{cm} \).
XEM THÊM:
Dạng bài tập Lý - Động lực học chất điểm
Động lực học chất điểm là một phần quan trọng trong Vật lý, giúp chúng ta hiểu rõ hơn về các quy luật chuyển động của vật thể. Dưới đây là một số bài tập cơ bản giúp bạn rèn luyện kỹ năng giải quyết các bài toán liên quan đến động lực học chất điểm.
Bài tập 1: Chuyển động thẳng đều
Cho một chất điểm chuyển động thẳng đều với vận tốc \( v = 5 \, \text{m/s} \). Hãy tính quãng đường mà chất điểm đi được trong khoảng thời gian \( t = 10 \, \text{s} \).
Lời giải:
- Quãng đường \( S \) mà chất điểm đi được trong chuyển động thẳng đều được tính theo công thức: \( S = v \times t \)
- Thay các giá trị vào ta có: \( S = 5 \times 10 = 50 \, \text{m} \)
- Vậy quãng đường mà chất điểm đi được là 50m.
Bài tập 2: Chuyển động thẳng biến đổi đều
Một chất điểm bắt đầu chuyển động với vận tốc ban đầu \( v_0 = 0 \, \text{m/s} \) và gia tốc \( a = 2 \, \text{m/s}^2 \). Hãy tính vận tốc của chất điểm sau thời gian \( t = 5 \, \text{s} \) và quãng đường mà nó đi được trong thời gian đó.
Lời giải:
- Vận tốc của chất điểm sau thời gian \( t \) được tính theo công thức: \( v = v_0 + a \times t \)
- Thay các giá trị vào ta có: \( v = 0 + 2 \times 5 = 10 \, \text{m/s} \)
- Quãng đường đi được tính theo công thức: \( S = v_0 \times t + \frac{1}{2} a \times t^2 \)
- Thay các giá trị vào ta có: \( S = 0 \times 5 + \frac{1}{2} \times 2 \times 5^2 = 25 \, \text{m} \)
- Vậy vận tốc của chất điểm sau 5 giây là 10m/s và quãng đường đi được là 25m.
Bài tập 3: Lực và gia tốc
Một vật có khối lượng \( m = 3 \, \text{kg} \) chịu tác dụng của lực \( F = 9 \, \text{N} \). Hãy tính gia tốc của vật và quãng đường nó đi được sau thời gian 4 giây nếu bắt đầu chuyển động từ trạng thái nghỉ.
Lời giải:
- Gia tốc của vật được tính theo công thức: \( a = \frac{F}{m} \)
- Thay các giá trị vào ta có: \( a = \frac{9}{3} = 3 \, \text{m/s}^2 \)
- Quãng đường đi được tính theo công thức: \( S = \frac{1}{2} a \times t^2 \)
- Thay các giá trị vào ta có: \( S = \frac{1}{2} \times 3 \times 4^2 = 24 \, \text{m} \)
- Vậy gia tốc của vật là 3m/s² và quãng đường đi được sau 4 giây là 24m.
Bài tập 4: Định luật II Newton
Một chiếc xe có khối lượng \( m = 1000 \, \text{kg} \) đang chuyển động với gia tốc \( a = 2 \, \text{m/s}^2 \). Hãy tính lực kéo của động cơ xe.
Lời giải:
- Lực kéo của động cơ được tính theo công thức: \( F = m \times a \)
- Thay các giá trị vào ta có: \( F = 1000 \times 2 = 2000 \, \text{N} \)
- Vậy lực kéo của động cơ xe là 2000N.
Bài tập 5: Định luật bảo toàn động lượng
Một viên bi có khối lượng \( m_1 = 0,5 \, \text{kg} \) đang chuyển động với vận tốc \( v_1 = 4 \, \text{m/s} \) thì va chạm đàn hồi với một viên bi khác có khối lượng \( m_2 = 1 \, \text{kg} \) đang đứng yên. Hãy tính vận tốc của hai viên bi sau va chạm.
Lời giải:
- Sử dụng định luật bảo toàn động lượng: \( m_1 v_1 + m_2 v_2 = m_1 v'_1 + m_2 v'_2 \)
- Do va chạm đàn hồi, năng lượng cũng được bảo toàn:
- Sử dụng hai phương trình bảo toàn động lượng và năng lượng để tính toán \( v'_1 \) và \( v'_2 \).
- Sau khi giải hệ phương trình, ta có:
- Vận tốc của viên bi 1 sau va chạm: \( v'_1 = \frac{m_1 - m_2}{m_1 + m_2} \times v_1 = -\frac{1}{3} \times 4 = -\frac{4}{3} \, \text{m/s} \)
- Vận tốc của viên bi 2 sau va chạm: \( v'_2 = \frac{2m_1}{m_1 + m_2} \times v_1 = \frac{4}{3} \, \text{m/s} \)
- Vậy sau va chạm, vận tốc của viên bi 1 là \(-\frac{4}{3} \, \text{m/s}\) và vận tốc của viên bi 2 là \(\frac{4}{3} \, \text{m/s}\).

Dạng bài tập Lý - Dòng điện trong các mạch điện
Trong phần này, chúng ta sẽ đi sâu vào việc giải quyết các bài tập liên quan đến dòng điện trong các mạch điện, một chủ đề cơ bản nhưng quan trọng trong vật lý.
-
Bài tập 1: Mạch điện nối tiếp
Cho mạch điện gồm ba điện trở \(R_1\), \(R_2\) và \(R_3\) được mắc nối tiếp với nhau. Hiệu điện thế tổng cộng của mạch là \(U\). Tính dòng điện \(I\) trong mạch và hiệu điện thế trên từng điện trở.
Giải:
- Tổng điện trở: \(R = R_1 + R_2 + R_3\)
- Dòng điện trong mạch: \(I = \frac{U}{R}\)
- Hiệu điện thế trên mỗi điện trở:
- \(U_1 = I \cdot R_1\)
- \(U_2 = I \cdot R_2\)
- \(U_3 = I \cdot R_3\)
-
Bài tập 2: Mạch điện song song
Một mạch điện gồm hai điện trở \(R_1\) và \(R_2\) được mắc song song, hiệu điện thế giữa hai đầu mạch là \(U\). Tính dòng điện qua từng điện trở và tổng dòng điện trong mạch.
Giải:
- Dòng điện qua từng điện trở:
- \(I_1 = \frac{U}{R_1}\)
- \(I_2 = \frac{U}{R_2}\)
- Tổng dòng điện: \(I = I_1 + I_2\)
- Dòng điện qua từng điện trở:
-
Bài tập 3: Mạch hỗn hợp
Cho mạch điện gồm ba điện trở, trong đó \(R_1\) nối tiếp với nhánh song song của \(R_2\) và \(R_3\). Hiệu điện thế giữa hai đầu mạch là \(U\). Tính dòng điện qua mạch và hiệu điện thế trên từng điện trở.
Giải:
- Điện trở tương đương của nhánh song song: \[R_{song\_song} = \frac{R_2 \cdot R_3}{R_2 + R_3}\]
- Tổng điện trở của mạch: \[R_{total} = R_1 + R_{song\_song}\]
- Dòng điện qua mạch: \[I = \frac{U}{R_{total}}\]
- Hiệu điện thế trên \(R_1\): \[U_1 = I \cdot R_1\]
- Hiệu điện thế trên nhánh song song: \[U_{song\_song} = U - U_1\]
- Dòng điện qua \(R_2\) và \(R_3\):
- \(I_2 = \frac{U_{song\_song}}{R_2}\)
- \(I_3 = \frac{U_{song\_song}}{R_3}\)

Dạng bài tập Lý - Định luật bảo toàn năng lượng
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản và quan trọng nhất trong vật lý. Nó phát biểu rằng trong một hệ kín, năng lượng không thể tự sinh ra hay mất đi mà chỉ có thể chuyển đổi từ dạng này sang dạng khác. Điều này có nghĩa là tổng năng lượng của hệ luôn luôn không đổi.
Dưới đây là một số dạng bài tập phổ biến về định luật bảo toàn năng lượng mà học sinh thường gặp trong các kỳ thi:
- Bài tập về con lắc đơn:
Khi một con lắc đơn dao động, năng lượng của nó luân phiên giữa thế năng và động năng. Ở vị trí cao nhất, con lắc có thế năng cực đại và động năng bằng 0. Khi con lắc đi qua vị trí cân bằng, thế năng giảm về 0 và động năng đạt cực đại. Việc áp dụng định luật bảo toàn năng lượng giúp tính toán các giá trị này một cách chính xác.
Ví dụ: Xác định vận tốc của con lắc tại vị trí thấp nhất khi biết độ cao ban đầu của nó là \(h\).
Lời giải: Sử dụng định luật bảo toàn năng lượng:
\[ mgh = \frac{1}{2}mv^2 \Rightarrow v = \sqrt{2gh} \] - Bài tập về chất điểm rơi tự do:
Đối với bài tập này, chất điểm ban đầu có thế năng khi ở độ cao \(h\) và khi rơi tự do, thế năng này sẽ chuyển hóa thành động năng.
Ví dụ: Tính vận tốc của một vật khi chạm đất nếu nó rơi từ độ cao \(h = 20m\).
Lời giải: Sử dụng định luật bảo toàn năng lượng:
\[ mgh = \frac{1}{2}mv^2 \Rightarrow v = \sqrt{2gh} \] - Bài tập về mạch điện:
Trong các bài tập về mạch điện, định luật bảo toàn năng lượng thường được áp dụng để tính toán công suất, năng lượng tiêu thụ của các thiết bị trong mạch.
Ví dụ: Tính năng lượng tiêu thụ của một bóng đèn trong 2 giờ nếu công suất của nó là 60W.
Lời giải: Sử dụng công thức:
\[ W = P \times t = 60W \times 2h = 120Wh \]
Việc luyện tập các dạng bài tập này không chỉ giúp củng cố kiến thức lý thuyết mà còn nâng cao khả năng vận dụng linh hoạt định luật bảo toàn năng lượng trong các tình huống khác nhau.
Dạng bài tập Tiếng Anh - Cấu trúc câu điều kiện
Câu điều kiện trong tiếng Anh là một cấu trúc ngữ pháp quan trọng giúp diễn đạt những tình huống có thể xảy ra, không thể xảy ra, hoặc đã xảy ra trong quá khứ. Có ba loại câu điều kiện cơ bản:
-
Câu điều kiện loại 1 (First Conditional)
Câu điều kiện loại 1 dùng để diễn đạt một tình huống có thể xảy ra trong tương lai nếu điều kiện được đáp ứng.
- Cấu trúc:
If + S + V (hiện tại đơn), S + will + V (nguyên mẫu) - Ví dụ:
If it rains, we will cancel the match. (Nếu trời mưa, chúng ta sẽ hủy trận đấu.)
- Cấu trúc:
-
Câu điều kiện loại 2 (Second Conditional)
Câu điều kiện loại 2 dùng để diễn đạt một tình huống không thực tế hoặc khó xảy ra ở hiện tại hoặc tương lai.
- Cấu trúc:
If + S + V (quá khứ đơn), S + would + V (nguyên mẫu) - Ví dụ:
If I were you, I would study harder. (Nếu tôi là bạn, tôi sẽ học chăm chỉ hơn.)
- Cấu trúc:
-
Câu điều kiện loại 3 (Third Conditional)
Câu điều kiện loại 3 dùng để diễn đạt một tình huống không có thật trong quá khứ, và kết quả của nó cũng không có thật.
- Cấu trúc:
If + S + had + V3, S + would have + V3 - Ví dụ:
If he had trained harder, he would have won the match. (Nếu anh ấy đã tập luyện chăm chỉ hơn, anh ấy đã thắng trận đấu.)
- Cấu trúc:
Lưu ý: Trong câu điều kiện loại 2 và 3, động từ "to be" luôn chia là "were" đối với tất cả các ngôi trong mệnh đề điều kiện.
Bạn có thể thực hành bằng cách viết các câu với các tình huống khác nhau để hiểu rõ hơn cách sử dụng câu điều kiện trong tiếng Anh.

Dạng bài tập Tiếng Anh - Sử dụng thì quá khứ hoàn thành
Thì quá khứ hoàn thành (Past Perfect Tense) là một trong những thì quan trọng trong tiếng Anh, thường được sử dụng để diễn tả một hành động đã hoàn thành trước một thời điểm hoặc một hành động khác trong quá khứ.
Dưới đây là các bước hướng dẫn và ví dụ để giúp bạn làm quen và thành thạo với thì này:
-
Cấu trúc thì quá khứ hoàn thành:
- Khẳng định:
S + had + V(p.p) + O - Phủ định:
S + had not (hadn't) + V(p.p) + O - Nghi vấn:
Had + S + V(p.p) + O?
- Khẳng định:
-
Cách sử dụng thì quá khứ hoàn thành:
- Diễn tả một hành động đã hoàn thành trước một hành động khác trong quá khứ.
- Diễn tả một hành động đã hoàn thành trước một thời điểm cụ thể trong quá khứ.
Ví dụ:
- By the time the train arrived, she had left the station.
- They had finished their homework before the movie started.
-
Nhận biết thì quá khứ hoàn thành:
- Thường đi kèm với các từ như before, after, by the time, already, và until then.
- Các hành động trong câu có sự liên kết chặt chẽ về mặt thời gian, với một hành động xảy ra trước hành động kia.
-
Bài tập thực hành:
- Hoàn thành câu bằng thì quá khứ hoàn thành:
By the time we arrived, they___ (finish)their dinner.
Answer:had finished - Viết lại câu sử dụng thì quá khứ hoàn thành:
She left the office. I arrived.
Answer:By the time I arrived, she had left the office.
- Hoàn thành câu bằng thì quá khứ hoàn thành:
Qua các bài tập trên, bạn sẽ hiểu rõ hơn về cách sử dụng thì quá khứ hoàn thành trong tiếng Anh. Hãy tiếp tục luyện tập để nắm vững và sử dụng thành thạo thì này trong giao tiếp và viết văn bản.
Dạng bài tập Tiếng Anh - Bài tập ngữ pháp về câu bị động
Câu bị động là một phần quan trọng trong ngữ pháp tiếng Anh, được sử dụng để nhấn mạnh đối tượng nhận hành động thay vì người thực hiện hành động. Dưới đây là hướng dẫn cơ bản và một số bài tập giúp bạn làm quen và thực hành cấu trúc này.
1. Cấu trúc cơ bản của câu bị động
Câu bị động được hình thành từ cấu trúc:
- Thì hiện tại đơn: am/is/are + V3/ed
- Thì quá khứ đơn: was/were + V3/ed
- Thì tương lai đơn: will be + V3/ed
- Thì hiện tại hoàn thành: have/has been + V3/ed
2. Cách chuyển từ câu chủ động sang câu bị động
- Xác định tân ngữ (object) trong câu chủ động.
- Đưa tân ngữ lên làm chủ ngữ (subject) trong câu bị động.
- Sử dụng động từ "to be" phù hợp với thì của câu chủ động.
- Động từ chính của câu được chuyển sang dạng quá khứ phân từ (V3/ed).
- Nếu cần, thêm "by" theo sau bởi chủ ngữ của câu chủ động.
3. Bài tập thực hành
Bài tập 1: Chuyển các câu sau sang dạng bị động
- They deliver the mail every day.
- The teacher explains the lesson clearly.
- People speak English in many countries.
- The company has launched a new product.
Bài tập 2: Hoàn thành câu bị động dựa trên từ cho sẵn
- The letter _____ (send) yesterday.
- The cake _____ (bake) by Mary.
- The room _____ (clean) right now.
- The report _____ (finish) by the team.
Đáp án:
- Bài tập 1:
- The mail is delivered every day.
- The lesson is explained clearly by the teacher.
- English is spoken in many countries.
- A new product has been launched by the company.
- Bài tập 2:
- The letter was sent yesterday.
- The cake was baked by Mary.
- The room is being cleaned right now.
- The report has been finished by the team.