Tính thể tích của 5 khối đa diện đều – Tài liệu chính thức từ Vted

Trong bài viết này, chúng tôi sẽ giới thiệu công thức tính thể tích của 5 khối đa diện đều: tứ diện đều, hình lập phương, bát diện đều, hình 12 mặt đều và hình 20 mặt đều từ khoá học PRO X TOÁN 2018 tại Vted. Bạn có thể tham khảo bài giảng và bài tập đi kèm tại đây.

Bạn đang xem: Tính thể tích của 5 khối đa diện đều – Tài liệu chính thức từ Vted

Tứ diện đều

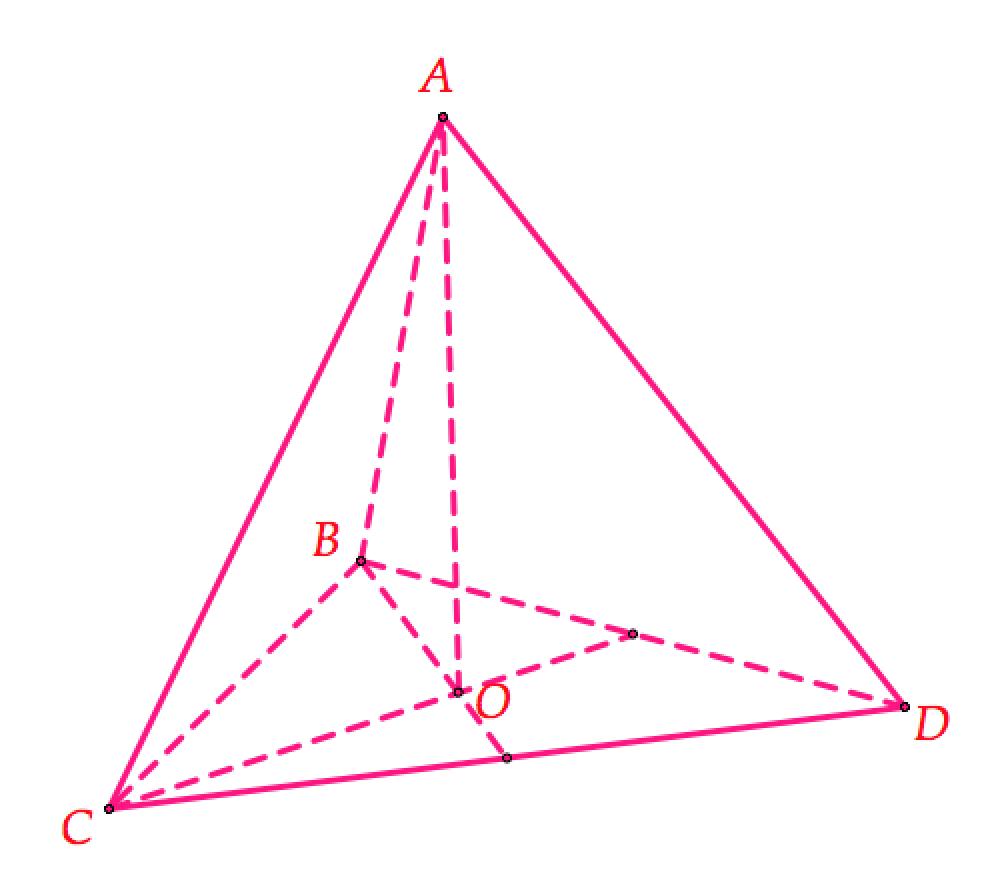
1. Tứ diện đều $ABCD$ có cạnh $a$.
   • Diện tích mặt đáy: $S=frac{{a^2sqrt{3}}}{4}$
   • Chiều cao: $h=AO=sqrt{A{{B}^{2}}-O{{B}^{2}}}= frac{{asqrt{6}}}{3}$
   • Thể tích: $V=frac{1}{3}Sh=frac{{a^3sqrt{2}}}{12}.

Hình lập phương

2. Hình lập phương có cạnh $a$.
   • Thể tích: $V=a^3$.

Bát diện đều

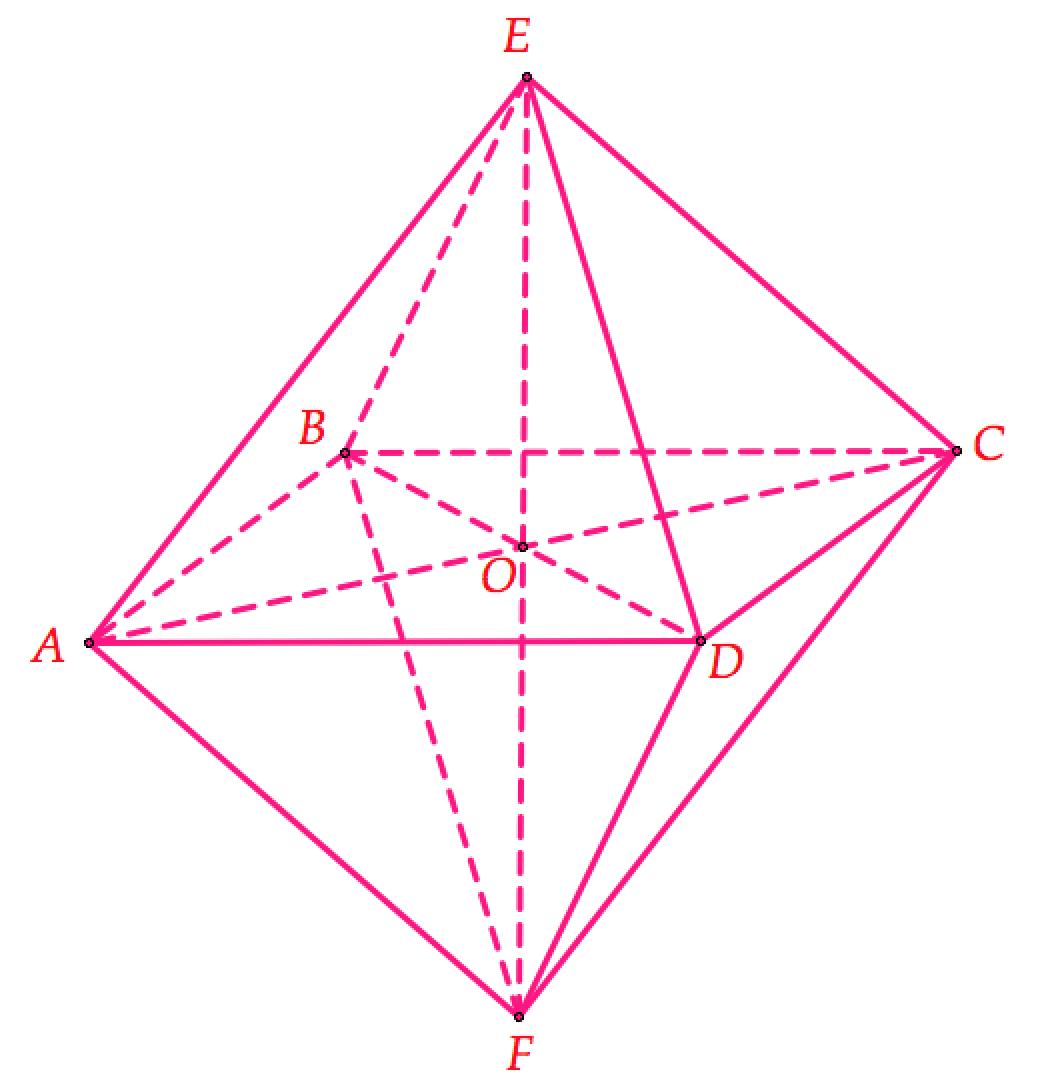
3. Bát diện đều $ABCDEF$ có cạnh $a$.
   • Diện tích mặt đáy: $S_{ABCD} = {a^2}$
   • Chiều cao: $EF=2EO=2sqrt{B{{E}^{2}}-B{{O}^{2}}}=asqrt{2}$
   • Thể tích: $V=frac{1}{3}{{S}_{ABCD}}.EF=frac{1}{3}.{{a}^{2}}.asqrt{2}=frac{{a^3sqrt{2}}}{3}.

Hình 12 mặt đều

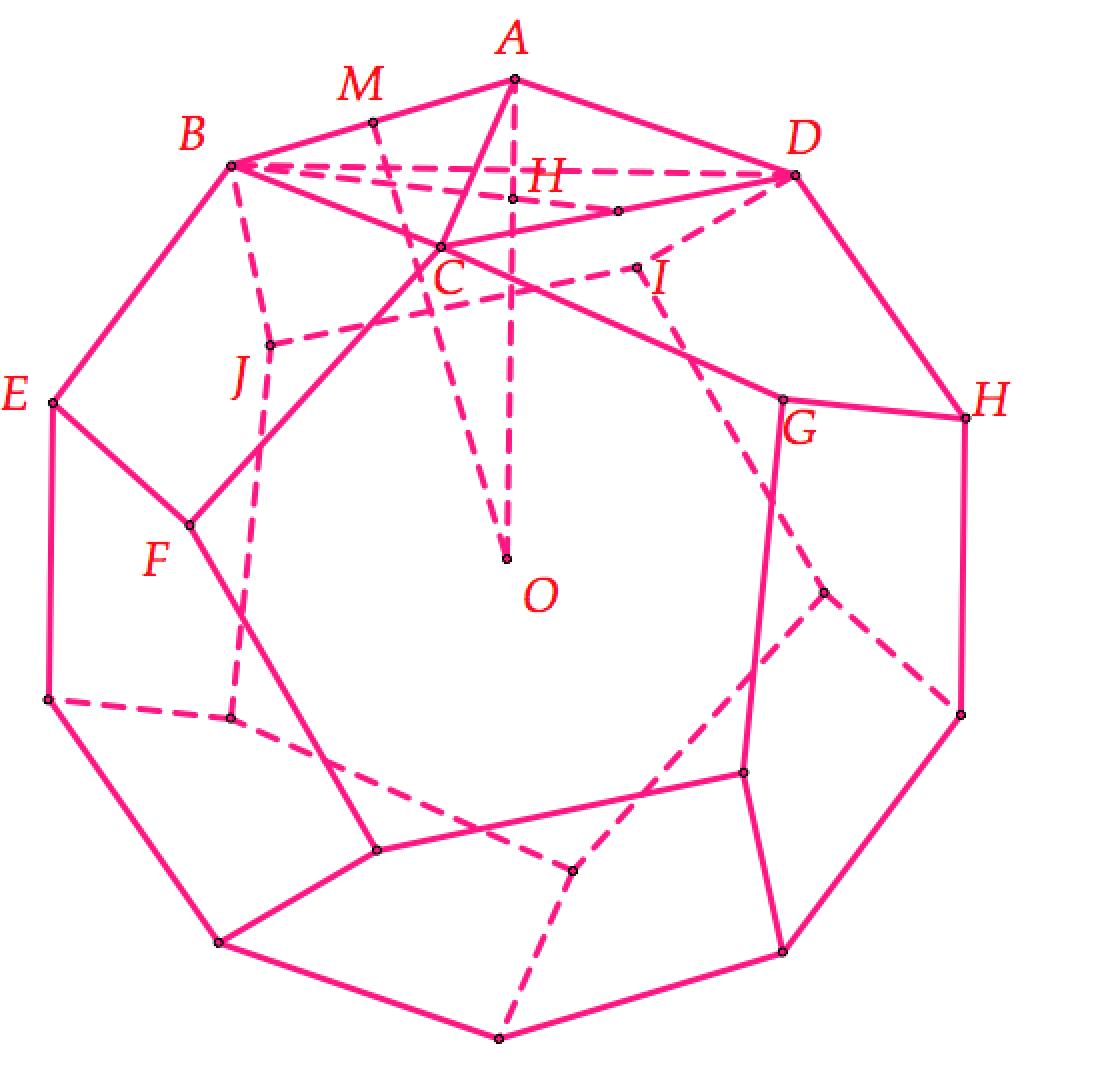
4. Hình 12 mặt đều có cạnh $a$.
   • Tìm bán kính: $OA= frac{A{{B}^{2}}}{2AH}= frac{{asqrt{3}}}{sqrt{5}-1}$
   • Thể tích: $V=frac{{{a}^{3}}(15+7sqrt{5})}{4}$.

Xem thêm : Cách Hàn Mạch Điện Tử: Hướng Dẫn Chi Tiết và Đơn Giản

Chú ý: Bán kính mặt cầu ngoại tiếp khối đa diện có thể tính nhanh chóng bằng công thức $R= frac{A{{B}^{2}}}{2sqrt{A{{B}^{2}}-R_{BCD}^{2}}}.$

Hình 20 mặt đều

5. Hình 20 mặt đều có cạnh $a$.
   • Thể tích: $V=frac{5(3+sqrt{5}){{a}^{3}}}{12}$.

Chú ý: Khối 12 mặt đều và khối 20 mặt đều chỉ để tham khảo; không nên sử dụng cho các bài toán thực tế.

Nếu bạn muốn biết thêm chi tiết về 5 khối đa diện đều, hãy xem tại đây.

Lợi ích của việc học toán tại Vted

Gói Combo X 2020 của Vted cung cấp 4 khoá học luyện thi duy nhất và đầy đủ nhất cho các đối tượng thí sinh:

1. PRO X 2020: Luyện thi THPT Quốc Gia 2020.
2. PRO XMAX 2020: Luyện nâng cao 9 đến 10 chỉ dành cho học sinh giỏi.
3. PRO XPLUS 2020: Luyện đề thi tham khảo THPT Quốc Gia 2020 môn Toán.
4. PRO XMIN 2020: Luyện đề thi tham khảo THPT Quốc Gia 2020 môn Toán từ các trường THPT Chuyên và Sở giáo dục đào tạo.

Quý thầy cô giáo, quý phụ huynh và các em học sinh có thể mua Combo gồm cả 4 khoá học cùng lúc hoặc chọn từng khoá học phù hợp với nhu cầu và năng lực bản thân.

Tại sao nên học toán tại Vted?

Có 6 lý do tạo nên sự khác biệt của các khoá học môn Toán tại Vted của thầy Đặng Thành Nam:

• Nội dung chất lượng luôn đi sát với thực tiễn đề thi.
• Học 1 được 3 và còn hơn thế nữa với tổng thời lượng lên tới 500 giờ/khoá.
• Tài liệu hỗ trợ và bài tập đi kèm đầy đủ, chỉ sợ học viên phát hoảng vì quá nhiều.
• Giao lưu trực tuyến hàng tuần và có thể gặp trực tiếp tại Hà Nội.
• Học phí hợp lý và liên tục cập nhật các nội dung mới hoàn toàn miễn phí.
• Đảm bảo kết quả thi nếu học viên nắm vững 70% kiến thức từ khoá học.

Hãy từ chối những lời mời mọc của những thành phần không trung thực và thông báo cho chúng tôi nếu bạn gặp phải hành vi lừa đảo. Chúng tôi sẽ giữ bí mật và hỗ trợ bạn trong việc xử lý những tình huống này.

Xem nhận xét của học viên về các khoá học tại Vted tại đây.

Hãy truy cập Vted.vn để trải nghiệm việc học toán online chất lượng cao!

Nguồn: https://cite.edu.vn
Danh mục: Học tập