I. Mạch Cộng
1. Mạch cộng nửa
Để đơn giản, ta xét mạch cộng nhị phân 1 bit. Khi xét 4 trạng thái logic của số A và số B, ta có kết quả như sau:
- Ngõ ra S và C: S = AB + AB và C = AB
- S là ngõ ra của cổng EXOR 2 ngõ vào A và B; C là ngõ ra của cổng AND.
Cấu trúc logic của mạch cộng nửa (haft adder) sẽ như sau:
Bạn đang xem: Nguyên lý mạch logic số học
2. Mạch cộng đủ
Sau khi thực hiện phép cộng lần đầu, kết quả là S0 và số nhớ C0. Nếu tiếp tục cộng lần 2 với trạng thái logic thay đổi của A và B, S sẽ không chỉ là tổng của A và B mà còn gồm cả C0 trước đó. Khi đó, ta có mạch cộng đủ (full adder).
Cấu trúc của mạch cộng đủ sẽ là:
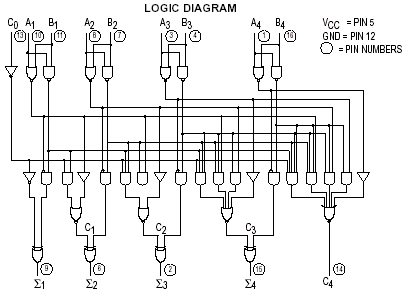
3. Cộng nhiều bit
a) Cộng song song
Khi cộng 2 số có nhiều bit hơn, ta có thể cộng 2 bit LSB trước để có bit tổng (LSB). Số nhớ sẽ được đưa tới để cộng với 2 bit kế tiếp và tạo ra bit tổng ở các hàng kế tiếp. Phép cộng cuối cùng giữa 2 bit MSB sẽ tạo ra bit tổng ở hàng đó, và số nhớ sẽ trở thành bit LSB của tổng.
Ví dụ về mạch cộng nhiều bit (4 bit) như sau:
b) Cộng nối tiếp
Ngoài cách cộng song song, ta còn có mạch cộng nối tiếp. Khi này, 2 bit LSB của các số được cộng trước sẽ chuyển tới một bộ dịch, và số nhớ sẽ quay trở về để cộng với 2 bit kế tiếp. Quá trình này diễn ra cho đến khi thực hiện phép cộng cuối cùng giữa 2 bit cuối cùng để có bit tổng ở đó. Số nhớ khi này trở thành bit LSB của tổng.
Mạch cộng nối tiếp cho phép cung cấp sẵn các bit nhớ để phục vụ cho các phép cộng ở các hàng được thực hiện cùng một lúc.
Ví dụ về mạch cộng nối tiếp 4 bit như sau:
.png)
II. Mạch Trừ
1. Mạch trừ nửa và trừ đủ
Mạch trừ cũng gồm 2 loại mạch tương tự như mạch cộng, đó là mạch trừ nửa (haft subtractor) và trừ đủ (full subtractor). Mạch trừ thực chất là phép cộng với số âm. Để có số âm của một số, ta lấy bù 1 của số đó (đảo các bit). Khi thực hiện mạch, đó là cổng đảo.
Cấu trúc của mạch trừ nửa sẽ như sau:

Cấu trúc của mạch trừ đủ sẽ như sau:

2. Mạch trừ nhiều bit
Với mạch trừ nhị phân nhiều bit, ta có thể thực hiện cộng trừ từng bit riêng lẻ. Bit của số bị trừ cần được đảo, và số nhớ của tầng cuối cần đem về bit nhớ ban đầu của tầng đầu. Dưới đây là các minh hoạ mạch trừ nhị phân 4 bit.


3. Mạch cộng trừ kết hợp
Bằng cách thêm vào một số cổng logic cần thiết, ta có thể tạo ra mạch có thể cộng hoặc trừ tuỳ theo ngõ vào điều khiển CT. Khi CT = 0, các cổng EXOR có một ngõ vào ở mức thấp, cho phép số B qua mà không bị đảo. Khi CT = 1, các cổng EXOR có một ngõ vào ở mức cao, hoạt động như một cổng NOT, số B sẽ bị đảo. Khi này, mạch thực hiện phép cộng A + (-B) (tức là phép trừ).
Co3 là bit LSB của tổng, được đưa qua cổng AND để trở về Ci0, cho phép cộng nhiều bit.

Ngoài cách dùng bù 1, ta cũng có thể dùng bù 2 (lấy bù 1 rồi cộng thêm 1) để thực hiện phép toán trừ nhị phân, kể cả số có dấu. Cách này được sử dụng phổ biến trong VXL và máy tính.
III. Cộng Trừ BCD
1. Cộng 2 số BCD
Cộng 2 số BCD tương tự như cộng các số nhị phân. Khi tổng vượt quá 1001, tức là không còn là số BCD nữa, ta cộng tổng với 0110 để có một số BCD mới và số nhớ sẽ là hàng chục của tổng.
Ví dụ về mạch cộng 2 số BCD 1 bit như sau:

2. Trừ 2 số BCD
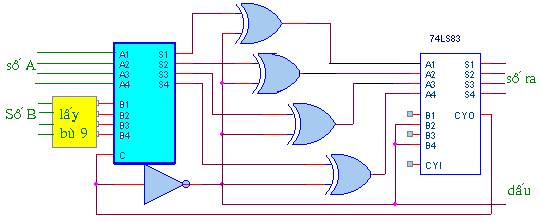
Để thực hiện phép trừ BCD, ta lấy bù 9 của số trừ và thực hiện phép cộng với số bị trừ. Lấy bù 9 của một số tức là lấy 9 trừ đi số đó.
Ví dụ về phép trừ BCD:


IV. Mạch Nhân Chia
1. Mạch nhân 2 số nhị phân
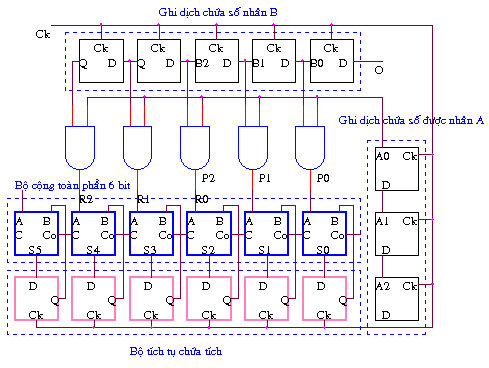
Nguyên tắc của phép nhân 2 số nhị phân là phép cộng nhiều lần. Mạch nhân 2 số nhị phân được thực hiện bằng cách thực hiện các phép cộng liên tiếp. Cấu trúc của mạch bao gồm các bộ dịch để chứa số được nhân, các bộ cộng toàn phần để tính toán kết quả cuối cùng và số nhớ tương ứng.
Ví dụ về mạch nhân 2 số nhị phân 4 bit như sau:

2. Mạch chia 2 số nhị phân
Mạch chia 2 số nhị phân thực hiện các phép trừ liên tiếp để tìm kết quả. Dưới đây là các mạch thực hiện phép chia nhị phân, nhưng do phức tạp nên không được trình bày chi tiết ở đây.
V. Bộ Logic và Số Học
ALU (Arithmetic Logic Unit) là thành phần quan trọng của CPU trong máy tính, có thể thực hiện nhiều phép tính số học và logic dựa trên dữ liệu. ALU thường bao gồm các phép cộng, trừ, AND, OR, XOR, dịch chuyển, tăng giảm dần và cả phép nhân, chia.
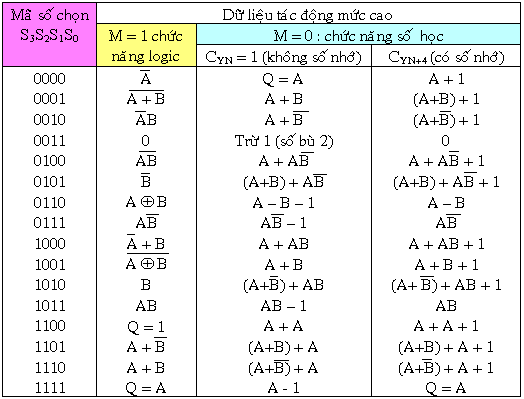
Hình ảnh dưới đây là hình ảnh khối của ALU 74LS181 và bảng hoạt động:

Ngoài ra, còn có mạch ALU 74LS382, cũng là mạch 4 bit nhưng có ít chức năng hơn 74LS181. Mạch này có tính năng báo tràn (overflow) khi số kết quả vượt quá giới hạn của số 4 bit.

Nguồn: https://cite.edu.vn
Danh mục: Học tập